Enhanced Pulse Compression within Sign-Alternating Dispersion Waveguides
Abstract
:1. Introduction
2. Concept of Alternating Dispersion Waveguides and Methods
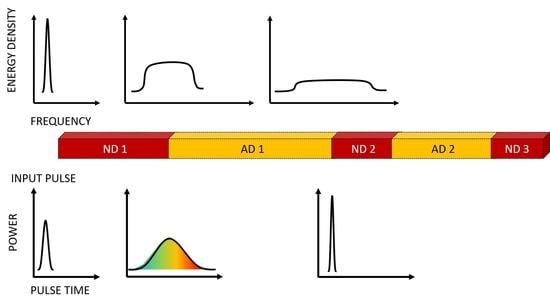
2.1. Concept of Alternating Dispersion Waveguides
2.2. Methods
3. Results
3.1. Convergence to Near Parabolic Spectral Phase in the SPM-Dominated Regime
3.1.1. SPM Effects on Second-Order Spectral Phase
3.1.2. SPM Effects on Third-Order and Higher Spectral Phase
3.1.3. SPM Leads to a Parabolic Spectral Phase Convergence
3.1.4. Impact of SPM Induced Phase Coefficient Reduction in the Design and Context of Alternating Dispersion Waveguides
3.2. AD GVD in the Dispersion-Dominated Regime
3.3. Sign-Alternating Dispersion in Integrated Photonics
4. Discussion
- The minimal compressed duration is the duration of the fundamental soliton allowed with a given pulse energy because spectral generation terminates once a soliton is formed, and the fundamental soliton is the shortest allowed.
- The final pulse duration may not reach the lower limit duration described in 1., since formation of a higher-order soliton, at a narrower bandwidth stops nonlinear compression to the fundamental. The higher-order soliton forms first because its generation length is shorter by a factor of the soliton number than that of the fundamental soliton [1,40].
5. Conclusions
Supplementary Materials
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Dudley, J.M.; Genty, G.; Coen, S. Supercontinuum generation in photonic crystal fiber. Rev. Mod. Phys. 2006, 78, 1135–1184. [Google Scholar] [CrossRef]
- Heidt, A.M.; Feehan, J.S.; Price, J.H.V.; Feurer, T. Limits of coherent supercontinuum generation in normal dispersion fibers. J. Opt. Soc. Am. B 2017, 34, 764–775. [Google Scholar] [CrossRef] [Green Version]
- Manzoni, C.; Mücke, O.D.; Cirmi, G.; Fang, S.; Moses, J.; Huang, S.-W.; Hong, K.-H.; Cerullo, G.; Kärtner, F.X. Coherent pulse synthesis: Towards sub-cycle optical waveforms. Laser Photonics Rev. 2015, 9, 129–171. [Google Scholar] [CrossRef] [Green Version]
- Hassan, M.T.; Luu, T.T.; Moulet, A.; Raskazovskaya, O.; Zhokhov, P.; Garg, M.; Karpowicz, N.; Zheltikov, A.M.; Pervak, V.; Krausz, F.; et al. Optical attosecond pulses and tracking the nonlinear response of bound electrons. Nature 2016, 530, 66–70. [Google Scholar] [CrossRef] [PubMed]
- Hemmer, M.; Baudisch, M.; Thai, A.; Couairon, A.; Biegert, J. Self-compression to sub-3-cycle duration of mid-infrared optical pulses in dielectrics. Opt. Express 2013, 21, 28095–28102. [Google Scholar] [CrossRef] [Green Version]
- Chen, H.-W.; Zia, H.; Lim, J.K.; Xu, S.; Yang, Z.; Kärtner, F.X.; Chang, G. 3 GHz, Yb-fiber laser-based, few-cycle ultrafast source at the Ti: Sapphire laser wavelength. Opt. Lett. 2013, 38, 4927–4930. [Google Scholar] [CrossRef]
- Yu, M.; Okawachi, Y.; Griffith, A.G.; Picqué, N.; Lipson, M.; Gaeta, A.L. Silicon-chip-based mid-infrared dual-comb spectroscopy. Nat. Commun. 2018, 9, 1–6. [Google Scholar] [CrossRef] [Green Version]
- Luke, K.; Okawachi, Y.; Lamont, M.R.E.; Gaeta, A.L.; Lipson, M. Broadband mid-infrared frequency comb generation in a Si3N4 microresonator. Opt. Lett. 2015, 40, 4823. [Google Scholar] [CrossRef]
- Schliesser, A.; Picqué, N.; Hänsch, T.W. Mid-infrared frequency combs. Nat. Photonics 2012, 6, 40–449. [Google Scholar] [CrossRef] [Green Version]
- Rieker, G.B.; Giorgetta, F.R.; Swann, W.C.; Kofler, J.; Zolot, A.M.; Sinclair, L.C.; Baumann, E.; Cromer, C.; Petron, G.; Sweeney, C.; et al. Frequency-comb-based remote sensing of greenhouse gases over kilometer air paths. Optica 2014, 1, 290. [Google Scholar] [CrossRef] [Green Version]
- Holzwarth, R. Optical frequency metrology. Nat. Rev. 2002, 416, 1–5. [Google Scholar]
- Humbert, G.; Wadsworth, W.J.; Leon-Saval, S.G.; Knight, J.C.; Birks, T.A.; Russell, P.S.J.; Lederer, M.J.; Kopf, D.; Wiesauer, K.; Breuer, E.I.; et al. Supercontinuum generation system for optical coherence tomography based on tapered photonic crystal fibre. Opt. Express 2006, 14, 1596. [Google Scholar] [CrossRef]
- Unterhuber, A.; Považay, B.; Bizheva, K.; Hermann, B.; Sattmann, H.; Stingl, A.; Le, T.; Seefeld, M.; Menzel, R.; Preusser, M. Advances in broad bandwidth light sources for ultrahigh resolution optical coherence tomography. Phys. Med. Biol. 2004, 49, 1235–1246. [Google Scholar] [CrossRef]
- Israelsen, N.M.; Petersen, C.R.; Barh, A.; Jain, D.; Jensen, M.; Hannesschlaeger, G.; Tidemand-Lichtenberg, P.; Pedersen, C.; Podoleanu, A.; Bang, O.L. Real-time high-resolution mid-infrared optical coherence tomography. Light Sci. Appl. 2019, 8, 1–13. [Google Scholar] [CrossRef] [Green Version]
- Du, Q.; Luo, Z.; Zhong, H.; Zhang, Y.; Huang, Y.; Du, T.; Zhang, W.; Gu, T.; Hu, J. Chip-scale broadband spectroscopic chemical sensing using an integrated supercontinuum source in a chalcogenide glass waveguide. Photonics Res. 2018, 6, 506–510. [Google Scholar] [CrossRef]
- Kaminski, C.F.; Watt, R.S.; Elder, A.D.; Frank, J.H.; Hult, J. Supercontinuum radiation for applications in chemical sensing and microscopy. Appl. Phys. B 2008, 92, 367–378. [Google Scholar] [CrossRef]
- Zia, H.; Lüpken, N.M.; Hellwig, T.; Fallnich, C.; Boller, K.-J. Supercontinuum Generation in Media with Sign-Alternated Dispersion. Laser Photonics Rev. 2020, 6, 2000031. [Google Scholar] [CrossRef]
- Carlson, D.R.; Hutchison, P.; Hickstein, D.D.; Papp, S.B. Generating few-cycle pulses with integrated nonlinear photonics. Opt. Express 2019, 27, 37374–37382. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Foster, M.A.; Gaeta, A.L.; Cao, Q.; Trebino, R. Soliton-effect compression of supercontinuum to few-cycle durations in photonic nanowires. Opt. Express 2005, 13, 6848–6855. [Google Scholar] [CrossRef] [PubMed]
- Singh, N.; Vermulen, D.; Ruocco, A.; Li, N.; Ippen, E.; Kärtner, F.X.; Watts, M.R. Supercontinuum generation in varying dispersion and birefringent silicon waveguide. Opt. Express 2019, 27, 31698–31712. [Google Scholar] [CrossRef] [Green Version]
- Ciret, C.; Gorza, S.P. Generation of ultra-broadband coherent supercontinua in tapered and dispersion-managed silicon nanophotonic waveguides. JOSA B 2017, 34, 1156–1162. [Google Scholar] [CrossRef] [Green Version]
- Hu, H.; Zhang, X.; Li, W.; Dutta, N.K. Simulation of octave spanning mid-infrared supercontinuum generation in dispersion-varying planar waveguides. Appl. Opt. 2015, 54, 3448–3454. [Google Scholar] [CrossRef]
- Travers, J.C.; Popov, S.V.; Taylor, J.R. Extended blue supercontinuum generation in cascaded holey fibers. Opt. Lett. 2005, 30, 3132–3134. [Google Scholar] [CrossRef]
- Alfano, R.R. The Supercontinuum Laser Source: The Ultimate White Light; Springer: New York, NY, USA, 2016. [Google Scholar]
- Zeytunyan, A.; Yesayan, G.; Mouradian, L.; Kockaert, P.; Emplit, P.; Louradour, F.; Barthélémy, A. Nonlinear-dispersive similariton of passive fiber. J. Eur. Opt. Soc. Rapid Publ. 2009, 4. [Google Scholar] [CrossRef] [Green Version]
- Finot, C.; Millot, G.; Dudley, J.M. Asymptotic characteristics of parabolic similariton pulses in optical fiber amplifiers. Opt. Lett. 2004, 29, 2533–2535. [Google Scholar] [CrossRef]
- Finot, C.; Parmigiani, F.; Petropoulos, P.; Richardson, D.J. Parabolic pulse evolution in normally dispersive fiber amplifiers preceding the similariton formation regime. Opt. Express 2006, 14, 3161–3170. [Google Scholar] [CrossRef] [PubMed]
- Finot, C. Dispersion managed self-similar parabolic pulses. J. Opt. 2008, 10, 085101. [Google Scholar] [CrossRef] [Green Version]
- Hori, T.; Takayanagi, J.; Nishizawa, N.; Goto, T. Flatly broadened, wideband and low noise supercontinuum generation in highly nonlinear hybrid fiber. Opt. Express 2004, 12, 317–324. [Google Scholar] [CrossRef]
- Heidt, A.M.; Rothhardt, J.; Hartung, A.; Bartelt, H.; Rohwer, E.G.; Limpert, J.; Tünnermann, A. High quality sub-two cycle pulses from compression of supercontinuum generated in all-normal dispersion photonic crystal fiber. Opt. Express 2011, 19, 13873–13879. [Google Scholar] [CrossRef]
- Demmler, S.; Rothhardt, J.; Heidt, A.M.; Hartung, A.; Rohwer, E.G.; Bartelt, H.; Limpert, J.; Tünnermann, A. Generation of high quality, 1.3 cycle pulses by active phase control of an octave spanning supercontinuum. Opt. Express 2011, 19, 20151–20158. [Google Scholar] [CrossRef]
- Sukhoivanov, I.A.; Iakushev, S.O.; Shulika, O.V.; Andrade-Lucio, J.A.; Díez, A.; Andrés, M. Supercontinuum generation at 800 nm in all-normal dispersion photonic crystal fiber. Opt. Express 2014, 22, 30234–30250. [Google Scholar] [CrossRef]
- Xing, S.; Kharitonov, S.; Hu, J.; Brès, C.S. Linearly chirped mid-infrared supercontinuum in all-normal-dispersion chalcogenide photonic crystal fibers. Opt. Express 2018, 26, 19627–19636. [Google Scholar] [CrossRef] [PubMed]
- Malomed, B.A. Soliton Management in Periodic Systems; Springer: New York, NY, USA, 2006. [Google Scholar]
- Essiambre, R.J.; Raybon, G.; Mikkelsen, B. Optical Fiber Telecommunications IV B; Academic Press: New York, NY, USA, 2002; pp. 253–275. [Google Scholar]
- Zitelli, M.; Matera, F.; Settembre, M. 40-Gbit/s transmission in dispersion managed links with step-index fiber and linear compensation. Opt. Lett. 1999, 24, 1169–1171. [Google Scholar] [CrossRef] [PubMed]
- Hult, J. A fourth-order Runge–Kutta in the interaction picture method for simulating supercontinuum generation in optical fibers. J. Light. Technol. 2007, 25, 3770–3775. [Google Scholar] [CrossRef]
- Paschotta, R. Field Guide to Optical Fiber Technology; SPIE: Bellingham, WA, USA, 2010. [Google Scholar]
- Dong, X.; Yang, Q.; Spiess, C.; Bucklew, V.G.; Renninger, W.H. Stretched-pulse soliton Kerr resonators. Phys. Rev. Lett. 2020, 125, 033902. [Google Scholar] [CrossRef]
- Yang, Q.; Spiess, C.; Bucklew, V.G.; Renninger, W.H. Stretched-Pulse Solitons in Driven Fiber Resonators. In Proceedings of the CLEO: Science and Innovations, San Jose, CA, USA, 5–10 May 2019; Optical Society of America: Washington, DC, USA, 2019; p. SF1L-3. [Google Scholar]
- Lüpken, N.M.; Fallnich, C. Bandwidth-limited few-cycle pulses by nonlinear compression in a dispersion-alternating fiber. Appl. Phys. B 2020, 126, 1–7. [Google Scholar] [CrossRef]
- Travers, J.C.; Grigorova, T.F.; Brahms, C.; Belli, F. High-energy pulse self-compression and ultraviolet generation through soliton dynamics in hollow capillary fibres. Nat. Photonics 2019, 13, 547–554. [Google Scholar] [CrossRef] [Green Version]
- Zia, H. Enhanced Nonlinear Pulse Compression Sign-Alternating Dispersion Waveguides at Low Input Peak Powers. In Proceedings of the Mid-Infrared Coherent Sources, Washington, DC, USA, 16–20 November 2020; Optical Society of America: Washington, DC, USA, 2020; p. MM1C-4. [Google Scholar]








Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zia, H. Enhanced Pulse Compression within Sign-Alternating Dispersion Waveguides. Photonics 2021, 8, 50. https://doi.org/10.3390/photonics8020050
Zia H. Enhanced Pulse Compression within Sign-Alternating Dispersion Waveguides. Photonics. 2021; 8(2):50. https://doi.org/10.3390/photonics8020050
Chicago/Turabian StyleZia, Haider. 2021. "Enhanced Pulse Compression within Sign-Alternating Dispersion Waveguides" Photonics 8, no. 2: 50. https://doi.org/10.3390/photonics8020050