The Financial Stress Index: Identification of Systemic Risk Conditions
Abstract
:1. Introduction
2. Index Construction
2.1. Conceptual Definition of Stress
2.2. Indicators of Stress
| Market | Indicator Type | Variable | Indicator Data |
|---|---|---|---|
| Equity | Market Crashes—Equity Subsectors | SP5EENE D and SPLRCE G (S&P 500 energy); SP5EMAT D and SPLRCM G (S&P 500 materials); SP5EIND D and SPLRCI G (S&P 500 industrials); SP5ECOD D and SPLRCD G (S&P 500 cons. discretionary); SP5ECST D and SPLRCS G (S&P 500 consumer staples); SP5EHCR D and SPLRCA G (S&P 500 healthcare); SP5EFIN D and SPLRCF G (S&P 500 financials); SP5EINT D and SPLRCT G (S&P 500 information technology); SP5ETEL D and SPLRCL G (S&P 500 telecommunications); SP5EUTL D and SPLRCU G (S&P 500 utilities) | |
| Foreign Exchange | Crashes Market—Spot Currencies | UKDOLLRD and GBPUSDG (Pound sterling, UK); EUDOLLRD (Euro, Europe); CNUSDSCD and USDCADG (Dollar, Canada); MXUSDSP D and USDMXNG (Peso, Mexico); USDAUSPD and AUDUSDG (Dollar, Australia); JPYN1UDD and USDJPYG (Yen, Japan); BBZARSPD and USDZARG (Rand, South Africa) | |
| Covered Interest Spread | UKDOLLR D and GBPUSD G (Pound sterling, UK); EUDOLLR D (Euro, Europe); CNUSDSC D and USDCAD G (Dollar, Canada); MXUSDSP D and USDMXN G (Peso, Mexico); USDAUSP D and AUDUSD G (Dollar, Australia); JPYN1UD D and USDJPY G (Yen , Japan); BBZARSP D and USDZAR G (Rand, South Africa) | ||
| BBGBP3F D and GBPUSD3D G (Pound sterling, UK); TDEUR3M D (Euro, Europe); BBCAD3F D and USDCAD3D G (Dollar, Canada); USMXN3F D (Peso, Mexico); BBAUD3F D (Dollar, Australia); BBJPY3F D (Yen, Japan); BBZAR3F D (Rand, South Africa) | |||
| TRUK3MT D and ITGBR3D G (T-bill, UK); TREU3MT D (T-bill, Europe); TRCN3MT D and ITCAN3D G (T-bill, Canada); TRMX3MT D and ITMEX3D G (T-bill, Mexico); ADBR090 D (T-bill, Australia); TRJP3MT D and ITJPN3D G (T-bill, Japan); TRSA3MT D and ITZAF3D G (T-bill, South Africa) | |||
| FRTBS3M D (T-bill, USA) | |||
| Credit | Financing Spread | FRMCAAA D (Corporate bond yield); FRCPF3M D, FRFP3MT D, and IPUSAC3D G (Financial commercial paper yield) | |
| TRUS10C D (10 year government bond); FRTBS3M D (T-bill, USA) | |||
| Liquidity Spread—US$ Deposit Spread | ECUSD3M(IO) D (3 month dollar deposits, offered yield) | ||
| ECUSD3M(IB) D (3 month dollar deposits, bid yield) | |||
| Yield Curve Spread—Treasuries | TRUS10C D (10 year government bond) | ||
| FRTBS3M D (T-bill, USA) | |||
| Funding | Financing Spread—Interbank Liquidity | B5USD3M D and IBUSA3D G (US Interbank rate—interbank liquidity spread and interbank cost of borrowing spread); LHFINAN D and FRMCAAA D (financial bond yield—bank bond spread) | |
| FRTBS3M D (US T-bill - interbank liquidity spread); USFDTRG D (fed. funds target rate - interbank cost of borrowing spread); TRUS10C D (10 year government bond - bank bond spread) | |||
| Market Beta—Financial Subsector | SP5EFIN D (S&P 500 financials); SPLRCBK G (banking S&P 500 index) | ||
| S.PCOMP D and SPXD G (S&P 500 index) | |||
| Securitization | Financing Spread—Sec. Submarkets | LHGNM30 D and WIMRT30Y G (residential MBS); LHCRING D and LHIGCMB D (commercial MBS); MLABSMF D (asset backed securities) | |
| FRTCM7Y D (7 year constant maturity treasury yield—RMBS); FRTCM10 D (10 year constant maturity treasury yield—CMBS); FRTCM5Y D (5 year constant maturity treasury yield—ABS) | |||
| Real Estate | Return Spread | WIREI G (residential real estate); USNPIRN D and SPREITW G (commercial real estate) | |
| FRTCM3Y D (3 year gov. bond yield) |
2.2.1. Financing Spread
2.2.2. Market Beta
2.2.3. Market Crashes
2.2.4. Covered Interest Spread
2.2.5. Liquidity Spread
2.2.6. Yield Curve Spread
2.2.7. Return Spread
2.3. Indicator Transformation
| Name | N | Minimum | Maximum | Mean | Std. Deviation | Skewness | Kurtosis | Kolmogorov−Smirnov A |
|---|---|---|---|---|---|---|---|---|
| EQ_SP5EENE_DD | 7690 | 0.46 | 1.00 | 0.92 | 0.09 | −2.15 (0.03) | 5.72 (0.06) | 0.18 *** |
| EQ_SP5EMAT_DD | 6732 | 0.38 | 1.00 | 0.91 | 0.10 | −2.18 (0.03) | 5.79 (0.06) | 0.19 *** |
| EQ_SP5EIND_DD | 11857 | 0.38 | 1.00 | 0.92 | 0.10 | −1.9 (0.02) | 3.96 (0.04) | 0.2 *** |
| EQ_SP5ECOD_DD | 11857 | 0.47 | 1.00 | 0.92 | 0.09 | −1.64 (0.02) | 2.74 (0.04) | 0.19* ** |
| EQ_SP5ECST_DD | 11857 | 0.54 | 1.00 | 0.93 | 0.07 | −1.66 (0.02) | 2.96 (0.04) | 0.19 *** |
| EQ_SP5EHCR_DD | 7425 | 0.62 | 1.00 | 0.93 | 0.08 | −1.14 (0.03) | 0.38 (0.06) | 0.17 *** |
| EQ_SP5EFIN_DD | 11857 | 0.22 | 1.00 | 0.90 | 0.12 | −2.17 (0.02) | 6.05 (0.04) | 0.19 *** |
| EQ_SP5EINT_DD | 7690 | 0.33 | 1.00 | 0.89 | 0.14 | −1.81 (0.03) | 2.86 (0.06) | 0.2 *** |
| EQ_SP5ETEL_DD | 6732 | 0.41 | 1.00 | 0.89 | 0.12 | −1.52 (0.03) | 1.75 (0.06) | 0.17 *** |
| EQ_SP5EUTL_DD | 11857 | 0.47 | 1.00 | 0.92 | 0.09 | −1.94 (0.02) | 3.56 (0.04) | 0.19 *** |
| FX_GBP_DD | 11857 | 0.67 | 1.00 | 0.93 | 0.07 | −1.28 (0.02) | 1.14 (0.04) | 0.14 *** |
| FX_EUR_DD | 11857 | 0.68 | 1.00 | 0.92 | 0.06 | −0.79 (0.02) | −0.11 (0.04) | 0.12 *** |
| FX_ZAR_DD | 11857 | 0.51 | 1.00 | 0.89 | 0.09 | −0.86 (0.02) | 0.44 (0.04) | 0.12 *** |
| FX_CAD_DD | 11857 | 0.71 | 1.00 | 0.96 | 0.04 | −1.84 (0.02) | 5.79 (0.04) | 0.13 *** |
| FX_AUD_DD | 11857 | 0.63 | 1.00 | 0.93 | 0.06 | −1.27 (0.02) | 1.87 (0.04) | 0.15 *** |
| FX_MXN_DD | 11857 | 0.15 | 1.00 | 0.86 | 0.18 | −1.68 (0.02) | 1.98 (0.04) | 0.23 *** |
| FX_JPY_DD | 11857 | 0.75 | 1.00 | 0.93 | 0.06 | −0.91 (0.02) | 0.04 (0.04) | 0.13 *** |
| FX_GBP_CIS | 11857 | −0.04 | 0.08 | 0.02 | 0.02 | 0.66 (0.02) | 0.15 (0.04) | 0.1 *** |
| FX_CAD_CIS | 11857 | −0.02 | 0.06 | 0.01 | 0.01 | 0.4 (0.02) | −0.08 (0.04) | 0.07 *** |
| FX_EUR_CIS | 4302 | −0.02 | 0.05 | 0.00 | 0.01 | 0.3 (0.04) | 0.4 (0.07) | 0.04 *** |
| FX_MXN_CIS | 4826 | −0.02 | 0.30 | 0.05 | 0.04 | 2.21 (0.04) | 5.83 (0.07) | 0.23 *** |
| FX_ZAR_CIS | 8276 | −0.02 | 0.14 | 0.05 | 0.02 | −0.2 (0.03) | 0.63 (0.05) | 0.04 *** |
| FX_JPY_CIS | 8276 | −0.07 | 0.04 | −0.01 | 0.02 | −0.07 (0.03) | −1.01 (0.05) | 0.07 *** |
| FX_AUD_CIS | 7968 | −0.03 | 0.11 | 0.03 | 0.02 | 0.96 (0.03) | 0.5 (0.05) | 0.11 *** |
| CR_CBS | 11857 | −0.01 | 0.03 | 0.01 | 0.01 | 0.20 (0.02) | -0.06 (0.04) | 0.06 *** |
| CR_CPS | 11857 | 0.00 | 0.05 | 0.01 | 0.01 | 2.6 (0.02) | 9.87 (0.04) | 0.18 *** |
| CR_LIQS_MA | 10535 | 0.00 | 0.00 | 0.00 | 0.00 | 1.78 (0.02) | 3.76 (0.05) | 0.24 *** |
| CR_TYC_MA | 11857 | −0.03 | 0.05 | 0.02 | 0.01 | −0.61 (0.02) | −0.1 (0.04) | 0.07 *** |
| IB_LS | 11857 | 0.00 | 0.07 | 0.01 | 0.01 | 1.89 (0.02) | 4.46 (0.04) | 0.16 *** |
| IB_CS | 11603 | −0.05 | 0.07 | 0.01 | 0.01 | 1.61 (0.02) | 9.17 (0.05) | 0.2 *** |
| IB_BBS | 11857 | −0.01 | 0.07 | 0.01 | 0.01 | 2.95 (0.02) | 14.06 (0.04) | 0.14 *** |
| IB_FB | 11857 | −0.16 | 0.69 | 0.29 | 0.13 | 0.15 (0.02) | 0.21 (0.04) | 0.02 *** |
| RE_RRE | 11857 | −0.13 | 0.12 | −0.01 | 0.05 | 0.06 (0.02) | −0.92 (0.04) | 0.04 *** |
| RE_CRE | 11357 | −0.58 | 0.15 | −0.02 | 0.14 | −2.15 (0.02) | 4.81 (0.05) | 0.17 *** |
| SEC_CMBS | 5848 | −0.01 | 0.15 | 0.01 | 0.02 | 3.66 (0.03) | 15.89 (0.06) | 0.23 *** |
| SEC_RMBS | 11857 | −0.01 | 0.04 | 0.01 | 0.00 | 0.38 (0.02) | 2.19 (0.05) | 0.05 *** |
| SEC_ABS | 6392 | −0.01 | 0.09 | 0.01 | 0.01 | 3.78 (0.03) | 17.19 (0.06) | 0.24 *** |
2.4. Aggregating Financial System Stress
3. CFSI Calibration


| Name | TP | FP | TN | FN | T1 | T2 | IV | NTSR | µ | ||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Panel 1: Quarterly ( and 3 bins were used for IV) | |||||||||||||
| 1 | Credit Weights | 1.01 | 12 | 2 | 72 | 6 | 0.33 | 0.03 | 0.33 | 0.04 | 0.8 | 0.1 | 0.64 |
| 2 | Principal Component Weights | 1.04 | 12 | 3 | 71 | 6 | 0.33 | 0.04 | 0.18 | 0.06 | 0.8 | 0.1 | 0.63 |
| 3 | Equal Market Weights | 0.56 | 13 | 11 | 63 | 5 | 0.28 | 0.15 | 1.08 | 0.21 | 0.8 | 0.09 | 0.57 |
| 4 | Portfolio Theoretic Weights | 0.59 | 9 | 6 | 68 | 9 | 0.5 | 0.08 | 0.49 | 0.16 | 0.8 | 0.07 | 0.42 |
| Panel 2: Monthly ( and 3 bins were used for IV) | |||||||||||||
| 1 | Equal Market Weights | 0.68 | 36 | 23 | 202 | 17 | 0.32 | 0.1 | 0.62 | 0.15 | 0.8 | 0.09 | 0.57 |
| 2 | Principal Component Weights | 0.98 | 33 | 14 | 211 | 20 | 0.38 | 0.06 | 0.27 | 0.1 | 0.8 | 0.08 | 0.56 |
| 3 | Credit Weights | 0.78 | 33 | 22 | 203 | 20 | 0.38 | 0.1 | 0.71 | 0.16 | 0.8 | 0.08 | 0.52 |
| 4 | Portfolio Theoretic Weights | 1.03 | 20 | 7 | 218 | 33 | 0.62 | 0.03 | 0.16 | 0.08 | 0.8 | 0.05 | 0.34 |
| Panel 3: Weekly ( and 4 bins were used for IV) | |||||||||||||
| 1 | Principal Component Weights | 0.88 | 163 | 95 | 854 | 96 | 0.37 | 0.1 | 0.52 | 0.16 | 0.8 | 0.08 | 0.5 |
| 2 | Credit Weights | 0.77 | 154 | 93 | 856 | 105 | 0.41 | 0.1 | 0.66 | 0.16 | 0.8 | 0.07 | 0.46 |
| 3 | Equal Market Weights | 0.65 | 153 | 113 | 836 | 106 | 0.41 | 0.12 | 0.75 | 0.2 | 0.8 | 0.07 | 0.43 |
| 4 | Portfolio Theoretic Weights | 0.62 | 105 | 66 | 883 | 154 | 0.59 | 0.07 | 0.22 | 0.17 | 0.7 | 0.04 | 0.3 |
| Panel 4: Daily ( and 4 bins were used for IV) | |||||||||||||
| 1 | Principal Component Weights | 0.86 | 1207 | 601 | 5872 | 781 | 0.39 | 0.09 | 0.38 | 0.15 | 0.7 | 0.08 | 0.48 |
| 2 | Credit Weights | 0.73 | 1174 | 661 | 5812 | 814 | 0.41 | 0.1 | 0.62 | 0.17 | 0.7 | 0.07 | 0.45 |
| 3 | Equal Market Weights | 0.64 | 1132 | 761 | 5712 | 856 | 0.43 | 0.12 | 0.6 | 0.21 | 0.7 | 0.07 | 0.41 |
| 4 | Portfolio Theoretic Weights | 0.65 | 744 | 401 | 6072 | 1244 | 0.63 | 0.06 | 0.15 | 0.17 | 0.7 | 0.05 | 0.29 |
4. CFSI Interpretation
4.1. Decomposition of Stress
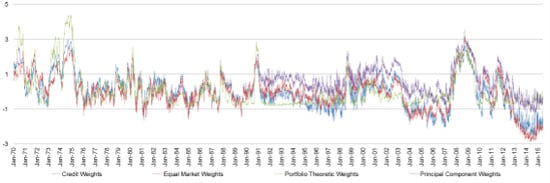
4.1.1. Credit Weights


4.1.2. Market Components


4.2. Historical Relevance of Stress
4.2.1. Stress Regimes
| Break Test | Scaled F-Statistic | Critical Value ***A | Break Date |
|---|---|---|---|
| 0 vs. 1 *** | 2773.19 | 13.00 | 06/24/1980 |
| 1 vs. 2 *** | 1368.53 | 14.51 | 12/07/2010 |
| 2 vs. 3 *** | 669.86 | 15.44 | 05/09/1975 |
| 3 vs. 4 *** | 166.92 | 15.73 | 05/23/2006 |
| 4 vs. 5 *** | 736.42 | 16.39 | 04/11/1991 |
| 5 vs. 6 *** | 184.09 | 16.60 | 07/23/1998 |
| 6 vs. 7 *** | 47.12 | 16.78 | 03/19/1986 |
| 7 vs. 8 | 0.00 | 16.90 | not found |

4.2.2. Links to Regulation

5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- G. Caprio, and D. Klingebiel. Bank Insolvencies: Cross Country Experiences. World Bank Policy Research Working Paper No. 1620; Washington, DC, USA: The Work Bank, 1996. [Google Scholar]
- A. Demirgüç-Kunt, and E. Detragiache. “The determinants of banking crises in developing and developed countries.” IMF Staff Pap. 45 (1998): 81–109. [Google Scholar] [CrossRef]
- O. De Bandt, and P. Hartmann. Systemic risk: A Survey. European Central Bank Working Paper No. 35; Frankfurt, Germany: European Central Bank, 2000. [Google Scholar]
- Y. Ishihara. Quantitative Analysis of Crisis: Crisis Identification and Causality. World Bank Policy Research Working Paper No. 3598; Washington, DC, USA: The Work Bank, 2005. [Google Scholar]
- E.P. Davis, and D. Karim. “Comparing early warning systems for banking crises.” J. Financ. Stab. 4 (2008): 89–120. [Google Scholar] [CrossRef]
- M.D. Bordo, M. Dueker, and D. Wheelock. Aggregate Price Shocks and Financial Instability: An Historical Analysis. Federal Reserve Bank of St. Louis Working Paper No. 005B; St. Louis, MO, USA: Federal Reserve Bank of St. Louis, 2000. [Google Scholar]
- M. Rosenberg. “Financial Conditions Watch, Global Financial Market Trends and Policy. Bloomberg LLP.” Available online: http://www.ssc.wisc.edu/~mchinn/fcw_sep112009.pdf (accessed on 1 July 2015).
- W. English, K. Tsatsaronis, and E. Zoli. “Assessing the predictive power of measures of financial conditions for macroeconomic variables.” In Investigating the Relationship between the Financial and Real Economy. BIS Paper No. 22; Basel, Switzerland: Bank for International Settlements (BIS), 2005, pp. 228–252. [Google Scholar]
- A. Swiston. A U.S. Financial Conditions Index. International Monetary Fund Working Paper No. 16; Washington, DC, USA: International Monetary Fund, 2008. [Google Scholar]
- J.B. Thomson. On Systemically Important Financial Institutions and Progressive Systemic Mitigation. FRB of Cleveland Policy Discussion Paper No. 7; Cleveland, OH, USA: FRB of Cleveland, 2007. [Google Scholar]
- N. Liang. “Systemic risk monitoring and financial stability.” J. Money Credit Bank. 45 (2013): 129–135. [Google Scholar] [CrossRef]
- E.S. Rosengren. “Defining financial stability, and some policy implications of applying the definition.” In Keynote Remarks. Stanford, CA, USA: Stanford Finance Forum Graduate School of Business, 2011. [Google Scholar]
- G. Schinasi. “Understanding Financial Stability: Towards a Practical Framework.” In Proceedings of the Seminar on Current Developments in Monetary and Financial Law, Washington, DC, USA, 23–27 October 2006.
- J. Laker. “Monitoring financial system stability.” Reserv. Bank Aust. Bull. 10 (1999): 40–46. [Google Scholar]
- R.W. Ferguson. “Should financial stability be an explicit central bank objective.” In Proceedings of the International Monetary Fund Conference: Monetary Stability, Financial Stability and the Business Cycle, Washington, DC, USA, 27–28 October 2003; pp. 208–223.
- A. Crockett. “Why is financial stability a goal of public policy? ” Fed. Reserv. Bank Kansas City Econ. Rev. 82 (1997): 5–22. [Google Scholar]
- F.S. Mishkin. “The causes and propagation of financial instability: Lessons for policymakers.” In Maintaining Financial Stability in a Global Economy. Kansas City, MO, USA: Federal Reserve Bank of Kansas City, 1997, pp. 55–96. [Google Scholar]
- J. Simmie, and R. Martin. “The economic resilience of regions: Towards an evolutionary approach.” Camb. J. Regions Econ. Soc. 3 (2010): 27–43. [Google Scholar] [CrossRef]
- G.L. Kaminsky, and C.M. Reinhart. “The twin crises: The causes of banking and balance-of-payments problems.” Am. Econ. Rev. 89 (1999): 473–500. [Google Scholar] [CrossRef] [Green Version]
- A. Demirgüç-Kunt, and E. Detragiache. Cross-Country Empirical Studies of Systemic Bank Distress: A Survey. IMF Working Paper No. 96; Washington, DC, USA: International Monetary Fund (IMF), 2005. [Google Scholar]
- L. Laeven, and F. Valencia. Systemic Banking Crises: A New Database. IMF Working Paper No. 224; Washington, DC, USA: International Monetary Fund (IMF), 2008. [Google Scholar]
- C. Reinhart, and K. Rogoff. This Time Is Different: A Panoramic View of Eight Centuries of Financial Crises. NBER Working Paper No. 13882; Cambridge, MA, USA: National Bureau of Economic Research (NBER), 2008. [Google Scholar]
- W.A. Brock, and C.H. Hommes. “A rational route to randomness.” Econometrica 65 (1997): 1059–1095. [Google Scholar] [CrossRef]
- W.A. Brock, and C.H. Hommes. “Heterogeneous beliefs and routes to chaos in a simple asset pricing model.” J. Econ. Dyn. Control 22 (1998): 1235–1274. [Google Scholar] [CrossRef]
- C.H. Hommes. “Financial markets as nonlinear adaptive evolutionary systems.” Quant. Financ. 1 (2001): 149–167. [Google Scholar] [CrossRef]
- P. Aghion, and P. Howitt. “A model of growth through creative destruction.” Econometrica 60 (1992): 323–351. [Google Scholar] [CrossRef]
- P. Howitt, A. Kirman, A. Leijonhufvud, P. Mehrling, and D. Colander. “Beyond DSGE models: Toward an empirically based macroeconomics.” Am. Econ. Rev. 98 (2008): 236–240. [Google Scholar]
- J.D. Farmer. “Market force, ecology and evolution.” Ind. Corp. Chang. 11 (2002): 895–953. [Google Scholar] [CrossRef]
- J.D. Farmer, P. Patelli, and I.I. Zovko. “The predictive power of zero intelligence in financial markets.” Proc. Natl. Acad. Sci. USA 102 (2005): 2254–2259. [Google Scholar] [CrossRef] [PubMed]
- D. Hendricks, J. Kambhu, and P. Mosser. “Systemic Risk and the Financial System.” Fed. Reserv. Bank N. Y. Econ. Policy Rev. 13 (2007): 65–80. [Google Scholar]
- J. Kambhu, S. Weidman, and N. Krishnan. “Introduction: New directions for understanding systemic risk.” Fed. Reserv. Bank N. Y. Econ. Policy Rev. 13 (2007): 3–14. [Google Scholar]
- M. Illing, and Y. Liu. “Measuring financial stress in a developed country: An application to Canada.” J. Financ. Stab. 2 (2006): 243–265. [Google Scholar] [CrossRef]
- D. Gramlich, G. Miller, M. Oet, and S. Ong. “Early Warning Systems for Systemic Banking Risk: Critical Review and Modeling Implications.” Bank. Bank Syst. 5 (2010): 199–211. [Google Scholar]
- X. Freixas, and J.-C. Rochet. Microeconomics of Banking, 2nd ed. Cambridge, MA, USA: The MIT Press, 2008. [Google Scholar]
- B. Bernanke, and M. Gertler. “Inside the black box: The credit channel of monetary policy transmission.” J. Econ. Perspect. 9 (1995): 27–48. [Google Scholar] [CrossRef]
- B.S. Bernanke, and M. Gertler. “Financial fragility and economic performance.” Q. J. Econ. 105 (1990): 97–114. [Google Scholar] [CrossRef]
- B. Holmström, and J. Tirole. “Financial intermediation, loanable funds, and the real sector.” Q. J. Econ. 112 (1997): 663–691. [Google Scholar] [CrossRef]
- P. Bolton, and X. Freixas. “Equity, bonds, and bank debt: Capital structure and financial market equilibrium under asymmetric information.” J. Political Econ. 108 (2000): 324–351. [Google Scholar] [CrossRef]
- S.A. Patel, and A. Sarkar. “Crises in developed and emerging stock markets.” Financ. Anal. J. 54 (1998): 50–61. [Google Scholar] [CrossRef]
- M.P. Taylor. “Covered interest arbitrage and market turbulence.” Econ. J. 99 (1989): 376–391. [Google Scholar] [CrossRef]
- T. Mancini-Griffoli, and A. Ranaldo. “Limits to arbitrage during the crisis: Funding liquidity constraints and covered interest parity.” Available online: http://papers.ssrn.com/sol3/papers.cfm?abstract_id=1569504. (accessed on 5 August 2015).
- N. Baba, and F. Packer. “From turmoil to crisis: Dislocations in the FX swap market before and after the failure of Lehman Brothers.” J. Int. Money Financ. 28 (2009): 1350–1374. [Google Scholar] [CrossRef]
- A. Crockett. “Market liquidity and financial stability.” Banq. Fr. Financ. Stab. Rev. 11 (2008): 13–17. [Google Scholar]
- J. Caruana, and L. Kodres. “Liquidity in global markets.” Banq. Fr. Financ. Stab. Rev. 11 (2008): 65–74. [Google Scholar]
- A. Bervas. “Market liquidity and its incorporation into risk management.” Banq. Fr. Financ. Stab. Rev. 8 (2006): 63–79. [Google Scholar]
- L. Chen, D.A. Lesmond, and J. Wei. “Corporate yield spreads and bond liquidity.” J. Financ. 62 (2007): 119–149. [Google Scholar] [CrossRef]
- D. Hou, and D.R. Skeie. LIBOR: Origins, Economics, Crisis, Scandal, and Reform. FRB of New York Staff Report No. 667; New York, NY, USA: FRB of New York, 2014. [Google Scholar]
- A. Estrella, and G. Hardouvelis. “The term structure as a predictor of real economic activity.” J. Financ. 46 (1991): 555–576. [Google Scholar] [CrossRef]
- A. Estrella, and F. Mishkin. “The yield curve as a predictor of U.S. recessions.” Fed. Reserv. Bank N. Y. Curr. Issues Econ. Financ. 2 (1996): 1–6. [Google Scholar] [CrossRef]
- J. Haubrich, and T. Bianco. The Yield Curve as a Predictor of Economic Growth. Cleveland, OH, USA: Federal Reserve Bank of Cleveland, 2011. [Google Scholar]
- S. Gilchrist, and E. Zakrajšek. Credit Spreads and Business Cycle Fluctuations. NBER Working Paper No. w17021; Cambridge, MA, USA: National Bureau of Economic Research (NBER), 2011. [Google Scholar]
- M. Goodfriend. “Financial Stability, Deflation, and Monetary Policy.” Monet. Econ. Stud. 19 (2001): 143–176. [Google Scholar] [CrossRef]
- A. Spanos. Probability Theory and Statistical Inference: Econometric Modeling with Observational Data. Cambridge, UK: Cambridge University Press, 1999. [Google Scholar]
- R. Koenker, and G. Bassett Jr. “Regression quantiles.” Econometrica 46 (1978): 33–50. [Google Scholar] [CrossRef]
- R. Koenker. Quantile Regression. Cambridge, UK: Cambridge University Press, 2005. [Google Scholar]
- D. Hollo, M. Kremer, and M. Lo Duca. CISS-A Composite Indicator of Systemic Stress in the Financial System. ECB Working Paper Series No. 1426; Frankfurt, Germany: European Central Bank (ECB), 2012. [Google Scholar]
- M. Illing, and Y. Liu. An Index of Financial Stress for Canada. Bank of Canada Working Paper No. 14; Ottawa, ON, Canada: Bank of Canada, 2003. [Google Scholar]
- J.F. Hair, W.C. Black, B.J. Babin, R.E. Anderson, and R.L. Tatham. Multivariate Data Analysis, 7th ed. Upper Saddle River, NJ, USA: Pearson Prentice Hall, 2009. [Google Scholar]
- S.A. Brave, and R.A. Butters. “Monitoring financial stability: A financial conditions index approach.” Econ. Perspect. 35 (2011): 22–43. [Google Scholar]
- M.V. Oet, J. Dooley, D. Gramlich, P. Sarlin, and S. Ong. Evaluating the Information Value for Measures of Systemic Conditions. Federal Reserve Bank of Cleveland Working Paper No. 15/13; Cleveland, OH, USA: Federal Reserve Bank of Cleveland, 2015. [Google Scholar]
- G. Kaminsky, S. Lizondo, and C.M. Reinhart. “Leading indicators of currency crises.” IMF Staff Pap. 45 (1998): 1–48. [Google Scholar] [CrossRef] [Green Version]
- N. Siddiqi. Credit Risk Scorecards: Developing and Implementing Intelligent Credit Scoring. Cary, NC, USA: SAS Institute, 2006, pp. 79–83. [Google Scholar]
- L. Laeven, and F. Valencia. “Systemic banking crises database.” IMF Econ. Rev. 61 (2012): 225–270. [Google Scholar] [CrossRef]
- H.A. Simon. “The Architecture of Complexity.” Proc. Am. Philos. Soc. 106 (1962): 467–482. [Google Scholar]
- J. Bai, and P. Perron. “Estimating and testing linear models with multiple structural changes.” Econometrica 66 (1998): 47–78. [Google Scholar] [CrossRef]
- J. Bai, and P. Perron. “Critical values for multiple structural change tests.” Econom. J. 6 (2003): 72–78. [Google Scholar] [CrossRef]
- “FDIC website. ” Available online: https://www.fdic.gov/bank/historical/sandl/ (accessed on 5 July 2015).
- J.A. Miron. “Financial panics, the seasonality of the nominal interest rate, and the founding of the Fed.” Am. Econ. Rev. 76 (1986): 125–140. [Google Scholar]
- E.W. Kemmerer. Seasonal Variations in the Relative Demand for Money and Capital in the United States; Washington, DC, USA: Government Printing Office, 1910.
- C.W. Calomiris. U.S. Bank Deregulation in Historical Perspective. Cambridge, UK: Cambridge University Press, 2000. [Google Scholar]
- 2Brock and Hommes [23,24] study financial markets as adaptive belief systems. Hommes [25] extends this approach to markets as nonlinear adaptive evolutionary systems. See Aghion and Howitt [26] and Howitt et al. [27] for complexity-based macroeconomic models in addition to Farmer [28] and Farmer et al. [29] for complexity-based modeling of financial markets.
- 3Despite similarities between the financing spread and the return spread a key difference is that the former measures the expected rate of return associated with purchasing an asset whereas the latter calculates the realized spread.
- 4Note that market crash indicators for the equity market and return spread indicators attempt to capture the realized downside exposure of designated markets. As a result, we invert the CDF transformation for these series, i.e., we use . For a price series, the observation with the worst realized return under the original CDF would yield a value close to zero instead of the desired value . Similarly, Yield Curve Spread indicators are also inverted based upon literature which finds that flat and inverted yield curves correspond to slow growth prospects.
- 5Specifically, note that since the CDF transformation depends only upon the rank ordering of observations, while .
- 6Namely, we consider the Chicago Board Options Exchange’s VIX, Merrill Lynch’s MOVE, and JP Morgan’s global FX volatility (JPMVXYGL), alongside three calculated volatility measures for corporate bonds, real estate, and securitization from 1 May 1992 to 30 June 2015.
- 7We select such that approximately 20% of observations will indicate a crisis and fix K = 2, and L = 2.
- 8The IV metric calculation divides the sample into n bins and becomes unstable if there are not good and bad classifications in each bin.
- 9Oet et al. [60] recommend selecting τ and μ for each stress measure in order to maximize the relative usefulness of the series.
- 10The stress period marks the 1973–1975 US crisis that included such momentous events as the fall of the Bretton Woods system, the 1973 oil crisis, the 1973–1975 recession, and the 1973–1974 stock market crash.
- 11For the equity market several sub-market indicators are not available 1970, and market capitalization data was not found before 1995. Before 1995 we use the earliest available information to infer the size of each sector relative to the set of sectors for which indicator data is available.
- 12Similarly data is not available to parse out the foreign exchange weight to each country prior to 1977. To enable some historical estimate of stress, the weights for each country from 1977 are applied backwards through 1970.
- 13Note that the aggregate size of the equity and foreign exchange markets relative to the financial system is available through the Financial Accounts of the US Z.1 Report. However, historical estimates of stress within the equity and foreign exchange markets are naturally limited by the opacity of relative weight within these markets.
- 14The Bank Holding Company Act of 1956 and Glass–Steagall Act of 1993 prevented US financial intermediaries from expanding their activities to become universal banks.
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Oet, M.V.; Dooley, J.M.; Ong, S.J. The Financial Stress Index: Identification of Systemic Risk Conditions. Risks 2015, 3, 420-444. https://doi.org/10.3390/risks3030420
Oet MV, Dooley JM, Ong SJ. The Financial Stress Index: Identification of Systemic Risk Conditions. Risks. 2015; 3(3):420-444. https://doi.org/10.3390/risks3030420
Chicago/Turabian StyleOet, Mikhail V., John M. Dooley, and Stephen J. Ong. 2015. "The Financial Stress Index: Identification of Systemic Risk Conditions" Risks 3, no. 3: 420-444. https://doi.org/10.3390/risks3030420