Delivering Left-Skewed Portfolio Payoff Distributions in the Presence of Transaction Costs †
Abstract
:1. Introduction
2. Wealth dynamics
3. Performance Measures
3.1. Aggregate Reward
3.2. Discussion

4. Investment Strategies and Pension Distributions without Transaction Costs
4.1. Optimal strategies


4.2. Pension distributions

| Statitic | Caut.-Relax. | Merton |
|---|---|---|
| Mode of | $93,790 | $55,300 |
| Mean of | $74,922 | $86,596 |
| Median of | $83,373 | $73,082 |
| Std. dev. of | $21,723 | $55,042 |
| Coeff. of skew. | –1.017 | 2.164 |
| P | 0 | 0.273 |
| P | 0.562 | 0.438 |
| P | 0.1077 | 0.15 |
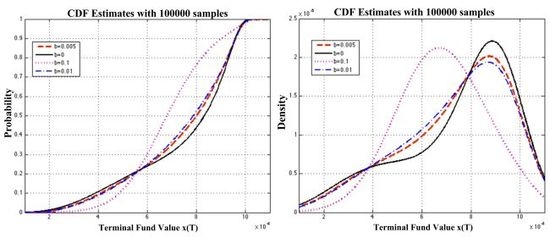
5. Cautious-relaxed strategies and pension distributions with transaction costs
5.1. Optimal strategies



5.2. Pension Distributions

| Statistic | Merton | |||||
|---|---|---|---|---|---|---|
| Mean of | $74,922 | $74,000 | $73,657 | $70,651 | $68,493 | $86,596 |
| Median of | $83,373 | $80,133 | $78,815 | $71,297 | $67,966 | $73,082 |
| Std. dev. of | $21,723 | $20,741 | $20,464 | $18,108 | $15,640 | $55,042 |
| Coeff. of skew. of | –1.017 | –0.8499 | –0.78 | –0.331 | 0.0158 | 2.164 |
| P | 0.562 | 0.503 | 0.475 | 0.333 | 0.233 | 0.438 |
| P | 0.1077 | 0.0938 | 0.0875 | 0.0561 | 0.0317 | 0.15 |
5.3. Advice
6. Conclusion
Acknowledgments
Conflicts of Interest
A. Parameters
| r | α | σ | c |
|---|---|---|---|
| 0.05 | 0.085 | 0.2 | .005 |
B. SOCSol and Yield Distributions
C. The Merton Investor
C.1. The Classic Utility Measure
C.2. The Distribution
D. Why Zero-Investment Can Be Profitable in This Model
References
- T. Bali, N. Cakici, and R. Whitelaw. “Maxing out: Stocks as lotteries and the cross-section of expected returns.” J. Financ. Econ. 99 (2011): 427–446. [Google Scholar] [CrossRef]
- N. Barberis, and M. Huang. “Stocks as Lotteries: The Implications of Probability Weighting for Security Prices.” Am. Econ. Rev. 98 (2008): 2066–2100. [Google Scholar] [CrossRef]
- P. Brockett, and Y. Kahane. “Risk, Return, Skewness and Preference.” Manag. Sci. 38 (1992): 851–866. [Google Scholar] [CrossRef]
- R.C. Merton. “Optimum consumption and portfolio rules in a continuous-time model.” J. Econ. Theory 3 (1971): 373–413. [Google Scholar] [CrossRef]
- M. Annunziato, and A. Borzì. “Optimal control of probability density functions of stochastic processes.” Math. Model. Anal. 15 (2010): 393–407. [Google Scholar] [CrossRef]
- C. Bernard, J.S. Chen, and S. Vanduffel. “Rationalizing investors’ choices.” J. Math. Econ. 59 (2015): 10–23. [Google Scholar] [CrossRef]
- J. Outreville. “Meaning of Risk.” Geneva Pap. Risk Insur. Issues Pract. 39 (2014): 768–781. [Google Scholar] [CrossRef]
- B. Jacobs, and K. Levy. “Traditional Optimization Is Not Optimal for Leverage-Averse Investors.” J. Portf. Manag. 40 (2014): 30–40. [Google Scholar] [CrossRef]
- D. Goldstein, E. Johnson, and W. Sharpe. “Choosing Outcomes versus Choosing Products: Consumer-Focused Retirement Investment Advice.” J. Consum. Res. 35 (2008): 440–456. [Google Scholar] [CrossRef]
- X. He, and X. Zhou. “Portfolio choice via quantiles.” Math. Finance 21 (2011): 203–231. [Google Scholar] [CrossRef]
- J.B. Krawczyk. “On loss-avoiding payoff distributions in a dynamic portfolio management problem.” J. Risk Finance 9 (2008): 151–172. [Google Scholar] [CrossRef]
- J.D. Azzato, and J.B. Krawczyk. “Parallel SOCSol: A Parallel MATLAB (R) package for approximating the solution to a continuous-time stochastic optimal control problem.” Technical report, Victoria University of Wellington. 2008. Available online: http://researcharchive.vuw.ac.nz/handle/10063/387 (accessed on 18 August 2015).
- J.B. Krawczyk. “Numerical Solutions to Lump-Sum Pension Fund Problems That Can Yield Left-Skewed Fund Return Distributions.” In Optimal Control and Dynamic Games. Edited by C. Deissenberg and R.F. Hartl. Dordrecht, The Netherlands: Springer, 2005, Chapter 11; pp. 155–176. [Google Scholar]
- J. Foster. “Target Variation in a Loss Avoiding Pension Fund Problem Problem.” Technical report, Victoria University of Wellington. 2011. Available online: http://mpra.ub.uni-muenchen.de/36177/1/writeup.pdf (accessed on 18 August 2015).
- J. Azzato, J. Krawczyk, and C. Sissons. “On loss-avoiding lump-sum pension optimization with contingent targets.” Working Paper Series 1532, Victoria University of Wellington, School of Economics and Finance. 2011. Available online: http://EconPapers.repec.org/RePEc:vuw:vuwecf:1532 (accessed on 18 August 2015).
- J.B. Krawczyk. “A Markovian approximated solution to a portfolio management problem.” Inf. Technol. Econ. Manag. 2001. Available online: http://personal.victoria.ac.nz/jacek_krawczyk/somepapers/portfitem.pdf (accessed on 20 August 2015).
- J. Foster, and J.B. Krawczyk. “Sensitivity of Cautious-Relaxed Investment Policies to Target Variation.” Working Paper Series 1532, Victoria University of Wellington, School of Economics and Finance. 2013. Available online: http://EconPapers.repec.org/RePEc:vuw:vuwecf:1532 (accessed on 18 August 2015).
- W.H. Fleming, and R.W. Rishel. Deterministic and Stochastic Optimal Control. New York, NY, USA: Springer, 1975. [Google Scholar]
- V. Gaitsgory. “Suboptimization of singularly perturbed control systems.” SIAM J. Control Optim. 30 (1992): 1228–1249. [Google Scholar] [CrossRef]
- D. Blake. “Portfolio choice models of pension funds and life assurance companies: Similarities and differences.” Geneva Pap. Risk Insur. Issues Pract. 24 (1999): 327–357. [Google Scholar] [CrossRef]
- V. Gaitsgory. “Averaging and near viability of singularly perturbed control systems.” J. Convex Anal. 13 (2006): 329–352. [Google Scholar]
- A.B. Berkelaar, R. Kouwenberg, and T. Post. “Optimal Portfolio Choice Under Loss Aversion.” Rev. Econ. Stat. 86 (2004): 973–987. [Google Scholar] [CrossRef]
- K.F.C. Yiu. “Optimal portfolios under a value-at-risk constraint.” J. Econ. Dyn. Control 28 (2004): 1317–1334. [Google Scholar] [CrossRef]
- E. Bogentoft, H.E. Romeijn, and S. Uryasev. “Asset/Liability management for pension funds using CVaR constraints.” J. Risk Finance 3 (2001): 57–71. [Google Scholar] [CrossRef]
- H. Jin, and X.Y. Zhou. “Behavioral portfolio selection in continuous time.” Math. Finance 18 (2008): 385–426. [Google Scholar] [CrossRef]
- A. Tversky, and D. Kahneman. “Advances in prospect theory: Cumulative representation of uncertainty.” J. Risk Uncertain. 5 (1992): 297–323. [Google Scholar] [CrossRef]
- M. Ammann. “Return guarantees and portfolio allocation of pension funds.” Financ. Mark. Portf. Manag. 17 (2003): 277–283. [Google Scholar] [CrossRef]
- J.D. Azzato, and J.B. Krawczyk. “Applying a finite-horizon numerical optimization method to a periodic optimal control problem.” Automatica 44 (2008): 1642–1651. [Google Scholar] [CrossRef] [Green Version]
- A. Windsor, and J.B. Krawczyk. “A MATLAB Package for Approximating the Solution to a Continuous-Time Stochastic Optimal Control Problem.” 1997. Available online: http://papers.ssrn.com/soL3/papers.cfm?abstract-id=73968 (accessed on 18 August 2015).
- P.A. Samuelson. “Lifetime portfolio selection by dynamic stochastic programming.” Rev. Econ. Stat. 51 (1969): 239–246. [Google Scholar] [CrossRef]
- P.E. Kloeden, and E. Platen. Numerical Solution of Stochastic Differential Equations. Berlin, Germany: Springer-Verlag, 1992. [Google Scholar]
- 1(1) When the mass of the distribution is concentrated on the left and the right tail is longer, the distribution is said right- or positively skewed; (2) when the mass of the distribution is concentrated on the right the left tail is longer, the distribution is said left- or negatively skewed.
- 2Interestingly, in the context of static portfolio management, [8] also question the wisdom of “traditional optimisation" for some investors, leverage-averse in their case.
- 3Exceptions to this include [9], [10]. The work done on the distribution builder in the first, enables subjects to build their desired pension distribution subject to a budget constraint. However, the results lead to distributions that are right skewed, which could be due to the setting of a (low) reference point at the amount guaranteed by the risk-free asset. In [10], quantiles are proposed as an effective way to evaluate the success and failings of a portfolio.
- 4Finding analytic solutions to the resulting PDEs would be a substantive research project which may not yield any results as the study subject are nonlinear PDEs. A “semi" analytic solution could be obtained by a functional expansion. We pursue numerical solutions in this paper, which are reliable and easy to interpret for parameter-specific problems.
- 5Notwithstanding the obtained solution’s parameter-specificity, our analysis can be extended to other cases through the use of specialised software (see [12]).
- 7This will be a synthetic aggregate good if there are many risky assets.
- 8Constraint (3) means no short selling or borrowing. This restriction has been weakened in the literature; however, it may be reasonable to keep it in a situation of a pension fund investor.
- 9A study of the impact of management incentives on investment strategies performed in [17] reports that maximising management revenue from fees changes little the investment strategies.
- 10An argument for using as control instead of can be found in [21]. If – the “fast" control – is Lebesgue measurable, Proposition 3.2 in that publication establishes that a solution to a differential equation which contains , but not , can be approximated by a solution obtained from an equation where is introduced as in (4).
- 11This publication deals with portfolio choice models for both pension funds and life assurance companies on a macro scale i.e., where many investors contribute to the fund. In that sense, our one-pension management problem is micro.
- 12Other constraints could be added, e.g., .
- 13This measure (7) was also used in, among others, [16], [13] and [17]. A loss-averse utility function that is concave on each side of the reference point (so, “similar" to (7)) was proposed in [22]. However, for the original parameters adopted by [22], that function is only “lightly” concave and did not generate left-skewed distributions, see [15].
- 14These authors solved the problem by splitting it into subproblems and found that the optimal strategy is one in which the investor takes on aggressive gambling strategies. The strategies computed in [23] and [24] still generate right skewed distributions, which we deem not preferable by pension fund investors.
- 15The problem with an analytical solution is that the as long as α in the utility measure (7) is just any number greater than 1, little can be said about a closed-form strategies and value functions. This is because t and x in (as in (18)) for the boundary problem with appear non-separable. Nevertheless, even if were obtained in an analytical form, a closed-form for the payoff-density function would still be an open problem. We also note that closed-form solutions in [22] were obtained for a similar but non-identical, utility function. More importantly their independent variable is not the current (observable) wealth but state price density.
- 17The skewness coefficient is calculated as . It provides a measure of asymmetry in the distribution.
- 19We can see in [11] that is never zero for less volatile risky assets.
© 2015 by the author; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Krawczyk, J.B. Delivering Left-Skewed Portfolio Payoff Distributions in the Presence of Transaction Costs. Risks 2015, 3, 318-337. https://doi.org/10.3390/risks3030318
Krawczyk JB. Delivering Left-Skewed Portfolio Payoff Distributions in the Presence of Transaction Costs. Risks. 2015; 3(3):318-337. https://doi.org/10.3390/risks3030318
Chicago/Turabian StyleKrawczyk, Jacek B. 2015. "Delivering Left-Skewed Portfolio Payoff Distributions in the Presence of Transaction Costs" Risks 3, no. 3: 318-337. https://doi.org/10.3390/risks3030318