Eigenloss: Combined PCA-Based Loss Function for Polyp Segmentation
Abstract
:1. Introduction
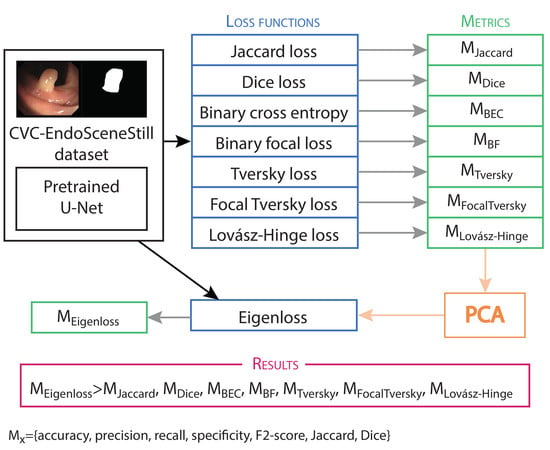
2. Materials and Methods
2.1. Dataset
2.2. Architectures and Training Parameters
2.3. Loss functions
- , or true positives (TP): polyp pixels in the ground truth binary mask that are correctly classified as polyp in the predicted binary mask.
- , or false negatives (FN): polyp pixels in the ground truth binary mask that are incorrectly classified as background in the predicted binary mask.
- , or false positives (FP): background pixels in the ground truth binary mask that are incorrectly classified as polyp in the predicted binary mask.
- , or true negatives (TN): background pixels in the ground truth binary mask that are correctly classified as background in the predicted binary mask.
2.3.1. Jaccard Loss
2.3.2. Dice Loss
2.3.3. Binary Cross Entropy Loss
2.3.4. Binary Focal Loss
2.3.5. Tversky Loss
2.3.6. Focal Tversky Loss
2.3.7. Lovász-Hinge Loss
2.4. Metrics
2.5. PCA Analysis
3. Results and Analysis
3.1. PCA Analysis
- Sum: where all coefficients are equal to 1.
- Mean: where all coefficients are equal to .
- Normalized eigenloss: where coefficients are normalized using the formula.with
3.2. Training and Testing Analysis
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- International Agency for Research on Cancer. World Cancer Report 2020; Wild, C.P., Weiderpass, E., Stewart, B.W., Eds.; International Agency for Research on Cancer: Lyon, France, 2020; ISBN 9789283204299. [Google Scholar]
- International Agency for Research on Cancer. Colorectal Cancer Factsheet; International Agency for Research on Cancer: Lyon, France, 2018. [Google Scholar]
- Siegel, R.L.; Miller, K.D.; Jemal, A. Cancer statistics, 2020. CA Cancer J. Clin. 2020, 70, 7–30. [Google Scholar] [CrossRef]
- Carioli, G.; Bertuccio, P.; Boffetta, P.; Levi, F.; La Vecchia, C.; Negri, E.; Malvezzi, M. European cancer mortality predictions for the year 2020 with a focus on prostate cancer. Ann. Oncol. 2020, 31, 650–658. [Google Scholar] [CrossRef] [PubMed]
- Digestive Cancers Europe. Colorectal Screening in Europe Saving Lives and Saving Money; Digestive Cancers Europe: Brussles, Belgium, 2019; Available online: https://www.digestivecancers.eu/wp-content/uploads/2020/02/466-Document-DiCEWhitePaper2019.pdf (accessed on 1 August 2020).
- Byrne, M.F.; Shahidi, N.; Rex, D.K. Will Computer-Aided Detection and Diagnosis Revolutionize Colonoscopy? Gastroenterology 2017, 153, 1460–1464.e1. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chen, Y.-W.; Jain, L.C. (Eds.) Deep Learning in Healthcare; Intelligent Systems Reference Library; Springer International Publishing: Cham, Switzerland, 2020; Volume 171, ISBN 978-3-030-32605-0. [Google Scholar]
- Tajbakhsh, N.; Jeyaseelan, L.; Li, Q.; Chiang, J.N.; Wu, Z.; Ding, X. Embracing Imperfect Datasets: A Review of Deep Learning Solutions for Medical Image Segmentation. Med. Image Anal. 2020, 63, 101693. [Google Scholar] [CrossRef] [Green Version]
- Nagendran, M.; Chen, Y.; Lovejoy, C.A.; Gordon, A.C.; Komorowski, M.; Harvey, H.; Topol, E.J.; Ioannidis, J.P.A.; Collins, G.S.; Maruthappu, M. Artificial intelligence versus clinicians: Systematic review of design, reporting standards, and claims of deep learning studies in medical imaging. BMJ 2020, 368, 1–12. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Liu, X.; Faes, L.; Kale, A.U.; Wagner, S.K.; Fu, D.J.; Bruynseels, A.; Mahendiran, T.; Moraes, G.; Shamdas, M.; Kern, C.; et al. A comparison of deep learning performance against health-care professionals in detecting diseases from medical imaging: A systematic review and meta-analysis. Lancet Digit. Health 2019, 1, e271–e297. [Google Scholar] [CrossRef]
- E Gonçalves, W.G.; dos Santos, M.H.D.P.; Lobato, F.M.F.; Ribeiro-dos-Santos, Â.; de Araújo, G.S. De Deep learning in gastric tissue diseases: A systematic review. BMJ Open Gastroenterol. 2020, 7, e000371. [Google Scholar] [CrossRef] [Green Version]
- Soffer, S.; Klang, E.; Shimon, O.; Nachmias, N.; Eliakim, R.; Ben-Horin, S.; Kopylov, U.; Barash, Y. Deep learning for wireless capsule endoscopy: A systematic review and meta-analysis. Gastrointest. Endosc. 2020. [Google Scholar] [CrossRef]
- Iwahori, Y.; Hagi, H.; Usami, H.; Woodham, R.J.; Wang, A.; Bhuyan, M.K.; Kasugai, K. Automatic polyp detection from endoscope image using likelihood map based on edge information. In ICPRAM 2017—Proceedings 6th International Conference Pattern Recognit, Porto, Portugal, 24-26 February 2017; SciTePress: Setubal, Portugal, 26 February; pp. 402–409. [CrossRef]
- Iakovidis, D.K.; Maroulis, D.E.; Karkanis, S.A. An intelligent system for automatic detection of gastrointestinal adenomas in video endoscopy. Comput. Biol. Med. 2006, 36, 1084–1103. [Google Scholar] [CrossRef]
- Ameling, S.; Wirth, S.; Paulus, D.; Lacey, G.; Vilarino, F. Texture-based polyp detection in colonoscopy. In Proceedings of the Bildverarbeitung für die Medizin 2009, Heidelberg, Germany, 22–25 March 2009; pp. 346–350. [Google Scholar]
- Bernal, J.; Sánchez, F.J.; Fernández-Esparrach, G.; Gil, D.; Rodríguez de Miguel, C.; Vilariño, F. WM-DOVA maps for accurate polyp highlighting in colonoscopy: Validation vs. saliency maps from physicians. Comput. Med. Imaging Graph. 2015, 43, 99–111. [Google Scholar] [CrossRef]
- Bernal, J.; Sánchez, F.J.; Vilariño, F. Towards automatic polyp detection with a polyp appearance model. Pattern Recognit. 2012, 45, 3166–3182. [Google Scholar] [CrossRef]
- Minaee, S.; Wang, Y. An ADMM Approach to Masked Signal Decomposition Using Subspace Representation. IEEE Trans. Image Process. 2019, 28, 3192–3204. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Li, J.; Bioucas-Dias, J.M.; Plaza, A. Semisupervised hyperspectral image segmentation using multinomial logistic regression with active learning. IEEE Trans. Geosci. Remote Sens. 2010, 48, 4085–4098. [Google Scholar] [CrossRef] [Green Version]
- Lui, T.K.; Hui, C.K.; Tsui, V.W.; Cheung, K.S.; Ko, M.K.; aCC Foo, D.; Mak, L.Y.; Yeung, C.K.; Lui, T.H.; Wong, S.Y.; et al. New insights on missed colonic lesions during colonoscopy through artificial intelligence–assisted real-time detection (with video). Gastrointest. Endosc. 2020. [Google Scholar] [CrossRef] [PubMed]
- Bernal, J.; Tajbakhsh, N.; Sánchez, F.J.; Matuszewski, B.J.; Chen, H.; Yu, L.; Angermann, Q.; Romain, O.; Rustad, B.; Balasingham, I.; et al. Comparative Validation of Polyp Detection Methods in Video Colonoscopy: Results from the MICCAI 2015 Endoscopic Vision Challenge. IEEE Trans. Med. Imaging 2017, 36, 1231–1249. [Google Scholar] [CrossRef] [PubMed]
- Sánchez-Peralta, L.F.; Bote-Curiel, L.; Picon, A.; Sánchez-Margallo, F.M.; Pagador, J.B. Deep learning to find colorectal polyps in colonoscopy: A systematic literature review. Artif. Intell. Med. 2020, in press. [Google Scholar] [CrossRef]
- Minaee, S.; Boykov, Y.; Porikli, F.; Plaza, A.; Kehtarnavaz, N.; Terzopoulos, D. Image Segmentation Using Deep Learning: A Survey. arXiv 2020, arXiv:2001.05566. [Google Scholar]
- Ronneberger, O.; Fischer, P.; Brox, T. U-Net: Convolutional Networks for Biomedical Image Segmentation. In Medical Image Computing and Computer-Assisted Intervention—MICCAI 2015; Lecture Notes in Computer Science, vol 9351; Navab, N., Hornegger, J., Wells, W.M., Frangi, A.F., Eds.; Springer: Berlin/Heidelberg, Germany, 2015; pp. 234–241. ISBN 9783319245737. [Google Scholar]
- Milletari, F.; Navab, N.; Ahmadi, S. V-Net: Fully Convolutional Neural Networks for Volumetric Medical Image Segmentation. In Proceedings of the 2016 Fourth International Conference on 3D Vision (3DV), Stanford, CA, USA, 25–28 October 2016; pp. 565–571. [Google Scholar] [CrossRef] [Green Version]
- Zhou, Z.; Siddiquee, M.M.R.; Tajbakhsh, N.; Liang, J. UNet++: A Nested U-Net Architecture for Medical Image Segmentation. In Deep Learning in Medical Image Analysis and Multimodal Learning for Clinical Decision Support; DLMIA 2018, ML-CDS 2018; Lecture Notes in Computer Science; Springer: Cham, Switzerland, 2018; Volume 11045, ISBN 1424400430. [Google Scholar]
- Zahangir Alom, M.; Yakopcic, C.; Taha, T.M.; Asari, V.K. Nuclei Segmentation with Recurrent Residual Convolutional Neural Networks based U-Net (R2U-Net). In Proceedings of the NAECON 2018-IEEE National Aerospace and Electronics Conference, Dayton, OH, USA, 23–26 July 2018; pp. 228–233. [Google Scholar] [CrossRef]
- Isensee, F.; Petersen, J.; Klein, A.; Zimmerer, D.; Jaeger, P.F.; Kohl, S.; Wasserthal, J.; Koehler, G.; Norajitra, T.; Wirkert, S.; et al. nnU-Net: Self-adapting Framework for U-Net-Based Medical Image Segmentation. Inform. Aktuell 2019, 22. [Google Scholar] [CrossRef] [Green Version]
- Chaurasia, A.; Culurciello, E. LinkNet: Exploiting encoder representations for efficient semantic segmentation. In Proceedings of the 2017 IEEE Visual Communications and Image Processing (VCIP), St. Petersburg, FL, USA, 10–13 December 2018. [Google Scholar] [CrossRef] [Green Version]
- Rezaei, S.; Emami, A.; Zarrabi, H.; Rafiei, S.; Najarian, K.; Karimi, N.; Samavi, S.; Reza Soroushmehr, S.M. Gland Segmentation in Histopathology Images Using Deep Networks and Handcrafted Features. In Proceedings of the 2019 41st Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Berlin, Germany, 23–27 July 2019; pp. 1031–1034. [Google Scholar] [CrossRef] [Green Version]
- Lee, J.Y.; Islam, M.; Woh, J.R.; Washeem, T.S.M.; Ngoh, L.Y.C.; Wong, W.K.; Ren, H. Ultrasound needle segmentation and trajectory prediction using excitation network. Int. J. Comput. Assist. Radiol. Surg. 2020, 15, 437–443. [Google Scholar] [CrossRef]
- Bagheri, M.; Mohrekesh, M.; Tehrani, M.; Najarian, K.; Karimi, N.; Samavi, S.; Reza Soroushmehr, S.M. Deep Neural Network based Polyp Segmentation in Colonoscopy Images using a Combination of Color Spaces. In Proceedings of the 2019 41st Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Berlin, Germany, 23–27 July 2019; pp. 6742–6745. [Google Scholar] [CrossRef]
- Garcia-Pedrero, A.; García-Cervigón, A.I.; Olano, J.M.; García-Hidalgo, M.; Lillo-Saavedra, M.; Gonzalo-Martín, C.; Caetano, C.; Calderón-Ramírez, S. Convolutional neural networks for segmenting xylem vessels in stained cross-sectional images. Neural Comput. Appl. 2019, 6. [Google Scholar] [CrossRef]
- Shvets, A.A.; Rakhlin, A.; Kalinin, A.A.; Iglovikov, V.I. Automatic Instrument Segmentation in Robot-Assisted Surgery using Deep Learning. In Proceedings of the 2018 17th IEEE International Conference on Machine Learning and Applications (ICMLA), Orlando, FL, USA, 17–20 December 2019; pp. 624–628. [Google Scholar] [CrossRef] [Green Version]
- Kholiavchenko, M.; Sirazitdinov, I.; Kubrak, K.; Badrutdinova, R.; Kuleev, R.; Yuan, Y.; Vrtovec, T.; Ibragimov, B. Contour-aware multi-label chest X-ray organ segmentation. Int. J. Comput. Assist. Radiol. Surg. 2020, 15, 425–436. [Google Scholar] [CrossRef] [PubMed]
- Singh, J.; Tripathy, A.; Garg, P.; Kumar, A. Lung tuberculosis detection using anti-aliased convolutional networks. Procedia Comput. Sci. 2020, 173, 281–290. [Google Scholar] [CrossRef]
- Wichakam, I.; Panboonyuen, T.; Udomcharoenchaikit, C. Real-Time Polyps Segmentation for Colonoscopy Video Frames Using Compressed Fully Convolutional Network. In International Conference on Multimedia Modeling; Lecture Notes in Computer Science, vol 10704; Springer: Cham, Switzerlan, 2018; pp. 393–404. ISBN 978-3-319-51813-8. [Google Scholar]
- Simonyan, K.; Zisserman, A. Very Deep Convolutional Networks for Large-Scale Image Recognition. arXiv 2015, arXiv:1409.1556. [Google Scholar] [CrossRef] [Green Version]
- Vázquez, D.; Bernal, J.; Sánchez, F.J.; Fernández-Esparrach, G.; López, A.M.; Romero, A.; Drozdzal, M.; Courville, A. A Benchmark for Endoluminal Scene Segmentation of Colonoscopy Images. J. Healthc. Eng. 2017. [Google Scholar] [CrossRef]
- Long, J.; Shelhamer, E.; Darrell, T. Fully convolutional networks for semantic segmentation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 3431–3440. [Google Scholar]
- Wickstrøm, K.; Kampffmeyer, M.; Jenssen, R. Uncertainty modeling and interpretability in convolutional neural networks for polyp segmentation. In Proceedings of the 2018 IEEE International Workshop on Machine Learning for Signal Processing, Aalborg, Denmark, 17–20 September 2018. [Google Scholar]
- Jolliffe, I.T. Principal Components Analysis; Springer: New York, NY, USA, 2002; ISBN 978-0-387-22440-4. [Google Scholar]
- Ansari, K.; Krebs, A.; Benezeth, Y.; Marzani, F. Color Converting of Endoscopic Images Using Decomposition Theory and Principal Component Analysis. In Proceedings of the 9th International Conference on Computer Science, Engineering and Applications, Toronto, ON, Canada, 13–14 July 2019; pp. 151–159. [Google Scholar] [CrossRef]
- Shao, X.; Zheng, W.; Huang, Z. Near-infrared autofluorescence spectroscopy for in vivo identification of hyperplastic and adenomatous polyps in the colon. Biosens. Bioelectron. 2011, 30, 118–122. [Google Scholar] [CrossRef]
- Kim, Y.; Kim, H.G.; Hyeon, J.; Choi, H.J. Clinical opinions generation from general blood test results using deep neural network with principle component analysis and regularization. In Proceedings of the 2017 IEEE International Conference on Big Data and Smart Computing (BigComp), Jeju, Korea, 13–16 February 2017; pp. 386–389. [Google Scholar] [CrossRef]
- Sánchez-González, A.; García-Zapirain, B.; Sierra-Sosa, D.; Elmaghraby, A. Automatized colon polyp segmentation via contour region analysis. Comput. Biol. Med. 2018, 100, 152–164. [Google Scholar] [CrossRef]
- Cho, K.; Roh, J.H.; Kim, Y.; Cho, S. A Performance Comparison of Loss Functions. In Proceedings of the 2019 International Conference on Information and Communication Technology Convergence (ICTC), Jeju Island, Korea, 16–18 October 2019; pp. 1146–1151. [Google Scholar] [CrossRef]
- Keren, G.; Sabato, S.; Schuller, B. Analysis of loss functions for fast single-class classification. Knowl. Inf. Syst. 2020, 62, 337–358. [Google Scholar] [CrossRef]
- Ghodrati, V.; Shao, J.; Bydder, M.; Zhou, Z.; Yin, W.; Nguyen, K.L.; Yang, Y.; Hu, P. MR image reconstruction using deep learning: Evaluation of network structure and loss functions. Quant. Imaging Med. Surg. 2019, 9, 1516–1527. [Google Scholar] [CrossRef]
- Kim, B.; Han, M.; Shim, H.; Baek, J. A performance comparison of convolutional neural network-based image denoising methods: The effect of loss functions on low-dose CT images. Med. Phys. 2019, 46, 3906–3923. [Google Scholar] [CrossRef]
- Pathak, A.; Maheshwari, R. Comparative analysis of different loss functions for deep face recognition. In Proceedings of the 2019 2nd International Conference on Algorithms, Computing and Artificial Intelligence, Sanya, China, 20–22 December 2019; pp. 390–397. [Google Scholar] [CrossRef]
- Sukhbaatar, S.; Bruna, J.; Paluri, M.; Bourdev, L.; Fergus, R. Training convolutional networks with noisy labels. arXiv 2014, arXiv:1406.2080. [Google Scholar]
- Lin, T.-Y.; Goyal, P.; Girshick, R.; He, K.; Dollar, P. Focal Loss for Dense Object Detection. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 2999–3007. [Google Scholar] [CrossRef] [Green Version]
- Rahman, M.A.; Wang, Y. Optimizing intersection-over-union in deep neural networks for image segmentation. In International Symposium on Visual Computing; 10072 LNCS; Springer: Cham, Switzerland, 2016; pp. 234–244. [Google Scholar] [CrossRef]
- Salehi, S.S.M.; Erdogmus, D.; Gholipour, A. Tversky loss function for image segmentation using 3D fully convolutional deep networks. In International Workshop on Machine Learning in Medical Imaging; 10541 LNCS; Springer: Cham, Switzerland, 2017; pp. 379–387. [Google Scholar] [CrossRef] [Green Version]
- Berman, M.; Triki, A.R.; Blaschko, M.B. The Lovasz-Softmax Loss: A Tractable Surrogate for the Optimization of the Intersection-Over-Union Measure in Neural Networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 4413–4421. [Google Scholar] [CrossRef] [Green Version]
- Abraham, N.; Khan, N.M. A novel focal tversky loss function with improved attention u-net for lesion segmentation. In Proceedings of the 2019 IEEE 16th International Symposium on Biomedical Imaging (ISBI 2019), Venice, Italy, 8–11 April 2019; pp. 683–687. [Google Scholar] [CrossRef] [Green Version]
- Kervadec, H.; Bouchtiba, J.; Desrosiers, C.; Granger, É.; Dolz, J.; Ayed, I. Ben Boundary loss for highly unbalanced segmentation. In Proceedings of the International Conference on Medical Imaging with Deep Learning, London, UK, 8–10 July 2019; pp. 285–296. [Google Scholar]
- Karimi, D.; Salcudean, S.E. Reducing the Hausdorff Distance in Medical Image Segmentation with Convolutional Neural Networks. IEEE Trans. Med. Imaging 2020, 39, 499–513. [Google Scholar] [CrossRef] [Green Version]
- Asgari Taghanaki, S.; Abhishek, K.; Cohen, J.P.; Cohen-Adad, J.; Hamarneh, G. Deep Semantic Segmentation of Natural and Medical Images: A Review; Springer: Cham, The Netherlands, 2020; ISBN 0123456789. [Google Scholar]
- Hajiabadi, H.; Babaiyan, V.; Zabihzadeh, D.; Hajiabadi, M. Combination of loss functions for robust breast cancer prediction. Comput. Electr. Eng. 2020, 84, 106624. [Google Scholar] [CrossRef]
- Wang, B.; Lei, Y.; Tian, S.; Wang, T.; Liu, Y.; Patel, P.; Ashesh, B.; Mao, H.; Curran, W.J.; Liu, T.; et al. Deeply Supervised 3D FCN with Group Dilated Convolution for Automatic MRI Prostate Segmentation. Med. Phys. 2019, 46, 1707–1718. [Google Scholar] [CrossRef] [PubMed]
- Oksuz, I.; Clough, J.; Ruijsink, B.; Puyol-Antón, E.; Gastao Cruz, K.; Prieto, C.; King, A.P.; Schnabel, J.A. High-quality segmentation of low quality cardiac MR images using k-space artefact correction. In Proceedings of the International Conference on Medical Imaging with Deep Learning, London, UK, 8–10 July 2019; Volume 102, pp. 380–389. [Google Scholar]
- Mohammed, A.; Yildirim, S.; Farup, I.; Pedersen, M.; Hovde, Ø. Y-Net: A deep Convolutional Neural Network for Polyp Detection. arXiv 2018, arXiv:1806.01907. [Google Scholar]
- Huang, G.; Liu, Z.; van der Maaten, L.; Weinberger, K.Q. Densely Connected Convolutional Networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018. [Google Scholar] [CrossRef] [Green Version]
- Stanford Vision Lab. Stanford University. Princeton University ImageNet. Available online: http://www.image-net.org/ (accessed on 10 February 2020).
- Yakubovskiy, P. Segmentation Models. 2019. Available online: https://segmentation-models.readthedocs.io/en/latest/index.html (accessed on 1 August 2020).
- Chollet, F. Keras. Available online: https://github.com/keras-team/keras (accessed on 10 February 2020).
- Abadi, M.; Agarwal, A.; Barham, P.; Brevdo, E.; Chen, Z.; Citro, C.; Corrado, G.S.; Davis, A.; Dean, J.; Devin, M.; et al. TensorFlow: Large-Scale Machine Learning on Heterogeneous Distributed Systems. arXiv 2016, arXiv:1603.04467. [Google Scholar]
- García-Gómez, J.M.; Tortajada, S. Definition of Loss Functions for Learning from Imbalanced Data to Minimize Evaluation metrics. In Data Mining in Clinical Medicine; Fernández-Llatas, C., García-Gómez, J.M., Eds.; Humana Press: New York, NY, USA, 2015; pp. 19–37. [Google Scholar]
- Jaccard, P. The distribution of the flora in the alpine zone. New Phytol. 1912, 11, 37–50. [Google Scholar] [CrossRef]
- Dice, L.R. Measures of the Amount of Ecologic Association Between Species. Ecology 1945, 26, 297–302. [Google Scholar] [CrossRef]
- Goodfellow, I.; Bengio, Y.; Courville, A. Deep Learning; MIT Press: Cambridge, MA, USA, 2016. [Google Scholar]
- Tversky, A. Features of similarity. Psychol. Rev. 1977, 84, 327–352. [Google Scholar] [CrossRef]
- Cliff, N. The Eigenvalues-Greater-Than-One Rule and the Reliability of Components. Psychol. Bull. 1988, 103, 276–279. [Google Scholar] [CrossRef]
- Maier-Hein, L.; Eisenmann, M.; Reinke, A.; Onogur, S.; Stankovic, M.; Scholz, P.; Arbel, T.; Bogunovic, H.; Bradley, A.P.; Carass, A.; et al. Why rankings of biomedical image analysis competitions should be interpreted with care. Nat. Commun. 2018, 9, 5217. [Google Scholar] [CrossRef] [Green Version]
- Taha, A.A.; Hanbury, A. Metrics for evaluating 3D medical image segmentation: Analysis, selection, and tool. BMC Med. Imaging 2015, 15. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Qin, Z.; Zhang, Z.; Li, Y.; Guo, J. Making Deep Neural Networks Robust to Label Noise: Cross-Training with a Novel Loss Function. IEEE Access 2019, 7, 130893–130902. [Google Scholar] [CrossRef]
- Guo, S.; Li, T.; Zhang, C.; Li, N.; Kang, H.; Wang, K. Random Drop Loss for Tiny Object Segmentation: Application to Lesion Segmentation in Fundus Images. In International Conference on Artificial Neural Networks; Springer: Cham, Switzerland, 2019; pp. 213–224. [Google Scholar]
- Asaturyan, H.; Thomas, E.L.; Fitzpatrick, J.; Bell, J.D.; Villarini, B. Advancing Pancreas Segmentation in Multi-protocol MRI Volumes Using Hausdorff-Sine Loss Function. In International Workshop on Machine Learning in Medical Imaging; Springer: Cham, Switzerland, 2019; Volume 11861 LNCS, pp. 27–35. [Google Scholar]
- Maharjan, S.; Alsadoon, A.; Prasad, P.W.C.; Al-Dalain, T.; Alsadoon, O.H. A novel enhanced softmax loss function for brain tumour detection using deep learning. J. Neurosci. Methods 2020, 330, 108520. [Google Scholar] [CrossRef] [PubMed]
- Iglovikov, V.; Shvets, A. TernausNet: U-Net with VGG11 Encoder Pre-Trained on ImageNet for Image Segmentation. arXiv 2018, arXiv:1801.05746. [Google Scholar]
- Narayanan, B.N.; Hardie, R.C. A Computationally Efficient U-Net Architecture for Lung Segmentation in Chest Radiographs. In Proceedings of the 2019 IEEE National Aerospace and Electronics Conference (NAECON), Dayton, OH, USA, 15–19 July 2019; pp. 279–284. [Google Scholar] [CrossRef]
- Chen, L.-C.; Papandreou, G.; Kokkinos, I.; Murphy, K.; Yuille, A.L. DeepLab: Semantic Image Segmentation with Deep Convolutional Nets, Atrous Convolution, and Fully Connected CRFs. arXiv 2016, arXiv:1606.00915. [Google Scholar] [CrossRef]
- Huang, Z.; Wang, X.; Huang, L.; Huang, C.; Wei, Y.; Liu, W. CCNet: Criss-cross attention for semantic segmentation. In Proceedings of the IEEE International Conference on Computer Vision, Seoul, Korea, 27 October–3 November 2019; pp. 603–612. [Google Scholar] [CrossRef] [Green Version]





| Loss Function | Accuracy | Precision | Recall | Specificity | F2-Score | Jaccard | Dice |
|---|---|---|---|---|---|---|---|
| Jaccard | 93.36 ± 10.26 | 88.69 ± 23.02 | 65.65 ± 37.52 | 99.24 ± 1.73 | 65.79 ± 36.20 | 59.77 ± 35.03 | 67.39 ± 34.44 |
| Dice | 92.76 ± 10.45 | 82.20 ± 27.36 | 63.24 ± 37.94 | 99.07 ± 1.66 | 63.23 ± 36.42 | 56.38 ± 34.59 | 64.61 ± 34.47 |
| Binary entropy | 93.18 ± 10.28 | 85.39 ± 30.95 | 64.62 ± 38.92 | 99.29 ± 1.45 | 64.89 ± 37.90 | 59.48 ± 36.35 | 66.39 ± 36.58 |
| Binary focal | 93.34 ± 10.28 | 82.44 ± 26.45 | 68.84 ± 36.37 | 98.59 ± 2.84 | 68.13 ± 34.91 | 60.49 ± 33.66 | 68.48 ± 33.59 |
| Tversky | 92.80 ± 10.53 | 82.80 ± 29.18 | 60.84 ± 39.16 | 99.22 ± 1.57 | 61.20 ± 38.03 | 55.34 ± 36.12 | 62.88 ± 36.59 |
| Focal Tversky | 93.10 ± 9.94 | 81.19 ± 26.54 | 64.03 ± 38.72 | 98.98 ± 2.13 | 63.81 ± 37.25 | 57.20 ± 35.57 | 64.89 ± 35.46 |
| Lovász-Hinge | 91.26 ± 11.07 | 72.26 ± 41.71 | 40.09 ± 39.55 | 99.71 ± 0.86 | 41.48 ± 39.44 | 38.23 ± 37.64 | 44.74 ± 39.49 |
| Sum | 92.78 ± 10.45 | 81.15 ± 32.97 | 57.76 ± 39.88 | 99.37 ± 1.44 | 58.43 ± 39.01 | 53.58 ± 37.44 | 60.64 ± 38.11 |
| Mean | 93.33 ± 10.5 | 84.07 ± 29.03 | 69.53 ± 35.64 | 98.84 ± 2.42 | 69.38 ± 34.42 | 62.83 ± 33.45 | 70.49 ± 33.13 |
| Eigenloss | 93.00 ± 10.91 | 80.31 ± 31.35 | 65.07 ± 37.70 | 99.00 ± 2.25 | 65.45 ± 36.70 | 59.66 ± 35.32 | 67.04 ± 35.39 |
| Norm Eigenloss | 92.97 ± 10.13 | 81.62 ± 27.02 | 64.02 ± 37.73 | 98.91 ± 2.06 | 63.82 ± 35.99 | 56.56 ± 33.99 | 65.01 ± 33.99 |
| Loss Function | Accuracy | Precision | Recall | Specificity | F2-Score | Jaccard | Dice |
|---|---|---|---|---|---|---|---|
| Jaccard | 95.02 ± 9.53 | 86.95 ± 23.58 | 79.18 ± 33.08 | 99.14 ± 1.66 | 78.56 ± 31.94 | 72.17 ± 31.06 | 78.45 ± 30.37 |
| Dice | 94.17 ± 10.22 | 90.10 ± 24.86 | 77.88 ± 33.74 | 98.99 ± 2.34 | 76.63 ± 32.63 | 69.88 ± 32.63 | 76.30 ± 31.61 |
| Binary entropy | 94.30 ± 9.68 | 86.58 ± 23.06 | 75.60 ± 33.75 | 99.12 ± 1.65 | 74.96 ± 32.17 | 68.07 ± 31.89 | 75.39 ± 30.06 |
| Binary focal | 94.27 ± 9.81 | 84.61 ± 22.94 | 80.84 ± 31.62 | 98.64 ± 2.67 | 78.69 ± 30.03 | 70.01 ± 30.18 | 77.40 ± 28.41 |
| Tversky | 94.74 ± 9.77 | 89.04 ± 19.81 | 81.04 ± 30.35 | 99.02 ± 2.29 | 79.71 ± 29.35 | 73.19 ± 30.17 | 79.72 ± 27.98 |
| Focal Tversky | 94.19 ± 9.83 | 83.08 ± 25.12 | 78.59 ± 34.18 | 98.62 ± 2.90 | 68.05 ± 32.22 | 75.10 ± 31.24 | 79.84 ± 24.73 |
| Lovász-Hinge | 94.73 ± 9.77 | 87.52 ± 21.59 | 80.07 ± 31.72 | 98.95 ± 2.37 | 79.01 ± 30.42 | 72.26 ± 30.62 | 78.86 ± 28.78 |
| Sum | 94.76 ± 9.53 | 87.92 ± 22.08 | 80.72 ± 30.32 | 98.95 ± 2.38 | 79.69 ± 29.12 | 72.89 ± 29.77 | 79.62 ± 27.80 |
| Mean | 94.45 ± 9.77 | 86.12 ± 22.40 | 80.45 ± 31.49 | 98.82 ± 2.56 | 78.48 ± 30.17 | 70.75 ± 30.84 | 77.72 ± 28.96 |
| Eigenloss | 94.43 ± 9.78 | 89.83 ± 21.63 | 77.39 ± 33.28 | 99.06 ± 2.18 | 76.41 ± 31.97 | 69.35 ± 31.55 | 76.33 ± 30.39 |
| Norm Eigenloss | 94.68 ± 9.69 | 87.85 ± 22.12 | 79.24 ± 32.31 | 99.09 ± 1.95 | 78.43 ± 31.11 | 71.86 ± 31.02 | 78.37 ± 29.60 |
| Loss Function | Accuracy | Precision | Recall | Specificity | F2-Score | Jaccard | Dice |
|---|---|---|---|---|---|---|---|
| Jaccard | 93.41 ± 10.47 | 82.86 ± 30.16 | 68.2 ± 36.67 | 99.34 ± 1.22 | 68.51 ± 35.56 | 62.75 ± 34.19 | 70.07 ± 34.11 |
| Dice | 93.59 ± 10.38 | 81.03 ± 32.94 | 67.58 ± 38.01 | 99.49 ± 0.96 | 67.90 ± 37.10 | 62.53 ± 35.45 | 69.24 ± 35.92 |
| Binary entropy | 93.61 ± 9.98 | 83.01 ± 26.67 | 70.18 ± 35.97 | 98.97 ± 1.97 | 69.76 ± 34.50 | 62.65 ± 33.05 | 70.48 ± 32.88 |
| Binary focal | 93.15 ± 10.28 | 81.04 ± 28.02 | 66.18 ± 38.02 | 98.95 ± 1.76 | 65.63 ± 36.44 | 58.36 ± 34.85 | 66.22 ± 34.65 |
| Tversky | 93.45 ± 10.78 | 82.54 ± 28.10 | 69.82 ± 37.05 | 99.13 ± 1.85 | 69.55 ± 35.85 | 63.14 ± 34.49 | 70.27 ± 34.33 |
| Focal Tversky | 93.56 ± 10.35 | 83.56 ± 26.75 | 70.18 ± 37.39 | 99.09 ± 1.74 | 69.54 ± 36.10 | 62.81 ± 34.66 | 69.91 ± 34.58 |
| Lovász-Hinge | 92.98 ± 10.28 | 80.57 ± 29.84 | 68.17 ± 37.82 | 98.73 ± 2.60 | 67.21 ± 36.06 | 59.6 ± 34.49 | 67.42 ± 34.23 |
| Sum | 93.26 ± 10.08 | 78.00 ± 32.57 | 68.06 ± 36.90 | 98.76 ± 2.59 | 67.53 ± 35.50 | 60.4 ± 34.20 | 68.17 ± 34.12 |
| Mean | 93.53 ± 10.36 | 84.11 ± 28.24 | 68.64 ± 37.03 | 99.35 ± 1.23 | 68.80 ± 35.79 | 62.77 ± 34.16 | 70.10 ± 34.05 |
| Eigenloss | 93.50 ± 10.60 | 83.31 ± 28.49 | 69.52 ± 36.50 | 99.28 ± 1.76 | 69.51 ± 35.31 | 63.24 ± 33.86 | 70.61 ± 33.68 |
| Norm Eigenloss | 93.12 ± 10.59 | 84.35 ± 28.65 | 65.74 ± 37.70 | 99.33 ± 1.61 | 66.13 ± 36.53 | 60.62 ± 35.21 | 67.93 ± 35.03 |
| Loss Function | Accuracy | Precision | Recall | Specificity | F2-Score | Jaccard | Dice |
|---|---|---|---|---|---|---|---|
| Jaccard | 94.71 ± 9.08 | 87.32 ± 20.08 | 81.92 ± 27.25 | 98.58 ± 3.05 | 79.84 ± 26.01 | 71.57 ± 28.02 | 79.44 ± 24.79 |
| Dice | 94.47 ± 9.90 | 86.44 ± 23.22 | 76.91 ± 34.45 | 99.19 ± 1.52 | 76.27 ± 33.16 | 69.71 ± 32.18 | 76.32 ± 31.22 |
| Binary entropy | 93.99 ± 10.18 | 84.52 ± 25.45 | 77.44 ± 34.21 | 98.70 ± 2.73 | 75.96 ± 32.98 | 68.74 ± 32.73 | 75.44 ± 31.57 |
| Binary focal | 94.39 ± 9.88 | 85.15 ± 25.81 | 77.04 ± 34.42 | 99.08 ± 2.07 | 75.99 ± 33.15 | 69.11 ± 32.62 | 75.71 ± 31.76 |
| Tversky | 94.68 ± 9.41 | 88.13 ± 21.48 | 78.47 ± 31.38 | 99.00 ± 2.37 | 77.74 ± 29.93 | 70.92 ± 30.11 | 78.12 ± 28.08 |
| Focal Tversky | 94.31 ± 9.64 | 85.96 ± 21.48 | 81.01 ± 29.48 | 98.52 ± 3.11 | 79.16 ± 27.99 | 70.84 ± 28.83 | 78.53 ± 26.54 |
| Lovász-Hinge | 94.89 ± 9.56 | 86.73 ± 22.64 | 79.62 ± 31.09 | 99.21 ± 1.29 | 79.02 ± 30.08 | 72.41 ± 29.88 | 79.13 ± 28.59 |
| Sum | 94.36 ± 9.65 | 84.13 ± 25.73 | 76.50 ± 34.19 | 99.01 ± 1.67 | 75.47 ± 32.69 | 68.36 ± 32.11 | 75.45 ± 30.70 |
| Mean | 94.11 ± 10.09 | 85.48 ± 26.24 | 74.92 ± 34.48 | 98.96 ± 2.67 | 74.17 ± 33.11 | 67.77 ± 32.82 | 74.7 ± 31.61 |
| Eigenloss | 94.59 ± 9.61 | 88.65 ± 18.25 | 80.23 ± 30.78 | 99.05 ± 1.92 | 79.18 ± 29.26 | 71.84 ± 29.25 | 79.07 ± 27.07 |
| NormEigenloss | 94.60 ± 9.86 | 87.79 ± 21.65 | 77.81 ± 32.85 | 99.16 ± 1.89 | 77.49 ± 31.66 | 71.57 ± 31.28 | 78.06 ± 29.85 |
| U-Net-VGG-16 | U-Net-Densenet121 | LinkNet-VGG-16 | LinkNet-Densenet121 | |||||
|---|---|---|---|---|---|---|---|---|
| Eigenvalue | 5.803 | 6.076 | 5.913 | 5.998 | ||||
| % Variance | 82.91 | 86.80 | 84.47 | 85.69 | ||||
| Loss function | Com. | Com. | Com. | Com. | ||||
| Jaccard | 0.875 | 0.935 | 0.819 | 0.905 | 0.843 | 0.918 | 0.819 | 0.905 |
| Dice | 0.845 | 0.919 | 0.894 | 0.946 | 0.864 | 0.930 | 0.878 | 0.937 |
| Binary cross entropy | 0.835 | 0.914 | 0.785 | 0.886 | 0.866 | 0.930 | 0.842 | 0.918 |
| Binary focal | 0.826 | 0.909 | 0.892 | 0.944 | 0.805 | 0.897 | 0.861 | 0.928 |
| Tversky | 0.881 | 0.939 | 0.906 | 0.952 | 0.842 | 0.917 | 0.881 | 0.939 |
| Focal Tversky | 0.884 | 0.940 | 0.869 | 0.932 | 0.888 | 0.942 | 0.878 | 0.937 |
| Lovász-Hinge | 0.657 | 0.811 | 0.911 | 0.954 | 0.805 | 0.897 | 0.840 | 0.916 |
| U-Net-VGG-16 | U-Net-Densenet121 | LinkNet-VGG-16 | LinkNet-Densenet121 | |||||
|---|---|---|---|---|---|---|---|---|
| Loss Function | # Epoch | Val Loss | # Epoch | Val Loss | # Epoch | Val Loss | # Epoch | Val Loss |
| Jaccard | 292 | 0.17 | 71 | 0.16 | 292 | 0.18 | 17 | 0.15 |
| Dice | 216 | 0.19 | 71 | 0.12 | 211 | 0.17 | 71 | 0.16 |
| Binary cross entropy | 292 | 0.16 | 71 | 0.15 | 292 | 0.15 | 211 | 0.14 |
| Binary focal | 198 | 0.20 | 153 | 0.19 | 292 | 0.15 | 17 | 0.16 |
| Tversky | 292 | 0.16 | 71 | 0.16 | 292 | 0.18 | 47 | 0.18 |
| Focal Tversky | 216 | 0.20 | 71 | 0.14 | 292 | 0.16 | 211 | 0.17 |
| Lovász-Hinge | 184 | 0.19 | 71 | 0.15 | 216 | 0.16 | 17 | 0.16 |
| Sum | 259 | 0.22 | 71 | 0.15 | 292 | 0.18 | 128 | 0.15 |
| Mean | 172 | 0.16 | 71 | 0.14 | 211 | 0.12 | 17 | 0.14 |
| Eigenloss | 211 | 0.19 | 114 | 0.17 | 211 | 0.14 | 17 | 0.16 |
| Normalized eigenloss | 211 | 0.20 | 71 | 0.13 | 292 | 0.16 | 17 | 0.18 |
| Work | Accuracy | Precision | Recall | Specificity | F2-Score | Jaccard | Dice |
|---|---|---|---|---|---|---|---|
| U-Net-VGG-16 | 93.00 ± 10.91 | 80.31 ± 31.35 | 65.07 ± 37.70 | 99.00 ± 2.25 | 65.45 ± 36.70 | 59.66 ± 35.32 | 67.04 ± 35.39 |
| U-Net-Densenet121 | 94.43 ± 9.78 | 89.83 ± 21.63 | 77.39 ± 33.28 | 99.06 ± 2.18 | 76.41 ± 31.97 | 69.35 ± 31.55 | 76.33 ± 30.39 |
| LinkNet-VGG-16 | 93.50 ± 10.60 | 83.31 ± 28.49 | 69.52 ± 36.50 | 99.28 ± 1.76 | 69.51 ± 35.31 | 63.24 ± 33.86 | 70.61 ± 33.68 |
| LinkNet-Densenet121 | 94.59 ± 9.61 | 88.65 ± 18.25 | 80.23 ± 30.78 | 99.05 ± 1.92 | 79.18 ± 29.26 | 71.84 ± 29.25 | 79.07 ± 27.07 |
| Vázquez et al. [39] | 96.77 | - | - | - | - | 56.07 | - |
| Wichakam et al. [37] | - | 88.84 | 78.14 | - | - | 69.36 | 78.61 |
| Wickstrøm et al. [41] | 94.90 | - | - | - | - | 58.70 | - |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sánchez-Peralta, L.F.; Picón, A.; Antequera-Barroso, J.A.; Ortega-Morán, J.F.; Sánchez-Margallo, F.M.; Pagador, J.B. Eigenloss: Combined PCA-Based Loss Function for Polyp Segmentation. Mathematics 2020, 8, 1316. https://doi.org/10.3390/math8081316
Sánchez-Peralta LF, Picón A, Antequera-Barroso JA, Ortega-Morán JF, Sánchez-Margallo FM, Pagador JB. Eigenloss: Combined PCA-Based Loss Function for Polyp Segmentation. Mathematics. 2020; 8(8):1316. https://doi.org/10.3390/math8081316
Chicago/Turabian StyleSánchez-Peralta, Luisa F., Artzai Picón, Juan Antonio Antequera-Barroso, Juan Francisco Ortega-Morán, Francisco M. Sánchez-Margallo, and J. Blas Pagador. 2020. "Eigenloss: Combined PCA-Based Loss Function for Polyp Segmentation" Mathematics 8, no. 8: 1316. https://doi.org/10.3390/math8081316