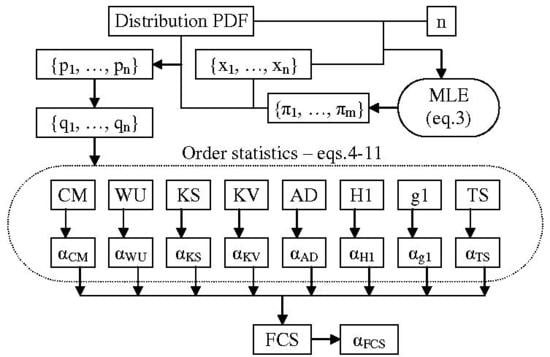
2.1. Addressing the Computation of for (s)
A method of constructing the observed distribution of the
statistic, Equation (
11), has already been reported elsewhere [
15]. A method of constructing the observed distribution of the Anderson–Darling (
) statistic, Equation (
9), has already been reported elsewhere [
17]; the method for constructing the observed distribution of any
via Monte Carlo (
) simulation, Equations (
5)–(
12), is described here and it is used for
, Equation (
12).
Let us take a sample size of
n. The MC simulation needs to generate a large number of samples (let the number of samples be
m) drawn from uniform continuous distribution (
in Equation (
2)). To ensure a good quality MC simulation, simply using a random number generator is not good enough. The next step (Equations (
10)–(
12) do not require this) is to sort the probabilities to arrive at
from Equation (
4) and to calculate an
(an order statistic) associated with each sample. Finally, this series of sample statistics (
in
Figure 1) must be sorted in order to arrive at the population emulated distribution. Then, a series of evenly spaced points (from 0 to 1000 in
Figure 1) corresponding to fixed probabilities (from
to
in
Figure 1) is to be used saving the (
statistic, its observed
probability) pairs (
Figure 1).
The main idea is how to generate a good pool of random samples from a uniform
distribution. Imagine a (pseudo) random number generator,
, is available, which generates numbers from a uniform
distribution, from a
interval; such an engine is available in many types of software and in most cases, it is based on Mersenne Twister [
18]. What if we have to extract a sample of size
? If we split in two the
interval (then into
and
) then for two values (let us say
and
), the contingency of the cases is illustrated in
Figure 2.
According to the design given in
Figure 2, for 4 (=22) drawings of two numbers (
and
) from the [0, 1) interval, a better uniform extraction (
, ‘distinguishable’) is (“00”) to extract first (
) from [0, 0.5) and second (
) from [0, 0.5), then (“01”) to extract first (
) from [0, 0.5) and second (
) from [0.5, 1), then (“10”) to extract first (
) from [0, 0.5) and second (
) from [0.5, 1), and finally (“11”) to extract first (
) from [0.5, 1) and second (
) from [0.5, 1).
An even better alternative is to do only 3 (=2 + 1) drawings (
, ‘undistinguishable’), which is (“0”) to extract both from [0, 0.5), then “1”) to extract one (let us say first) from [0, 0.5), and another (let us say second) from [0.5, 1), and finally, (“2”) to extract both from [0.5, 1) and to keep a record for their occurrences (1, 2, 1), as well. For
n numbers (
Figure 3), it can be from [0, 0.5) from 0 to
n of them, with their occurrences being accounted for.
According to the formula given in
Figure 3, for
n numbers to be drawn from [0, 1), a multiple of
drawings must be made in order to maintain the uniformity of distribution (
w from
Figure 1 becomes
). In each of those drawings, we actually only pick one of
n (random) numbers (from the [0, 1) interval) as independent. In the
-th drawing, the first
j of them are to be from [0, 0.5), while the rest are to be from [0.5, 1). The algorithm implementing this strategy is given as Algorithm 1.
Algorithm 1 is ready to be used to calculate any
(including the
first reported here). For each sample drawn from the
distribution (the array
v in Algorithm 1), the output of it (the array
u and its associated frequencies
can be modified to produce less information and operations (Algorithm 2). Calculation of the
(
output value in Algorithm 2) can be made to any precision, but for storing the result, a
data type (4 bytes) is enough (providing seven significant digits as the precision of the observed
of the
). Along with a
data type (
j output value in Algorithm 2) to store each sampled
, 5 bytes of memory is required, and the calculation of
can be made at a later time, or can be tabulated in a separate array, ready to be used at a later time.
| Algorithm 1: Balancing the drawings from uniform distribution. |
| Input data: n (2 ≤ n, integer) |
| Steps: |
| For i from 1 to n do v[i] ← Rand |
| For j from 0 to n do |
| For i from 1 to j do u[i] ← v[i]/2 |
| For i from j+1 to n do u[i] ← v[i]/2+1/2 |
| occ ← n!/j!/(n-j)! |
| Output u[1],..., u[n], occ |
| EndFor |
| Output data: (n+1) samples (u) of sample size (n) and their occurrences (occ) |
| Algorithm 2: Sampling an order statistic (). |
| Input data: n (2 ≤ n, integer) |
| Steps: |
| For i from 1 to n do v[i] ← Rand |
| For j from 0 to n do |
| For i from 1 to j do u[i] ← v[i]/2 |
| For i from j+1 to n do u[i] ← v[i]/2+1/2 |
| OSj ← any Equations (5)–(12) with p u[1],..., p u[n] |
| Output OSj, j |
| EndFor |
| Output data: (n+1) OS and their occurrences |
As given in Algorithm 2, each use of the algorithm sampling
will produce two associated arrays:
(
data type) and
j (
data type); each of them with
values. Running the algorithm
times will require
bytes for storage of the results and will produce
s, ready to be sorted (see
Figure 1). With a large amount of internal memory (such as 64 GB when running on a 16/24 cores 64 bit computers), a single process can dynamically address very large arrays and thus can provide a good quality, sampled
. To do this, some implementation tricks are needed (see
Table 1).
Depending on the value of the sample size (
n), the number of repetitions (
) for sampling of
, using Algorithm 2, from
runs, is
, while the length (
) of the variable (
) storing the dynamic array (
) from
Table 1 is
. After sorting the
s (of
, see
Table 1; total number of
) another trick is to extract a sample series at evenly spaced probabilities from it (from
to
in
Figure 1). For each pair in the sample (
varying from 0 to
= 1000 in
Table 1), a value of the
is extracted from
array (which contains ordered
values and frequencies indexed from 0 to
1), while the MC-simulated population size is
. A program implementing this strategy is available upon request (
).
The associated objective (with any statistic) is to obtain its
and thus, by evaluating the
for the statistical value obtained from the sample, Equations (
5)–(
12), to associate a likelihood for the sampling. Please note that only in the lucky cases is it possible to do this; in the general case, only critical values (values corresponding to certain risks of being in error) or approximation formulas are available (see for instance [
1,
2,
3,
5,
7,
8,
9]). When a closed form or an approximation formula is assessed against the observed values from an MC simulation (such as the one given in
Table 1), a measure of the departure such as the standard error (
) indicates the degree of agreement between the two. If a series of evenly spaced points (
points indexed from 0 to
in
Table 1) is used, then a standard error of the agreement for inner points of it (from 1 to
, see Equation (
13)) is safe to be computed (where
stands for the observed probability while
for the estimated one).
In the case of
, evenly spaced points in the interval
in the context of MC simulation (as the one given in
Table 1) providing the values of OS statistic in those points (see
Figure 1), the observed cumulative probability should (and is) taken as
, while
is to be (and were) taken from any closed form or approximation formula for the
statistic (labeled
) as
, where
are the values collected by the strategy given in
Figure 1 operating on the values provided by Algorithm 2. Before giving a closed form for
of
(Equation (
12)) and proposing approximation formulas, other theoretical considerations are needed.
2.2. Further Theoretical Considerations Required for the Study
When the
is known, it does not necessarily imply that its statistical parameters (
in Equations (
1)–(
3)) are known, and here, a complex problem of estimating the parameters of the population distribution from the sample (it then uses the same information as the one used to assess the quality of sampling) or from something else (and then it does not use the same information as the one used to assess the quality of sampling) can be (re)opened, but this matter is outside the scope of this paper.
The estimation of distribution parameters
for the data is, generally, biased by the presence of extreme values in the data, and thus, identifying the outliers along with the estimation of parameters for the distribution is a difficult task operating on two statistical hypotheses. Under this state of facts, the use of a hybrid statistic, such as the proposed one in Equation (
12), seems justified. However, since the practical use of the proposed statistics almost always requires estimation of the population parameters (and in the examples given below, as well), a certain perspective on estimation methods is required.
Assuming that the parameters are obtained using the maximum likelihood estimation method (MLE, Equation (
14); see [
19]), one could say that the uncertainty accompanying this estimation is propagated to the process of detecting the outliers. With a series of
statistics (
for Equations (
5)–(
10) and
for Equations (
5)–(
12)) assessing independently the risk of being in error (let be
those risks), assuming that the sample was drawn from the population, the unlikeliness of the event (
in Equation (
15) below) can be ascertained safely by using a modified form of Fisher’s “combining probability from independent tests” method (
, see [
10,
20,
21]; Equation (
15)), where
is the
of
distribution with
degrees of freedom.
Two known symmetrical distributions were used (
, see Equation (
1)) to express the relative deviation from the observed distribution: Gauss (
in Equation (
16)) and generalized Gauss–Laplace (
in Equation (
17)), where (in both Equations (
16) and (
17))
.
The distributions given in Equations (
16) and (
17) will be later used to approximate the
of
as well as in the case studies of using the order statistics. For a sum (
in Equation (
18)) of uniformly distributed (
) deviates (as
in Equation (
2)) the literature reports the Irwin–Hall distribution [
22,
23]. The
is: