1. Introduction
As studied in [
1], there are solid arguments to expect a vertiginous progress of nanomedicine, which is seen as the conjunction of medicine and nanotechnology. With the fabrication of nanoparticles (objects whose sizes range between 10 nm and 1000 nm), novel techniques to attack diseases have emerged [
2]. For example, in [
3], this was intensely studied based on the approach that nanoparticles can be guided through magneto-electric nanocarriers.
For example, the technique known as Targeted Drug Delivery (TDD) emerged as an accurate action against the progress of tumors in diseases related to cancer. Nevertheless, one can perceive that there is still a wide debate in literature as to the pros and cons about the injection of metal-based nanoparticles into the bloodstream [
4]. Thus, while nanoparticles transit over the bloodstream, their longevity is required in order to accomplish the objectives of therapy. Nevertheless, the sustainability of nanoparticles is affected by incorrect binding, which would decrease the effectiveness of anticancer strategies [
5]. Due to the complexity of biochemical and physical–chemical processes at the nano-level, it is logical to expect a sustainable chain of events against the central objective of the TDD scheme. For example, nanoparticles made of gold have shown undesirable side effects such as the mechanism of blood coagulation [
6]. As investigated in [
7,
8], the surface exposure of nanoparticles leads to interactions with biomolecules as well as with themselves. From this, one can see the undesired consequence in the usage of nanoparticles in the wrong reconfiguration of the biochemistry of proteins. A noteworthy example is seen in [
9], where physical effects from the injected nanoparticles might be exhibiting transformation into a type known as a “corona”.
In [
10], the electric effects of nanoparticles coated with gold aiming to unfold FibriGen (FG) by producing inflammatory events were studied; it was observed that the surface of coated nanoparticles might play a crucial role in the failure of TDD schemes.
An important point that should be stressed is the macroscopic reaction of blood against electrically charged compounds while are under interaction with cells. A notable example of this is seen when blood cells exhibit physicochemical behavior, which is known as hemagglutination [
11]. Indeed, antigen–antibody binding is strongly based on electric forces, by which the subsequent states of blood are defined. Anomalous binding would be a potential cause for the apparition of negative sequels after the injection of nanoparticles. Clearly, this would represent a disadvantage of the opted TDD scheme.
Therefore, one can wonder about the role of electrodynamics to understand the mechanism of coated nanoparticles whose surface has a direct influence on cellular uptake. For instance, in [
12], the effect of the electric charge of nanoparticles in the action of internalization was investigated. The electric effects are recognized as a sensitive point in the different schemes of drug delivery.
The sign of electric charge is seen as a noteworthy aspect, such as systems containing positively charged nanoparticles and offering interesting prospects to reach the target (tumors or cells), as studied in [
13,
14]. This would favor the mechanisms related to the uptake by molecular systems belonging to tumor tissue. Parallel effects such as the adsorption of proteins generating layers over the surface of nanoparticles would produce colloidal systems according to the so-called zeta-function [
15]. According to literature, canonical approaches based on the diffusion equation have been widely used in the study of kinetics once nanoparticles have been injected. Also, scenarios have emerged investigating the fact that internalization cannot be described by simple diffusion, as seen in [
16], where the usage of three-dimensional convection–diffusion is emphasized.
Due to the complex interactions of nanoparticles with blood, a single approach might not be suitable; thus, a single theoretical formulation describing only diffusive phenomenologies might be incomplete. Instead, an effective hybridization with other approaches is required. Therefore, the conjunction of classical electrodynamics and diffusive models emerges to be necessary in order to propose a robust model that describes the flux of nanoparticles as compounds with an electrically charged surface. It should be noted that this conjunction might not be limited to determinism; so, probabilistic events might be a fair extension of hybrid approaches [
17]. In this manner, the end-to-end process from injection to internalization can be seen as a chain of events.
This is the opted path of this paper: the construction of a hybrid model that combines diffusion with electrodynamics and might also be correlated to stochastic events in a coherent manner.
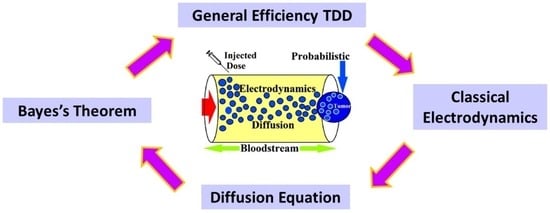
In other words, the uptake as well as internalization of electrically charged nanoparticles would be dictated by probabilistic rules. The apparition of stochastic events might be in concordance with the confluence of a plethora of variables that converts the TDD scheme in a nonlinear system from a linear to a fully nonlinear phase. An image of the central idea of the paper is displayed in
Figure 1. The rest of paper is as follows: In the second section, a macroscopic electrodynamic model of nanoparticles is presented; here, the Coulomb-like interactions are emphasized. In the third section, the diffusion approach is given. This is due to the fact that nanoparticles need to be described by a formalism that explains their diffusivity in the bloodstream. In the fourth section, some probabilistic aspects related to nanoparticles are described. In the fifth section, the Bayesian probability as the final station in the sequence of uptake and internalization emerges in a coherent manner. Finally, the conclusion of the paper is presented.
2. The Electrodynamic Model
Since nanoparticles are, in general, made of metals, citrate-coated gold nanoparticles have been demonstrated to be stable in an aqueous solution while they bear a negative charge [
18]. Furthermore, they have been shown to flip to the opposite charge over their surface. Because of this, forces with a positive sign constitute an attractor volume of albumin, which are negatively charged proteins [
19]. Imminently, the electric charge constitutes a relevant factor and the implications should be stressed within the context of TDD. Consider, for example, that nanoparticles have a spherical shape with a surface charge density given by
, by which the charge of nanoparticles can be written as
with
being the surface charge density (assumed to be constant in time for all nanoparticles). In this way, one can wonder if nanoparticles traveling along the bloodstream can lose their initial geometry [
20,
21]. In this sense, the radius might be varying in time. Thus, in this scenario, one can write the charge as
=
. For a couple of nanoparticles separated by distance
R with different radii (a particular case), the corresponding Coulomb repulsion force, with
—the dielectric constant of interstitial fluid reads
Proteins like albumin, with a negative electric charge, create aggregation over nanoparticles and electric work as well. With this, the required electric work to move a charge along displacement
can be written as:
With the energy given above, it is possible to derive the energy distribution (for all nanoparticles) based on the well-known Boltzmann–Maxwell distribution. For instance, consider a case where all nanoparticles have the same charge density
; then, the statistical distribution for all surface charge densities is written below as
where
N is a normalization constant depending on the electric characteristics of nanoparticles. To some extent, it is analogous to the case of plasma physics where the electrodynamics adjust well to kinetic theory, yielding Boltzmann–Maxwell statistics [
22]. With this, the system has a well-defined probability of surface charge density
. Indeed, it can be associated with Shannon’s entropy [
23] such that the universal probability distribution function reads
Entropy would emerge from the lapse of time by which same-sign nanoparticles are exerting forces, with each varying their transit towards the target. (Although this goes beyond the scope of paper, the electrical behavior of nanoparticles might be investigated directly with the use of theories based on thermodynamics and entropy.) In this manner, the electric work performed by nanoparticles acquires the mathematical structure of Shannon’s entropy so that W = .
On the other hand, the Coulomb force can incorporate the concept of volumetric charge density under the assumption that a transporter of nanoparticles containing a net charge exists, as commonly employed in TDD schemes [
24]. The net charge
suggests denoting the Coulomb force as
By using the sum with the restriction
= 0, one obtains
so that Equation (
5) can be written as
The focus of interest is when the cargo or transporter has a spherical geometry, where the force is written as
Some approximations are still needed; thus, the variables
s and
t are introduced. Because of this, the following changes are valid:
and
. Thus, densities are now dependent on a single variable
s having units of distance. When these densities are out of integrations, Equation (
8) acquires a simplified form:
Moreover, consider the case where nanoparticles have the same density—
=
=
; then, Equation (
9) is as follows:
Since all electrical forces along the bloodstream are of instantaneous nature, Equation (
10) is expressed as a function of a Dirac-Delta function in the sense that
In addition, the transported impulse
is given by
The impulse written above is a consequence of the usage of macroscopic observables. So, one can state that, so far, Newtonian physics support the derived expressions.
3. The Diffusion Model
It should be noted that the scenario of study in this paper has limitations. For example the opted approach is focused on a small segment of the bloodstream (for example, it can be seen in the image of
Figure 1). In the case of nanoparticles, molecular effects would emerge in a natural way; however, this effect is discarded. Because a macroscopic scenario is assumed, classical laws apply as well [
25]. It is also feasible to assume that the direction of velocity of blood flow is parallel to the longitudinal symmetry of arteries or veins. This is an important argument to neglect the effects of drag forces (as well as Brownian motion) so that the usage of the Fokker–Planck equation, for example, might not be coherent in the context of the present study. The dynamics of the injected nanoparticles into the bloodstream can be modeled, for example, by an equation of transport. Under this view, Fick’s first law applies as well. Thus, current
and nanoparticle density
are related through
=
, with
D being the diffusion constant. It should be noted that
s has units of distance. Continuity can be demanded in the sense that nanoparticles are unstoppable while they are in the bloodstream. Then, Fick’s first law is combined with the continuity equation
+
= 0. In this way, one obtains the diffusion equation
=
[
26]. It clearly demonstrates the equivalence between Fick’s first law and the diffusion equation [
27]. In the past, the diffusion equation has been used as a trusted first approximation for the transit of nanoparticles moving along the bloodstream [
28,
29,
30,
31]. Also, one can see that Equation (
12) is still incomplete because no specific information of volumetric charge densities
is known. As depicted in
Figure 1, the central idea of this paper consists in the parallel displacement of nanoparticles along the arteries. Therefore, it is suggested to employ the diffusion equation in its simplest representation (one dimension) for densities of charge that are under variation in space and time. In this way, one can use
This can be rewritten as
=
⇒
, where only the longitudinal displacement is considered, defined as
(again, it is remarked that the direction is parallel to the artery, as seen in
Figure 1). Therefore, Equation (
13) can be written as
, yielding the trivial closed-form solutions
It should be noted that
and
have units of charge per unit of volume. Solution Equation (
14) is inserted into Equation (
11), yielding that the Coulomb force now depends on the solutions of the diffusion equation. Thus, one can write
Equation (
15) denotes the Coulomb force between a pair of volumetric charge densities. However, this force depends on the diffusion equation solutions that, in turn, depend on the diffusion coefficient
D. The factor
guarantees the field-to-distance criterion.
4. Efficiency of Drug Delivery Based on Probabilities
The success of an event of drug delivery can be measured in terms of the number of nanoparticles that have been internalized into the tumor. Consider
n nanoparticles injected into the bloodstream at time
t. It is expected that at a subsequent time
, a fraction of them will reach the tumor. Here,
denotes the time at which nanoparticles reach the surface of the tumor. Thus, only a fraction of them reach the target due to interactions with blood plasma, cells, proteins, etc. [
32]. Under this view, a new quantity is defined as the efficiency of delivery, which can be written as
with
,
and
being the number of effective nanoparticles that have reached the target, the ones that are free of interactions (that are not undergoing electrical interactions) and the ones that have had chemical or electrical rejection along their path to the tumor, respectively. It should be remarked that
=
is the total number of injected nanoparticles.
Equation (
16) can be seen from another angle, whereby this efficiency abandons its deterministic status and departs to a probabilistic territory. This can be written as
Under the assumption that
for
, Equation (
17) can be written again as
If the rate
is proportional to
t, then the negative exponential might be seen as a pessimistic scenario in which the efficiency falls down in time. Equation (
18) also manifests that the entire process of drug delivery would be in risk. Therefore, biochemical compounds and proteins like albumin would decrease the chance to maximize the efficiency of sent doses. Then, it is strongly desired that such efficiency exhibits the highest values. Mathematically speaking, it is desired that efficiency behaves as a distribution that exhibits peaks [
33].
With the existence of such negative aspects, it is clear to expect the failure of the TDD scheme. A crude view of the TDD scheme might be to consider to the system composed by the nanoparticles–tumor pair through the formulation of signal and background. From this idea, efficiency can be also be written by another equation that reads
with
(background) being the ones that were rejected by the target. Thus, one can wonder as to what is the probability that a number of injected nanoparticles can reach their target while conserving their biochemical and electrical properties? Inspired by probabilistic matrix factorization (Equation (
3) of Ref. [
34], by which a form of conditional probability was anticipated), one can expect a product of probabilities. The probability of internalization can be written as a function of a finite number of probabilistic variables
(including the random ones, if any) as follows:
4.1. Gaussian Distributions
From Equation (
18), the well-known Gaussian distributions can be derived inside the context of TDD. Consider the assumption that
with
being a free parameter. From Equation (
18), one obtains the following:
by which one can recognize the case of
ℓ = 2 as the Gaussian profile. When
=
, Equation (
22) can be also written as
with
being the critical time that yields the highest probability of event. But, of course, it would not be the only probabilistic manifestation of an event involving the internalization or rejection of nanoparticles (see again Ref. [
14]).
One can define more assumptions from Equation (
18) under a time-dependent scenario. In order to explore more probability distribution functions that would emerge inside this context, consider the approximation
Some restrictions on them can be applied such as, for example, the requirement
in the scenario where the number of nanoparticles free of interaction is bigger than that of the ones that reached the target (which is a pessimistic scenario). Then, one can write down
with
units of frequency. The sinusoidal behavior of the rate
/
can be understood in terms of electrical oscillations originating from Coulomb forces.
4.2. Weibull and Lorentzian Distributions
The Gaussian distribution might not be the unique distribution that models the efficiency of nanoparticles. With Equations (21), (22) and (25) one obtains
that takes the form of the well-known Weibull distributions. Equation (
28) expresses the fact that the efficiency of injected nanoparticles acquires a maximum for some values of free parameters
and
, which would give the peaks of distributions. Turning now to Equation (
17), one can see that with the replacements from Equations (21), (24) and (25) one obtains
It is evident that a peaked behavior emerges with
ℓ = 2. Such a form is known as the Lorentzian distribution with the change
and it reads
with
being the critical time, as written in Equation (
23).
More distributions can also be generated. Consider, for example, the following definition:
As a consequence, Equation (
18) can be rewritten as
Now, one can see that
with units of
is also affected by the exponent
ℓ. Inspired by the deterministic relation
, with
F and
m being the mechanical force and mass of nanoparticles, respectively,
. In conjunction to this,
, which conveys to write down an equation for the efficiency as follows:
with
v being the velocity of nanoparticles (which is assumed to be the same of blood in the artery). The function
is not fully unknown. This can be derived from the existence of a flux of probability
, which can be written as
Because there is a degradation of the initial volume of injected nanoparticles with time, the negative derivative of flux with respect to velocity restores the efficiency and reads
Therefore,
=
. It is noteworthy that
can be well related to a Weibull distribution. For example, in the case when
ℓ = 2, one arrives at the efficiency per unit of velocity by
One can note that
acquires units of
while
has units of flux. It is clear that the TDD scheme is not based on a single group velocity along the bloodstream. Instead, the efficiency is constituted by the finite contribution of a set of velocities corresponding to several segments
.
As seen in [
35], injected drug delivery would exhibit different dynamics depending on the transit along the arteries in conjunction with the different cells that undergo interactions with nanoparticles. Thus, for example, the drug absorption is a consequence of the net efficiency among the vascular, extracellular and antigen-binding channels. By virtue of repulsion and attraction forces among nanoparticles due to Coulomb’s law (Equation (
31) of Ref. [
36]), one can assume that
. Inserting this into Equation (
22), for
J, one obtains aggregations of nanoparticles:
and for
, it means all aggregations of nanoparticles arrive at the same velocity and time (with
); then, the efficiency has the form
It is noted that the velocity v was rewritten as , with being the critical distance that plays the role as phase in the sense that there exists a minimal time that makes the arrival of nanoparticles to the target different.
In
Figure 2 above, the cases of up to three critical distances when
have been plotted.
4.3. The Diffusion–Coulomb Efficiency
The fact that equations above have suggested to some extent the incorporation of probabilistic ingredients for a robust formulation, one can go back to Equation (
16) to replace the diffusion and electrodynamics. Thus, in the first instance, one can write
In a minimal model (where nanoparticles defined as
,
and
exhibit the same diffusion and electrodynamics), the term
is common to all of them. This implies the need to simplify Equation (
40). Thus, one arrives at a compact form of efficiency:
Consider the change
by which rejected nanoparticles acquire a random distance
after failing to internalize the tumor. Here, it should be noted that there exists the possibility that nanoparticles can pass through the tumor in the hypoxia region. Clearly, this is against the purpose of TDD schemes. Only the evidence at the patient’s outcomes, so as to observe the effect of injected dose delivery and its relation to the percentage of tumor degradation, can be relevant to estimate the randomness of the scheme. Consider now an optimistic scenario by which
; then, Equation (
42) depends directly on the quantity of nanoparticles in the assumed cases and the fraction
, because Equation (
41) is rewritten as
In order to interpret Equation (
42), special attention has to be paid to the term that gives accounts of rejected ones. To accomplish this, some approximations were applied. For example,
and, with this, the numerator has the value of 2. Besides, as assumed above, the fraction
. As usual,
D has units of
. The exponential part is
with
; then, from above,
=
=
with
approximated to be 1 in units of time. With these calculations, one can rewrite Equation (
42) as
=
with
with units of
. In praxis,
is a parameter that can be known from the nanoparticles’ manufacturer and can acquire the value of 1. The why of the sinusoid approximation is because the expected flipping property produces either attraction or rejection.
In
Figure 3, the corresponding contours plot Equation (
42) are displayed. It is easy to see that in a scenario dictated by determinism, one would obtain only lines showing the linearities of the simple dynamics of nanoparticles by following the same blood velocity. However, the left-side and right-side panels show a nontrivial morphology, a fact that allows the incorporation of probabilistic aspects as a direct counterpart of determinism. As seen in the left-side panel of
Figure 3, the contour plot exhibiting the maximum value of efficiency turned out to be in the order of 12%, which is favorable in the sense that a small efficiency translates to a poor Coulomb interaction among the nanoparticles such that there is a chance that a substantial fraction of them might reach their target with minimal electrical interaction. In other words, electrical interactions would trigger noise or background effects on the TDD scheme. In the right-side panel, one can observe arrows pointing to the values of null efficiency due to Coulomb forces working against the propagation of nanoparticles (the reader should note that, so far, a hybrid description combing probability, electrodynamics and diffusion has been presented). In fact, for distances of 6.6 to 7.8 (a.u.) and for times of 2.5 (a.u.), one can see that the supposed flux of nanoparticles exhibit a slow displacement that is free of Coulomb interactions. In contrast with other space–time regions, the fact that the nanoparticles are traveling fast might not be guaranteeing optimal drug delivery; instead, it would be affected by Coulomb interactions as well as randomness.
5. Identification of Stochastic Events through Bayes’s Theorem
The use of the relation of efficiency
=
can be associated in a straightforward manner to the well-known Bayes’s theorem. Nevertheless, a kind of balance should be applied such that
≈
. Only this assumption converts the efficiency into one probabilistic relation compatible with Bayes scheme. With this, it is not difficult to corroborate that Equation (
42) has, to some extent, the structure of Bayes’s theorem [
38] known as
which, applied onto Equation (
43), acquires the following meaning if and only if
: with
T being the total number of sent nanoparticles.
, the probability that N nanoparticles arrive at the tumor;
, the probability that all of them achieve to internalize the tumor;
, the probability that M nanoparticles fail to reach the tumor;
, the probability that is wrong and nanoparticles were scattered off the tumor.
This is displayed in the image of
Figure 4. It is clear that a number of nanoparticles
N can be internalized (also into the hypoxic zone, since there is no blockade reaction of tumor cells against nanoparticles) with
M being the ones that are rejected due to minimal permeation as well as chemical imbalance due to the tumor microenvironment [
39]. By taking into account all these items, the direct correspondence with Equation (
43) turns out to be
and
opts to be random since no tool would enable measurement of the verification if
is wrong or true. This is related to the capability for enhancing the permeability of nanoparticles [
40,
41]. Indeed, the expansion
1 −
is used and, thus, Equation (
45) acquires the form
In Equation (
44), one can note that
=
. This encompasses the employed theory of the paper: Both arrival and internalization are dictated by the equation of diffusion and electrodynamics. On the other hand, the probability of confirmation is delayed to
in the sense that only evidence concerning the effects of injected drugs in patients can serve as a strong indicator of this mathematical abstraction. In this manner, from Equation (
46), the coefficients
and
can both be estimated from electrodynamics. Consider the Coulomb force for rejection (with
= 1).
, with
being the net electric charge from free ions at the bloodstream and over the target (or tumor) and
being the net charge of rejected nanoparticles. With the definition
,
, which implies that
. The same procedure is applied to estimate
, which is also expressed in terms of density as
, so that
=
=
. Now, Equation (
42) can finally be written as the conditional probability (depending on the diffusion and electrodynamics) of internalization according to
Figure 4, which reads as follows:
It is noteworthy that after applying approximations, the term that quantifies the arrival is dictated by diffusion, whereas the term of rejection is the product of variables of both diffusion and Coulomb. This product triggers the debate as to whether the shape of nanoparticles must be calibrated according to the diffusive channels that exist in human blood: minerals, plasma, albumin, etc.
Bayesian Behavior Inside Linear Scenarios
In
Figure 5, Equation (
47) or Bayes probability has been plotted for two scenarios. In both cases, one can see the deformation of the linear region as a consequence of the dynamics of nanoparticles abandoning its deterministic behavior. In this subsection, the choice
is used. In the left-side panel, the dashed line is superimposed to contour plot to note the transition between determinism and probability, where Bayes’s theorem would apply well (in the sense that the efficiency now becomes a probability). Here, the following approximation is used
≈
, as well as
→
, which also affects the exponential’s functions. The dashed line crosses the region with a high Bayes probability at around 90%. Indeed, it can be seen as a linearity between time and distance, yielding a constant velocity against the picture of classical forces (Coulomb-like for examples) governed by accelerated nanoparticles due to Newtonian forces. A different case is presented in the right-side panel where it was used
→
. The dashed line does not follow a linear behavior; instead, it demonstrates the nonlinearity of internalization in an entire Bayes scheme. For small
s, one has
≈
. These nonlinearities would be in accordance with the events where nanoparticles would arrive at the hypoxia zones [
42]. This is of importance for estimating the percent of nanoparticles that turned out to be lost and differencing them from those that were scattered off the tumor surface. In addition, one can anticipate the percent of failure against the ones that would exhibit a high probability to internalize a tumor or objective tissue [
43,
44,
45]. Thus, the difference between the percent of tumor degradation and the percent of density of injected nanoparticles would provide a test in which TDD is either purely a stochastic or deterministic process. This also would reach studies concerning angiogenesis [
46,
47]. Finally, for the processes against internalization such as retention and accumulation, although not directly observed, all of them would exhibit a side that is unfavorable to the usage of targeted drug delivery [
48], whose usage should come finally from observed outcomes of the oncological treatment of patient.