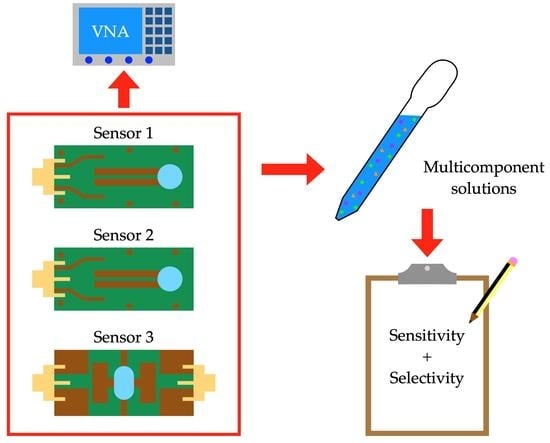
On the Selectivity of Planar Microwave Glucose Sensors with Multicomponent Solutions

Abstract

The development of glucose concentration sensors by means of microwave planar resonant technology is an active field attracting considerable attention from the scientific community. Although showing promising results, the current experimental sensors are facing some fundamental challenges. Among them, the most critical one seems to be the selectivity of glucose concentration against the variations of the concentrations of other components or parameters. In this article, we investigate the selectivity of microwave planar resonant sensors when measuring multicomponent solutions. Three sensors are involved, two of them having been designed looking for a more simplified system with a reduced size, and the third one has been specially developed to improve the sensitivity. The performance of these sensors is thoroughly assessed with a large set of measurements involving multicomponent solutions composed of pure water, NaCl, albumin at different concentrations and glucose at different concentrations. The impact of the simultaneous variations of the concentrations of glucose and albumin on the final measurements is analyzed, and the effective selectivity of the sensors is discussed. The results show a clear influence of the albumin concentration on the measurements of the glucose concentration, thereby pointing to a lack of selectivity for all sensors. This influence has been modeled, and strategies to manage this selectivity challenge are inferred.

1. Introduction

The study of sensors devoted to retrieving glucose concentration by different means has attracted the attention of a certain part of the scientific community during the last few years [1,2]. The development of glucose concentration sensors finds two main fields of application. On the one hand, they can be useful in some industrial processes aiming at the production of glucose-containing drinks, such as juices, sodas or alcohols. In these productions, glucose level becomes a key factor for the final flavor and texture of the product, as well as for complying with the applicable health regulations [3,4]. On the other hand, they find a potential application in the diabetes management context [5]. Dealing with diabetes implies the need to periodically (continuously in an ideal situation) measure the blood glucose level of the individual. Conventional methods are invasive, uncomfortable and costly, thus usually leading to a reduction of the control actions and the consequent increment of complications. Sensors able to non-invasively retrieve the patient’s glucose level in a comfortable (and ideally continuous) fashion are, therefore, highly desirable [6,7].

To that end, several technologies have been investigated for these potential applications. Within the industrial context, the existing glucose concentration measurement methods mainly rely on chemical or electrochemical probes [3]. These probes are used to involve enzymatic methods [8], although non-enzymatic ones have been developed during the last few years [4]. The non-enzymatic approach has also been proposed for the diabetes context [9,10] with interesting results in recent years [11,12]. These methods will potentially reduce the costs of current glucose concentration sensors, but they will still be limited by the need to perform the measurements in an invasive, intermittent manner.

Aiming at a continuous (and potentially non-invasive) procedure, other technologies have been studied. The predictive approach has been attempted by the development of prediction algorithms aimed at tracking the future values of the blood glucose level given the current situation, thus reducing the number of measurements [13,14,15], although not providing for the ideal solution. A variety of proposals for measuring the individual’s blood glucose level with different strategies have also been studied, such as the measurement from the breath [16,17], saliva [18,19] or tears [20,21]. With a more general glucose measurement approach, optical methods have been proposed, relying on the principles of mid- [22,23,24] and near-infrared [25,26] spectroscopy. However, the technology attracting the greatest attention for this application during the last years seems to be microwave planar devices [27,28,29,30].

Microwave planar technologies show certain advantages, such as their non-enzymatic nature, ease of integration with further equipment, low-to-moderate costs, robustness, continuous operation or possibility to function in a non-invasive way. For glucose sensing, the working principle is based on the fact that a variation in the glucose concentration yields a variation in the complex dielectric permittivity of the medium [31,32,33]. When glucose is diluted into the water at a fixed temperature, the viscosity of the solution rises with the glucose concentration [34], then increasing the dielectric relaxation time of the solution [35] and leading to changes in both the real and imaginary parts of its dielectric permittivity [36]. These variations, although having a negligible impact on the conductivity of the solution, can be effectively seen at microwave frequencies through changes in certain parameters from the sensor’s frequency-domain response [37], mainly in resonant responses [38].

In this context, several kinds of microwave resonant sensors for glucose concentration detection have been proposed. Considering the glucose concentration sensors based on the variations of the resonant frequency (f_r), to name a few, a triple complementary split-ring resonator (CSRR) [39] and a complementary electric LC resonator [40] were used with microfluidic channels, showing high sensitivities, and an SRR with the defected ground was proposed in [41] for glucose measurement in blood plasma. Regarding the sensors based on the changes in the insertion/return loss, a differential double SRR was shown in [42] for glucose measurement in microfluidic channels with high sensitivity, and a portable four SRR structure was proposed in [43] for highly-sensitive glucose level measurement, or a quarter-wavelength stub with an inter-digitated capacitor was used in [44] for accurate estimation of the glucose level in a microfluidic channel, for example. Despite the high sensibilities that can be attained [45,46], a lower number of sensors based on the variations of the phase of the scattering parameters have also been proposed [47,48].

In recent years, microwave resonant sensors based on variations of the unloaded quality factor (Q_u) have also been proposed. Recent studies have analyzed and shown their interest in the specific application of glucose concentration measurement [49]. Under this approach, a coplanar waveguide loaded with a single SRR was shown to effectively retrieve the glucose concentration in [50], a single SRR was proposed in [51] for glucose concentration in micro-liter solutions, and an asymmetric SRR was tested in [52] with good sensitivity. Due to their interest, recent studies on these sensors have tried to analyze their performance in scenarios closer to the targeted final application. Measurements on human individuals have been reported with different approaches [53,54], portable versions have been developed [55] and tested in clinical contexts with a large number of volunteers [56], or even novel biocompatible Q_u-based sensors have been proposed [49].

The results of the previous developments and the current context raise some main challenges for these sensors [57,58]. On the one hand, as with any electronic equipment, a simplification and miniaturization of the sensor and the system would be desirable, both from the integration and the reduction of error sources points of view [59,60,61]. On the other hand, as with any sensor system, higher sensitivities are desirable, especially for diabetes purposes [62,63,64]. The resolution of the final system depends on both the ability of the sensor to change its response according to the variable to be measured (sensitivity) and the ability of the instrumentation electronics to detect these changes in the sensor response. Being the latter limited by the currently available technology, increasing the sensitivity becomes essential. However, a sensitivity rise often leads to a reduction of the measurement range with acceptable linearity [65], thereby being necessary to trade-off between these two parameters according to the targeted application. Finally, restricted by the permittivity-based measurement principle, the selectivity only to glucose concentration changes has been singled out as one of the main current challenges for these sensors [28,66,67]. Very recent works have started to face the selectivity challenge by means of broadband [68] or multifrequency [69] measurements followed by a modeling and postprocessing extraction of multiple features from the sample.

As a novelty, in this work, we aim to analyze the selectivity challenge for current resonant narrowband glucose sensors. To that end, within the Q_u-based resonant sensing, we will consider a sensing approach addressing the simplification and size reduction issue [59] and a sensing approach addressing the sensitivity enhancement one [63]. We will comprehensively test the performance of these sensors with multicomponent solutions composed of pure water, salt, albumin at different concentrations and glucose at different concentrations. We will analyze the results and discuss the selectivity of these sensors to the glucose concentration against simultaneous variations of the albumin concentrations.

The paper is organized as follows: the sensors to be tested will be briefly described in Section 2, as well as the experimental procedure for the preparation of the solutions and the measurements; the results of all the measurements and the different obtained sensitivities will be shown in Section 3 and discussed in Section 4; finally, the main conclusions will be drawn in Section 5.

2. Materials and Methods

2.1. Sensors under Study

When designing microwave planar resonant sensors for glucose concentration detection, several approaches may be taken, such as for example optimizing the design in terms of the parameter from the sensor’s response that will be used to retrieve the glucose concentration [29]. In this sense, the sensor can be designed for an optimized variation of its resonant frequency (f_r), insertion/return losses, quality factor (Q_u) or phase with respect to variations in the glucose content in the solution. Some design parameters, such as the impedance of certain lines, must be tuned accordingly.

Recent works have deepened the study of Q_u-based resonant sensors and their convenience for glucose concentration tracking in aqueous solutions at frequencies under ~12 GHz [49,51]. These sensors rely on the relationship between the measured Q_u and the loss tangent of the sample (tan δ = ε″/ε′, being ε′ and ε″ the real and imaginary parts of the permittivity, respectively) for a proper configuration. In the mentioned frequency range, the dependences of ε′ and ε″ with glucose concentration have a different sign, so the relative change in tan δ is higher than that in ε′ or ε″ separately. Consequently, we will put the focus of this study on Q_u-based planar glucose sensors.

In two of our recent works, we studied the possibilities for addressing two of the current main challenges for this kind of sensor. On the one hand, in [59], we presented two sensors based on coplanar quarter-wavelength resonators with different end capacitances, with the purpose of notably reducing the sensor size and simplifying the whole system. On the other hand, in [63], we showed a strategy consisting of the mutual coupling between split-ring resonators for a considerable sensitivity improvement. In this work, we will further assess these sensors and approaches considering the third main current challenge: selectivity. To perform this, the glucose-tracking capabilities of these sensors with multicomponent solutions will be experimentally evaluated and compared.

The sensors shown in [59] are composed of coplanar quarter-wavelength one-port resonators working in reflection mode. These sensors were devised with the purpose of providing for size reduction and driving electronics simplification. Their design, shown in Figure 1, was optimized in order to avoid as much as possible the sensitivity loss due to the new constraints. They were implemented by means of a coplanar line ended in a highly capacitive disc, thus providing for an intense electric field located in a small sensing region, as it was proved desirable [62,70]. In this sense, the coplanar approach taken here is expected to compensate for the possible sensitivity loss with respect to other, more sophisticated designs. Indeed, with the aim of further studying this capacitive effect, two sensors with two different inner radii (R_in in Figure 1) for the capacitive disc were considered, thus providing for two different end capacitances in the sensing region. Henceforward, these sensors in coplanar technology will be referred to as “CS1” (R_in = 0.55 mm) and “CS2” (R_in = 0.30 mm). Some vias were implemented to achieve a better connection between the upper and lower ground planes. The coplanar structure connecting the input port with the resonator was designed to provide an adequate coupling level. The sensors were fabricated with 800 µm thick Taconic TLX-8 substrate (ε_r = 2.55, tan δ = 0.0017). The design of the sensors can be seen in Figure 1, and their dimensions are shown in

Table 1. Dimensions (in mm for lengths and in ° for angles) for the design of sensors CS1 and CS2.

Parameter	Value	Parameter	Value
α	150	f	0.40
a	3.40	g	0.80
b	3.00	h	9.70
c	1.60	Rin (CS1)	0.55
d	0.40	Rin (CS2)	0.30
e	1.60	Rout	1.20

.

The sensor presented in [63] is composed of two mutually-coupled split-ring resonators working in transmission mode. This time, the objective was to maximize the sensitivity of the Q_u of one of the resonant peaks in response to the glucose concentration in the solution by means of a more sophisticated design. This approach is based on the strong influence that the inter-resonators couplings show on the finally achieved responses in general microstrip band-pass filters [71], which has been proven effective for sensitivity enhancement [72]. In order to exploit this effect for sensing purposes, a sensor was developed by electrically coupling two identical slow-wave open-loop resonators. Direct coupling was chosen for feeding the device, implemented with two slightly asymmetrical 50 Ω I/O lines. This approach aims at boosting the unbalance due to the presence of the sample, benefiting as well from this effect [52,73]. To allow for fair comparison, the same substrate (800 µm thin Taconic TLX-8) was used. Since the device is aimed at sensing purposes, not a flat frequency response was sought, but the dimensions and coupling were tuned by simulations so that two separate resonant peaks could be seen, from which information could be obtained. The design of this two-resonator sensor (hereinafter referred to as “2RS”) can be seen in Figure 2, and its dimensions are shown in

Table 2. Dimensions (in mm) for the design of sensor 2RS.

Parameter	Value	Parameter	Value
a	2.10	f	1.70
b	2.00	g	5.10
c	0.60	h	4.00
d	2.00	i	4.60
e	1.00	j	10.70

.

To allow for measurements with liquids, three ad hoc sample holders were fabricated and glued onto the sensors (two cylindrical ones for CS1 and CS2 and a longer one for 2RS), adapting them to the sensing regions (blue dotted lines in Figure 1 and Figure 2). The sample holders were made of polytetrafluoroethylene (PTFE) due to its low-loss properties. The bottom of all the holders was made as thin as possible (~60 µm) to prevent it from masking the effect of the samples in the response of the sensor. Despite the different shapes of the sample holders, they all were designed to hold the same volume of the sample (5 µL) to allow for fair comparison. By retrofit simulations, the glue layer was estimated to be 50 µm thin with ε_r = 3.55 and tan δ = 0.01 [51]. It should be noted that this is one of the lowest sample volumes found in the literature for microwave sensors [27,28,29].

The dimensions of all the sensors were tuned so that similar operating frequencies were attained within the range of 4–4.5 GHz when pure water is considered as sample, as shown convenient for glucose measurements [67,74], thus allowing for a fair comparison. CS1 was designed to show an under-coupled resonant response, whilst CS2 was designed to show an almost critically coupled resonant response. With the aim of performing measurements with the Vector Network Analyzer (VNA), SubMiniature version A (SMA) connectors were soldered into each I/O port of the sensors. Figure 3 shows a picture of the finally implemented sensors.

The response of each sensor for the pure water measurement, already including the glued sample holder, was measured with the VNA. In terms of scattering parameters, reflection parameter (S₁₁) was measured for CS1 and CS2, and the transmission parameter (S₂₁) was measured for 2RS. These responses are plotted in Figure 4. As can be seen, a single reflection resonant peak is clearly seen for CS1 and CS2, whereas two transmission peaks are seen for 2RS, resulting from the two mutually-coupled resonators. Due to the mutual coupling, the overlapping peaks of the twin resonators split; this phenomenon is dependent on the separation between the resonators and the effective permittivity in the coupling region. Therefore, information about the sample permittivity (hence its composition) can be retrieved from the response of the device.

2.2. Experimental Procedure

2.2.1. Biological Solutions

Several sets of multicomponent biological solutions have been prepared to assess the selectivity of the variations of the glucose concentration against the variations of other components in the solution for the sensors under study. The solutions have been made with pure distilled water, salt (NaCl), albumin and glucose. It should be noted that albumin is the main protein in human blood plasma, and the study of its influence in the measurements is therefore desirable. Pure water was chosen as a simplified medium for a biological solution, considering that water makes up approximately 80% of blood. This choice also allows us to perform a comparison with other studies involving aqueous solutions, and it also eases the identification of the contribution to the measurements due to the presence of salt, albumin and glucose. To further approach the biological context, NaCl was added to all the solutions at the fixed concentration of 0.6 g/dL, which corresponds to the average physiological concentration in blood [75]. It should be noted that the detection of NaCl concentration is not pursued in this study.

Five different sets of solutions were prepared with different concentrations of bovine serum albumin (Sigma-Aldrich^® ref. A2153, from Merck KGaA, Darmstadt, Germany) and D(+)-glucose anhydrous (PanReac AppliChem ref. 131341, Castellar del Vallès, Spain). This glucose anhydrous turns to dissolved glucose when added into the solution, which will be hereafter referred to as ‘glucose’. Within each set, a fixed albumin concentration was kept for all the solutions. The albumin concentrations used in the different sets were 0.0, 2.0, 3.0, 4.0 and 5.0 g/dL, being the corresponding sets referred to as A0, A2, A3, A4 and A5, respectively. This way, the albumin concentrations found in the different sets are similar to the average physiological concentrations in blood in healthy individuals [75].

Additionally, for each set, five solutions were prepared at different glucose concentrations, keeping the NaCl and albumin concentrations fixed for the whole set. The glucose concentrations used in all the sets were 0.0, 1.5, 3.0, 4.5 and 6.0 g/dL. It should be noted that, in these conditions, the solutions show similar relative concentration ranges both for glucose and albumin, thus allowing for a fairer study of the selectivity of the sensors. These concentrations are also coherent with some industry applications, such as glucose content control in juices production, in which glucose concentrations between approximately 1.8 and 4.6 g/dL need to be monitored [76].

For preparing each set, a mother solution of 50 mL at the required albumin concentration and the fixed NaCl concentration was made. Then, from the mother solution, 5 new solutions of 10 mL each were prepared at the different glucose concentrations. The required quantities for all the solutes were accurately weighted by means of a 0.1 mg resolution Sartorius BP61S analytical balance (Sigma-Aldrich^® ref. Z408808, from Merck KGaA, Darmstadt, Germany). All the concentrations in this study are expressed in reference to the water content of the solution.

There were 25 solutions in total in this study (five sets of five solutions). These sets of solutions allow studying the influence of the variations of the glucose concentration in the measurements (within one set), as well as the influence of the variations of the albumin concentration (selecting the right solutions with a fixed glucose concentration from all the sets) and the cross-influence of the variations of both components (selecting the appropriate solutions from the sets, or selecting them all), thereby addressing the selectivity issue. The different sets of solutions are summarized in

Table 3. Sets of solutions involved in this study (concentrations in g/dL).

Set of Solutions	Fixed NaCl Concentration	Fixed Albumin Concentration	Different Glucose Concentrations
A0	0.6	0.0	0.0, 1.5, 3.0, 4.5, 6.0
A2	0.6	2.0	0.0, 1.5, 3.0, 4.5, 6.0
A3	0.6	3.0	0.0, 1.5, 3.0, 4.5, 6.0
A4	0.6	4.0	0.0, 1.5, 3.0, 4.5, 6.0
A5	0.6	5.0	0.0, 1.5, 3.0, 4.5, 6.0

.

Considering the dielectric properties of these solutions, the dielectric loss (i.e., the imaginary part of the effective permittivity, ε″) of water–glucose and water–albumin solutions shows, in general, a similar behavior for both solutes separately [68]. It would be, therefore, logical to expect a sensitivity reduction for the combined variation of both solutes in the solution, although this could also depend on other effects derived from possible interactions between these solutes. However, the relative variations of the dielectric losses for water–albumin solutions seem lower than those for water–glucose solutions, which allows us to expect reduced errors for the glucose concentration detection due to the presence of unknown concentrations of albumin, especially for comparatively low concentrations of albumin when frequencies up to ~4–5 GHz are involved. This phenomenon is expected to be more accentuated for higher frequencies (~5–15 GHz) [68].

The dielectric relaxation of water–albumin solutions at frequencies higher than ~1 GHz is largely dominated by the orientational polarization of water [77,78]. The effect of the presence of albumin in the solution produces, similarly to the effect of glucose, an increment of the viscosity, which leads to a modification of the relaxation time and, consequently, of the complex permittivity.

More specifically, the complex, frequency-dependent dielectric permittivity of the solution, ε^*(ω), can be modeled by means of the well-known Cole–Cole model [79]:

$${\epsilon }^{*}\left(\omega \right)={\epsilon }^{\prime }-j{\epsilon }^{″}={\epsilon }_{\infty }+\frac{{\epsilon }_s-{\epsilon }_{\infty }}{1+{\left(j\omega \tau \right)}^{1-\alpha }}+\frac{{\sigma }_s}{j\omega {\epsilon }_0},$$

(1)

where ω is the angular frequency, ε′ and ε″ are the real and imaginary parts of the complex permittivity, respectively, ε_∞ and ε_s are the permittivity values at low and high frequencies, τ is the relaxation time, α is a dimensionless fitting parameter, σ_s is the static ionic conductivity, and ε₀ is the permittivity of free space (8.854 × 10⁻¹² F/m). The values of the Cole–Cole parameters for a water–glucose solution and a water–albumin solution, both at 5 g/dL, separately characterized by other authors in the 20–25 °C range, are gathered in

Table 4. Cole–Cole parameters for water–glucose and water–albumin solutions at 5 g/dL concentration extracted from the literature.

Parameter	Water–Glucose Solution [33]	Water–Albumin Solution [78] 1
ε∞	4.3	6.0
εs	79.7	74.6
τ (ps)	11.1	8.3
α	neglected	0.07

¹ Values obtained from the plots in [78] with a plot digitizing software.

. It should be noted that σ_s was excluded in those parametrizations since it is considered neglectable due to the non-ionic nature of glucose and albumin. The contribution to σ_s in the solutions in this study will be uniquely provided by the ionic properties of NaCl [69].

It is important to highlight that the dielectric behavior for albumin solutions is more complex and dispersive than that for glucose solutions, composed of several relaxation times [78]. In Table 4, only the parametrization for the main relaxation process at microwave frequencies (ranging approximately 1–15 GHz) is considered, and the data for albumin solutions should consequently be taken as approximate. Table 4 shows relaxation times of similar magnitudes for glucose and albumin solutions, thus pointing to a possibility of similar relaxation processes contributing at the measuring frequencies, which could potentially interfere with and hinder the measurement. The smaller contribution of albumin to ε_s allows us to envision an influence of albumin in the measurements, but with a reduced or limited error when not very high frequencies are involved (as long as the concentrations of both solutes keep comparable), as is our case. The high similarity in ε_∞ for both cases points to a higher cross-interference and error for higher frequencies, as also discussed earlier.

2.2.2. Measurements and Data Analysis

The 25 solutions were measured with each one of the three sensors under study (CS1, CS2 and 2RS), yielding a total amount of 75 measurements. All the measurements were made with a properly calibrated VNA (Aritsu ref. MS46122A, Atsugi-shi, Japan). For each measurement, a volume of 5 µL of the corresponding solution was placed into the sample holder of the sensor by means of a precise micropipette, and the scattering parameters of the response of the sensor were recorded. The sample holder was carefully cleaned between measurements until the empty (no-sample) response was reached. The room temperature was kept constant throughout the whole measurement campaign, between 22 and 23 °C.

After performing all the measurements, they were analyzed and the data were extracted. The Q_u-based sensing approach was taken, as mentioned above, due to its interest in glucose sensing [49]. In the case of sensors CS1 and CS2, acting in reflection mode, the Q_u was obtained from the resonant peak in the S₁₁ response considering the resonant frequency, the bandwidth at −3 dB fall, and the minimum of the reflection coefficient [59]. In the specific case of CS1, due to its under-coupled nature, some responses did not show enough decrease of the S₁₁ to compute the bandwidth at −3 dB fall. Therefore, all the responses for this sensor were analyzed considering the bandwidth at −2 dB fall, although conversion to the common definition of the Q_u was later applied, as shown in [80], to provide for fair comparisons.

Considering 2RS, acting in transmission mode, the Q_u was obtained from the first peak (lower frequency peak) in the S₂₁ response, as shown in [63]. To avoid the possible influence of the second peak, bandwidths at −2 dB fall were also considered for this sensor, again providing for conversion to the common definition of the Q_u with the procedure described in [81]. In order to further analyze the capabilities of this sensor, considering both frequency peaks at the same time, the coupling factor k (as defined in [82]) was also obtained for each measurement and analyzed. The results of all the measurements will be shown in the next section.

3. Results

The results of all the measurements with the three sensors are shown in Figure 5, Figure 6, Figure 7 and Figure 8. For normalization, considering the middle point of the albumin and glucose concentrations, the operating value of Q_u for each sensor is taken as the obtained Q_u when the solution A3 with 3.0 g/dL glucose concentration (and 0.6 g/dL NaCl concentration) is measured. Figure 5, Figure 6 and Figure 7 plot the Q_u shifts relative to the operating Q_u obtained for all the measurements with CS1, CS2 and 2RS, respectively. Additionally, Figure 8 directly plots the obtained values of k for all the measurements with 2RS.

The operating parameters for each sensor are shown in

Table 5. Operating parameters for each sensor when performing the measurement of the solution A0 with 0.0 g/dL glucose concentration.

Sensor	fr0 (GHz)	Qu0	k0
CS1	4.359	47.219	—
CS2	4.334	83.191	—
2RS	4.228	43.866	217.77 × 10−4

, considering the measurement of solution A3 with 3.0 g/dL glucose concentration (and 0.6 g/dL NaCl concentration). From these parameters, the different experimentally obtained sensitivities to the glucose concentration for each sensor with each set of solutions have been computed. Nominal sensitivities for each measurement parameter (S_Qu, S_k) have been considered, as described in [83], as well as relative sensitivities to glucose for each parameter (RS(G)_Qu, RS(G)_k) for broad comparison, as described in [29]. The resulting sensitivities for all the sensors and all the sets of solutions are shown in

Table 6. Experimentally obtained sensitivities for all the sets of solutions with the three sensors.

Set of Solutions	CS1 SQu (/g/dL)	CS1 RS(G)Qu (%/%)	CS2 SQu (/g/dL)	CS2 RS(G)Qu (%/%)	2RS SQu (/g/dL)	2RS RS(G)Qu (%/%)	2RS Sk (/g/dL)	2RS RS(G)k (%/%)
water	0.384	0.799	0.743	0.869	1.962	4.115	2.49 × 10−4	1.228
A0	0.338	0.716	0.657	0.790	1.957	4.108	2.17 × 10−4	0.996
A2	0.327	0.693	0.642	0.772	1.747	3.963	2.09 × 10−4	0.960
A3	0.319	0.676	0.630	0.757	1.351	3.011	2.16 × 10−4	0.992
A4	0.313	0.663	0.627	0.754	1.283	2.860	2.14 × 10−4	0.983
A5	0.306	0.648	0.619	0.744	1.195	2.663	2.08 × 10−4	0.955

. In this table, the experimental sensitivities of these sensors when binary pure water–glucose solutions are involved [59,63] have also been included as the first set of solutions (dubbed ‘water’), which permits to identify of the influence of the presence of NaCl and albumin in the solutions. Those measurements were also performed with sample volumes of 5 µL.

Being the estimation of the glucose concentration made through variations in the measured Q_u of these sensors, which is a parameter computed from several features of the observed resonant peak [81], the real accuracy of the measurements is linked to the measurement equipment, the VNA, in our case. Some external parameters, such as the Signal-to-Noise Ratio or the frequency and amplitude resolutions, will be key for the finally achieved accuracy in each case. However, if ideal measurement conditions are considered and linearity is seen in the measurements, the Limit of Detection (LOD) of the sensors can be computed using the well-known 3σ/m rule [84], where σ is the standard deviation for the reference solution and m is the slope for the fitted model (Figure 5, Figure 6 and Figure 7). It can be seen that in our case, the slope depends on the albumin concentration, and therefore different LOD are obtained for different sets of solutions, as it also occurred with the sensitivities. The obtained LOD for the three sensors under study for the different sets of solutions when the solution with a glucose concentration of 3.0 g/dL (middle concentration) is considered as a reference and is shown in

Table 7. Obtained LOD for the three sensors considering ideal measurement conditions.

Set of Solutions	CS1 LOD (g/dL)	CS2 LOD (g/dL)	2RS LOD (g/dL)
A0	0.6222	0.2434	0.0575
A2	0.6541	0.2435	0.0668
A3	0.6564	0.2738	0.0826
A4	0.6939	0.2531	0.0851
A5	0.7509	0.2651	0.0982

.

For comparison of the results, it was difficult to find works in the literature dealing with Q_u-based microwave glucose concentration sensors involving multicomponent solutions. For a broader comparison, works involving only binary solutions can also be considered. In this sense, the reported results in this study compare well with the results of similar works in the literature, as shown in

Table 8. Comparison of the results with similar works found in the literature.

Sensor	Type of Solutions	Sample Volume	fr0 (GHz)	Qu0	RS(G)Qu (%/%)	LOD (g/dL)	Remarks
[85]	Binary	5 µL	1.11	187.14	0.186	No data	—
[50]	Binary	200 µL	2.45	60.00	0.948	No data	—
[52]	Binary	No data	4.50	116.18	1.511	No data	—
[49]	Binary	46 µL	4.62	22.00	2.727	0.103	Biocompatible
[51]	Binary	25 µL	5.16	60.65	0.978	0.356	—
[67]	Blood plasma multicomponent	25 µL	5.17	58.16	From 0.829 to 0.346	No data	Variations of glucose, ascorbic acid and lactic acid
CS1 [59]	Binary	5 µL	4.35	47.51	0.799	0.546	—
CS2 [59]	Binary	5 µL	4.36	84.97	0.869	0.214	—
2RS [63]	Binary	5 µL	4.23	47.63	4.115	0.056	—
CS1 here	Aqueous multicomponent	5 µL	4.36	47.219	From 0.716 to 0.648	From 0.622 to 0.751	Variations of glucose and albumin
CS2 here	Aqueous multicomponent	5 µL	4.33	83.191	From 0.790 to 0.744	From 0.243 to 0.265	Variations of glucose and albumin
2RS here	Aqueous multicomponent	5 µL	4.23	43.866	From 4.108 to 2.663	From 0.058 to 0.098	Variations of glucose and albumin

.

4. Discussion

The results reported in the prior section show that, from a general point of view, there is an influence of the rest of the solutes (viz. NaCl and albumin) in the experimental sensitivities of all the sensors to the glucose concentration, as well as in the LOD. This can be inferred from the trends in the plots in Figure 5, Figure 6, Figure 7 and Figure 8, as well as clearly seen in the results shown in Table 6 and Table 7. This means that not a strong selectivity is to be expected with this kind of sensor, which is a logical conclusion considering the impact that all the components have on the effective permittivity of a medium. That said, the variations in the sensitivities and LOD due to modifications of other parameters different from glucose are not constant; they seem to depend on the sensor for the setup under consideration in this study, which opens the door to the possibility of identifying different behaviors.

Considering CS1, the results (Figure 5) show a general robust behavior within each different set of solutions, including acceptable linearities. However, it can be seen in Figure 5 that different slopes are obtained for the different sets with different albumin concentrations, thus hindering the accurate measurement of the glucose concentration if the albumin concentration is not known. Regarding CS2 (Figure 6), greater sensitivities than those from CS1 have been observed, as expected, due to the higher-end capacitance in the sensing region. Notwithstanding that, similar selectivity limitations have been detected, being again difficult to identify the concentration of glucose without knowing those of the rest of the components.

The Q_u-based approach for 2SR (Figure 7) has yielded the greatest sensitivities and lowest LOD seen in this study. This can be due to the fact that this sensor takes advantage of the benefits of mutually-coupled resonators for sensing methods relying on the variations of the complex permittivity of the samples. However, a higher sensitivity does not seem to mean a higher selectivity under this scheme since, again, different slopes and behaviors have been seen. Indeed, more erratic behaviors have been observed in this case, which might be attributed to the higher sensitivity, being consequently the response of the sensor more impacted by i) the different effects due to the different combinations of concentrations of the solutes and ii) the possible instrumental error both in the preparation of the samples and in the measurement process. This behavior is also seen in the k-based approach for 2SR (Figure 8), although with more moderated sensitivities. In this particular case, being the process based on the identification of very specific frequency points (the resonant peaks), a higher error can be expected if not a high Q-factor is obtained in both peaks.

All these sensitivities are quantified in Table 6. In this sense, it is worthwhile highlighting that in all cases, the obtained sensitivities are lower than those reported for the binary (pure water–glucose) solutions. This seems a logical result considering that more lossy solutions have been involved in this study, which is coherent with the observations in [67]. Table 6 shows a clear dependence on the albumin concentration of the sensitivity to glucose for all the sensors, thus pointing to a lack of selectivity. For general comparison, the evolution of the obtained RS(G)_Qu depending on the albumin concentration is plotted in Figure 9 for the three sensors.

The RS(G)_Qu values plotted in Figure 9 have been fitted by linear least squares regression, leading to the following expressions for the RS(G)_Qu in terms of the albumin concentration (ρ_a):

$$\mathrm{CS}1:RS{\left(G\right)}_{Q_{\mathrm{u}}}=-0.0137·{\rho }_a+0.7176, R^2=0.9957,$$

(2)

$$\mathrm{CS}2:RS{\left(G\right)}_{Q_{\mathrm{u}}}=-0.0092·{\rho }_a+0.7892, R^2=0.9795,$$

(3)

$$2\mathrm{RS}:RS{\left(G\right)}_{Q_{\mathrm{u}}}=-0.3230·{\rho }_a+4.2243, R^2=0.8707.$$

(4)

Equations (2)–(4) show a clear decrease in sensitivity as the albumin concentration increases for all the sensors. This decrease appears more or less in a linear manner, which indicates a clear dependence on the albumin concentration of the sensitivity and, therefore, of the measurements. In other words, we can see here again a lack of selectivity. The fitted models are useful for effective glucose concentration tracking with these sensors on the proviso that albumin concentration is already known. From these fitted models, it is also interesting to note that the higher the bare sensitivity (for example, the sensitivity for binary solutions), the lower the linearity found in the evolution of the sensitivity with respect to the albumin concentration (in terms of R²). This is coherent with the usual trade-off found between sensitivity and linearity [65]. It should be noticed that the R² value found for 2RS might indicate that the linear fit is not a good approximation, and a more sophisticated one (polynomial, exponential…) could be sought for better sensitivity correction with respect to the albumin concentration.

The expected reduction of the sensitivities has been verified, as introduced in Section 2.2.1. More specifically, in [68], it was shown that approximately between 3 and 6 GHz, there is a trend shift in the relative variation of the ε″ of the solution due to changes in the glucose concentration (which yield a positive increment of ε″ [32,33,49]) with respect to changes in the albumin concentration (which yield a negative increment of ε″ [86]). This acts unfavorably for the Q_u-based glucose sensing approach, no longer fully benefiting from the inverse relative trends of the evolution of the ε′ and ε″ of the solution within the frequencies involved here [68,87]. This effect, added to the meager contribution to ε′ (as reported in [88]), is expected to hinder somehow the effect of the glucose concentration variations in the effective dielectric permittivity of the solution. This can explain the reduction of the sensitivities reported here, with the corresponding associated errors, which grow higher as the albumin concentration increases.

With the purpose of further analyzing this effect, we have computed the errors (in g/dL) that would appear when measuring the glucose concentration of a 1 g/dL glucose solution from each one of the sets of solutions with each sensor. In this calculation, we have considered that each sensor would have been calibrated for the A0 set of solutions (in the absence of albumin) and that the albumin concentration in the rest of the measurements would have been unknown (and, consequently, no correction would have been applied). The resulting errors are shown in

Table 9. Glucose concentration measurement errors due to the presence of albumin in the solution.

Set of Solutions	CS1 Error (g/dL)	CS1 Error (mg/dL)	CS2 Error (g/dL)	CS2 Error (mg/dL)	2RS Error (g/dL)	2RS Error (mg/dL)
A0	0.0000	0.000	0.0000	0.000	0.0000	0.000
A2	0.0325	32.544	0.0228	22.831	0.0562	56.231
A3	0.0562	56.213	0.0411	41.096	0.3096	309.640
A4	0.0740	73.964	0.0457	45.662	0.3444	344.450
A5	0.0947	94.675	0.0578	57.839	0.3892	389.241

. For the sake of understanding, the errors converted to mg/dL (usual glucose concentration units in the diabetes context) are also provided.

From Table 9, it can be seen that the reported errors here are coherent with the results reported by other authors [68], especially for low albumin concentrations. It is particularly striking the fast evolution of the error with the increase of the albumin concentration for 2RS. This effect can be attributed to the considerably higher sensitivity of this sensor, which inherently makes it more prone to measurement errors when the ideal conditions are not met. It can also be related to the measurement principle, which depends on more complex phenomena such as the couplings between the resonators or the existence of multidirectional electromagnetic fields in the region between the open ends of each resonator in addition to the inter-resonator coupling region. The exact characterization of this effect, while interesting, falls out of the scope of this work. All in all, the errors reported here due to the albumin concentration variations are not compatible with diabetes-related applications, which highlights the need to address the selectivity challenge in this context comprehensively. Notwithstanding that, depending on the application, these errors might be acceptable for some industry scenarios.

In general, the results reported here show that these sensors are capable of tracking the glucose concentration provided that the concentrations of the rest of the solutes are known. This implies that the targeted application must permit this circumstance. For instance, these sensors could be applied for real-time and even non-invasive glucose concentration track and control in some industry applications, such as the production of juices, soft drinks or spirits [3], as well as monitoring some fermentation processes [89]. The reported sensitivities and LOD, especially for 2RS, are compatible with the usual glucose concentrations to be tracked for juices production [76], provided that the rest of the components are known.

Their application to the diabetes context, however, will face a strong limitation due to their lack of selectivity, even considering the current highly-sensitive biocompatible approaches [49]. In this case, they would require accurate calibration, and their use would rely on the fast variations of the blood glucose level in comparison with the variations of the concentrations of the rest of the blood components for people with diabetes (and no further disorders). Under these circumstances, calibration would be required on a periodic basis. To perform this, comprehensive modeling of all the relevant phenomena and their influence on the measurement process would be required, such as the work shown here. Otherwise, it would be considerably difficult to apply this kind of narrowband sensors in this context, being the use of broadband sensors and comprehensive postprocessing techniques is more appropriate, as suggested in [68].

Regardless of the application, a comprehensive study and modeling of the influence of all the relevant parameters potentially impacting the sensitivity and the measurements, such as the one shown here, is advised. For applications mandatorily requiring selectivity, more sophisticated sensors will be required, or at least combinations of different sensors, the responses of which can be further processed, and multiple features can be extracted from each measurement, as shown in [90,91] for solid samples or in [69] for ternary solutions, for example. The research on multifeature extraction techniques with microwave sensors, therefore, raises as highly interesting.

5. Conclusions

In this paper, an experimental assessment and analysis of the selectivity of the glucose concentration of three microwave sensors with multicomponent solutions have been shown. Two coplanar, quarter-wavelength, one-port, Q_u-based sensors with different end capacitances have been involved, as well as a third sensor composed of two mutually-coupled, slow-wave resonators operating in Q_u-based and k-based modes. The performance of the sensors has been experimentally examined with multicomponent solutions composed of pure water, NaCl, albumin and glucose. The variations of both the concentrations of glucose and albumin have been considered for the trials. The results have shown a clear influence of the variations of the albumin concentration in the sensitivity to glucose, thus revealing a low selectivity to the variations of the glucose concentration. This influence of the albumin concentration has been modeled. The conclusions of this work point to the need to consider the selectivity issue with this kind of sensor for real applications, and they, therefore, call for research in this regard.