Sigmoidal NMFD: Convolutional NMF with Saturating Activations for Drum Mixture Decomposition
Abstract
:1. Introduction
1.1. Drum Mixture Decomposition
1.2. Non-Negative Matrix Factor Deconvolution for Drum Mixture Decomposition
1.3. Motivation for a Sigmoidal Model for the Activations
1.4. Contributions
- We reformulate the activations in the NMFD model as the product of a per-component amplitude factor, representing the relative volume of each component, with the time-varying activations for each component.
- These time-varying activations are defined as the output of a saturating sigmoidal function, and we propose a novel regularization term that combined with these saturating activations leads to binary activations. We show that in the context of automatic drum mixture decomposition, the activations are not only binary, but also become impulse-like as a consequence of this method.
- We propose different strategies and techniques to optimize the proposed model, and we rigorously evaluate their efficacy in minimizing the overall objective function for the decomposition.
- We propose metrics to evaluate the unsupervised decomposition of drum mixtures. With these, we show that the proposed algorithm achieves more impulse-like activations compared to unconstrained NMFD and sparse NMFD, making it better suited to the properties of percussive mixtures, while yielding a good decomposition and spectrogram reconstruction quality.
1.5. Structure of This Paper
2. NMFD with Saturating Activations
2.1. Sigmoidal NMFD Model
2.2. Objective Function
2.3. Optimization Procedure
2.3.1. Optimization Procedure Overview
- Calculate again with the new estimate for G;
- Update the templates , see Section 2.3.3, Equation (12);
- Calculate again with the new estimate for W;
- Repeat these steps until convergence.
2.3.2. Additive Gradient-Descent Update for G
2.3.3. Multiplicative Update for W
2.3.4. Additive Gradient-Descent Update for a
2.3.5. Optimization Strategies to Escape Local Minima
- Optimization strategy 0: straightforward optimization.In this strategy, is applied with at each iteration, and is calculated as in Equation (6) with .
- Optimization strategy 1: staged application of .In this strategy, we periodically enable and disable by alternating between “saturation sub-stages” and “fine-tuning sub-stages”, which each last several iterations. During a saturation sub-stage, , so that the activations are pushed towards saturation. During a fine-tuning sub-stage, , so that the model has time to make peaks grow or shrink against the direction imposed by , in order to escape poor local minima.
- Optimization strategy 2: moving throughout optimization.In this strategy, we impose at each iteration, i.e., for each update. In order to avoid squashing small peaks too early and additionally provide an incentive to escape local minima, we move around the “center point” of (Equation (6)) by changing in each iteration. More specifically, for each update of G and component k, we set to a random value drawn from a uniform distribution over the interval . We hypothesize that setting to a relatively low value () helps to boost relatively small peaks, and that randomly sampling could help to escape local optima.
- Optimization strategy 3: combine strategy 2 and strategy 3.This strategy combines the two aforementioned strategies: is enabled and disabled alternatingly, and when it is applied, is moved around by sampling from a uniform distribution over for each update of G.
3. Experimental Set-Up
3.1. Baseline Models
3.2. Model Initialization
3.3. Dataset
3.4. Spectrogram Representation
3.5. Evaluation Metrics
- the spectrogram is approximated well;
- all onsets in the mixture are detected, with as few false onset detections as possible;
- different components have different activation patterns: this means they contribute to the spectrogram at different times, which might indicate a more meaningful differentiation between components; and
- the activations are impulse-like.
3.5.1. Spectrogram Reconstruction Quality
3.5.2. Overall Onset Coverage
- ,
- ,
- ,
3.5.3. Activation Curve Similarity
3.5.4. Peakedness Measure
3.6. Implementation Details
4. Results
4.1. Evaluation on the ENST dataset
4.2. Evaluation of the Optimization Strategies and Techniques
- strategy 0, i.e., straightforward optimization with and “static” ;
- strategy 1, i.e., a staged application of ;
- strategy 2, i.e., setting to a random and relatively small value for each update of G;
- strategy 3, i.e., the combination of strategy 1 and strategy 2;
- each of the above, but with during the explore-and-converge stage, in order to evaluate the effect of applying the regularization less strongly during the exploration stage (for strategies 1 and 3, remains 0 during the fine-tuning sub-stages). Note that the performance of these strategies will still be evaluated with the original formulation of , i.e., with .
- the component-wise normalization of the gradients of G and a when performing the updates;
- the unconstrained warm-up stage, i.e., performing a few iterations of unconstrained optimization before is applied; and
- the step-wise adaptation of the learning rate throughout the optimization procedure.
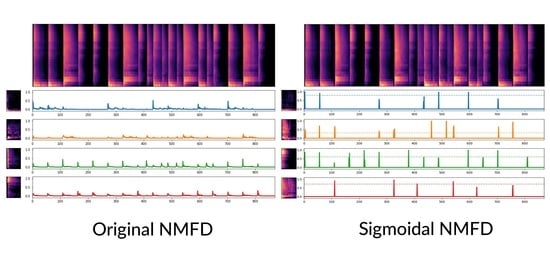
4.3. Example Decomposition
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| ADT | Automatic Drum Transcription |
| KL divergence | Kullback–Leibler divergence |
| MAE | Mean Absolute Error |
| NMF | Non-negative matrix factorization |
| NMFD | Non-negative matrix factor deconvolution |
| STFT | Short-Time Fourier Transform |
Appendix A. Derivation of the Update Rules for Sigmoidal NMFD
Appendix A.1. Additive Gradient-Descent Update for G
Appendix A.2. Multiplicative Update for W
Appendix A.3. Additive Gradient-Descent Update for a
References
- Dittmar, C.; Müller, M. Reverse Engineering the Amen Break-Score-Informed Separation and Restoration Applied to Drum Recordings. IEEE/ACM Trans. Audio Speech Lang. Process. 2016, 24, 1535–1547. [Google Scholar] [CrossRef]
- López-Serrano, P.; Davies, M.E.P.; Hockman, J.; Dittmar, C.; Müller, M. Break-Informed Audio Decomposition For Interactive Redrumming. In Proceedings of the 19th International Society for Music Information Retrieval Conference (ISMIR 2018)—Late-Breaking/Demos Session, Paris, France, 23–27 September 2018. [Google Scholar]
- Wu, C.W.; Dittmar, C.; Southall, C.; Vogl, R.; Widmer, G.; Hockman, J.; Mulleinr, M.; Lerch, A.; Müller, M. A Review of Automatic Drum Transcription. IEEE/ACM Trans. Audio Speech Lang. Process. 2018, 26, 1457–1483. [Google Scholar] [CrossRef] [Green Version]
- Vogl, R.; Dorfer, M.; Widmer, G.; Knees, P. Drum Transcription via Joint Beat and Drum Modeling using Convolutional Recurrent Neural Networks. In Proceedings of the 18th International Society for Music Information Retrieval Conference (ISMIR 2017), Suzhou, China, 23–27 October 2017; pp. 150–157. [Google Scholar]
- Southall, C.; Stables, R.; Hockman, J. Automatic Drum Transcription Using Bi-Directional Recurrent Neural Networks. In Proceedings of the 17th International Society for Music Information Retrieval Conference (ISMIR 2016), New York, NY, USA, 7–11 August 2016. [Google Scholar]
- Southall, C.; Stables, R.; Hockman, J. Automatic drum transcription for polyphonic recordings using soft attention mechanisms and convolutional neural networks. In Proceedings of the 18th International Society for Music Information Retrieval Conference (ISMIR 2017), Suzhou, China, 23–27 October 2017; pp. 606–612. [Google Scholar]
- Dittmar, C.; Gärtner, D. Real-Time Transcription and Separation of Drum Recordings Based on NMF Decomposition. In Proceedings of the 17th International Conference on Digital Audio Effects (DAFx 2014), Erlangen, Germany, 1–5 September 2014; pp. 187–194. [Google Scholar]
- Wu, C.W.; Lerch, A. From Labeled To Unlabeled Data—On the Data Challenge in Automatic Drum Transcription. In Proceedings of the 19th International Society for Music Information Retrieval Conference (ISMIR 2018), Paris, France, 23–27 September 2018. [Google Scholar]
- Smaragdis, P. Non-negative matrix factor deconvolution; extraction of multiple sound sources from monophonic inputs. In Proceedings of the 5th International Conference on Independent Component Analysis and Blind Signal Separation (ICA 2004), Granada, Spain, 22–24 September 2004; pp. 494–499. [Google Scholar]
- Roebel, A.; Pons, J.; Liuni, M.; Lagrangey, M. On Automatic Drum Transcription using Non-Negative Matrix Deconvolution and Itakura Saito Divergence. In Proceedings of the 2015 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP 2015), South Brisbane, Australia, 19–24 April 2015; pp. 414–418. [Google Scholar]
- Schmidt, M.N.; Mørup, M. Nonnegative matrix factor 2-D deconvolution for blind single channel source separation. In Proceedings of the 6th International Conference on Independent Component Analysis and Blind Signal Separation (ICA 2006), Charleston, SC, USA, 5–8 March 2006; pp. 700–707. [Google Scholar]
- Lindsay-Smith, H.; McDonald, S.; Sandler, M. Drumkit Transcription via Convolutive NMF. In Proceedings of the 15th International Conference on Digital Audio Effects (DAFx 2012), York, UK, 17–21 September 2012; pp. 15–18. [Google Scholar]
- Laroche, C.; Papadopoulos, H.; Kowalski, M.; Richard, G. Drum extraction in single channel audio signals using multi-layer Non negative Matrix Factor Deconvolution. In Proceedings of the 2017 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP 2017), New Orleans, LA, USA, 5–9 March 2017; pp. 46–50. [Google Scholar]
- Ueda, S.; Shibata, K.; Wada, Y.; Nishikimi, R.; Nakamura, E.; Yoshii, K. Bayesian Drum Transcription Based On Nonnegative Matrix Factor Decomposition with a Deep Score Prior. In Proceedings of the 2019 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP 2019), Brighton, UK, 12–17 May 2019; pp. 456–460. [Google Scholar]
- Dittmar, C.; Müller, M. Towards transient restoration in score-informed audio decomposition. In Proceedings of the 18th International Conference on Digital Audio Effects (DAFx 2015), Trondheim, Norway, 30 November–3 December 2015; pp. 1–8. [Google Scholar]
- Liutkus, A.; Badeau, R. Generalized Wiener filtering with fractional power spectrograms. In Proceedings of the 2015 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP 2015), South Brisbane, Australia, 19–24 April 2015; pp. 266–270. [Google Scholar]
- Vande Veire, L.; De Boom, C.; De Bie, T. Adapted NMFD update procedure for removing double hits in drum mixture decompositions. In Proceedings of the 13th International Workshop on Machine Learning and Music at ECML PKDD 2020 (MML2020), Ghent, Belgium, 14–18 September 2020; pp. 10–14. [Google Scholar]
- Wu, C.W.; Lerch, A. Drum Transcription Using Partially Fixed Non-Negative Matrix Factorization With Template Adaptation. In Proceedings of the 16th International Society for Music Information Retrieval Conference (ISMIR 2015), Málaga, Spain, 26–30 October 2015. [Google Scholar]
- Virtanen, T. Monaural sound source separation by nonnegative matrix factorization with temporal continuity and sparseness criteria. IEEE Trans. Audio Speech Lang. Process. 2007, 15, 1066–1074. [Google Scholar] [CrossRef] [Green Version]
- EDM Drums—Drum Samples Kit by ProducerSpot. Available online: https://www.producerspot.com/download-free-edm-drums-drum-samples-kit-by-producerspot. (accessed on 2 December 2020).
- Gillet, O.; Richard, G. ENST-Drums: An extensive audio-visual database for drum signals processing. In Proceedings of the 7th International Society for Music Information Retrieval Conference (ISMIR 2006), Victoria, BC, Canada, 8–12 October 2006. [Google Scholar]
- McFee, B.; Lostanlen, V.; Metsai, A.; McVicar, M.; Balke, S.; Thomé, C.; Raffel, C.; Zalkow, F.; Malek, A.; Dana, D.; et al. Zenodo: Librosa/librosa: 0.8.0 (Version 0.8.0). Available online: https://zenodo.org/record/3955228#.YAqsHRZS9PY (accessed on 15 January 2021). [CrossRef]
- López-Serrano, P.; Dittmar, C.; Özer, Y.; Müller, M. NMF Toolbox: Music Processing Applications of Nonnegative Matrix Factorization. In Proceedings of the 22nd International Conference on Digital Audio Effects (DAFx-19), Birmingham, UK, 2–6 September 2019. [Google Scholar]
- Code for Sigmoidal NMFD: Convolutional NMF with Saturating Activations for Drum Mixture Decomposition. Available online: https://github.com/aida-ugent/sigmoidal-nmfd (accessed on 12 January 2021).
- Lee, D.D.; Seung, H.S. Algorithms for non-negative matrix factorization. In Proceedings of the Advances in Neural Information Processing Systems 13 (NIPS 2000), Denver, CO, USA, 29 November–4 December 1999; pp. 556–562. [Google Scholar]






| Algorithm | MAE | Overall Onset Coverage | Activations Similarity | Peakedness | |||||
|---|---|---|---|---|---|---|---|---|---|
| Pr. | Rec. | F-Score | F-Score () | Min | Mean | Max | Mean | ||
| Unconstrained NMFD | 0.025 (0.003) | 0.76 (0.15) | 0.94 (0.09) | 0.83 (0.12) | 0.63 (0.17) | 0.45 (0.12) | 0.63 (0.10) | 0.79 (0.12) | 0.42 (0.02) |
| NMFD + L1 sparsity () | 0.026 (0.003) | 0.77 (0.15) | 0.94 (0.09) | 0.84 (0.12) | 0.61 (0.18) | 0.39 (0.13) | 0.59 (0.10) | 0.77 (0.12) | 0.43 (0.02) |
| NMFD + L1 sparsity () | 0.037 (0.005) | 0.76 (0.16) | 0.91 (0.09) | 0.82 (0.12) | 0.50 (0.18) | 0.04 (0.10) | 0.19 (0.10) | 0.65 (0.21) | 0.45 (0.08) |
| NMFD + L1 sparsity () | 0.071 (0.009) | 0.88 (0.15) | 0.84 (0.13) | 0.85 (0.13) | 0.35 (0.17) | 0.15 (0.31) | 0.57 (0.25) | 0.90 (0.26) | 0.46 * (0.13) |
| Sigmoidal NMFD (strategy 0, , constant ) | 0.044 (0.006) | 0.83 (0.17) | 0.78 (0.13) | 0.79 (0.13) | 0.70 (0.15) | 0.07 (0.12) | 0.23 (0.10) | 0.51 (0.14) | 0.72 (0.06) |
| Sigmoidal NMFD (strategy 2, ) | 0.035 (0.004) | 0.79 (0.19) | 0.88 (0.11) | 0.82 (0.14) | 0.73 (0.13) | 0.12 (0.11) | 0.28 (0.10) | 0.56 (0.15) | 0.67 (0.06) |
| Optimization Strategy | Loss Per Timestep | MAE | Overall Onset Coverage | Activations Similarity | Peakedness | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| Pr. | Rec. | F-Score | F-Score () | Min | Mean | Max | Mean | |||
| Strategy 0, | 0.26 (0.08) | 0.041 (0.006) | 0.82 (0.18) | 0.81 (0.13) | 0.80 (0.14) | 0.71 (0.16) | 0.07 (0.10) | 0.23 (0.10) | 0.56 (0.17) | 0.74 (0.05) |
| Strategy 0, | 0.24 (0.09) | 0.035 (0.004) | 0.78 (0.19) | 0.89 (0.10) | 0.82 (0.14) | 0.72 (0.14) | 0.12 (0.12) | 0.31 (0.11) | 0.60 (0.14) | 0.69 (0.05) |
| Strategy 1, | 0.24 (0.08) | 0.039 (0.005) | 0.83 (0.18) | 0.82 (0.13) | 0.81 (0.13) | 0.68 (0.16) | 0.08 (0.09) | 0.24 (0.09) | 0.55 (0.17) | 0.70 (0.04) |
| Strategy 1, | 0.24 (0.06) | 0.034 (0.004) | 0.79 (0.18) | 0.90 (0.09) | 0.83 (0.13) | 0.73 (0.13) | 0.14 (0.13) | 0.32 (0.11) | 0.61 (0.14) | 0.67 (0.05) |
| Strategy 2, | 0.23 (0.04) | 0.042 (0.006) | 0.85 (0.17) | 0.79 (0.15) | 0.80 (0.14) | 0.74 (0.16) | 0.06 (0.08) | 0.18 (0.09) | 0.45 (0.16) | 0.71 (0.07) |
| Strategy 2, | 0.20 (0.03) | 0.035 (0.004) | 0.79 (0.19) | 0.88 (0.11) | 0.82 (0.14) | 0.73 (0.13) | 0.12 (0.11) | 0.28 (0.10) | 0.56 (0.15) | 0.67 (0.06) |
| Strategy 3, | 0.21 (0.03) | 0.039 (0.005) | 0.84 (0.18) | 0.82 (0.13) | 0.82 (0.13) | 0.73 (0.13) | 0.08 (0.08) | 0.20 (0.09) | 0.48 (0.17) | 0.68 (0.07) |
| Strategy 3, | 0.22 (0.03) | 0.034 (0.004) | 0.80 (0.19) | 0.90 (0.09) | 0.83 (0.13) | 0.74 (0.12) | 0.14 (0.12) | 0.31 (0.11) | 0.59 (0.15) | 0.66 (0.05) |
| No normalization of the gradients of G (strategy 2, ) | 0.38 (0.21) | 0.041 (0.02) | 0.64 (0.17) | 0.92 (0.13) | 0.74 (0.15) | 0.60 (0.20) | 0.11 (0.10) | 0.27 (0.10) | 0.54 (0.17) | 0.71 (0.06) |
| No warm-up (strategy 0, ) | 5.90 (4.15) | 0.170 (0.10) | 0.66 (0.26) | 0.73 (0.28) | 0.65 (0.23) | 0.23 (0.27) | 0.71 (0.29) | 0.81 (0.23) | 0.90 (0.19) | 0.23 (0.24) |
| No warm-up (strategy 2, ) | 0.23 (0.13) | 0.035 (0.004) | 0.76 (0.18) | 0.89 (0.09) | 0.81 (0.13) | 0.73 (0.13) | 0.12 (0.12) | 0.29 (0.10) | 0.57 (0.13) | 0.69 (0.05) |
| Constant (Strategy 0, ) | 0.28 (0.06) | 0.044 (0.006) | 0.83 (0.17) | 0.78 (0.13) | 0.79 (0.13) | 0.70 (0.15) | 0.07 (0.12) | 0.23 (0.10) | 0.51 (0.14) | 0.72 (0.06) |
| Constant (Strategy 2, ) | 0.21 (0.03) | 0.036 (0.004) | 0.78 (0.18) | 0.87 (0.10) | 0.81 (0.12) | 0.73 (0.12) | 0.11 (0.12) | 0.28 (0.11) | 0.54 (0.13) | 0.69 (0.07) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vande Veire, L.; De Boom, C.; De Bie, T. Sigmoidal NMFD: Convolutional NMF with Saturating Activations for Drum Mixture Decomposition. Electronics 2021, 10, 284. https://doi.org/10.3390/electronics10030284
Vande Veire L, De Boom C, De Bie T. Sigmoidal NMFD: Convolutional NMF with Saturating Activations for Drum Mixture Decomposition. Electronics. 2021; 10(3):284. https://doi.org/10.3390/electronics10030284
Chicago/Turabian StyleVande Veire, Len, Cedric De Boom, and Tijl De Bie. 2021. "Sigmoidal NMFD: Convolutional NMF with Saturating Activations for Drum Mixture Decomposition" Electronics 10, no. 3: 284. https://doi.org/10.3390/electronics10030284