Impacts of Random Atomic Defects on Critical Buckling Stress of Graphene under Different Boundary Conditions
Abstract
:1. Introduction
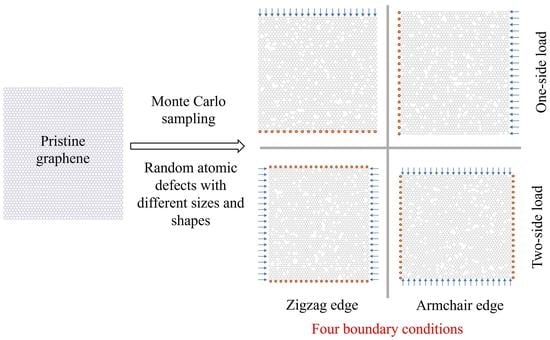
2. Graphene Geometrical Configuration
3. Boundary Conditions
4. Results and Discussion
4.1. Buckling Patterns
4.2. Statistic Results
4.3. Probability Density Distribution
5. Conclusions
- The buckling patterns and critical stress of porous graphene are sensitive to boundary conditions.
- The randomly distributed atomic vacancy defects in porous graphene destroy the regularity and symmetry of buckling patterns.
- The possibility of strengthening effects in critical buckling stress is tracked under the first, third, and fourth boundary conditions.
- The distinguishable interval ranges of probability density distribution for the relative variation of the critical buckling stress prove the promising potential of artificial control by the atomic vacancy amounts.
- It is a potentially feasible method to improve the hydrogen storage and release performance by the adaptation and change in the boundary condition of the porous graphene.
- The approximated Gaussian density distribution of critical buckling stress demonstrates the stochastic sampling efficiency by the Monte Carlo method and the artificial controllability of porous graphene.
- The results of this work provide new ideas for understanding the random porosities in buckled graphene and provide a basis for energy harvest, hydrogen storage, and artificial functionalization.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
| Mean | Maxi | Min | Variance | |
|---|---|---|---|---|
| P1 | 0.9916 | 0.9986 | 0.9835 | 0.0704 |
| P2 | 0.9804 | 1.0098 | 0.9678 | 0.1732 |
| P3 | 0.9618 | 1.0169 | 0.9444 | 0.3832 |
| P4 | 0.8886 | 0.9500 | 0.8540 | 0.3459 |
| P5 | 0.8157 | 0.8900 | 0.7714 | 0.7096 |
| Mean | Maxi | Min | Variance | |
|---|---|---|---|---|
| P1 | 0.9918 | 0.9982 | 0.9816 | 0.0175 |
| P2 | 0.9807 | 0.9913 | 0.9676 | 0.0409 |
| P3 | 0.9623 | 0.9760 | 0.9426 | 0.0824 |
| P4 | 0.8893 | 0.9139 | 0.8594 | 0.2703 |
| P5 | 0.8161 | 0.8513 | 0.7714 | 0.4892 |
| Mean | Maxi | Min | Variance | |
|---|---|---|---|---|
| P1 | 0.9976 | 1.0067 | 0.9757 | 0.2198 |
| P2 | 0.9942 | 1.0066 | 0.9680 | 0.5589 |
| P3 | 0.9878 | 1.0017 | 0.9623 | 1.1663 |
| P4 | 0.9542 | 0.9863 | 0.8694 | 5.5915 |
| P5 | 0.9071 | 0.9574 | 0.7902 | 14.0503 |
| Mean | Maxi | Min | Variance | |
|---|---|---|---|---|
| P1 | 0.9955 | 1.0046 | 0.9735 | 0.3041 |
| P2 | 0.9893 | 0.9985 | 0.9559 | 0.7886 |
| P3 | 0.9788 | 0.9965 | 0.9352 | 1.6734 |
| P4 | 0.9324 | 0.9699 | 0.8673 | 7.4369 |
| P5 | 0.8781 | 0.9600 | 0.7669 | 19.4867 |
References
- Cranford, S.W. Buckling induced delamination of graphene composites through hybrid molecular modeling. Appl. Phys. Lett. 2013, 102, 031902. [Google Scholar] [CrossRef]
- Natsuki, T.; Shi, J.X.; Ni, Q.Q. Buckling instability of circular double-layered graphene sheets. J. Phys. Condens. Matter 2012, 24, 135004. [Google Scholar] [CrossRef] [PubMed]
- Liu, X.; Wang, F.; Wu, H. Anisotropic growth of buckling-driven wrinkles in graphene monolayer. Nanotechnology 2015, 26, 065701. [Google Scholar] [CrossRef] [PubMed]
- Jiang, J.W. Buckled graphene for efficient energy harvest, storage and conversion. Nanotechnology 2016, 27, 405402. [Google Scholar] [CrossRef] [PubMed]
- Tozzini, V.; Pellegrini, V. Reversible hydrogen storage by controlled buckling of graphene layers. J. Phys. Chem. C 2011, 115, 25523–25528. [Google Scholar] [CrossRef]
- Neek-Amal, M.; Peeters, F.M. Buckled circular monolayer graphene: A graphene nano-bowl. J. Phys. Condens. Matter 2010, 23, 045002. [Google Scholar] [CrossRef]
- Zhang, C.; Song, J.; Yang, Q. Periodic buckling patterns of graphene/hexagonal boron nitride heterostructure. Nanotechnology 2014, 25, 445401. [Google Scholar] [CrossRef]
- Wang, C.G.; Lan, L.; Liu, Y.P.; Tan, H.F. Defect-guided wrinkling in graphene. Comput. Mater. Sci. 2013, 77, 250–253. [Google Scholar] [CrossRef]
- Zhang, T.; Li, X.; Gao, H. Defects controlled wrinkling and topological design in graphene. J. Mech. Phys. Solids 2014, 67, 2–13. [Google Scholar] [CrossRef]
- Mao, Y.; Wang, W.L.; Wei, D.; Kaxiras, E.; Sodroski, J.G. Graphene structures at an extreme degree of buckling. ACS Nano 2011, 5, 1395–1400. [Google Scholar] [CrossRef]
- Van der Lit, J.; Jacobse, P.H.; Vanmaekelbergh, D.; Swart, I. Bending and buckling of narrow armchair graphene nanoribbons via STM manipulation. New J. Phys. 2015, 17, 053013. [Google Scholar] [CrossRef]
- Pan, F.; Wang, G.; Liu, L.; Chen, Y.; Zhang, Z.; Shi, X. Bending induced interlayer shearing, rippling and kink buckling of multilayered graphene sheets. J. Mech. Phys. Solids 2019, 122, 340–363. [Google Scholar] [CrossRef]
- Penta, F.; Pucillo, G.P.; Monaco, M.; Gesualdo, A. Periodic beam-like structures homogenization by transfer matrix eigen-analysis: A direct approach. Mech. Res. Commun. 2017, 85, 81–88. [Google Scholar] [CrossRef]
- Penta, F.; Gesualdo, A. A Micro-Polar Model for Buckling Analysis of Vierendeel Periodic Beams. J. Appl. Mech. Trans. ASME 2022, 89, 031002. [Google Scholar]
- Yao, Y.; Wang, S.; Bai, J.; Wang, R. Buckling of dislocation in graphene. Phys. E Low-Dimens. Syst. Nanostruct. 2016, 84, 340–347. [Google Scholar] [CrossRef]
- Neek-Amal, M.; Peeters, F.M. Effect of grain boundary on the buckling of graphene nanoribbons. Appl. Phys. Lett. 2012, 100, 101905. [Google Scholar] [CrossRef]
- Georgantzinos, S.K.; Markolefas, S.; Giannopoulos, G.I.; Katsareas, D.E.; Anifantis, N.K. Designing pinhole vacancies in graphene towards functionalization: Effects on critical buckling load. Superlattices Microstruct. 2017, 103, 343–357. [Google Scholar] [CrossRef]
- Genoese, A.; Genoese, A.; Rizzi, N.L.; Salerno, G. Buckling analysis of single-layer graphene sheets using molecular mechanics. Front. Mater. 2019, 6, 26. [Google Scholar] [CrossRef]
- Fadaee, M. Buckling analysis of a defective annular graphene sheet in elastic medium. Appl. Math. Model. 2016, 40, 1863–1872. [Google Scholar] [CrossRef]
- Parashar, A.; Mertiny, P. Effect of van der Waals Forces on the Buckling Strength of Graphene. J. Comput. Theor. Nanosci. 2013, 10, 2626–2630. [Google Scholar] [CrossRef]
- Pelliciari, M.; Pasca, D.P.; Aloisio, A.; Tarantino, A.M. Size effect in single layer graphene sheets and transition from molecular mechanics to continuum theory. Int. J. Mech. Sci. 2022, 214, 106895. [Google Scholar] [CrossRef]
- Govind Rajan, A.; Silmore, K.S.; Swett, J.; Robertson, A.W.; Warner, J.H.; Blankschtein, D.; Strano, M.S. Addressing the isomer cataloguing problem for nanopores in two-dimensional materials. Nat. Mater. 2019, 18, 129–135. [Google Scholar] [CrossRef] [PubMed]
- Openov, L.A.; Podlivaev, A.I. Real-time evolution of the buckled Stone-Wales defect in graphene. Phys. E Low-Dimens. Syst. Nanostruct. 2015, 70, 165–169. [Google Scholar] [CrossRef]
- Grima, J.N.; Winczewski, S.; Mizzi, L.; Grech, M.C.; Cauchi, R.; Gatt, R.; Ttard, D.; Wojciechowski, K.W.; Rybicki, J. Tailoring graphene to achieve negative Poisson’s ratio properties. Adv. Mater. 2015, 27, 1455–1459. [Google Scholar] [CrossRef]
- Braun, M.; Arca, F.; Ariza, M.P. Computational assessment of Stone-Wales defects on the elastic modulus and vibration response of graphene sheets. Int. J. Mech. Sci. 2021, 209, 106702. [Google Scholar] [CrossRef]
- Chai, Q.; Wang, Y.Q. Traveling wave vibration of graphene platelet reinforced porous joined conical-cylindrical shells in a spinning motion. Eng. Struct. 2022, 252, 113718. [Google Scholar] [CrossRef]
- Wang, Y.Q.; Ye, C.; Zu, J.W. Nonlinear vibration of metal foam cylindrical shells reinforced with graphene platelets. Aerosp. Sci. Technol. 2019, 85, 359–370. [Google Scholar] [CrossRef]
- Ye, C.; Wang, Y.Q. Nonlinear forced vibration of functionally graded graphene platelet-reinforced metal foam cylindrical shells: Internal resonances. Nonlinear Dyn. 2021, 104, 2051–2069. [Google Scholar] [CrossRef]
- Chen, S.; Chrzan, D.C. Continuum theory of dislocations and buckling in graphene. Phys. Rev. B 2011, 84, 214103. [Google Scholar] [CrossRef]
- Chu, L.; Shi, J.; Yu, Y.; Souza De Cursi, E. The Effects of Random Porosities in Resonant Frequencies of Graphene Based on the Monte Carlo Stochastic Finite Element Model. Int. J. Mol. Sci. 2021, 22, 4814. [Google Scholar] [CrossRef]
- Chu, L.; Shi, J.; Braun, R. The equivalent Young’s modulus prediction for vacancy defected graphene under shear stress. Phys. E Low-Dimens. Syst. Nanostruct. 2019, 110, 115–122. [Google Scholar] [CrossRef]
- Chu, L.; Shi, J.; Souza de Cursi, E. Vibration analysis of vacancy defected graphene sheets by Monte Carlo based finite element method. Nanomaterials 2018, 8, 489. [Google Scholar] [CrossRef] [PubMed]
- Kumar, S.; Hembram, K.P.S.S.; Waghmare, U.V. Intrinsic buckling strength of graphene: First-principles density functional theory calculations. Phys. Rev. B 2010, 82, 115411. [Google Scholar] [CrossRef]














Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shi, J.; Chu, L.; Yu, Z.; Souza de Cursi, E. Impacts of Random Atomic Defects on Critical Buckling Stress of Graphene under Different Boundary Conditions. Nanomaterials 2023, 13, 1499. https://doi.org/10.3390/nano13091499
Shi J, Chu L, Yu Z, Souza de Cursi E. Impacts of Random Atomic Defects on Critical Buckling Stress of Graphene under Different Boundary Conditions. Nanomaterials. 2023; 13(9):1499. https://doi.org/10.3390/nano13091499
Chicago/Turabian StyleShi, Jiajia, Liu Chu, Zhengyu Yu, and Eduardo Souza de Cursi. 2023. "Impacts of Random Atomic Defects on Critical Buckling Stress of Graphene under Different Boundary Conditions" Nanomaterials 13, no. 9: 1499. https://doi.org/10.3390/nano13091499