Engineering the Aggregation of Dyes on Ligand-Shell Protected Gold Nanoparticles to Promote Plexcitons Formation
Abstract
:1. Introduction
2. Materials and Methods
2.1. Big Nanoparticles (BNPs) Synthesis
2.2. Small Nanoparticles (SNPs) Synthesis
2.3. Synthesis of The Nanosystems
2.4. Computational Methods
3. Results
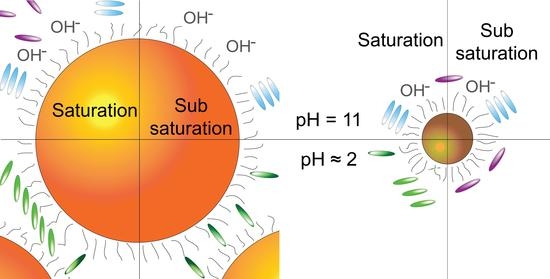
3.1. Synthesis and Photophysical Characterization of the Components of the Hybrid Nanosystems
3.2. Porphyrin Aggregation in the Presence of BNPs
3.3. Characterization of the SNPs Nanosystems
3.4. MD Simulations
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Gouterman, M. Optical Spectra and Electronic Structure of Porphyrins and Related Rings. In The Porphyrins, 1st ed.; Dolphin, D., Ed.; Academic Press: Cambridge, MA, USA, 1978; pp. 1–165. [Google Scholar]
- Kobayashi, T. (Ed.) J-Aggregates, 1st ed.; World Scientific: Singapore, 1996. [Google Scholar]
- Kobayashi, T. (Ed.) J-Aggregates, Volume 2, 1st ed.; World Scientific: Singapore, 2012. [Google Scholar]
- Collini, E.; Ferrante, C.; Bozio, R. Influence of Excitonic Interactions on the Transient Absorption and Two-Photon Absorption Spectra of Porphyrin J-Aggregates in the NIR Region. J. Phys. Chem. C 2007, 111, 18636–18645. [Google Scholar] [CrossRef]
- Bolzonello, L.; Fassioli, F.; Collini, E. Correlated Fluctuations and Intraband Dynamics of J-Aggregates Revealed by Combination of 2DES Schemes. J. Phys. Chem. Lett. 2016, 7, 4996–5001. [Google Scholar] [CrossRef] [PubMed]
- Romeo, A.; Castriciano, M.A.; Occhiuto, I.; Zagami, R.; Pasternack, R.F.; Scolaro, L.M. Kinetic Control of Chirality in Porphyrin J-Aggregates. J. Am. Chem. Soc. 2013, 136, 40–43. [Google Scholar] [CrossRef]
- Zagami, R.; Castriciano, M.A.; Romeo, A.; Trapani, M.; Pedicini, R.; Monsù Scolaro, L. Tuning Supramolecular Chirality in Nano and Mesoscopic Porphyrin J-Aggregates. Dye. Pigment. 2017, 142, 255–261. [Google Scholar] [CrossRef]
- Scolaro, L.M.; Romeo, A.; Castriciano, M.A.; Micali, N. Unusual Optical Properties of Porphyrin Fractal J-Aggregates. Chem. Commun. 2005, 24, 3018–3020. [Google Scholar] [CrossRef]
- Ribó, J.M.; Farrera, J.-A.; Valero, M.L.; Virgili, A. Self-Assembly of Cyclodextrins with Meso-Tetrakis(4-Sulfonatophenyl)Porphyrin in Aqueous Solution. Tetrahedron 1995, 51, 3705–3712. [Google Scholar] [CrossRef]
- Ribó, J.M.; Crusats, J.; Farrera, J.A.; Valero, M.L. Aggregation in Water Solutions of Tetrasodium Diprotonated Meso-Tetrakis(4-Sulfonatophenyl)Porphyrin. J. Chem. Soc. Chem. Commun. 1994, 6, 681–682. [Google Scholar] [CrossRef]
- Kano, H.; Kobayashi, T. Time-Resolved Fluorescence and Absorption Spectroscopies of Porphyrin J-Aggregates. J. Chem. Phys. 2002, 116, 184–195. [Google Scholar] [CrossRef]
- Misawa, K.; Kobayashi, T. Ultrafast Exciton and Excited-Exciton Dynamics in J-Aggregates of Three-Level Porphyrin Molecules. J. Chem. Phys. 1999, 110, 5844–5850. [Google Scholar] [CrossRef]
- Aggarwal, L.P.F.; Borissevitch, I.E. On the Dynamics of the TPPS4 Aggregation in Aqueous Solutions: Successive Formation of H and J Aggregates. Spectrochim. Acta A 2006, 63, 227–233. [Google Scholar] [CrossRef]
- Trapani, M.; De Luca, G.; Romeo, A.; Castriciano, M.A.; Scolaro, L.M. Spectroscopic Investigation on Porphyrins Nano-Assemblies onto Gold Nanorods. Spectrochim. Acta A 2017, 173, 343–349. [Google Scholar] [CrossRef] [PubMed]
- Maiti, N.C.; Ravikanth, M.; Mazumdar, S.; Periasamy, N. Fluorescence Dynamics of Noncovalently Linked Porphyrin Dimers and Aggregates. J. Chem. Phys. 1995, 99, 17192–17197. [Google Scholar] [CrossRef]
- Akins, D.L.; Zhu, H.-R.; Guo, C. Aggregation of Tetraaryl-Substituted Porphyrins in Homogeneous Solution. J. Chem. Phys. 1996, 100, 5420–5425. [Google Scholar] [CrossRef]
- Maiti, N.C.; Mazumdar, S.; Periasamy, N. J- and H-Aggregates of Porphyrin—Surfactant Complexes: Time-Resolved Fluorescence and Other Spectroscopic Studies. J. Chem. Phys. B 1998, 102, 1528–1538. [Google Scholar] [CrossRef]
- Castriciano, M.A.; Romeo, A.; Zagami, R.; Micali, N.; Scolaro, L.M. Kinetic Effects of Tartaric Acid on the Growth of Chiral J-Aggregates of Tetrakis(4-Sulfonatophenyl)Porphyrin. Chem. Commun. 2012, 48, 4872–4874. [Google Scholar] [CrossRef]
- Koti, A.S.R.; Periasamy, N. Self-Assembly of Template-Directed J-Aggregates of Porphyrin. Chem. Mater. 2003, 15, 369–371. [Google Scholar] [CrossRef]
- Koti, A.S.R.; Taneja, J.; Periasamy, N. Control of Coherence Length and Aggregate Size in the J-Aggregate of Porphyrin. Chem. Phys. Lett. 2003, 375, 171–176. [Google Scholar] [CrossRef]
- Zhang, L.; Chen, H.; Wang, J.; Li, Y.F.; Waang, J.; Sang, Y.; Xiao, S.J.; Zhan, L.; Huang, C.Z. Tetrakis(4-Sulfonatophenyl)Porphyrin-Directed Assembly of Gold Nanocrystals: Tailoring the Plasmon Coupling through Controllable Gap Distances. Small 2010, 6, 2001–2009. [Google Scholar] [CrossRef]
- Ðorđević, L.; Arcudi, F.; D’Urso, A.; Cacioppo, M.; Micali, N.; Bürgi, T.; Purrello, R.; Prato, M. Design Principles of Chiral Carbon Nanodots Help Convey Chirality from Molecular to Nanoscale Level. Nat. Commun. 2018, 9, 3442. [Google Scholar] [CrossRef]
- Magno, L.N.; Bezerra, F.C.; Freire, L.E.S.; Guerra, R.A.; Bakuzis, A.F.; Gonçalves, P.J. Use of Spectroscopic Techniques for Evaluating the Coupling of Porphyrins on Biocompatible Nanoparticles. A Potential System for Photodynamics, Theranostics, and Nanodrug Delivery Applications. J. Chem. Phys. A 2017, 121, 1924–1931. [Google Scholar] [CrossRef]
- Peruffo, N.; Gil, G.; Corni, S.; Mancin, F.; Collini, E. Selective Switching of Multiple Plexcitons in Colloidal Materials: Directing the Energy Flow at the Nanoscale. Nanoscale 2021, 13, 6005–6015. [Google Scholar] [CrossRef] [PubMed]
- Hertzog, M.; Wang, M.; Mony, J.; Börjesson, K. Strong Light-Matter Interactions: A New Direction within Chemistry. Chem. Soc. Rev. 2019, 48, 937–961. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Manuel, A.P.; Kirkey, A.; Mahdi, N.; Shankar, K. Plexcitonics-Fundamental Principles and Optoelectronic Applications. J. Mater. Chem. C 2019, 7, 1821–1853. [Google Scholar] [CrossRef]
- Baranov, D.G.; Wersäll, M.; Cuadra, J.; Antosiewicz, T.J.; Shegai, T. Novel Nanostructures and Materials for Strong Light-Matter Interactions. ACS Photonics 2018, 5, 24–42. [Google Scholar] [CrossRef]
- Hugall, J.T.; Singh, A.; Van Hulst, N.F. Plasmonic Cavity Coupling. ACS Photonics 2018, 5, 43–53. [Google Scholar] [CrossRef]
- Wiederrecht, G.P.; Hall, J.E.; Bouhelier, A. Control of Molecular Energy Redistribution Pathways via Surface Plasmon Gating. Phys. Rev. Lett. 2007, 98, 083001. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Salomon, A.; Genet, C.; Ebbesen, T.W. Molecule-Light Complex: Dynamics of Hybrid Molecule-Surface Plasmon States. Angew. Chem. Int. Ed. 2009, 48, 8748–8751. [Google Scholar]
- Fofang, N.T.; Park, T.H.; Neumann, O.; Mirin, N.A.; Nordlander, P.; Halas, N.J. Plexcitonic Nanoparticles: Plasmon–Exciton Coupling in Nanoshell–J-Aggregate Complexes. Nano Lett. 2008, 8, 3481–3487. [Google Scholar] [CrossRef]
- Yoshida, A.; Kometani, N. Effect of the Interaction between Molecular Exciton and Localized Surface Plasmon on the Spectroscopic Properties of Silver Nanoparticles Coated with Cyanine Dye J-Aggregates. J. Phys. Chem. C 2010, 114, 2867–2872. [Google Scholar] [CrossRef]
- Balci, S. Ultrastrong Plasmon–Exciton Coupling in Metal Nanoprisms with J-Aggregates. Opt. Lett. 2013, 38, 4498–4501. [Google Scholar] [CrossRef] [PubMed]
- Simon, T.; Melnikau, D.; Sánchez-Iglesias, A.; Grzelczak, M.; Liz-Marzán, L.M.; Rakovich, Y.; Feldmann, J.; Urban, A.S. Exploring the Optical Nonlinearities of Plasmon-Exciton Hybrid Resonances in Coupled Colloidal Nanostructures. J. Phys. Chem. C 2016, 120, 12226–12233. [Google Scholar] [CrossRef]
- Phuc, N.T.; Trung, P.Q.; Ishizaki, A. Controlling the Nonadiabatic Electron-Transfer Reaction Rate through Molecular-Vibration Polaritons in the Ultrastrong Coupling Regime. Sci. Rep. 2020, 10, 7318. [Google Scholar] [CrossRef] [PubMed]
- Cao, E.; Lin, W.; Sun, M.; Liang, W.; Song, Y. Exciton-Plasmon Coupling Interactions: From Principle to Applications. Nanophotonics 2018, 7, 145–167. [Google Scholar] [CrossRef]
- Takahashi, S.; Watanabe, K. Decoupling from a Thermal Bath via Molecular Polariton Formation. J. Phys. Chem. Lett. 2020, 11, 1349–1356. [Google Scholar] [CrossRef]
- Marquier, F.; Sauvan, C.; Greffet, J.J. Revisiting Quantum Optics with Surface Plasmons and Plasmonic Resonators. ACS Photonics 2017, 4, 2091–2101. [Google Scholar] [CrossRef]
- Peruffo, N.; Mancin, F.; Collini, E. Plexcitonic Nanohybrids Based on Gold Nanourchins: The Role of the Capping Layer. J. Phys. Chem. C 2021, 125, 19897–19905. [Google Scholar] [CrossRef]
- Kolaric, B.; Maes, B.; Clays, K.; Durt, T.; Caudano, Y. Strong Light–Matter Coupling as a New Tool for Molecular and Material Engineering: Quantum Approach. Adv. Quantum Technol. 2018, 1, 1800001. [Google Scholar] [CrossRef]
- Ni, W.; Yang, Z.; Chen, H.; Li, L.; Wang, J. Coupling between Molecular and Plasmonic Resonances in Freestanding Dye-Gold Nanorod Hybrid Nanostructures. J. Am. Chem. Soc. 2008, 130, 6692–6693. [Google Scholar] [CrossRef]
- Nan, F.; Zhang, Y.-F.; Li, X.; Zhang, X.-T.; Li, H.; Zhang, X.; Jiang, R.; Wang, J.; Zhang, W.; Zhou, L.; et al. Unusual and Tunable One-Photon Nonlinearity in Gold-Dye Plexcitonic Fano Systems. Nano Lett. 2015, 15, 2705–2710. [Google Scholar] [CrossRef]
- Thomas, R.; Thomas, A.; Pullanchery, S.; Joseph, L.; Somasundaran, S.M.; Swathi, R.S.; Gray, S.K.; Thomas, K.G. Plexcitons: The Role of Oscillator Strengths and Spectral Widths in Determining Strong Coupling. ACS Nano 2018, 12, 402–415. [Google Scholar] [CrossRef]
- Mohankumar, M.; Unnikrishnan, M.; Naidu, G.N.; Somasundaran, S.M.; Ajaykumar, M.P.; Swathi, R.S.; Thomas, K.G. Finding the Needle in a Haystack: Capturing Veiled Plexcitonic Coupling through Differential Spectroscopy. J. Phys. Chem. C 2020, 124, 26387–26395. [Google Scholar] [CrossRef]
- Grynberg, G.; Aspect, A.; Fabre, C. Introducion to Quantum Optics: From the Semi-Classical Approach to Quantized Light; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Gu, P.; Zhang, W.; Zhang, G. Plasmonic Nanogaps: From Fabrications to Optical Applications. Adv. Mater. Interfaces 2018, 5, 1800648. [Google Scholar] [CrossRef]
- Xia, H.; Bai, S.; Hartmann, J.; Wang, D. Synthesis of Monodisperse Quasi-Spherical Gold Nanoparticles in Water via Silver(I)-Assisted Citrate Reduction. Langmuir 2010, 26, 3585–3589. [Google Scholar] [CrossRef]
- Bonomi, R.; Cazzolaro, A.; Prins, L.J. Assessment of the Morphology of Mixed SAMs on Au Nanoparticles Using a Fluorescent Probe. Chem. Commun. 2011, 47, 445–447. [Google Scholar] [CrossRef]
- Manea, F.; Bindoli, C.; Polizzi, S.; Lay, L.; Scrimin, P. Expeditious Synthesis of Water-Soluble, Monolayer-Protected Gold Nanoparticles of Controlled Size and Monolayer Composition. Langmuir 2008, 24, 4120–4124. [Google Scholar] [CrossRef]
- van der Spoel, D.; Lindahl, E.; Hess, B.; Groenhof, G.; Mark, A.E.; Berendsen, H.J.C. GROMACS: Fast, Flexible, and Free. J. Comput. Chem. 2005, 26, 1701–1718. [Google Scholar] [CrossRef]
- Jorgensen, W.L.; Maxwell, D.S.; Tirado-Rives, J. Development and Testing of the OPLS All-Atom Force Field on Conformational Energetics and Properties of Organic Liquids. J. Am. Chem. Soc. 1996, 118, 11225–11236. [Google Scholar] [CrossRef]
- Dodda, L.S.; Cabeza de Vaca, I.; Tirado-Rives, J.; Jorgensen, W.L. LigParGen Web Server: An Automatic OPLS-AA Parameter Generator for Organic Ligands. Nucleic Acids Res. 2017, 45, W331–W336. [Google Scholar] [CrossRef] [Green Version]
- Dutta, S.; Corni, S.; Brancolini, G. Molecular Dynamics Simulations of a Catalytic Multivalent Peptide–Nanoparticle Complex. Int. J. Mol. Sci. 2022, 23, 1484. [Google Scholar] [CrossRef]
- Dutta, S.; Bellucci, L.; Agostini, M.; Gagliardi, M.; Corni, S.; Cecchini, M.; Brancolini, G. Atomistic Simulations of Gold Surface Functionalization for Nanoscale Biosensors Applications. Nanotechnology 2021, 32, 095702. [Google Scholar] [CrossRef]
- Iori, F.; Di Felice, R.; Molinari, E.; Corni, S. GolP: An Atomistic Force-Field to Describe the Interaction of Proteins With Au(111) Surfaces in Water. J. Comput. Chem. 2009, 30, 1465–1476. [Google Scholar] [CrossRef] [PubMed]
- Dubois, L.H.; Zegarski, B.R.; Nuzzo, R.G. Molecular Ordering of Organosulfur Compounds on Au(111) and Au(100): Adsorption from Solution and in Ultrahigh Vacuum. J. Chem. Phys. 1993, 98, 678–688. [Google Scholar] [CrossRef]
- Bizzarri, A.R.; Costantini, G.; Cannistraro, S. MD Simulation of a Plastocyanin Mutant Adsorbed onto a Gold Surface. Biophys. Chem. 2003, 106, 111–123. [Google Scholar] [CrossRef]
- Allen, M.P.; Tildesley, D.J. Computer Simulation of Liquids, 2nd ed.; Oxford University Press: Oxford, UK, 2017. [Google Scholar]
- Leach, A.R. Molecular Modelling: Principles and Applications, 2nd ed.; Prentice Hall: Upper Saddle River, NJ, USA, 2001. [Google Scholar]
- Van Der Spoel, D.; Van Maaren, P.J.; Berendsen, H.J.C. A Systematic Study of Water Models for Molecular Simulation: Derivation of Water Models Optimized for Use with a Reaction Field. J. Chem. Phys. 1998, 108, 10220–10230. [Google Scholar] [CrossRef] [Green Version]
- Bussi, G.; Donadio, D.; Parrinello, M. Canonical Sampling through Velocity Rescaling. J. Chem. Phys. 2007, 126, 014101. [Google Scholar] [CrossRef] [Green Version]
- Parrinello, M.; Rahman, A. Polymorphic Transitions in Single Crystals: A New Molecular Dynamics Method. J. Appl. Phys. 1998, 52, 7182–7190. [Google Scholar] [CrossRef]
- Essmann, U.; Perera, L.; Berkowitz, M.L.; Darden, T.; Lee, H.; Pedersen, L.G. A Smooth Particle Mesh Ewald Method. J. Chem. Phys. 1995, 103, 8577–8593. [Google Scholar] [CrossRef] [Green Version]
- Yeh, I.C.; Berkowitz, M.L. Ewald Summation for Systems with Slab Geometry. J. Chem. Phys. 1999, 111, 3155–3162. [Google Scholar] [CrossRef]
- Cramer, C.J. Essentials of Computational Chemistry: Theories and Models, 2nd ed.; Wiley: Chichester, UK, 2004. [Google Scholar]
- Hess, B.; Bekker, H.; Berendsen, H.J.C.; Fraaije, J.G.E.M. LINCS: A Linear Constraint Solver for Molecular Simulations. J. Comput. Chem. 1997, 18, 1463–1472. [Google Scholar] [CrossRef]
- Daura, X.; Gademann, K.; Jaun, B.; Seebach, D.; Van Gunsteren, W.F.; Mark, A.E. Peptide Folding: When Simulation Meets Experiment. Angew. Chem. Int. Ed. 1999, 38, 236–240. [Google Scholar] [CrossRef]
- Akins, D.L.; Zhu, H.-R.; Guo, C. Absorption and Raman Scattering by Aggregated Meso-Tetrakis(p-Sulfonatophenyl)Porphine. J. Phys. Chem. 1994, 98, 3612–3618. [Google Scholar] [CrossRef]
- Fleischer, E.B. Structure of Porphyrins and Metalloporphyrins. Accounts Chem. Res. 1970, 3, 105–112. [Google Scholar] [CrossRef]
- Li, J.; Ueno, K.; Uehara, H.; Guo, J.; Oshikiri, T.; Misawa, H. Dual Strong Couplings between TPPS J-Aggregates and Aluminum Plasmonic States. J. Phys. Chem. Lett. 2016, 7, 2786–2791. [Google Scholar] [CrossRef] [PubMed]
- Salomon, A.; Wang, S.; Hutchison, J.A.; Genet, C.; Ebbesen, T.W. Strong Light-Molecule Coupling on Plasmonic Arrays of Different Symmetry. ChemPhysChem 2013, 14, 1882–1886. [Google Scholar] [CrossRef]
- Chikkaraddy, R.; De Nijs, B.; Benz, F.; Barrow, S.J.; Scherman, O.A.; Rosta, E.; Demetriadou, A.; Fox, P.; Hess, O.; Baumberg, J.J. Single-Molecule Strong Coupling at Room Temperature in Plasmonic Nanocavities. Nature 2016, 535, 127–130. [Google Scholar] [CrossRef] [Green Version]
- Prasad, P.N. Nanophotonics, 1st ed.; John Wiley & Sons: Hoboken, NJ, USA, 2004; pp. 129–151. [Google Scholar]
- Waks, E.; Sridharan, D. Cavity QED Treatment of Interactions between a Metal Nanoparticle and a Dipole Emitter. Phys. Rev. A 2010, 82, 043845. [Google Scholar] [CrossRef] [Green Version]
- Siddhanta, S.; Barman, I.; Narayana, C. Revealing the Trehalose Mediated Inhibition of Protein Aggregation through Lysozyme-Silver Nanoparticle Interaction. Soft Matter 2015, 11, 7241–7249. [Google Scholar] [CrossRef]
- Li, N.; Han, Z.; Huang, Y.; Liang, K.; Wang, X.; Wu, F.; Qi, X.; Shang, Y.; Yu, L.; Ding, B.; et al. Strong Plasmon-Exciton Coupling in Bimetallic Nanorings and Nanocuboids. J. Mater. Chem. C 2020, 8, 7672–7678. [Google Scholar] [CrossRef]
- Eizner, E.; Avayu, O.; Ditcovski, R.; Ellenbogen, T. Aluminum Nanoantenna Complexes for Strong Coupling between Excitons and Localized Surface Plasmons. Nano Lett. 2015, 15, 6215–6221. [Google Scholar] [CrossRef]
- Thomas, K.G.; Kamat, P.V. Chromophore-Functionalized Gold Nanoparticles. Acc. Chem. Res. 2003, 36, 888–898. [Google Scholar] [CrossRef]
- Braun, S.; Salaneck, W.R.; Fahlman, M. Energy-Level Alignment at Organic/Metal and Organic/Organic Interfaces. Adv. Mater. 2009, 21, 1450–1472. [Google Scholar] [CrossRef]
- Tanaka, D.; Inuta, Y.; Sakamoto, M.; Furube, A.; Haruta, M.; So, Y.G.; Kimoto, K.; Hamada, I.; Teranishi, T. Strongest π-Metal Orbital Coupling in a Porphyrin/Gold Cluster System. Chem. Sci. 2014, 5, 2007–2010. [Google Scholar] [CrossRef]
- Darby, B.L.; Auguié, B.; Meyer, M.; Pantoja, A.E.; Le Ru, E.C. Modified Optical Absorption of Molecules on Metallic Nanoparticles at Sub-Monolayer Coverage. Nat. Photonics 2016, 10, 40–45. [Google Scholar] [CrossRef] [Green Version]
- Karra, S.; Wooten, M.; Griffith, W.; Gorski, W. Morphology of Gold Nanoparticles and Electrocatalysis of Glucose Oxidation. Electrochim. Acta 2016, 218, 8–14. [Google Scholar] [CrossRef] [Green Version]
- Elechiguerra, J.L.; Reyes-Gasga, J.; Yacaman, M.J. The Role of Twinning in Shape Evolution of Anisotropic Noble Metal Nanostructures. J. Mater. Chem. 2006, 16, 3906–3919. [Google Scholar] [CrossRef]
- Brancolini, G.; Kokh, D.B.; Calzolai, L.; Wade, R.C.; Corni, S. Docking of Ubiquitin to Gold Nanoparticles. ACS Nano 2012, 6, 9863–9878. [Google Scholar] [CrossRef]
- Riccardi, L.; Gabrielli, L.; Sun, X.; De Biasi, F.; Rastrelli, F.; Mancin, F.; De Vivo, M. Nanoparticle-Based Receptors Mimic Protein-Ligand Recognition. Chem 2017, 3, 92–109. [Google Scholar] [CrossRef] [Green Version]
- Riccardi, L.; Decherchi, S.; Rocchia, W.; Zanoni, G.; Cavalli, A.; Mancin, F.; De Vivo, M. Molecular Recognition by Gold Nanoparticle-Based Receptors as Defined through Surface Morphology and Pockets Fingerprint. J. Phys. Chem. Lett. 2021, 12, 5616–5622. [Google Scholar] [CrossRef]
- Piserchia, A.; Zerbetto, M.; Salvia, M.V.; Salassa, G.; Gabrielli, L.; Mancin, F.; Rastrelli, F.; Frezzato, D. Conformational Mobility in Monolayer-Protected Nanoparticles: From Torsional Free Energy Profiles to NMR Relaxation. J. Phys. Chem. C 2015, 119, 20100–20110. [Google Scholar] [CrossRef]
- Sun, X.; Riccardi, L.; De Biasi, F.; Rastrelli, F.; De Vivo, M.; Mancin, F. Molecular-Dynamics-Simulation-Directed Rational Design of Nanoreceptors with Targeted Affinity. Angew. Chem. Int. Ed. 2019, 58, 7702–7707. [Google Scholar] [CrossRef]
- Schneider, H.J.; Schiestel, T.; Zimmermann, P. The Incremental Approach to Noncovalent Interactions: Coulomb and van Der Waals Effects in Organic Ion Pairs. J. Am. Chem. Soc. 1992, 114, 7698–7703. [Google Scholar] [CrossRef]
- Pieters, G.; Cazzolaro, A.; Bonomi, R.; Prins, L.J. Self-Assembly and Selective Exchange of Oligoanions on the Surface of Monolayer Protected Au Nanoparticles in Water. Chem. Commun. 2012, 48, 1916–1918. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wu, M.; Vartanian, A.M.; Chong, G.; Pandiakumar, A.K.; Hamers, R.J.; Hernandez, R.; Murphy, C.J. Solution NMR Analysis of Ligand Environment in Quaternary Ammonium-Terminated Self-Assembled Monolayers on Gold Nanoparticles: The Effect of Surface Curvature and Ligand Structure. J. Am. Chem. Soc. 2019, 141, 4316–4327. [Google Scholar] [CrossRef] [PubMed]
- Ni, W.; Chen, H.; Su, J.; Sun, Z.; Wang, J.; Wu, H. Effects of Dyes, Gold Nanocrystals, PH, and Metal Ions on Plasmonic and Molecular Resonance Coupling. J. Am. Chem. Soc. 2010, 132, 4806–4814. [Google Scholar] [CrossRef]
- Bian, T.; Gardin, A.; Gemen, J.; Houben, L.; Perego, C.; Lee, B.; Elad, N.; Chu, Z.; Pavan, G.M.; Klajn, R. Electrostatic Co-Assembly of Nanoparticles with Oppositely Charged Small Molecules into Static and Dynamic Superstructures. Nat. Chem. 2021, 13, 940–949. [Google Scholar] [CrossRef]









| Title 1 | HCl/NaOH, μL | AuNPs (5 mM), μL | TPPS (1 mM), μL |
|---|---|---|---|
| BNPs, PAP = 0.35 | 998 | 1 | 1 |
| BNPs, PAP = 3.5 | 994 | 6 | 0.5 |
| SNPs, PAP = 0.35 | 998 | 0.5 | 1 |
| SNPs, PAP = 3.5 | 996 | 2.5 | 1 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Peruffo, N.; Parolin, G.; Collini, E.; Corni, S.; Mancin, F. Engineering the Aggregation of Dyes on Ligand-Shell Protected Gold Nanoparticles to Promote Plexcitons Formation. Nanomaterials 2022, 12, 1180. https://doi.org/10.3390/nano12071180
Peruffo N, Parolin G, Collini E, Corni S, Mancin F. Engineering the Aggregation of Dyes on Ligand-Shell Protected Gold Nanoparticles to Promote Plexcitons Formation. Nanomaterials. 2022; 12(7):1180. https://doi.org/10.3390/nano12071180
Chicago/Turabian StylePeruffo, Nicola, Giovanni Parolin, Elisabetta Collini, Stefano Corni, and Fabrizio Mancin. 2022. "Engineering the Aggregation of Dyes on Ligand-Shell Protected Gold Nanoparticles to Promote Plexcitons Formation" Nanomaterials 12, no. 7: 1180. https://doi.org/10.3390/nano12071180