Implementation of Spiegler–Kedem and Steric Hindrance Pore Models for Analyzing Nanofiltration Membrane Performance for Smart Water Production
Abstract
:1. Introduction
2. Theory
2.1. Nanofiltration Membranes
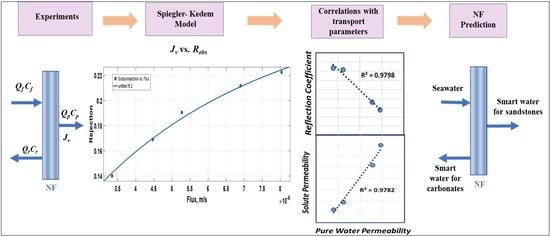
2.2. Spiegler–Kedem Model
- The hydraulic permeability Lp.
- The solute permeability Ps.
- The reflection coefficient σ.
- (1)
- The driving forces are pressure and concentration gradients.
- (2)
- The model predicts the transport of the solute and solvent through the membrane irrespective of the type of solute, charge, solvent, and membrane.
- (3)
- Membrane fouling and membrane sensitivity towards chemicals such as chlorine, effects of temperature, and pH are not considered.
2.3. Steric Hindrance Pore Model (SHP)
3. Experimental Methods
4. Results and Discussion
4.1. Pure Water Permeability
4.2. Calculation of σ, Ps, and rp Based on the Spiegler–Kedem and SHP Models
4.3. Selection of NF Membranes for Smart Water Production Using a Predictive Model
4.3.1. Relating Lp with σ and Ps
- (1)
- Table 4 shows that HYDRACoRe 10 had poor ion separation. HYDRACoRe 50, made of sulfonated polyethersulfone, was not used to have comparable membrane materials for the model.
- (2)
- The Lp chosen for the plot to create the model was in the range required for smart water production. Pure water permeability higher than that of ESNA would have resulted in very low divalent ion rejection. Choosing a membrane with lower permeability than NANO-SW meant a tighter membrane leading to higher rejection for any flux and low recovery thereby increasing power consumption.
4.3.2. Correlations for the Determination of σ and Ps of a Polyamide Membranes
- (1)
- Using Equations (13)–(22), the model was run to predict σtheoretical and Ps,theoretical for two NF membranes with pure water permeabilities as in Table 5.
- (2)
- Flux for the above-mentioned NF membranes with seawater as feed was calculated using Equation (2). A random flux value at 12 bar was chosen for the model.
- (3)
- The values for σtheoretical and Ps,theoretical, and flux at 12 bar was substituted into Equations (5) and (6) to calculate the theoretical rejection (Rtheoretical).
- (4)
- To validate the calculated equations, ion rejection by the two chosen NF membranes was experimentally determined (Rexperimental) using Equation (1) for individual ions in seawater. These rejection values were plotted against the respective membrane flux values, and transport parameters were determined by fitting the values using the Spiegler–Kedem equation. Hence, σexperimental and Ps,experimental were determined.
5. Conclusions
Supplementary Materials
Author Contribution
Funding
Acknowledgment
Conflicts of Interest
References
- Austad, T. Water-based EOR in Carbonate and Sandstone: New Chemical Understanding of the EOR-Potential using “Smart water”. In Enhanced Oil Recovery Field Case Studies; Sheng, J., Ed.; Gulf Professional Publishing: Houston, TX, USA, 2013; pp. 301–335. [Google Scholar]
- Nair, R.R.; Protasova, E.; Strand, S.; Bilstad, T. Membrane performance analysis for smart water production for enhanced oil recovery in carbonate and sandstone reservoirs. Energy Fuels 2018, 32, 4988–4995. [Google Scholar] [CrossRef]
- Cheryan, M. Ultrafiltration and Microfiltration Handbook; CRC Pres: Boca Raton, FL, USA, 1998. [Google Scholar]
- Oatley-Radcliffe, D.; Walters, M.; Ainscough, T.J.; Williams, P.M.; Mohammad, A.W.; Hilal, N. Nanofiltration membranes and processes: A review of research trends over the past decade. J. Water Process. Eng. 2017, 19, 164–171. [Google Scholar] [CrossRef]
- Hilal, N.; Al-Zoubi, H.; Mohammad, A.; Darwish, N. Nanofiltration of highly concentrated salt solutions up to seawater salinity. Desalination 2005, 184, 315–326. [Google Scholar] [CrossRef]
- Gilron, J.; Gara, N.; Kedem, O. Experimental analysis of negative salt rejection in nanofiltration membranes. J. Membr. Sci. 2001, 185, 223–236. [Google Scholar] [CrossRef]
- Spiegler, K.; Kedem, O. Thermodynamics of hyperfiltration (reverse osmosis): Criteria for efficient membranes. Desalination 1966, 1, 311–326. [Google Scholar] [CrossRef]
- Kedem, O.; Katchalsky, A. Permeability of composite membranes: Part 1. Electric current, volume flow and flow of solutes through membranes. Trans. Faraday Soc. 1963, 59, 1918–1953. [Google Scholar] [CrossRef]
- Murthy, Z.; Gupta, S.K. Estimation of mass transfer coefficient using a combined nonlinear membrane transport and film theory model. Desalination 1997, 109, 39–49. [Google Scholar] [CrossRef]
- Jye, L.W.; Ismail, A.F. Nanofiltration Membranes—Synthesis, Characterization and Applications; CRC Press, Taylor & Francis Group: Boca Raton, FL, USA, 2017. [Google Scholar]
- Diwara, C.K.; Lo, S.; Rumeau, M.; Pontie, M.; Sarr, O. A phenomenological mass transfer approach in nanofiltration of halide ions for a selective defluorination of brackish drinking water. J. Membr. Sci. 2003, 219, 103–112. [Google Scholar] [CrossRef]
- Nakao, S.I.; Kimura, S. Models of membrane transport phenomena and their applications for ultrafiltration data. J. Chem. Eng. Jpn. 1982, 15, 200–205. [Google Scholar] [CrossRef]
- Wang, X.L.; Tsuru, T.; Togoh, M.; Nakao, S.I.; Kimura, S. Evaluation of pore structure and electrical properties of nanofiltration membranes. J. Chem. Eng. Jpn. 1994, 28, 186–192. [Google Scholar] [CrossRef]
- Bowen, R.; Mohammad, W.A. Diafiltration by Nanofiltration: Prediction and Optimization. AIChe J. 1998, 44, 1799–1812. [Google Scholar] [CrossRef]
- Hussain, A.; Nataraj, S.; Abashar, M.; Al-Mutaz, I.; Aminabhavi, T. Prediction of physical properties of nanofiltration membranes using experiment and theoretical models. J. Membr. Sci. 2008, 310, 321–336. [Google Scholar] [CrossRef]
- Luo, J.; Wan, Y. Effect of highly concentrated salt on retention of organic solutes by nanofiltration polymeric membranes. J. Membr. Sci. 2011, 372, 145–153. [Google Scholar] [CrossRef]
- Hilal, N.; Al-Zoubi, H.; Darwish, N.; Mohammad, A. Characterisation of nanofiltration membranes using atomic force microscopy. Desalination 2005, 177, 187–199. [Google Scholar] [CrossRef]
- Yaroshchuk, A. Negative rejection of ions in pressure-driven membrane processes. Adv. Colloid Interface Sci. 2008, 139, 150–173. [Google Scholar] [CrossRef] [PubMed]
- Nilsson, M.; Tragårdh, G.; Ostergren, K. The influence of pH, salt and temperature of nanofiltration performance. J. Membr. Sci. 2008, 312, 97–106. [Google Scholar] [CrossRef]
- Deshmukh, S.S.; Childress, A. Zeta potential of commercial RO membranes: Influence of source water type and chemistry. Desalination 2001, 140, 87–95. [Google Scholar] [CrossRef]
- Tansel, B. Significance of thermodynamic and physical characteristics on permeation of ions during membrane separation: Hydrated radius, hydration free energy and viscous effects. Sep. Purif. Technol. 2012, 86, 119–126. [Google Scholar] [CrossRef]







| Ions | Cl− | Na+ | SO42− | Ca2+ | Mg2+ |
|---|---|---|---|---|---|
| Stokes Radius (nm) | 0.121 | 0.184 | 0.231 | 0.310 | 0.348 |
| Membranes | HYDRACoRe10 | HYDRACoRe50 | NF 270 | SR 90 | ESNA | NANO-SW | LFC3 | HYDRApro501 |
|---|---|---|---|---|---|---|---|---|
| Material | Sulphonated Polyethersulfone | Composite Polyamide | ||||||
| pH range | 2–11 | 3–10 | 2–10 | 3–9 | 2–10.6 | 2–11 | ||
| Area (m2) | 2.3 | 2.6 | 2.3 | |||||
| Membranes | Pure Water (L m−2 h−1 bar−1) | Seawater (L m−2 h−1 bar−1) |
|---|---|---|
| HYDRACoRe 10 | 13.56 | 9.5 |
| ESNA | 10.52 | 7.9 |
| NF 270 | 9.38 | 6.1 |
| HYDRACoRe 50 | 5.15 | 3.8 |
| SR 90 | 4.46 | 3.3 |
| NANO-SW | 3.27 | 1.9 |
| LFC3 | 2.85 | - |
| HYDRApro 501 | 1.32 | - |
| Membranes | Ions | σ (−) | Ps (m s−1) | q | rp (nm) |
|---|---|---|---|---|---|
| ESNA | Cl− | 0.14 | 3.023 × 10−5 | 0.30 | 0.41 |
| Na+ | 0.14 | 1.701 × 10−5 | 0.29 | 0.63 | |
| SO42− | 0.66 | 6.211 × 10−6 | 0.69 | 0.34 | |
| Ca2+ | 0.29 | 1.953 × 10−5 | 0.44 | 0.71 | |
| Mg2+ | 0.24 | 1.26 × 10−5 | 0.40 | 0.86 | |
| NF 270 | Cl− | 0.18 | 2.105 × 10−5 | 0.34 | 0.35 |
| Na+ | 0.19 | 1.521 × 10−6 | 0.35 | 0.52 | |
| SO42− | 0.97 | 5.341 × 10−7 | 0.93 | 0.25 | |
| Ca2+ | 0.41 | 1.879 × 10−5 | 0.53 | 0.58 | |
| Mg2+ | 0.45 | 6.154 × 10−6 | 0.56 | 0.62 | |
| SR 90 | Cl− | 0.36 | 4.241 × 10−6 | 0.50 | 0.24 |
| Na+ | 0.25 | 7.313 × 10−6 | 0.41 | 0.45 | |
| SO42− | 0.99 | 4.859 × 10−7 | 0.96 | 0.24 | |
| Ca2+ | 0.82 | 1.474 × 10−6 | 0.79 | 0.39 | |
| Mg2+ | 0.92 | 3.276 × 10−7 | 0.85 | 0.41 | |
| HYDRACoRe10 | Cl− | −0.01 | −4.844 × 10−7 | - | - |
| Na+ | 0.03 | 3.115 × 10−5 | 0.13 | 1.42 | |
| SO42− | 0.16 | 1.728 × 10−5 | 0.32 | 0.73 | |
| Ca2+ | 0.15 | 7.254 × 10−5 | 0.31 | 0.99 | |
| Mg2+ | 0.05 | 5.447 × 10−5 | 0.16 | 2.15 | |
| HYDRACoRe50 | Cl− | 0.17 | 1.329 × 10−5 | 0.33 | 0.37 |
| Na+ | 0.24 | 1.538 × 10−5 | 0.40 | 0.46 | |
| SO42− | 0.67 | 3.849 × 10−6 | 0.70 | 0.33 | |
| Ca2+ | 0.32 | 5.928 × 10−6 | 0.47 | 0.67 | |
| Mg2+ | 0.38 | 1.417 × 10−5 | 0.51 | 0.68 | |
| NANO-SW | Cl− | 0.37 | 9.045 × 10−7 | 0.50 | 0.24 |
| Na+ | 0.29 | 4.439 × 10−6 | 0.44 | 0.42 | |
| SO42− | 0.99 | 3.298 × 10−8 | 0.96 | 0.24 | |
| Ca2+ | 0.88 | 2.171 × 10−6 | 0.84 | 0.37 | |
| Mg2+ | 0.93 | 3.471 × 10−7 | 0.88 | 0.40 |
| Pure Water Permeability, m s−1 Pa−1 | Flux at 12 bar, m s−1 | Ions | σtheoretical | σexperimental | Ps,theoretical, m s−1 | Ps,experimental, m s−1 | Rtheoretical | Rexperimental |
|---|---|---|---|---|---|---|---|---|
| 2.56 × 10−11 | 2.06 × 10−5 | Cl− | 0.22 | 0.18 | 1.44 × 10−5 | 2.11 × 10−5 | 0.16 | 0.11 |
| Na+ | 0.18 | 0.19 | 1.52 × 10−5 | 1.52 × 10−5 | 0.13 | 0.14 | ||
| SO42− | 0.83 | 0.97 | 1.99 × 10−6 | 5.34 × 10−7 | 0.79 | 0.96 | ||
| Ca2+ | 0.37 | 0.41 | 1.82 × 10−5 | 1.88 × 10−5 | 0.23 | 0.24 | ||
| Mg2+ | 0.44 | 0.45 | 6.27 × 10−6 | 6.15 × 10−6 | 0.42 | 0.41 | ||
| 1.24 × 10−11 | 8.90 × 10−6 | Cl− | 0.35 | 0.36 | 1.23 × 10−6 | 4.24 × 10−6 | 0.35 | 0.29 |
| Na+ | 0.26 | 0.25 | 7.28 × 10−6 | 7.31 × 10−6 | 0.17 | 0.16 | ||
| SO42− | 0.99 | 0.99 | 2.18 × 10−7 | 4.86 × 10−7 | 0.97 | 1.00 | ||
| Ca2+ | 0.76 | 0.82 | 4.99 × 10−6 | 1.47 × 10−6 | 0.53 | 0.75 | ||
| Mg2+ | 0.89 | 0.92 | 7.44 × 10−7 | 3.28 × 10−7 | 0.85 | 0.96 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nair, R.R.; Protasova, E.; Strand, S.; Bilstad, T. Implementation of Spiegler–Kedem and Steric Hindrance Pore Models for Analyzing Nanofiltration Membrane Performance for Smart Water Production. Membranes 2018, 8, 78. https://doi.org/10.3390/membranes8030078
Nair RR, Protasova E, Strand S, Bilstad T. Implementation of Spiegler–Kedem and Steric Hindrance Pore Models for Analyzing Nanofiltration Membrane Performance for Smart Water Production. Membranes. 2018; 8(3):78. https://doi.org/10.3390/membranes8030078
Chicago/Turabian StyleNair, Remya R., Evgenia Protasova, Skule Strand, and Torleiv Bilstad. 2018. "Implementation of Spiegler–Kedem and Steric Hindrance Pore Models for Analyzing Nanofiltration Membrane Performance for Smart Water Production" Membranes 8, no. 3: 78. https://doi.org/10.3390/membranes8030078