3.2. Comparative Study between the Conventional Cyclonic Separator and the Cyclonic Filter Separator
Figure 4 shows the streamlines of the oil and water phases in the filtering and conventional hydrocyclones. An analysis of this figure shows the presence of two distinct fluid streams: a descending spiral shape, close to the wall, and an ascending spiral in the central region. Similar behaviors were found in the literature on conventional hydrocyclones, as in the works reported by [
3,
5,
8,
10,
26,
27,
28,
29,
30]. This behavior was associated with the difference in density, where the spiral flow of the continuous phase (water) tends to flow closer to the separator wall, while the stream of the dispersed phase (oil) flows inside the separator.
The phase’s behavior is maintained until the end of the process, thus allowing an ideal collection of fluids in the oil and water outlets. However, when comparing the devices formed without or with the porous conical wall (
Figure 4a,b) it can be observed that the oil stream in the center of the separator shows an unstable behavior of the oil core when compared to the cyclonic separator, without the porous conical wall. This fact can be explained by the presence of the permeate flux perpendicular to the ceramic membrane. However, it can be seen with the help of
Figure 4c,d that the behavior of the collection of fluids in the outlet region of the cyclonic separators is not altered.
Figure 5 illustrates the pressure distributions along the xy and xz longitudinal planes. Note that the pressure decreases radially towards the center from the separator wall, reaching its lowest value close to the outlets. A dimilar behavior was observed in ref. [
3,
4,
8] when studying traditional hydrocyclones, and in ref. [
5] with a geometry similar to that of the present research, considering the impermeable conical wall. This behavior is associated with the centrifugal force.
When comparing the cyclonic separators without and with the ceramic membrane (
Figure 5a,b, respectively), it was observed that, with the same feeding speed, the pressure gradient in the vicinity of the cylindrical and conical walls was less intense for the filtering cyclonic separator than it was for the equipment without the ceramic membrane (conventional cyclonic separator). Similar behavior was also obtained by [
31] when studying a filtering hydrocyclone in the solid particle/water separation process. The lower intensity of the pressure gradient in the filtering separator is because the pores of the membrane represent an additional outlet of liquid, previously not available during the operation of the conventional cyclonic separator (where water necessarily had to escape through the underflow holes or overflow). This fact can also be seen in
Figure 6, which presents the pressure profiles in the axial positions y = 0.15 m, y = 0.45 m and y = 0.75 m along the separators.
The tangential velocity field on the yz plane, passing through the central axis of the cyclonic separator, is shown in
Figure 7. It appears that the tangential velocity increases in intensity radially in the direction of the central axis (zero velocity) for the cylindrical and conical walls of the evaluated devices, reaching maximum values in the vicinity of the cyclonic separator walls. A similar behavior is reported in [
4,
5,
11,
32,
33,
34]. However, when comparing the separators without and with the ceramic membrane, the influence of the permeate flux through the ceramic membrane on the hydrodynamic behavior of the components of tangential velocities is perceived. This behavior is confirmed in
Figure 8, which describes the tangential velocity profiles.
The axial velocity field on the yz plane, passing through the central axis of the cyclonic separator, is shown in
Figure 9. In general, it is observed that the axial velocity components increase as they approach the oil and water outlets, and have the highest intensities in the vicinity of the separator axis. Similar behavior was observed in [
5] when similarly evaluating a device. However, the presence of the ceramic membrane leads to the disorderly character of the behavior, as compared to the cyclonic separator with an impermeable wall (conventional cyclonic separator).
It is possible to observe in
Figure 10, which describes the axial velocity profile at positions y = 0.15 m, y = 0.45 m and y = 0.75 m, that the filtration phenomena modified the axial velocity profiles in the cyclonic separator.
It appears that the filtering cyclonic separator has higher axial speeds in the central region of the equipment when compared with the cyclonic separator with an impermeable wall. It can also be observed that the highest values obtained for axial speed are located at the end of the equipment (close to the exits). This is because, in that region, the axial linear momentum prevails over the angular momentum, thus reducing the intensity of the turbulence, especially in the vicinity of the oil and water outlets. This behavior was also observed by [
4,
35].
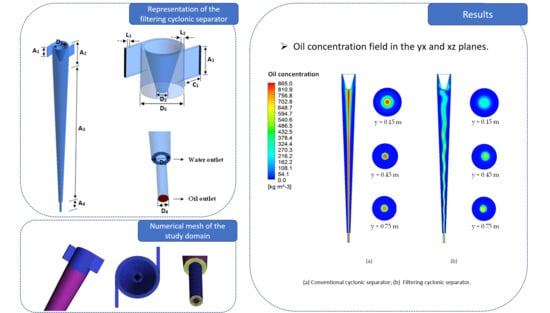
Figure 11 illustrates the oil concentration field on the xy and xz planes passing through the central axis of the conventional and filtering cyclonic separators at different transversal positions. It is possible to observe that the oil tends to be located in the center of the separator from the beginning of the flow in the two devices, as already observed in the streamlines. However, the behavior of the oil in the central region of the filtering cyclonic separator changes, forming a more diluted and undulating oil stream. This fact can be explained by the change in the fluid dynamic behavior of the fluids due to the presence of the permeate flux perpendicular to the ceramic membrane, as well as the increase in the axial speed of the water observed in
Figure 9 and
Figure 10.
The oil concentration profiles represented in
Figure 12 confirm that the oil concentration is lower in the cyclonic separator with a ceramic membrane. This fact is due to the migration of water in the direction of the conical wall of the equipment, which causes the oil stream to disperse and suffer a greater effect from the mixture of fluids.
Figure 12 also shows the oil concentration profiles for the cyclonic separators with and without the ceramic membrane close to the conical wall (region highlighted in
Figure 12), calculated in the axial positions of 0.15 m, 0.45 m and 0.75 m. It is possible to observe, in
Figure 12a, a greater concentration of oil in the cyclonic separator without a ceramic membrane (conventional hydrocyclone), as had already been observed along the axial position. However, the different behaviors of the oil concentration profiles in the vicinity of the conical wall are observed in
Figure 12c, in the region close to the outlets, as a result of the greater flux of water allowed by the membrane pores in this region, which causes an increase in the oil concentration for the equipment with an impermeable wall (filtering cyclonic separator), a fact that interferes in the fluid separation efficiency, which will be discussed in detail later.
Table 5 shows the inlet and outlet mass flow rate for each fluid in the conventional and filtering cyclonic separators. It is possible to observe that the water mass flow rate at the axial outlet of the filtering cyclonic separator decreased when compared to the conventional cyclonic separator. This fact occurs due to the permeate flux leaving the membrane and due to the increase in the oil concentration close to the concentrate outlet. We state that the permeate flux (0.74 kg/s, almost 10.71% of the feed flow rate) corresponds to clean water since the membrane rejection index is unified. This is very important from the social point of view, and shows clearly the impact of this research on the world.
Table 6 shows the total separation efficiency, liquid ratio and reduced separation efficiency of the conventional cyclonic separator and the filtering cyclonic separator. It is possible to observe that the filtration associated with the separation process was able to modify the liquid ratio, which was increased concerning the conventional cyclonic separator.
It is believed that the migration of the suspension stream in the direction of the wall caused interference in the relationships between the volumes of the free and forced vortexes, which, due to the turbulence generated, collaborated in the modification of the liquid fraction that was directed to each of the exits. It should also be noted that the calculation of the reduced separation efficiency in the filtering cyclonic separator does not take into account the permeate flux, which, due to the additional flow, minimizes the reduced separation efficiency. A similar fact was observed in [
1,
36], when studying numerically and experimentally the optimization of the separation processes in filtering hydrocyclones.
Under the same operational conditions, the total efficiency and reduced efficiency of the filtering cyclonic separator suffered a decrease of approximately 5%, when compared to the cyclonic separator without the presence of the porous medium (conventional hydrocyclone). This difference is attributed to the way these parameters are calculated. It is possible to observe, through the tangential velocity profiles, that the fluid has been dampened in the rotational movement inside the separator. As the fluid’s spiral movement decreases, the centrifugal force inside the equipment is reduced, which leads to the least amount of particles collected. This leads to an increase in the oil concentration close to the membrane, which can induce the formation of the polarization concentration layer.
From the petroleum industry point of view, oil production has increased considerably throughout the world over the years. As a result, the search for new types/processes of produced water treatment (that is associated with that of oil production) has become crucial. These new alternatives take into account factors as diverse as the forms of oil in water (free, emulsified, and/or dissolved), the destination of treated water (disposal, injection and/or reuse), the location of the production equipment/facilities, the legislative, technical and financial feasibility of the process and equipment involved, as well as the availability of the infrastructure.
In the case of international legislation (present day) for the disposal of production water at sea, the maximum limits for total oils and greases vary from 15 mg·L
−1 to 50 mg·L
−1, depending on the country. In Brazil, the permitted value is 29 mg·L
−1 (simple monthly arithmetic mean), with a maximum daily value of 42 mg·L
−1 [
37]. To comply with environmental legislation, the oil industry has used certain equipment, such as air floats, hydrocyclones (offshore installations), bed coalescers, and gravitational separators (onshore installations). Despite being used today, these processes have some disadvantages, such as long residence time, the use of high-cost special chemicals, the generation of solid waste, and their low efficiencies, especially when the oil drops have diameters in the order of micrometers, and tensioactive agents are present, which are very common in emulsions.
For more severe conditions (small oil droplets and emulsified oil), the membrane separation process has been used. As advantages of this technique, we can mention the retention of oil drops with dimensions smaller than 10 µm, the low operating cost when compared to usual processes, the rendering as unnecessary the use of chemicals, and the ability to generate permeates with acceptable quality (complying with current environmental legislation). Despite these advantages, during operation, there is a rapid decline in the permeate flow, which is mainly attributed to the concentration polarization and fouling phenomena.
Concentration polarization consists of the formation of a concentration gradient in the fluid layer immediately adjacent to the membrane surface (concentration boundary layer). Fouling, on the other hand, is related to the blocking of the membrane pores by oil drops and other contaminants present in the produced water, and the accumulation of particles on the membrane surface (deposition, precipitation and adsorption), which cause an increase in operating pressure (transmembrane pressure), a reduction in the facility’s efficiency, and a reduction in the membrane life. In industry, the concentration polarization effect is controlled by increasing the speed of the mixture in the feed (increased fluid turbulence) or air bubbling. Fouling, on the other hand, is controlled by pre-treating the feed stream, changing the operating conditions, cleaning the membranes (chemical and physical), and even modifying the membranes.
Given the above, it can be said that the application of a filtering hydrocyclone presents itself as a very robust alternative to replace or even operate in conjunction with existing traditional systems. The main advantages of the proposed equipment are related to those of conventional hydrocyclones and membranes; for example, the low operating and maintenance cost, the fact that it does not require the use of chemicals as inputs, as well as the high quality of the permeate, which complies with current legislation. Despite this, new studies are needed to better understand the process and equipment, which will make it possible to expand/optimize their application in the treatment of water polluted by oil and/or other contaminants. The main challenges are related to operational problems, mainly those resulting from the phenomena of concentration polarization and fouling in the membrane, and the geometric and thermo-fluid dynamic of the hydrocyclone, which strongly affect the separation efficiency.