Solitonic Windkessel Model for Intracranial Aneurysm
Abstract
:1. Introduction
2. Theoretical Model
2.1. The Five-Element Windkessel Model
2.2. Solitonic Modeling in Some Specific Cases
3. Method
4. Results
5. Discussion
5.1. Rupture Caused by the Size of Aneurysm
5.2. Rupture Caused by the Formation of Daughter Aneurysm
5.3. Rupture Caused by the Compliance of Aneurysm
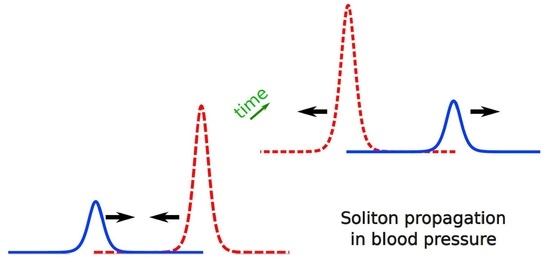
5.4. Rupture Caused by Soliton Propagation
5.5. Rupture Caused by the Large Amplitude “to-and-fro” Oscillation
6. Conclusions
- The formation of a large aneurysm with an aspect ratio larger than 1.6;
- The formation of the daughter aneurysm as large as the mother aneurysm;
- The formation of a spherical-shaped aneurysm with large compliance.
- It is a non-decaying soliton propagation arising from small compliance;
- There is a “to-and-fro” large amplitude resonating oscillation arising from large compliance.
- (i)
- Aneurysm with an aspect ratio larger than 1.6 (cf. Section 5.1);
- (ii)
- Aneurysm with a thin or elastic blood wall, where the elastic situation sometimes happens to young patients (cf. Section 5.3);
- (iii)
- Dumbbell-shaped aneurysm with its daughter size as large as 80% of the mother aneurysm (cf. Section 5.2);
- (iv)
- Dumbbell aneurysms, especially the daughter aneurysm, with a thick or inelastic blood wall, possibly experience the soliton propagation. It explains that the formation of the daughter aneurysm itself is dangerous (cf. Section 5.4)
- (v)
- Dumbbell-shaped aneurysms with thin or elastic blood wall possibly experience the to-and-fro large amplitude resonating oscillation. This explains that the rapture can take place by even a small daughter aneurysm formation (cf. Section 5.5).
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Crompton, M.R. Mechanism of growth and rupture in cerebral berry aneurysms. Br. Med. J. 1966, 1, 1138–1142. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Dumount, A.S.; Lanzino, G.; Kassel, N.F. Unruptured aneurysms. J. Neurosurg. 2002, 96, 52–56. [Google Scholar] [CrossRef] [PubMed]
- Bender, B.T.; Wendt, H.; Monarch, T.; Beaty, N.; Lin, L.M.; Huang, J.; Coon, A.; Tamargo, R.J.; Colby, G.P. Small aneurysms account for the majority and increasing percentage of aneurysmal subarachnoid hemorrhage: A 25-years, single institution study. Neurosurgery 2018, 83, 692–699. [Google Scholar] [CrossRef] [PubMed]
- Ujiie, H.; Tachibana, H.; Hiramatsu, O.; Hazel, A.L.; Matsumoto, T.; Ogasawara, Y.; Nakajima, H.; Hori, T.; Takakura, K.; Kajiya, F. Effect of size and shape (aspect ratio) on the hemodynamics of saccular aneurysms: A possible index for surgical treatment of intracranial aneurysms. Neurosurgery 1999, 45, 119–130. [Google Scholar]
- Ujiie, H.; Tamano, H.; Sasaki, K.; Hori, T. Is the aspect ratio a reliable index for predicting the rupture of a saccular aneurysm? Neurosurgery 2001, 48, 495–503. [Google Scholar] [CrossRef]
- Ujiie, H.; Liepsch, D.W.; Goetz, M.; Yamaguchi, R.; Yonetani, H.; Takakura, K. Hemodynamic study of the anterior communicating artery. Stroke 1996, 27, 2086–2094. [Google Scholar] [CrossRef]
- Liepsch, D.W.; Steiger, H.J.; Poll, A.; Reulen, H.J. Hemodynamic stress in lateral saccular aneurysms. Biorheology 1987, 24, 689–710. [Google Scholar] [CrossRef]
- Steiger, H.J. Pathophisiology of development and rupture of cerebral aneurysms. Acta Neurochir. Suppl. 1990, 48, 1–57. [Google Scholar]
- Tamano, Y.; Ujiie, H.; Yosimoto, S.; Hori, T. Rheological characteristics of the aneurysm at the middle cerebral artery bifurcation. Noshinkeigeka 2001, 29, 921–930. [Google Scholar]
- Firouzian, A.; Manniesing, R.; Metz, C.T.; Risselada, R.; Klein, S.; Kooten, F.; Sturkenboom, M.C.J.M.; Lugt, A.; Niessen, W.J. Quantification of intracranial aneurysm morphodynamics from ECG-gated CT angiography. Acad. Radiol. 2013, 20, 52–58. [Google Scholar] [CrossRef]
- Omodaka, S.; Endo, H.; Niizuka, K.; Fujimura, M.; Endo, T.; Sato, K.; Sugiyama, S.I.; Inoue, T.; Tominaga, T. Circumferential wall enhancement on magnetic resonance imaging is useful to identify rupture site in patients with multiple cerebral aneurysms. Neurosurgery 2018, 82, 638–644. [Google Scholar] [CrossRef] [PubMed]
- Backs, D.; Hendrickse, J.; Schaaf, I.; Algra, A.; Lindgren, A.E.; Verweij Rinkel, G.J.; Vergouwen, M.D.I. Determinants of gadolinium-enhancement of the aneurysm wall in unruptured intracranial aneurysms. Neurosurgery 2018, 83, 719–725. [Google Scholar] [CrossRef] [PubMed]
- Kallmes, D.F. Point: CFD-Computational fluid dynamics or confounding factor dissemination. AJNR Am. J. Neuroradiol. 2012, 33, 395–396. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Shojima, M.; Oshima, M.; Takagi, K.; Torii, R.; Nagata, K.; Shirouzu, I.; Morita, A.; Kirino, T. Role of bloodstream impacting force and the local pressure elevation in the rupture of cerebral aneurysms. Stroke 2005, 36, 1933–1938. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ogawa, Y.; Nakahara, T.; Nishida, Y.; Kobayashi, C.; Hirata, T.; Nagano, H.; Shiratori, S.; Shimano, K. In vitro measurement of platelet adhesion to intact endothelial cells under low shear conditions. Biorheology 2018, 54, 51–65. [Google Scholar] [CrossRef] [PubMed]
- Tulamo, R.; Froesen, J.; Hernesniemi, J.; Niemela, M. Inflammatory changes in the aneurysm wall: A review. J. Neurointervent. Surg. 2010, 2, 120–130. [Google Scholar] [CrossRef]
- Otto, F. Die Grundform des arteriellen Pulses. Z. Fur Biol. 1899, 37, 483–526. [Google Scholar]
- Westrhof, N.; Lankhaar, J.W.; Westerhof, B.E. The arterial Winfkessel. Med. Biol. Eng. Comput. 2009, 47, 131–141. [Google Scholar] [CrossRef] [Green Version]
- Russell, J.S. On certain effects produced on sound by the rapid motion of the observer. Rep. Eighteenth Meet. Br. 1848. [Google Scholar]
- Korteweg, D.J.; Vries, G. On the change of form of long waves advancing a rectangular canal, and on a new type of long stationary waves. Philos. Mag. 1895, 39, 422–443. [Google Scholar] [CrossRef]
- Zabusky, N.J.; Kruskal, M.D. Interaction of “Solitons” in a collisionless plasma and the recurrence of initial states. Phys. Rev. Lett. 1965, 15, 240. [Google Scholar] [CrossRef] [Green Version]
- Scott, W.; Chu, F.Y.; Machlaughlin, D.W. The soliton: A new concept in applied science. Proc. IEEE 1973, 61, 1443. [Google Scholar] [CrossRef]
- Lamb, G.L., Jr. Elements of Soliton Theory; John Wily and Sons: New York, NY, USA, 1980. [Google Scholar]
- Iwata, Y. Energy-dependent existence of soliton in the synthesis of chemical elements. Mod. Phys. Lett. A 2015, 30, 1550088. [Google Scholar] [CrossRef] [Green Version]
- Iwata, Y.; Stevenson, P. Conditional recovery of time-reversal symmetry in many nucleus systems. New J. Phys. 2019, 21, 043010. [Google Scholar] [CrossRef]
- Iwata, Y. Solitons in nuclear time-dependent density functional theory. Front. Phys. 2020, 8, 154. [Google Scholar] [CrossRef]
- Toda, M. Vibration of a chain with non-linear interaction. J. Phys. Soc. Jpn. 1967, 22, 431–436. [Google Scholar] [CrossRef]
- Toda, M. Wave propagation in anharmonic lattices. J. Phys. Soc. Jpn. 1967, 23, 501–506. [Google Scholar] [CrossRef]
- Toda, M. Mechanics and statistical mechanics of nonlinear chains. J. Phys. Soc. Jpn. 1969, 26, 235–237. [Google Scholar]
- Hirota, R.; Suzuki, K. Studies on lattice solitons by using electrical circuit. J. Phys. Soc. Jpn. 1970, 28, 1366–1367. [Google Scholar] [CrossRef]
- Henon, M. Integrals of the Toda lattice. Phys. Rev. 1974, B9, 1921–1924. [Google Scholar] [CrossRef]
- Wiebers, D.O.; Whisnant, J.P.; Sundt, T.M.; O’Fallen, W.M. The significance of unruptured intracranial saccular aneurysms. J. Neurosurg. 1987, 66, 23–29. [Google Scholar] [CrossRef] [PubMed]
- Ishida, F.; Ogawa, H.; Simizu, T.; Kojima, T.; Taki, W. Visualizing the dynamics of cerebral aneurysms with four-dimensional computed tomographic angiography. Neurosurgery 2005, 57, 460–471. [Google Scholar] [CrossRef] [PubMed]
- Hayakawa, M.; Maeda, S.; Sadato, A.; Tanaka, T.; Kaito, T.; Hattori, N.; Ganaha, T.; Moriya, S.; Katada, K.; Murayama, K.; et al. Detection in ruptured and unruptured cerebral aneurysms by electrocardiographically gated 3-demensional computed tomographic angiography with a 320-row area detector computed tomography and evaluation of its clinical usefulness. Neurosurgery 2011, 69, 843–851. [Google Scholar] [CrossRef] [PubMed]
- Maslehaty, H.; Ngando, H.; Meila, D.; Brassel, F.; Scholz, M.; Petridis, A.K. Estimated low risk of rupture of small-sized unruptured intracranial aneurysms (UIAs) in relation to intracranial aneurysms in patients with subarachnoid haemorrhage. Acta Neurochir. 2013, 155, 1095–1100. [Google Scholar] [CrossRef]
- Wiebers, D.O.; Whisnant, J.P.; Huston, J., 3rd; Meissner, I.; Brown, R.D., Jr.; Piepgras, D.G.; Forbes, G.S.; Thielen, K.; Nichols, D.; O’Fallon, W.M.; et al. International study of unruptured intracranial aneurysms investigators: Unruptured intracranial aneurysms: Natural history, clinical outcome, and risks of surgical and endovascular treatment. Lancet 2003, 362, 103–110. [Google Scholar] [CrossRef]
- UCAS Japan Investigators; Morita, A.; Kirino, T.; Hashi, K.; Aoki, N.; Fukuhara, S.; Hashimoto, N.; Nakayama, T.; Sakai, M.; Teramoto, A.; et al. The natural course of unruptured cerebral aneurysms in a Japanese cohort. N. Engl. J. Med. 2012, 366, 2474–2482. [Google Scholar]
- Cornelissen, B.M.W.; Schneiders, J.J.; Potters, W.V.; van den Berg, R.; Velthuis, B.K.; Rinkel, G.J.E.; Slump, C.H.; Van Bavel, E.; Majoie, C.B.L.M.; Marquering, H.A. Hemodynamic differences in intracranial aneurysms before and after rupture. Am. J. Neuroradiol. 2015, 36, 1927–1933. [Google Scholar] [CrossRef] [Green Version]






| Beat [bpm] | Artery Blood Flow [mL/min] | |
|---|---|---|
| Typical values | 70 (40–110) | 50 (40–60) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ujiie, H.; Iwata, Y. Solitonic Windkessel Model for Intracranial Aneurysm. Brain Sci. 2022, 12, 1016. https://doi.org/10.3390/brainsci12081016
Ujiie H, Iwata Y. Solitonic Windkessel Model for Intracranial Aneurysm. Brain Sciences. 2022; 12(8):1016. https://doi.org/10.3390/brainsci12081016
Chicago/Turabian StyleUjiie, Hiroshi, and Yoritaka Iwata. 2022. "Solitonic Windkessel Model for Intracranial Aneurysm" Brain Sciences 12, no. 8: 1016. https://doi.org/10.3390/brainsci12081016