Evaluation of Sensitivity and Calibration of the Chaboche Kinematic Hardening Model Parameters for Numerical Ratcheting Simulation

Abstract

Ratcheting failure of materials and structures subjected to low cycle fatigue in the presence of significant mean stress is of great interest to researchers. In this experimental and numerical study, the response of 316L stainless steel samples was observed in symmetric strain control uniaxial test followed by post-stabilized monotonic test, uniaxial and biaxial ratcheting tests, in order to determine the Chaboche model parameters and to evaluate ratcheting prediction using finite element analysis. The critical elastic limit was initially obtained from incremental uniaxial cyclic tests. The Chaboche parameters were subsequently extracted from experimental hysteresis and post-stabilized monotonic stress plastic-strain curves using two optimization technics, namely, the Particle Swarm Optimization (PSO) and Genetic Algorithm (GA). The two optimization methods were compared for efficiency, in terms of time and accuracy. The PSO method presented higher efficient results and was subsequently used to derive the parameters from hysteresis and post-stabilized monotonic curves. Different values (by definition) of elastic limit were also used. The Finite Element commercial software ANSYS was utilized with the Chaboche model to predict the uniaxial and biaxial ratcheting behavior of 316L stainless steel pipe. The comparison between experimental and the numerical simulation demonstrates that adopting post-stabilized monotonic curve rather than hysteresis curve and with accurate elastic limit obtained from incremental loading test improves ratcheting prediction significantly.

1. Introduction

Load-bearing engineering components are frequently exposed to random loading and the risk of occurrence of ratcheting is increased significantly [1,2,3,4,5]. Offshore structures, pressure vessels and piping system, structures operating in earthquake zones, airplane landing gears and nuclear reactors are typical examples of such components and structures [6,7,8]. Structures subjected to stress cycles beyond the elastic limit oblige a trustworthy design, especially in the presence of a significant mean stress from loads such as dead weight or internal pressure [1,6,9,10].

In researches on ratcheting behaviour, bilinear kinematic hardening (BKH), multilinear kinematic hardening (MKIN) [11] and the nonlinear kinematic hardening (NLK) model developed by Chaboche [12] are commonly used, and are currently incorporated in commercial finite element programs such as ANSYS and ABAQUS [13]. Among the available models in commercial software, the Chaboche model is the most powerful [14]. However, this model overpredicts ratcheting strain under either uniaxial or multiaxial loading when compared with experimental results [13,15,16,17].

A solution to the above problem is found by identifying new material parameters [18] or using a more multifaceted material model [19,20]. However, implementation of more robust complex models can be time-consuming and complicated [15,21]. Kalnins reiterated the parameter identification for the material under consideration as an essential prerequisite for using an NLK model [22]. Accordingly, the dedicated method to figure out the best set of ratcheting parameters can extremely affect the result of ratcheting prediction.

Bari et al. proposed a methodical step-by-step concept for specifying the Chaboche model’s parameters. In their concept, the parameters were specified via numerical simulation of a hysteresis lower or upper curve [11,23,24]. The manual method to determine parameter values might be lengthy and time consuming, requiring numerous trial-and-error iterations for determining a set of parameters values. Rahman et al. evaluated the use of heuristic search techniques, such as the genetic algorithm, in automating the parameter value determination of developed models, and thus overcoming the limitations involved in manual calibration [25,26]. Two approaches to determine Chaboche model parameters are used by Kalnins et al. [22], namely the manual method and the numerical method, which make use of ABAQUS. They presented practicable applications of the Chaboche model in elastic-plastic ratcheting analysis.

Cyclic hardening can have a strong influence on the rate of ratcheting in unsymmetrical stress cycling [25,26]. In an effort to reduce the hardening-ratcheting coupling, they stabilized the hardening of the test specimens by axial symmetric strain cycling in the range of stress-strain similar to the following ratcheting tests. The positive or negative segment of the last saturated cycle of hysteresis curve was adopted in calculating the ratcheting parameters. However, Kalnins et al. adopted the monotonic stress-strain curve, instead of a hysteresis curve, obtained from a specimen subjected to unidirectional tension loading, to calibrate the ratcheting parameters [22]. The authors suggested that adopting the monotonic curve data for determining is predictable to present stuffy assessment of ratcheting that could be assumed suitable for design targets. They argued that for the case of stainless steel, the stress flow increases with additional cycles, more than that of the initial monotonic curve (initial half-cycle).

The ratcheting parameters are significantly sensitive to the elastic limit stress at which yielding instigates [22,27]. Precise application of elastic theory that causes a slight amount of nonlinear recovery was addressed [28]. From Table Y-2 of Section II, Part D, in ASME B&PV Code [29] and the Nuclear Safety Standards Commission document, KTA 3201.2, Table 7.7-8 13 [22], the elastic limit for stainless steels is assumed to be 0.55 times the elastic limit coefficient, which is either the Yield Strength Sy or the 0.2% strain offset. Zhou et al. proposed the elastic limit to be 0.54 times the 0.2% strain offset for 316L stainless steel [30]. The methods mentioned by Zhou considered the elastic limit for non-stabilized materials only, whereas other researchers found that the elastic limit coefficient is enlarged following stabilization hardening.

In this study, elastic limit and ratcheting behaviour of straight 316L austenitic stainless steel pipes subject to uniaxial and biaxial quasi-static cyclic loading are investigated experimentally. The elastic limit is obtained from incremental uniaxial cyclic tests but other elastic limits are evaluated (due to different definition of elastic limit) for ratcheting evaluation. Intelligent optimization techniques namely, Particle Swarm Optimization (PSO) and Genetic Algorithm (GA) methods are employed and compared with the objective to identify and calibrate the ratcheting parameters from monotonic and hysteresis curves.

2. Determination of Chaboche Material Parameters

2.1. Material and Specification

The pipe material 316L austenitic stainless steel is commonly used in the oil and gas industry. Its specification and chemical composition obtained by the Glow Discharge Spectrometry (GDS) test are listed in

Table 1. Chemical composition (%).

C	Mn	P	Co	Si	Cr	Ni	Mo	Ti	Al	V	Zr	N	Nb
0.0314	1.53	0.0378	0.373	0.365	16.4	11.4	2.14	0.007	0.004	0.074	0.018	0.104	0.01

, and the basic mechanical properties are listed in

Table 2. Basic mechanical properties.

${\mathit{\sigma }}_{\mathit{y}} \left(\mathbf{MPa}\right) (\mathbf{Offset} 0.2\%)$	${\mathit{\sigma }}_{\mathit{U}} \left(\mathbf{MPa}\right)$	E (GPa)
264	601	172

, in which ${\sigma }_y$ denotes 0.2% proof stress, ${\sigma }_U$ the ultimate stress and E the elastic modulus.

2.2. Specimen Preparation

The 316L austenitic stainless steel seamless pipes that were procured for ratcheting analysis measures an outer diameter of 60.3 mm and wall thickness of 3.9 mm. From these pipes, pipe test specimens were prepared by turning the test area to a smaller diameter, welding of end caps for both uniaxial and biaxial test specimens and drilling of pressurizing oil ports for biaxial specimens. The pipe test specimens were to be used for monotonic, uniaxial and biaxial tests and have geometry similar to those used in cyclic tests carried out by Jiao and Paquette et al. [31,32,33]. The gaged area was tapered to a smaller diameter to minimize the effect of thickness discontinuity on stresses. A finite element analysis of an exact model was run to confirm that the taper has an insignificant effect on the uniaxial loading stress of the tube at its mid length.

Figure 1 shows the dimension of the pipe specimen. The dimensions of the specimens were kept the same for both the uniaxial and biaxial test specimens. The overall specimen length was 260 mm and 290 mm for uniaxial and biaxial specimens, respectively, with the following variations in dimensions:

The diameter of the ends of the specimens was maintained as-received. For uniaxial test samples, the length of the ends is 40 mm. For biaxial test samples, the ends are 80 mm long in order to cater to pressurizing oil ports. The diameter of the middle gaged test section was machined down, using Computer Numerical Control (CNC) machine, to 1.44 mm wall thickness. The test section is 32 mm long. The linear tapers are 55 mm long. Special care was taken in the machining process to reduce changes in the physical surface and material properties of the specimens.

Steel caps were designed and fabricated to fit onto the ends of the pipe specimens. The end caps were screwed and then welded, using gas tungsten arc welding (GTAW), onto the ends of the pipe specimens in order to eliminate axial free play from the thread fastening system. The other sides of the end caps have thread connections designed to fit to the actuator of the universal testing machine. A nut tightening system was used to eliminate thread clearance, which might otherwise cause impact loading to the specimen when alternating between tension and compression loadings. For the biaxial test samples, a socket was welded onto an end cap for the supply of pressurizing oil. The quality of welding was assured by performing Dye Penetrant Inspection (DPI) test on test specimens. Finally, the specimens were heat treated, which involved heating at 900 °C for 1 h in a furnace and allowed to cool in air. The heat treatment reduces the effect of mechanical work from the manufacturing and machining processes and relaxes residual stresses due to welding of the caps. Figure 2 and Figure 3 show the geometry of the specimens.

2.3. Experimental Setup

The experiments were conducted on INSTRON 5982 universal testing machine. The machine provides the capability of testing under load or displacement control. The load readout from the Instron was monitored by another calibrated load cell, which was synced with a digital high speed data logger. The strains were measured using high elongation single element strain gauges for monotonic and uniaxial test samples and 90° 2-element strain rosettes for the biaxial test. The gauges were bonded to opposite sides of the test specimens to eliminate bending effects. The strains and loads were monitored and stored continuously by the data logger. The rate of loading was set at 0.75 mm/min and the stress-strain data stored at time intervals of 0.5 s. The data combination of force from the designed load cell and extension reading from the Instron machine was employed to monitor the force-displacement response of test specimens and not for numerical analysis because these data lack accuracy. The setup of the test system is shown in Figure 4 and Figure 5.

Advanced ratcheting analysis began with Rahman et al. who concluded that cyclic hardening could have a significant effect on ratcheting rate in unsymmetrical stress cycling [25]. Hence, in the present study, all monotonic, uniaxial and biaxial test specimens were cyclically stabilized through uniaxial symmetric strain cycling in an attempt to reduce the coupling of the two phenomena. The strain controlled tests imparted the specimen with symmetric tension compression cycles within the strain range of ±0.75%. Following the strain hardening stabilization process, post-stabilized monotonic, uniaxial and biaxial tests were conducted.

The post-stabilized monotonic tension tests were continued up to 1.8% strain. In uniaxial testing, there are two concepts of conducting tests under stress control. The first concept of uniaxial testing is performing incremental loading and unloading to zero load in order to establish an elastic limit, by reading the total strain, which is recorded at every unloaded zero load. In this test, the stress increment for every subsequent loading is set at 4 MPa. The second concept of uniaxial testing is to establish the uniaxial ratcheting rate. Here, the applied stress range is set to 255 MPa under a constant mean stress of 65 MPa.

In the biaxial tests, the pipes were pressurized using a hydraulic pump. The axial load provided by the Instron machine and internal pressure were coupled through a feedback monitoring system so that the internal pressure would only give rise to pure circumferential stress. Under any magnitude of internal pressure, the system would adjust to maintain zero axial pressure stress. Cyclic axial stress would then be provided by the testing machine to study ratcheting. The uniaxial strain of the test specimen was cycled in a symmetric mode. The axial stress and strain are known as (${\sigma }_x, {\mathsf{Ɛ}}_x$), and the circumferential stress and strain are recognized as (${\sigma }_{\theta }, {\mathsf{Ɛ}}_{\theta }$). The internal pressure is denoted by $IP$ and the strain amplitude of the cycles is identified by ${\mathsf{Ɛ}}_{xc}$. In the biaxial tests, the strain was controlled and cycled and the stress response was logged. The strain limit is ${\mathsf{Ɛ}}_{xc}=\pm 0.4\%$. The internal pressure was set at $IP=5 \mathrm{MPa}$. It is worth mentioning that as with other researches, the loading rate-dependent behavior of the material and pipes was not studied [30,34,35].

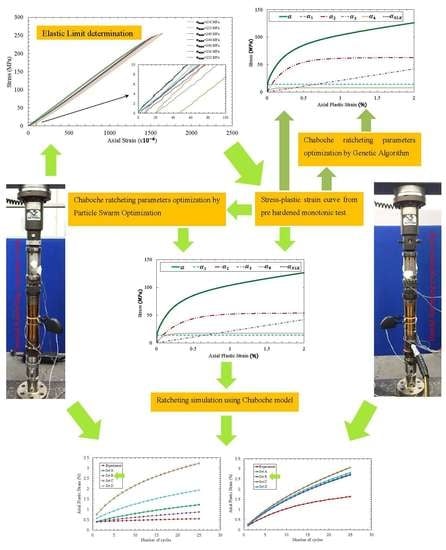
2.4. Experiment Results and Discussion

The result from the stabilized uniaxial strain control test is illustrated in Figure 6a,b. Figure 6a demonstrates the cyclic hardening in the strain-symmetric cyclic history. The hysteresis loop tends to limit itself to a closed stable loop after a number of cycles. The hysteresis loop is stabilized after eleven cycles in which the pipe exhibits significant hardening before stabilization. In the subsequent strain symmetric cycling, the specimens are unloaded to zero magnitude of axial stress and strain. Figure 6b shows the final stabilized hysteresis loop of the test.

The results of the monotonic tensile test and post-stabilized monotonic test are shown in Figure 7. The test was conducted for a strain range of 0 to +1.8% where the stress-strain plot exhibits strain hardening after the elastic limit. The yield points at 0.2% strain offset are calculated to be 264 MPa and 305 MPa for monotonic and post-stabilized monotonic test, respectively. Most of the ratcheting parameters are obtained from the monotonic, post-stabilized monotonic, and stabilized hysteresis curves.

Figure 8 depicts the stress-strain responses from the monotonic and post-stabilized monotonic test superimposed on the upper hysteresis curve result from cyclic test with symmetric strain control in the plastic region. The figure shows the effect of material hardening on the stabilization of stress-strain behaviour after several loading cycles. It can be observed that strain hardening causes a significant increase of the linear section of the post-stabilized monotonic test and the hardening is caused by cyclically stabilized axial strain symmetric cycling, rather than first half tension of strain control monotonic test. In the figure, the transient Bauschinger effect can be observed, which gives rise to a smaller plastic modulus in the stabilized hysteresis loop compared to the post-stabilized monotonic loading. This happens if the applied peak strain is relatively small in prior strain control hardening [36,37,38,39]. The “shifted curve” in Figure 8 refers to the stress and strain data obtained in the upper or lower stabilized hysteresis loading. The shifted curve (${\mathsf{\sigma }}_{\mathrm{shift}},{\mathsf{Ɛ}}_{\mathrm{shift}})$) obtained from upper curve is regularized by the following equations:

$${\mathsf{\sigma }}_{\mathrm{shift}}=\frac{1}{2}({\mathsf{\sigma }}_{\mathrm{Upper} \mathrm{curve}}-{\mathsf{\sigma }}_{\mathrm{Max} \mathrm{at} \mathrm{maximum} \mathrm{strain} \mathrm{control}}),$$

(1)

$$\mathrm{and} {\mathsf{Ɛ}}_{\mathrm{shift}}=\frac{1}{2}({\mathsf{Ɛ}}_{\mathrm{Upper} \mathrm{curve}}-{\mathsf{Ɛ}}_{\mathrm{Max} \mathrm{at} \mathrm{maximum} \mathrm{strain} \mathrm{control}}).$$

(2)

From Figure 8, the knee section of the calculated shifted curve is positioned below the knee sections of monotonic and post-stabilized monotonic curves because the quasi linear segment of shifted curve is shorter in comparison to the monotonic and post-stabilized monotonic curves. Hence, the shifted curve, obtained from hysteresis curve, does not present the true mode of monotonic behaviour of the material.

Figure 9 illustrates the stress-strain response of the uniaxial tests in which the subsequent maximum load is incremented by 4 MPa after every complete unloading. The loading-unloading process is continued when a large permanent axial deformation occurs. From the figure, for the cycle with maximum stress ${\sigma }_{Max}$ of 244 MPa, the strain starts from 0 με at zero load and remains 0 με upon unloading. For the cycle with maximum stress of 248 MPa, the strain starts from 0 με at zero load and retains 7.5 με upon unloading. For the cycle with maximum stress ${\sigma }_{Max}$ of 252 MPa, the strain starts from7.5 με at zero load and reads 20 με upon unloading. The loading cycle before the one that initiates the plastic strain is considered in the calculation for the elastic limit. Many loading cycles were carried out, but since the curves are quite close to one another, only three cycles before and after the elastic limit cycle are depicted. From Figure 9, the elastic limit is found to be 244 MPa, which is 0.8 times of yield stress (305 MPa) at 0.2% strain offset.

Figure 10a shows the stress-strain response obtained from uniaxial stress controlled ratcheting test. The stress was cycled from −190 MPa to 320 MPa, thus giving a mean stress of 65 MPa. The figure shows that at the start of the test, the rate of ratcheting is about 100 με per cycle, which then ceases in 25 cycles. This means that the plastic strain in the axial direction increases by 100 με for every cycle for 25 cycles. In this test, the pipe did not fail due to ratcheting, but had the test been continued, it would have failed by other modes. The maximum strain recorded in each cycle is plotted as a function of the number of cycles and the result is presented in Figure 10b.

The biaxial ratcheting test result of the axial strain ${\mathsf{Ɛ}}_x$ and hoop strain ${\mathsf{Ɛ}}_{\theta }$ response is shown in Figure 11a. In this strain controlled test, the axial strain was cycled from −4000 με to +4000 με. Ratcheting in ${\mathsf{Ɛ}}_{\theta }$ can be observed. For the first 14 cycles, the ratcheting rate is higher, but after this the rate becomes lower and constant. Figure 11b shows the plot of the circumferential plastic strain recorded in each cycle as a function of the number of cycles applied. The figure shows that ratcheting in the hoop direction does not cease, but continues at a constant rate of 500 με per cycle. Theoretically, in this case, ratcheting will be the mode of failure, but the test was interrupted after 25 cycles.

3. Automated Calibration of Chaboche Parameter

The aim of the calibration procedure is to define the optimized input Chaboche model parameters for elastic-plastic analysis by means of the Chaboche model. The Chaboche parameters can be identified and calibrated based on a stress-plastic strain monotonic curve, as shown in Figure 7. The parameters can also be calibrated by using the stabilized stress-plastic strain hysteresis curve from a uniaxial strain control test, as illustrated in Figure 6b. The experimental uniaxial ratcheting is shown in Figure 10b. After identifying and employing the parameters, they would be adopted for any cyclic loading and geometry, on condition that the same stress range is nominated as shown in Figure 6 and Figure 7.

3.1. Chaboche Model of Ratcheting

The rate-independent form of the non-linear kinematic hardening model (NKH) recommended by Chaboche [11,40] is employed here. The model primarily consists of superposition of several (3, 4 or 5) Armstrong Frederick (A–F) kinematic hardening (KH) rules. The kinematic hardening (KH) rule encompasses a ‘recall term’, which embeds the fading memory effect of the strain path. The constitutive equation is established on a von-Mises yield criterion, linear isotropic elasticity and the associated flow rule. The proposed equation for the backstress, dα, proposed by Armstrong—Frederick is given by [11]:

$$d\alpha =\frac{2}{3}Cd{\mathsf{Ɛ}}^p-\gamma \alpha dp,$$

(3)

$$\mathrm{where} dp=\left|d{\mathsf{Ɛ}}^p\right|={\left[\frac{2}{3}d{\mathsf{Ɛ}}^p·d{\mathsf{Ɛ}}^p\right]}^{1/2}$$

(4)

Chaboche et al. [40] proposed a ‘decomposed’ nonlinear kinematic hardening rule in the form:

$$d\alpha ={\displaystyle \sum }_{i=1}^{M}d{\alpha }_i,d{\alpha }_{i }=\frac{2}{3}{C}_{i }d{\mathsf{Ɛ}}^p-{\gamma }_{i }{\alpha }_{i }dp,$$

$$\mathrm{where} dp=\left|d{\mathsf{Ɛ}}^p\right|.$$

Both $C_i$ and ${\gamma }_{i }$ are constants in the Chaboche kinematic hardening model, which can be generated from the monotonic and uniaxial strain controlled stable hysteresis loop. As shown in Equation (5), the Chaboche model is an incorporation of several (A–F) hardening rules. Particular objectives are represented by each of these decomposed rules. For example, if M = 4, the first kinematic hardening rule ${\alpha }_1$ predominantly signifies the first loop section by initiating with a quite large slope and following by quick stabilization. The fourth loop section is nearly linear along with a slight slope and is denoted by the third rule ${\alpha }_3$. The transition knee part of the hysteresis curve is partitioned into two sections. The second section is represented principally by the fourth hardening rule ${\alpha }_4$ and third section by the second hardening rule ${\alpha }_2$. Hence, the initial slope of the first segment is a good estimation for C1, the third segment for C2, the fourth segment for C3, and the second segment for C4. The details on the physical description and calculation procedure of the Chaboche parameters are discussed in [11,26].

The von-Mises yield criterion is represented as:

$$f\left(\sigma -\alpha \right)={\left[\frac{2}{3}\left(s-\mathrm{a}\right)·\left(s-\mathrm{a}\right)\right]}^{1/2}={ б}_0,$$

(6)

and the supplementary flow rule can be described by the following expression:

$$d{\mathsf{Ɛ}}^p=\frac{1}{H}\left\{\frac{\partial f}{\partial \sigma }·d\sigma \right\}\frac{\partial f}{\partial \sigma },$$

(7)

where, $\sigma$ is the stress tensor, $\mathrm{s}$ is the deviatoric stress tensor, $\mathsf{\alpha }$ is the current center of the yield surface, $\mathrm{a}$ s the current centre of the yield surface in deviatoric space, ${б}_0$ is the size of the yield surface and is constant for a cyclically stable material, which defines the initial yield strength at the defined elastic limit of the material in an uniaxial tension test. $H$ is the plastic modulus and in the above formulation, $\left\{\mathbf{0}\right\}$ indicates the MacCauley bracket and the inner product is expressed by a $·$ b = aijbij.

Therefore, for a one-dimensional representation of an NLK model, the $\mathsf{\alpha }$ backstress is achieved from Equation (8).

$$\alpha ={\sigma }^1-{\sigma }_0^1,$$

(8)

where, ${\sigma }^1$ is the uniaxial stress of a tension specimen and ${\sigma }_0^1$ is the elastic limit stress. Referring to Chaboche model with M components, the ${\alpha }_{NLK}$ backstress is described by Equation (9).

$${\alpha }_{NLK}={\displaystyle \sum }_{i=1}^M{\alpha }_{i },$$

(9)

where, ${\alpha }_{i }$ can be calculated from the monotonic test and upper hysteresis curves by Equations (10) and (11), respectively.

$${\alpha }_i=\left(\frac{C_{i }}{{\gamma }_{i }}\right)\left[1-\exp \left(-{\gamma }_{i }{\mathsf{Ɛ}}_{p }\right)\right],$$

(10)

$${\alpha }_i=\left(\frac{C_{i }}{{\gamma }_{i }}\right)\left[1-2\exp \left(-{\gamma }_{i }({\mathsf{Ɛ}}_p+{\mathsf{Ɛ}}_{p0})\right)\right].$$

(11)

In the positive half cycle of the hysteresis curve, ${\mathsf{Ɛ}}_{p0}$ is called the starting point, where plastic strain is zero and ${\mathsf{Ɛ}}_{p }$ is the plastic strain from stress-plastic strain experiment data. The plastic strain range for the segments is determined through extensive trial-and-error runs of the modified Chaboche model program [22,25].

The validity of the M numbers of parameters depends on the requisite that the ${\alpha }_{NLK}$ backstress curve accurately overlaps α backstress curve. The selection of the appropriate number of components, M, might be an iterative process and is based on the eye of the analyst and error function of intelligent optimization technics. For example, if M = 2 does not meet the required match of the backstress curves, then M = 3 and 4 etc. must be tried. Furthermore, the value at the saturation point of each component, addressed by ${\alpha }_{\begin{array}{c}Si\\ \end{array}}$, at which the ith component has zero slope is assumed by Equation (12).

$${\alpha }_{si}=\left(\frac{C_{i }}{{\gamma }_{i }}\right),$$

(12)

at the point where the ${\alpha }_{NLK}$ backstress curve is saturated to zero slope, the ratcheting parameters, $C_i$ and ${\gamma }_{i }$, give the value ${\alpha }_S$ of Equation (13):

$${\alpha }_S={\displaystyle \sum }_{i=1}^M\frac{C_{i }}{{\gamma }_{i }}$$

(13)

3.2. Extraction of Stress-Plastic Strain Data

The extracted stress-plastic strain curve provides the main result that is used to calibrate the ratcheting parameters. The elastic limit in Figure 6b and Figure 7, must initially be defined and determined. Since ratcheting is a measure of accumulated strain, the stress at the elastic limit of the material becomes the starting point of analysis. The method of using offset strain to define elastic limit in monotonic test is done by finding the intersection on the stress-strain curve with a line parallel to the initial stress-strain slope running through the offset strain. Using the elastic limit, the stress-plastic strain curve for monotonic and upper stabilized hysteresis curves are calculated by Equations (14) and (15), respectively:

$${\mathsf{Ɛ}}_P={\mathsf{Ɛ}}_T-\left(\left(\frac{\sigma }{E}\right)+{\mathsf{Ɛ}}_{off}\right),$$

(14)

$$\mathrm{where} {\mathsf{Ɛ}}_{off}={\mathsf{Ɛ}}_{TEl}-\frac{{\sigma }_{El}}{E}$$

$${\mathsf{Ɛ}}_P={\mathsf{Ɛ}}_T+\left(\left(\frac{{\mathsf{Ɛ}}_0+2\ast {\sigma }_{El}-\sigma }{E}\right)\right),$$

(15)

where, ${\mathsf{Ɛ}}_P$ is plastic strain,${\mathsf{Ɛ}}_T$ is total strain, $\sigma$ is stress, E is Young’s modulus, ${\mathsf{Ɛ}}_{off}$ is elastic strain offset, ${\mathsf{Ɛ}}_{TEl}$ is total strain at elastic limit, ${\sigma }_{El}$ is elastic limit stress and ${\mathsf{Ɛ}}_0$ is the start of half cycle strain.

The elastic limit for stainless steel was assumed by Kalnins et al. [22] as 0.55 times the yield stress which was determined using a plastic strain offset ${\mathsf{Ɛ}}_{off}$ of 0.2%, as depicted in Figure 7. The basis of the factor of 0.55 comes from its use in the calibration of the Chaboche material models by AREVA GmbH Erlangen [22] as mentioned before. Multiplying the 0.2% proof stress of 305 MPa (in Figure 7) by the factor 0.55 gives the elastic limit of 167.2 MPa for post-stabilized monotonic and upper hysteresis curve shown in Figure 12.

The factor of 0.55 is quite conservative, as discussed in Section 1. From Figure 9, using the proposed incremental uniaxial method on post-stabilized monotonic curve, the elastic limit for 316L stainless steel was measured as 244 MPa. This value of elastic limit is 0.80 times the yield stress as discussed in Section 2.4. Using the elastic limit of 244 MPa (from incremental method proposed by current study) and 167.2 MPa (from Kalnin’s [22] method), the stress-plastic strain data is obtained and presented in Figure 12 and Figure 13, respectively. Hence, the plastic strain range of the hysteresis curve has been enlarged to 2% and the slope of the upper hysteresis stress-strain curve extends the monotonic curve beyond 0.75% strain. This is because the plastic strain range of the hysteresis curve is supposed to be as large as all kinematic hardening rules curves saturated within the dedicated plastic strain range [25]. The backstress α is calculated using Equation (8) and included in Figure 12 and Figure 13.

3.3. Parameter Generation Based on Physical Meaning

In this subsection, a curve fitting process is adopted. The number of components that are needed for evaluation of the accuracy of the ${\alpha }_{NLK}$ backstress curve are set as M = 4 [25]. The stress-plastic strain data obtained from Section 3.2, together with their corresponding Backstress α obtained from Equation (8), are presented in Figure 12 and Figure 13. Through trial and error, Rahman [25] first, roughly estimate the contribution of a set of three ratcheting parameters, $\frac{C_1}{{\mathsf{\gamma }}_1}$, $\frac{C_2}{{\mathsf{\gamma }}_2}$ and $\frac{C_4}{{\mathsf{\gamma }}_4}$, to be used as hysteresis curve of several stainless steels and carbon steels by the following equation:

$$2\ast \left(\frac{C_1}{{\mathsf{\gamma }}_1}\right)+2\ast \left(\frac{C_2}{{\mathsf{\gamma }}_2}\right)+2\ast \left(\frac{C_4}{{\mathsf{\gamma }}_4}\right)={\sigma }_x^{+}-{\sigma }_x^{-}-2\ast {\sigma }_0-2\ast C_3{\mathsf{Ɛ}}_L^p$$

(16)

where, ${\sigma }_x^{+}$ is the positive peak, ${\sigma }_x^{-}$ is the negative peak of the hysteresis curve and ${\mathsf{Ɛ}}_L^p$ is plastic strain range. Therefore, the right hand side of Equation 16 can be determined. The first rough contribution can be estimated then for $2\ast \left(\frac{C_1}{{\mathsf{\gamma }}_1}\right)$, $2\ast \left(\frac{C_2}{{\mathsf{\gamma }}_2}\right)$ and $2\ast \left(\frac{C_4}{{\mathsf{\gamma }}_4}\right)$. In the current study, this method is adopted for the post-stabilized monotonic curve by dividing both sides of Equation (16) by two. Hence in the first step, the initial estimates of Cs and γs are allowed to evolve or adapt with generation, which is found to improve the convergence speed. In the second step, Equation (17) is adopted for all plastic strain data proportional to Backstress ${\alpha }_{NLK}$, but ${\mathsf{\gamma }}_3$ is considered zero.

$${\alpha }_{NLK}={\alpha }_1+{\alpha }_2+{\alpha }_4+\left(C_3\ast {\mathsf{Ɛ}}_{p }\right).$$

(17)

The range used for each parameter for random generation of population, using PSO and GA intelligent methods, are as follows: ±5% for $C_1$ and $C_3$ because these parameters can be estimated more accurately than others. The parameters $C_2$, $C_4$, ${\mathsf{\gamma }}_1$, ${\mathsf{\gamma }}_2$, and ${\mathsf{\gamma }}_4$ are varied ±10% of the initial estimate. Therefore, the Chaboche stress ${\sigma }_{NLK}$ is acquired by Equation (18):

$${\sigma }_{NLK}={\alpha }_{NLK}+{\sigma }_0^1.$$

(18)

Finally the value of ${\mathsf{\gamma }}_3$ is calibrated when other parameters are kept constant. Calibration is carried out within the range of 0–10 in uniaxial simulation, as described in Section 4.

3.4. Determination of Ratcheting Parameters Using Intelligent Optimization Methods

Intelligent optimization is used to determine the ratcheting parameters to ensure the least deviation between simulation results and ratcheting tests. Two intelligent methods, namely Genetic Algorithm (GA) and Swarm Particle Optimization (PSO) are discussed in this study. The Chaboche parameters are the independent parameters in the cost function equations, which are calculated by intelligent algorithms assigned in GA and PSO structures. In this study the GA is programmed for one main function, while algebraic calculations for selection, double crossover and mutation are considered as separate functions during the running of program. On the other hand, PSO possesses less programming than GA by utilizing one main function in which all algebraic calculation for velocity and position of members (Chaboche parameters) are programmed. The accuracy of both methods depends on similarity matching between $\alpha$ and ${\alpha }_{NLK}$ backstress curves as described in Section 3.1. The procedures for both GA and PSO methods are presented.

3.4.1. Genetic Algorithm

Genetic Algorithm is a versatile optimization method in which the best solution is found by assigning a big population of individuals to satisfy cost functions such as minimizing cost function or maximizing fitness function. Artificial GA mimics the evolution of living in nature encompassing selection, cross over, and mutation.

The Genetic Algorithm is commonly adopted as a method to identify parameters of physical models to satisfy the cost function [25,26,41]. Herein, the cost function is the Chaboche stress ${\sigma }_{NLK}$ which is the function of backstress mentioned in Section 3, and expressed as Equation (19):

$${\sigma }_{NLK}= f\left({\alpha }_{NLK}\right),$$

(19)

$$\mathrm{where} {\alpha }_{NLK}=f\left(C_1,C_2,C_3,C_4,{\mathsf{\gamma }}_1,{\mathsf{\gamma }}_2,{\mathsf{\gamma }}_4, {\sigma }_0^1\right).$$

Therefore ${\sigma }_{NLK}$ is a dependant variable and $x_{GA}=\left\{C_1,C_2,C_3,C_4,{\mathsf{\gamma }}_1,{\mathsf{\gamma }}_2,{\mathsf{\gamma }}_4\right\}$ is an independent variable, known as chromosome. The parameter optimization and model can be evaluated by calculating the mean square error (MSE) as presented in Equation (20):

$$MSE=\frac{1}{N}{\displaystyle \sum }_{i=1}^N{({\sigma }^1-{\sigma }_{NLK})}^2,$$

(20)

where, N is the number of proportional strain data points from the experiment. To perform the GA, the three main steps, namely, selection, crossover and mutation are to be implemented.

Selection Activity

Selection is the repetitive action of forming an initial population, which adapts into a new superior population. In this study the initial population is made randomly by choosing a real number. To proceed selecting a new population, the roulette wheel method is used to select chromosomes. Each chromosome possesses its own probability ($P_i$), defined as:

$$P_i=\frac{{\mathrm{Ć}}_{max}-{\mathrm{Ć}}_i}{{{\displaystyle \sum }}_{j=1}^{npop}({\mathrm{Ć}}_{max}-{\mathrm{Ć}}_{j)}}$$

(21)

where, $npop$ is the number of chromosome in population, ${\mathrm{Ć}}_{max}$ is maximum cost function, ${\mathrm{Ć}}_i$ is current chromosome cost function and ${\mathrm{Ć}}_j$ is cost function of remaining chromosomes. After characterizing the eligibility of each chromosome, the roulette wheel tries to select members according to the high probability criterion. The cumulative vector is the sum of probabilities:

$$v=\left[p_{1 ,} p_{1+ }{p}_{2 ,}{p}_{1+ }{p}_{2+}{p}_{3 ,\dots ,}{p}_{1+\dots +}{p}_n\right]$$

(22)

or in the new form:

$$v\left(i\right)={\displaystyle \sum }_{j=1}^i{p}_{j },$$

(23)

$$\mathrm{where} i=min\left\{j|r\le v_j\right\} 0<r<1,$$

where $i$ is an index of iteration to promote chromosomes of old population to build the new eligible population. Selection is a fundamental task that should be done before and after crossover and mutation activities.

Crossover Activity

The main purpose of crossover is to produce a new population member (chromosome) that shares the partial characteristics of parents. The manifestation of two new offsprings is a result of combining two mature parent chromosomes. If $x_1$ and $x_2$ are considered as parents, then ${\widehat{x}}_1$ and ${\widehat{x}}_2$ may be introduced as offsprings. As mentioned before, each chromosome contains Chaboche parameters; thus, the crossover can be presented as:

$$x_1=\left(C_{11} ,{ \mathsf{\gamma }}_{11} ,C_{12} ,{ \mathsf{\gamma }}_{12} ,C_{13} ,C_{14} ,{\mathsf{\gamma }}_{14}\right),$$

(24)

$$x_2=\left(C_{21} ,{ \mathsf{\gamma }}_{21} ,C_{22} ,{ \mathsf{\gamma }}_{22} ,C_{23} ,C_{24} ,{\mathsf{\gamma }}_{24}\right),$$

(25)

And

$${\widehat{x}}_{1i}={\dot{\alpha }}_i{x}_{1i}+\left(1-{\dot{\alpha }}_i\right)x_{2i},$$

(26)

$${\widehat{x}}_{2i}={\dot{\alpha }}_i{x}_{2i}+\left(1-{\dot{\alpha }}_i\right)x_{1i},$$

(27)

where, ${\dot{\alpha }}_iϵ\left\{0,1\right\}$ is the result of the crossover and can be indicated below, considering ${\dot{\alpha }}_i=\frac{1}{2}$ and $i=1;$

$${\widehat{x}}_{11}=\frac{1}{2}{c}_{11}+\left(1-\frac{1}{2}\right)c_{21},$$

(28)

$${\widehat{x}}_{21}=\frac{1}{2}{c}_{21}+\left(1-\frac{1}{2}\right)c_{11},$$

(29)

the new chromosomes ${\widehat{x}}_1$ and ${\widehat{x}}_2$ are created to minimize MSE in Equation (20).

Mutation Activity

The occurrence of mutation phenomenon in nature is to create new population members with best adaptivity towards the surrounding environment. However, in an artificial environment, mutation is designed to satisfy the cost function without any crossover activity. In other words, one parent mutates into superior version. In our artificial programming, the mutation is implemented to change one part of the chromosome $\widehat{x}$ in the form of:

$$\widehat{x}\left(i\right)=x\left(i\right)+\gamma \ast \beta ,$$

(30)

where, $\gamma$ is weighted value that is produced by:

$$\gamma =0.1\ast \left(varmax-varmin\right).$$

(31)

In Equation (31),$varmax$ and $varmin$ are the maximum and minimum values of the variable that each chromosome can possess, respectively. $\beta$ is a nominal value selected randomly to allot to size (length) of each chromosome. In Equation (30), the $i$th element of chromosome is replaced by a new value. Finally, the capable population is chosen after crossover and mutation to build a new population in which the best chromosomes are selected that minimize MSE in Equation (20).

3.4.2. Particle Swarm Optimization

To extract the optimum Chaboche parameters, GA was first introduced in which the MSE of $\alpha$ and ${\alpha }_{NLK}$ reach minimum values. The PSO method is implemented in a comparative way to GA in minimizing MSE. In PSO, the population members interact directly among themselves.

PSO Formulation

Particle Swarm Optimization (PSO) is another artificial intelligent method employed to mimic the social natural movement of some animal species such as fishes and birds. In contrast to GA, the optimization process in PSO is done by direct intelligent interaction among the population members. In each iteration, the current cost function (MSE) of members (particles) are evaluated and compared with its previous (local) and global values to create a new eligible population. In this method, the position and speed of each particle in each iteration are evaluated for a new particle position that minimizes the cost function. The members are selected or ranked based on best fitness value as indicated by minimized MSE [42]. This team working activity is mathematically explained in an equation, which presents the new position of the member as:

$$x_i^{new}=x_i^{old}+v_i^{new},$$

(32)

where, $x_i^{new}$ is the optimum solution for a member in the population, in our case the $x_i^{new}$ is the latest Chaboche parameter that is minimized in MSE. $x_i^{old}$ is the previous position and $v_i^{new}$ is the velocity (direction) of member that can be described as:

$$v_i^{new}=t_1{r}_1\left(x_i^{local}-x_i^{old}\right)+t_2{r}_2\left(x^{global}-x_i^{old}\right)$$

(33)

where, $v_i$ is the velocity of the particle,$w$ is the inertial coefficient and $r_{1 }$ is a random number between 0 and 1. It is set $t_1+t_2=4$.

Equation (33) is schematically presented in Figure 14 in which the new position is the best position of the member satisfying the cost function (MSE). The best member has the optimum Chaboche parameters in Equation (33).

The overall GA and PSO optimization process flowcharts are illustrated in Figure 15a,b, respectively, with their elements (cost function, constraints, etc.) described in detail in the following.

3.5. Results and Discussions—Automated Parameter Calibration of Chaboche Model

The stress-plastic strain parameters determined using the PSO and GA schemes are calculated after setting 244 MPa as the elastic limit, which was obtained from incremental uniaxial test result in Figure 9 and listed in

Table 3. PSO and GA calibration for post-stabilized monotonic curve with elastic limit 244 MPa.

Type	PSO Method	GA Method
$C_{1-4}$	296870, 17958, 2118, 20508	300871, 25155, 2118, 14182
${\gamma }_{1-4}$	21179, 335, 0, 1196	21803, 402, 0, 1903
Optimization Time (s)	617	721
MSE	0.325	0.691

. The $\alpha$ and ${\alpha }_{NLK}$ curves are obtained from Equations (3) and (5) and presented in Figure 16. ${\mathsf{\gamma }}_3$ is considered to be zero.

In contrast to GA, the particles in the PSO method have less mathematical operations. Thus, only a few parameters are left to be adjusted and this saves time compared to GA. After evaluation in every iteration, the cost function of each particle is compared with past, local and global values to select the most eligible particle as upcoming member. Each member iteratively gets its new position and velocity to be evaluated in order to minimize the cost function. In this study, both methods are compared for accuracy in satisfying the cost function. Since the PSO method had resulted in more accurate parameters (in terms of MSE) and less optimization time, the PSO scheme was adopted in generating the ratcheting parameters for the stress–plastic strain results in Figure 12 and Figure 13.

The ratcheting parameters for post-stabilized monotonic and hysteresis loadings, with different elastic limit adoptions, 167.2 MPa and 244 MPa, calculated using the PSO method are presented in

Table 4. PSO method—Calibration for Set A, Set B, Set C and Set D.

Type	Set A	Set B	Set C	Set D
$C_{1-4}$	2446600, 12207, 2118, 24246	296870, 17958, 2118, 20508	140520, 29589, 2118, 31040	140220, 16725, 2118, 15818
${\gamma }_{1-4}$	27439, 291, 0, 796	21179, 335, 0, 1196	4471, 899, 0, 325	47864, 282, 0, 732

. For simplicity, the set of parameters obtained from post-stabilized monotonic stress-plastic strain curve with adopted elastic limits 167.2 MPa and 244 MPa are named Set A and Set B, respectively. Parameters obtained from hysteresis stress-plastic strain with adopted elastic limits of 167.2 MPa and 244 MPa are named Set C and Set D, respectively, and shown in Table 4.

4. Finite Element Model

The finite element (FE) pipe models with boundary conditions are shown in Figure 17 and Figure 18, in which ¼ of the structure is modeled and meshed with ANSYS Solid186 elements, as shown in Figure 17 and Figure 18. The models are symmetric about the pipe mid-span (X -Y plane) and about the plane of bending (Y -Z plane). The stress and strain data are extracted from elements at the pipe mid-span; hence, the elements in this section were sized smaller than those in the remainder of the pipe. A mesh convergence test was performed and analyses of 10 FE meshes of the pipe model were carried out for 20 cycles of the biaxial loading, as carried out in the experiment. The Chaboche plasticity model for both mesh convergence and simulation studies are readily available in ANSYS. This model is then used with ratcheting parameters obtained in Section 3.5. An elastic-plastic uniaxial FEA simulation was performed to calibrate the ${\mathsf{\gamma }}_3$ while the other parameters that were determined in Section 3.5 were kept constant. After calibrating ${\mathsf{\gamma }}_3$, biaxial ratcheting was performed using the calibrated ratcheting parameters.

5. Finite Element Results and Discussion

Figure 19 shows the Chaboche model simulation results for the uniaxial and biaxial loadings, using ratcheting parameters presented in Table 4. The value of ${\gamma }_3\left(=3\right)$ had been calibrated using uniaxial loading simulation. For different ratcheting parameter sets, the results are evaluated in terms of two main concepts. The first evaluation concept involves simulation results obtained from Sets A and B. The second concept involves simulation results obtained from Sets C and D.

When the parameters in the model are determined using uniaxial loading tests, the numerical simulation results show closer correlation to the uniaxial test rather than the biaxial test, but all simulation results overpredict test results. The uniaxial and biaxial ratcheting simulation results using Sets A and B are closer to test results in comparison to those obtained from Sets C and D. The good correlation is due to reduction in transient Bauschinger effect, because the yield point of the shifted curve is positioned lower than the monotonic and post-stabilized monotonic curves, as shown in Figure 8 and discussed in Section 2.4. The ratcheting parameters obtained from the hysteresis curve present the same trend with the shifted curve in FE simulation for monotonic section. The curve accordance or matching between ($\sigma , \mathsf{Ɛ}$) from the post-stabilized monotonic test with $({\sigma }_{shift}$,${\mathsf{Ɛ}}_{shift}$) from shifted curve depends on material and strain amplitude of pre-hardening strain control test and this match occurs only for one value of strain range for every different material. Finding this matching requires many trial-and-error tests. Even so, this match is suitable only for limited ratcheting tests that are within the same strain range of the matched hysteresis curve. Hence, the hysteresis curve is not suitable to be used in generating Chaboche ratcheting parameters compared to post-stabilized monotonic curve.

Adopting an accurate elastic limit in Sets B and D gives a more precise yield stress surface, compared to Sets A and C, respectively. The ratcheting rate predicted in uniaxial loading is quite close to experimental results with parameters obtained from Set B, with slight overestimation but with similar trend of the curve.

6. Conclusions

In this paper, Chaboche ratcheting model parameters for 316L stainless steel pipes were determined from experimental uniaxial and hysteresis loading. The parameters were optimized using two different multi objective intelligent optimization technics, namely, Particle Swarm Optimization (PSO) and Genetic Algorithm (GA) methods. Experiments were conducted in which all test specimens were cyclically stabilized in a symmetric ±0.75% strain control loading prior to the following tests-monotonic uniaxial test, incremental uniaxial test, uniaxial and biaxial ratcheting tests.

The elastic limit, obtained from incremental uniaxial test, plays an important role in the accuracy of prediction of ratcheting rate. Two methods were adopted from which the elastic limit was extracted; the first from experimental stress-plastic strain hysteresis curve and the second from post-stabilized monotonic curve. The stress-plastic strain curve is also employed to find ratcheting parameters. Parameter ${\mathsf{\gamma }}_3$ is obtained using PSO and GA methods. A uniaxial ratcheting test was conducted to calibrate ${\mathsf{\gamma }}_3$ with uniaxial ratcheting rate simulation. The uniaxial and biaxial ratcheting simulations were validated with experiments. Based on the analysed data, the main results can be summarized as follows:

• Tests on 316L austenitic steels show the presence of transient Bauschinger effect in upper hysteresis curve with of ±0.75% symmetric strain hardening range in comparison with post-stabilized monotonic curve.
• The efficiency of generating ratcheting parameters, in terms of MSE and optimization time, is better in the PSO method compared to GA.
• The elastic limit obtained from the incremental uniaxial test after pre-hardening offers an improved uniaxial ratcheting prediction.
• Compared to the hysteresis curve, the ratcheting parameters obtained from post-stabilized monotonic curve present more accurate ratcheting prediction.

Most of the material parameters for ratcheting prediction models implemented in FEM software such as ANSYS and ABAQUS, are determined from the uniaxial hysteresis test curve. The current study presents parameter determination and calibration for subsequent implementation of Chaboche ratcheting model in ABAQUS and ANSYS. The current material parameters can be adopted for other ratcheting models such as Modified Chaboche, Ohno-Wang, Armstrong-Frederick-Ohno-Wang and Chen-Jiao-Kim (CJK). Since most of these models parameters are supposed to be obtained from hysteresis test curves, the present results can be compared with other ratcheting models predictions.