Functional Data Analysis in Sport Science: Example of Swimmers’ Progression Curves Clustering

Abstract

Many data collected in sport science come from time dependent phenomenon. This article focuses on Functional Data Analysis (FDA), which study longitudinal data by modelling them as continuous functions. After a brief review of several FDA methods, some useful practical tools such as Functional Principal Component Analysis (FPCA) or functional clustering algorithms are presented and compared on simulated data. Finally, the problem of the detection of promising young swimmers is addressed through a curve clustering procedure on a real data set of performance progression curves. This study reveals that the fastest improvement of young swimmers generally appears before 16 years old. Moreover, several patterns of improvement are identified and the functional clustering procedure provides a useful detection tool.

1. Introduction

1.1. Longitudinal Data in Sport

For a long time, sport science has been interested by time dependent phenomenons. If, at first, people only kept track of performance records, there is currently a massive amount of various data. Among them, one specific type is called time series or longitudinal data. Many recorded and studied data can be considered as time series depending on the context. From the heart rate during a sprint [1], to the number of injuries in a team over a season [2], to the evolution of performances during a whole career [3], the common ground remains the evolution of a characteristic regarding a time period. An interesting property of such data lies in the dependency between two observations at two different instants, leading, in mathematical terms, to the fact that the independent and identically distributed (iid) hypotheses are not verified. However, most of the usual statistical tools classically used in Sport Science, such as the law of large number and central limit theorem, need these properties (Note that there exist several versions of these theorems with more or less flexible hypotheses, depending on the context. We talk here about the most common versions, classically used in applied science). Thus, all the statistical methods based on these results (hypothesis testing, method of moments and so on) collapse, and one needs specific tools to study time series. There is a whole literature related to the subject [4]. These methods focus on the study of time dependent processes that generate discrete observations. For instance, since an important topic of this paper concerns clustering, and a really comprehensive review about clustering of time series can be found in [5].

Despite the usefulness of the time series approach, some theoreticians proposed a new modelling of longitudinal data [6]. In many cases, the studied phenomenon is actually changing continuously over the time. Thus, the object we want to know about is more of a function than a series of points. In their paper [2], the authors highlight that it may be damageable to discretize phenomenons that are intrinsically functional. Moreover, they claim that continuous methods perform better than discrete ones on the specific case of the relationship between training load and injury in sport.

In some particular cases, it thus seems natural to model a continuous phenomenon as a random function of time, formally a stochastic process, and consider our observations as just a few records of an infinite dimensional object. This approach is called functional data analysis (FDA) and gives a new range of methods well suited to work on longitudinal data. There was substantial theoretical improvements in the area the last two decades, and this paper intends to present some topics that might be useful to the sport science field. To our knowledge, there are very few papers in the sport literature that use FDA. We can cite [7] in which curve clustering is used to analyse the foot-strike of runners, or [8] for the study of muscle fatigue through a whole FDA analysis. Another example is given in [9] that proposes a functional version of ANOVA using splines to overcome common issues that occur in sport medicine. Finally, the work presented in [10] uses curve clustering methods to study different types of footfall in running. The methodology used in this paper is closely related to our present article, and authors claim that this approach clearly improved analysis of footfall compared to former empirical and observational ways to classify runners.

If such an approach remains marginally applied in the sport field, one would find many examples in a wide range of other domains. We can cite, for example, meteorology, with the article [11] that describes the study of temperature among Canadian weather stations, which has become a classic data set over the years. Another famous data set is presented in [12] as an application to biology, by studying the growth of children as a time continuous phenomenon. Those works and data sets are today considered as benchmarks to test new methods, but many fields such as economy [13], energy [14], medicine [15] or astronomy [16] have used FDA and contribute to this really active research topic.

1.2. Detection of Young Athletes

In the elite sport context, a classical problem lies in the detection of promising young athletes [17]. With professionalisation and evolution of training methods, differences in competition have become more and more tight in recent years [18]. In addition, it has been shown that the development of some specific abilities during adolescence is a key component of improvement [19]. Hence, many sport federations or structures have paid interest in the subject and tried to understand mechanisms behind what could be called talent [20], and the evolution during young years of a career. A key feature to take into account is morphology, since it obviously influences performance in many sports [21]. Morphology is also known as a major noise factor in the detection issue, as the differences in physical maturity leads to promoting some young athletes over others [22] just because of their advantages in height or weight, which will disappear when becoming adults. Some problems raise when these maturity rhythms are ignored, such as in training centres, with an over-representation of athletes born during the first months of the year [23]. Moreover, it appeared in several studies that performance at young ages provides in itself a poor predictor of the future competition results [3]. Only a small portion of elite athletes before 16 years old remains at a top level of performance later [24]. It thus seems clear that the classical strategy, which consists of training intensively in specific structures only best performers of a young age range, reaches its limits. If there are numerous elements that influence performance [25], several works [26] seem to indicate that the evolution over the time of a young athlete is more suited to predict future abilities than raw values at given ages. Different patterns of progression exist, and it might be important to take them into account if one wants to improve quality of talent detection strategies. Our work in this context aims to provide a more global vision of the progression phenomenon by saving its genuine continuous nature. Therefore, model data as functions and study them as such in the frame of FDA might offer a new perspective and provide insights to sport structures for their future decisions.

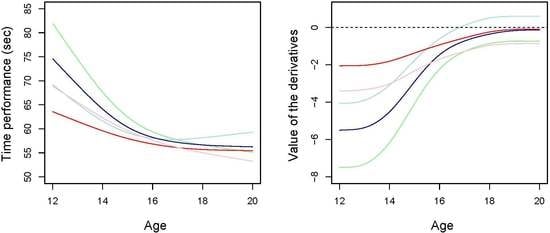
1.3. Functional Data Analysis (FDA)

As mentioned previously, FDA allows for taking into account the intrinsic nature of functional data. Apart from this philosophical advantage in terms of modelling, one may note important benefits. For example, if one records several time series with observations at different instants and/or in different numbers, how can they be compared? How can the evolution of performances of swimmers from their competition times at given ages be studied? Competitors may have different numbers of races during their careers, and their performances are done at different ages (if one wants to avoid age discretization that have been shown problematic in [23]). This example illustrates exactly what we try to deal with in the subsequent curve clustering example. Another fundamental advantage of FDA is the possibility to work on the derivatives of the observed functions. Indeed, it is often interesting to study the dynamic of a time dependent process. Even the second derivative, often referred as the acceleration, or a superior order derivative might provide valuable information in practice. The specific nature of functional data allows for studying such properties, and the sport scientist may easily imagine the wide range of situations on which the study of derivatives might be interesting. One could think for example of the GPS position tracking analysis, the progression phenomenon of young athletes, or the following of the actions of some muscles over time.

The first and fundamental step of a functional data analysis generally consists in the reconstruction of the function from the discrete set of observations. There are two cases at this step. Whether the observations are being considered as error-less (in term of measurement) and one can proceed to a direct interpolation through one of the multiple existing methods (linear, polynomial, ...), or, more frequently, the set $x_{i,t_1},\dots ,x_{i,t_n}$ is considered as observations at time $t_1,\dots ,t_n$ of a realisation $x_i(t)$ of a stochastic process $X(t)$. In this case, one can proceed to a smoothing step. It consists of the approximation of a function defined to be close to the observed points. To deal with noisy data, one always has to face the over-fitting/under-fitting issue. In most cases, one has to determine a smoothing parameter that defines how much one wants to allow the function to contain peaks. These topics are largely detailed in the first chapters of [27]. Even if defining a consistent value of the smoothing parameter is a first work, one can see as an advantage the fact to explicitly control the signal-to-noise ratio of the data. The most common way to reconstruct the function from the observations is to use a basis of functions. A basis of functions is a set of specific functions ${\varphi }_i$ of a functional space $\mathcal{S}$, such as each element of $\mathcal{S}$ being able to be defined as a linear combination of the ${\varphi }_i$. Formally, we can define the basis expansion f as:

$$f(t)=\sum _{i=1}^N{\alpha }_i{\varphi }_i(t),$$

(1)

where ${\varphi }_1,\dots ,{\varphi }_N$ are the basis functions of a given functional space and ${\alpha }_1,\dots ,{\alpha }_N$ are real valued coefficients. Intuitively, if one fixes a common basis to fit observations, the information on individuals is contained in the vector of coefficients $\{{\alpha }_1,\dots ,{\alpha }_N\}$. This is why a common approach is to perform classical multivariate methods on these coefficients. Among the most common bases used in practice, we can cite Fourier basis and wavelets, which are well suited to model periodic data [27,28]. Fourier basis is a widespread choice that works well when data present a repetitive pattern (such as day/night cycles for example) since the basis functions are sinusoids. However, their efficiencies decrease when data are less regular, especially on the modelisation of derivatives. Wavelet basis is designed to settle this sensibility to irregular signals. Coefficients are slightly longer to compute, but this basis has really good mathematical properties and progressively replaces Fourier basis in several applications [29,30]. For non periodic data, the classical choice is spline basis, particularly the cubic splines in practice [6]. B-splines are piecewise polynomial functions and require few coefficients to define a good approximation, which make B-splines especially adequate when observations are sparse on the time domain [31]. They allow for approximating a wide range of shapes with a rather good smoothness [30]. From a computational point of view, one can use the R package fda, on which one can find methods to fit observations into functional data, and way more tools for FDA. An overview of the fda package can be found in [30].

Once the data set is approximated by functions, one may perform analysis on them, and some classical statistical tools have been extended in the functional context. One of the first and most important adapted methods was the functional principal component analysis (FPCA). Although slightly different, FPCA provides analogous information as the finite dimensional version [27]. This method allows for describing data into a non correlated low dimensional space. This is why it provides an excellent explanatory tool to visualize main features of the data as well as a way to reduce the number of informative dimensions. This can be particularly useful when one wants to apply algorithms on the vector $\{{\alpha }_1,\dots ,{\alpha }_N\}$ of coefficients of the basis expansion, with N rather large. It may accelerate calculation while retaining most of the information as well as avoiding the curse of dimension in a big data context. We may also cite several methods presented in [27] such as functional canonical correlation, discriminant analysis and functional linear models.

The purpose of this paper is twofold: at first, it aims at providing a brief review of several methods and references for the theoretical aspects. Secondly, examples of practical tools and useful packages (on the software R as it is currently the most convenient to perform FDA) of curve clustering state-of-the-art methods are presented. Then, we also detail a specific study on a real data set, coming from our collaboration with the French Swimming Federation. This work focuses on the clustering of performance progression curves of young male swimmers and uses several FDA tools. We emphasise the fact that FDA provides some tools that give information we could not exhibit otherwise, like the study of derivatives for example.

1.4. Clustering Functional Data

In this article, we emphasise the clustering approach, often fundamental when exploring a new data set or beforehand to a forecast. This method consists of computing sub-groups of individuals on a data set that makes sense in the context of the study. Given K as number of clusters, a clustering algorithm would apply one or several rules to gather individuals presenting common properties. This problem has been largely explored these past ten years in the functional context and we will give some elements to summarize the state-of-the-art. According to the survey [28], functional data clustering algorithms can be sorted in three distinct families, detailed below. We do not develop on direct clustering on raw observational points that does not take into account functional nature of the data and may give poor results.

$(i)$ 2-step methods. The first step consists of the fitting procedure we detailed previously, choosing a common basis for all data. Then, a clustering algorithm such as k-means [31], or hierarchical clustering methods for example, is performed on the basis coefficients. If this vector of coefficients is in a high dimension, one can add a step of FPCA and perform the clustering on the scores coming from the first eigenfunctions of the FPCA.

$(ii)$ Non-parametric clustering. An overview of non-parametric functional data analysis is provided by [32]. It details many aspects where one does not assume that functional observations can be defined by a finite number of parameters. The idea is to define a distance between the functional observations without assumptions on the form of the curves. A classical measure of proximity between functions $x_i$ and $x_j$ is defined as:

$$d_l(x_i,x_j)={\left({\int }_{\mathcal{T}}{x}_i^{(l)}(t)-x_j^{(l)}(t)dt\right)}^{\frac{1}{2}},$$

(2)

where $x_i^{(l)}$ is the l-th derivative of x. With such a measure of distance, one can run the heuristic of the k-means, for example, or any other distance-based clustering.

$(iii)$ Model-based clustering. This approach has been widely developed in the past years and gives good results. As the 2-step approach, it often uses basis expansion and/or FPCA to fit the data. However, rather than proceeding in two-step, the clustering is performed simultaneously. Many algorithms are based on Gaussian mixture models coupled with an EM-algorithm to compute the parameters [33,34,35]. We chose in this study to adapt the algorithm FunHDDC presented in [35] for several reasons that we develop in the following Materials and Methods section. Note that the literature does not give specific indications about the family of methods that should be used in a specific context and one might test several of them. Nevertheless, one should keep in mind that the right way to fit the data into functions strongly depends on the structure of the data. We also give some additional references in the next section, where we detail some algorithms that are easy to use in practice because of their implementation within an unified R package. Below, Figure 1 from [28] summarizes the different families described above and the process of clustering in a functional context:

2. Materials and Methods

2.1. Description of the Real Swimming Data Set

First of all, two types of data sets, on which we performed functional clustering algorithms, are described. The way we simulated data sets to test several methods will be described at the end of the current section. The real data have been collected by the French Swimming Federation. It gathers all the performances of French male swimmers, since 2002, for the 100 m freestyle in a 50 m pool. Because of confidentiality issues, athletes are identified by a number. The data set is composed of 46,115 performances and the ages of 1468 different swimmers, and is available on the Github page of the corresponding author. Raw data consists of time series of competition performances at different ages for each swimmer. The number of competitions and the age at which swimmers participate differs from one to another, leading to strongly uneven time series. This particularity of the data set (as well as the ability to work on derivatives) led to modelling the observations as functions rather than time series. Thus, a first step of fitting was performed to extract the functional nature of the data and deal with the random fluctuations in the observations. All of the algorithms were run on the R software and the corresponding packages will be named in the sequel.

2.2. Testing Several Algorithms on Simulated Data Sets

To begin, a comparative study of several classical functional clustering algorithms has been performed on simulated data. Little information is provided on the algorithms, but we invite readers to refer to the corresponding papers for details. For this work, the R package funcy, which compiles seven state-of-the-art algorithms, was used. It gives a common syntax and format for the input and output data. The list below enumerates the algorithms, regrouped according to their family, that can be used with funcy.

(i)

distance-based:

• distclust: An approximation of the $L^2$ distance between curves is defined, and a k-means heuristic is used on individuals using this distance. This method is well designed in the context of sparsely observed functions with irregular measurements [36].

(ii)

model-based:

• fitfclust: One of the first algorithms to use a Gaussian mixture model for univariate functions that we briefly describe. This heuristic holds for all following algorithms described as Gaussian mixture methods. Functions are represented using basis functions, and the associated coefficients are supposed to come from Gaussian distributions. Given a number K of different means and covariances parameters corresponding to the K clusters, an EM algorithm is used to estimate the probability of each observational curves to belong to a cluster. When the iterations stop (various stopping criteria exhist), an individual is affected to its most likely cluster. A preliminary step of FPCA can be added to work on lower dimensional vectors and thus speed up the calculations. This method is well designed in the context of sparsely observed functions [37].
• iterSubspace: A non-parametric model based algorithm. This method uses the Karhunen–Loeve expansion of the curves, and perform a k-means algorithm on the scores of FPCA and the mean process. This method can be useful when the Gaussian assumption does not hold but k-means approach can lead to unstable results [38].
• funclust: A Gaussian mixture model based algorithm. This method uses the Karhunen–Loeve expansion of the curves and allows each cluster’s Gaussian parameters to be of different sizes, according to the quantity of variance expressed by the corresponding FPCA. The algorithm also allows different covariance structures between clusters and thus generalizes some methods such as iterSubspace [33].
• funHDDC: A Gaussian mixture model based algorithm. This method presents lots of common characteristics with funclust, but additionally allows clustering of multivariate functions. The algorithm proposes six ways to model covariates structures, especially for the extra-dimension of the FPCA [35].
• fscm: A non-parametric model based algorithm. Each cluster is modeled by a Markov random field, and functions are clustered by shape regardless to the scale. Observation curves are considered as locally-dependent, and a K-nearest neighbors algorithm is used to define the neighborhood structure. Then, an EM algorithm estimates parameters of the model. This method is well designed when the assumption of independence between curves does not hold [38].
• waveclust: A linear Gaussian mixed effect model algorithm. This approach uses a dimension reduction step using wavelet decomposition (rather than classic FPCA). An EM algorithm is used to compute parameters of the model and probabilities to belong to a cluster. This method is well designed for high-dimension curves, when variations such as peaks appears in data, and thus wavelets perform better than splines [29].

Unfortunately, the current version (1.0.0) of the funcy package has some trouble with the funHDDC algorithm, which is not directly usable at the moment. All of the remaining algorithms were applied on three simulated data sets, with $K=4$ groups. The resulting clustering were compared to real group distributions using the Rand Index (RI) [39]. This measure, between 0 and 1, is computed by counting according pairs of individuals between two different partitions of a data set. The RI is provided as a result of the funcit function of the funcy package, and compares the ability of each procedure to retrieve the actual groups. Then, graphs of centres of each curve clusters were drawn to analyse consistency of our results according to the original data.

2.3. Clustering the Real Swimming Data Set

As mentioned above, the real data set is very irregular, with no accordance in time and in number of measurements between athletes. Thus, the first step of the analysis was the definition of a common ground through a smoothing procedure. According to the non-periodic form of the data and the relatively low sampling of observational points (around 30) for each athlete, a B-spline basis was chosen. The study focuses on the age period from 12 to 20 years old, which is crucial in the progression phenomenon that we aimed at studying. A basis of seven B-splines of order 4 was defined so that the derivatives remain smooth enough to work on derivatives. Since we did not wish to focus on a specific time period, the knots were equally placed on ages 13 to 19. One should note that data are considered as realisations of a stochastic process, and thus raw data are assumed to contain random fluctuations. The function that is fitted using the B-spline basis has to represent properly the true signal and the well known over/under-fitting issue appears in this case. In order to differentiate the true signal from the noise, several methods can be used, knowing that there is always a trade-off between smoothness of the function and closeness to observation points. A classical approach consists of the use of penalisation in the least-square fitting calculation, and the signal-to-noise ratio would be controlled by a unique hyper-parameter. In our case, we used a cross-validation criterion to compute an optimal value for this hyper-parameter, and the resulting functional data were considered as coherent by swimming experts. This whole fitting procedure was performed thanks to R (version 3.5.0) software, and especially the fda (version 2.4.8) package. To efficiently analyse a real data set, one needs first to explore it, in order to figure out the more suitable algorithm to use. To this purpose, an FPCA was performed on the progression curves and their derivatives, separately. We looked at the percentage of variance explained by each eigenfunction and the shapes of them, to understand the main features of the curves. One can see in Figure A1 of the appendix that main variations among level of performance appear at young ages and a clustering procedure on progression curves tends to simply group individuals according to this criterion. As displayed on Figure A2, first eigenfunctions of the derivatives represent three different modes of variations localized at young, middle, and older ages. These characteristics of data would be relevant for including in the clustering procedure in addition to the level of performance information. For this purpose, the funHDDC algorithm was used as clustering procedure, as this is one of the rare implemented algorithms that works in a multivariate case and thus allows for considering both curves and their derivatives simultaneously. One can find more details in the results section about the reasons of this choice. Although implemented in the funcy package, we chose to work with the original funHDDC R package because of current problems of implementation on it. Several features of the package were used, as Bayesian Information Criterion (BIC), Integrated Classification Likelihood (ICL) and slope heuristic, to deal with problems of model selection and choice of the number K of clusters. Since no particular assumptions were made on the covariance structure or the number of clusters forming a sport expert point of view, the hyper-parameters of the model have been optimised from data. All possible models were computed for different values of K and the best one (the sense of the term best is developed in the Results section) was retained as our result clustering. In the funHDDC algorithm, each cluster is considered to be fully characterised by a Gaussian vector, from which scores on eigenfunctions of the FPCA are assumed to come. Thus, the clustering becomes a likelihood maximization problem where one wants to find value of means and covariance matrices that fit the best to data, as well as probabilities for each of data curves to belong to a cluster. All parameters influence the values of each other and this classical issue is addressed thanks to an Expectation–Maximization (EM) algorithm that computes efficiently close approximations of optimal parameters. At the end of the procedure, a data curve is considered to belong to the cluster within which it has the higher probability to come from. The clustering was performed on the curves and their derivatives, separately at first. Then, the resulting clusters were compared thanks to the Adjusted Rand Index (ARI) [39], which is an extended version of the RI to partitions with different numbers of clusters. This measure allows for quantifying the adequacy between individuals grouped whether by a clustering on progression curves or on derivatives. Note that many other indexes exist, such as the Silhouette index or Jaccard index for example. Although our results were quite comparable using one or another, the reader can find an extensive comparative study of the different idexes in [40]. Noticing that athletes were clustered differently, providing two types of information, we decided to perform a third clustering procedure. This time, the multivariate clustering version on the funHDDC algorithm was used. The term multivariate clustering refers to a clustering algorithm that deals with multidimensional functions. The progression curves were defined as a first variable, with the derivatives as a second variable. For each clustering procedure, the resulting clusters’ centres and curves were plotted. Finally, the results were analysed and discussed with swimming experts to confront the found clusters to the sport logic.

2.4. Definition of the Simulated Data Sets

We defined three simulated data sets to test the algorithms of the funcy package on different contexts. We used the function sampleFuncy of the funcy package that provides an easy way to simulate data sets suited to apply methods from funcy directly on them.

Simulated data sets are sampled from four different processes of the form $f(t)+\epsilon$, with f and $ϵ$ detailed in

Table 1. Details on the simulated samples. Processes are defined as $f(t)+\epsilon$ with four different functions f in each sample and a varying noise parameter $ϵ$.

Data Set	Functions	Noise	Observations on t-Axis
Sample 1	$t⟼t-1$ $t⟼t^2$ $t⟼t^3$ $t⟼\sqrt{t}$	$\epsilon \sim \mathcal{N}(0,0.05)$	10 points at regular instants
Sample 2	$t⟼t-1$ $t⟼t^2$ $t⟼t^3$ $t⟼\sqrt{t}$	$\epsilon \sim \mathcal{N}(0,0.1)$	10 points at regular instants
Sample 3	$t⟼t-1$ $t⟼-t^2$ $t⟼t^3$ $t⟼sin(2\pi t)$	$\epsilon \sim \mathcal{N}(0,0.5)$	≤ 10 points at irregular instants

below. For each process, 25 curves are simulated, thereby leading to 100 curves in each sample. The aim of the following clustering procedure is to gather themselves curves that correspond to the same underlying process. An additional goal would be to retrieve, at least approximately, the shapes of deterministic functions f that generated each data curves within a cluster. Intuitively, Sample 1 depicts an easy situation with low noise and well separated processes, whereas Sample 2 represents the same processes in a higher variance context. Finally, Sample 3 corresponds to a high-noise and crossing processes context, which is designed to be trickier. Moreover, in the case of Sample 3, observations of the curves are irregular on the t-axis and thus, for three out of six algorithms of the package that are not implemented in this case, we had to proceed to a previous fitting step. We used the function regFuncy of the funcy package to this purpose.

3. Results

3.1. Results on Simulated Data

Table 2. Mean Rand Index and (Standard Deviation) on 100 simulations of the tree samples. Each algorithm run in at most a few seconds on our simulated data sets. Comparison in speed between algorithms is given as a multiple of the fastest which is set arbitrarily to 1.

Method	Sample 1	Sample 2	Sample 3	Running Speed
fitfclust	0.945 (0.14)	0.857 (0.01)	0.307 (0.06)	2.8
distclust	0.996 (0.01)	0.888 (0.05)	0.523 (0.07)	19.2
iterSubspace	0.938 (0.14)	0.850 (0.12)	0.527 (0.07)	1
funclust	0.450 (0.17)	0.418 (0.16)	0.084 (0.07)	1
fscm	0.948 (0.12)	0.902 (0.01)	0.527 (0.07)	7
waveclust	0.920 (0.12)	0.810 (0.01)	0.324 (0.13)	34

below provides results on the comparison between the six algorithms of the funcy package. These results are mainly illustrative and one should be aware that the quality of a clustering algorithm cannot be addressed through simulation. However, it can give some clues on the type of situations where algorithms seem to perform properly or not. Sample 1 was designed to be easy to cluster and most model based algorithms perform well. Nevertheless, they are outperformed by the only distance based method distclust that gives almost perfect results. As Sample 2 is simply a noisier version of Sample 1, the problem becomes harder and results slightly decrease. One can note that, although the stochastic processes we sampled from are the same as in Sample 1, the “hierarchy” between methods changes. This might indicate differences at noise robustness between the methods. For example, performances of the fcsm algorithm decrease only slightly compared to distclust. Finally, as expected, the results fall on the fuzzy situation of Sample 3. Only three methods achieve moderate performances, and one can note that there is an algorithm of both families among them. Although Table 2 gives information about the performances of these algorithms, it does not give information on the ability of the methods to retrieve the actual shape of the underlying functions. The following graphs will add some visual evidence to judge the quality of the results.

Figure 2 gives one representation of the Sample 1 curves. In addition, the curves of each clusters’ centres of the best performing algorithm are drawn. One can see that Sample 1 is quite simple to deal with, since curves of different groups are well separated. Not surprisingly, the distclust clustering algorithm satisfyingly figures out the actual shape of each process.

One can see in Figure 3 that, if the noisier situation of Sample 2 affects the good clustering rate, the shapes of the underlying functions remain correctly approximated by clusters’ centres of fscm.

Sample 3 was designed to be trickier since curves cross each other and the signal appears rather noisy. In this context, one can see in Figure 4 that, as expected, the algorithms retrieve approximately the true shapes of the underlying functions. While the sinus (in black) function seems correctly identified, the iterSubspace algorithm struggles to separate the polynomial functions.

3.2. Data Set of Swimmers’ Progression Curves

The choice of the funHDDC algorithm was motivated by two main arguments. First, this is a flexible method that has been shown efficient in various cases—secondly, because of the results of the FPCA performed to explore the data set. Indeed, as presented in the top of Figure A1 (Appendix A), we notice that the underlying dimension of the data seems clearly lower than the original one: the entire variance of the data set can be expressed with only three scores. Additionally, the shapes of the first informative eigenfunctions are drawn (bottom Figure A1) and inquire about the main features of the data. One can see an analogous result of low underlying dimension for the derivatives (Appendix A: Figure A2). Thus, it seems natural to work with a FPCA-based method. FunHDDC provides a flexible way to deal with the “extra-dimensions”, proposing six models that represent six different ways to model covariance matrices. We tested each of them to figure out the more appropriate. As advised by the authors in [34], the BIC is used for the model selection and the slope heuristic to choose the number K of clusters. According to these criteria, the best model, among the six, is composed of five clusters for the progression curves, and four clusters for the derivatives. Resulting clusters are represented in Figure A3 and Figure A4 (Appendix A). At this stage, the Adjusted Rand Index (ARI) is used to compare the way athletes were grouped and give a value of 0.41. The value of ARI would be around 0.20 for a completely random clustering procedure. This result, far from an ARI equal to 1 of complete adequacy, lets us think that different features of the data were used to group individuals in each context. A discussion with swimming experts leads us to conclude that the clustering on progression curves mainly grouped athletes according to their level of performance, whereas the derivatives clustering seems to gather individuals presenting similar trends of progression (at a particular age, or with the same dynamic for example). These conclusions guided us to the multivariate clustering procedure, which gives results presented in Figure 5 and Figure 6. A close look at the groups in Figure 5 seems to indicate that multivariate clustering clusters combines information both on level of performance and trends of evolution. One can see that similar profiles are coloured the same way. We also verify this from a swimming expert point of view by checking samples of athletes in each groups. In Figure 6, one can see more clearly differences between each group thanks to the cluster centres’ curves.

4. Discussion

As mentioned in the simulated data set context, we shall emphasise that no objective criterion might reflect correctly the quality of a clustering procedure. The authors of [41] recall that all clustering algorithms are some way subjective regarding how they gather individuals or which metric they use. Thus, the resulting clusters should be judged and analysed according to the context. Like many other statistical tools, a clustering procedure does not give any quantitative certainty, but rather a new point of view on the data. One should consider as good results any useful perspective hidden in the raw data. Thus, we worked closely with sport experts, not only to analyse the results but throughout the entire analysis. All choices of parameters and/or methods were driven both by mathematical and sport considerations.

In this work, we provide enlightenment on some classical methods and useful practical packages as well as provide some clues on the particularities of the different algorithms. One can note that distance-based methods are generally easy to use and give rather good results for simple problems. On the other hand, model-based methods rely on more complicated design but often give good results for a wider range of problems. It explains why they are often recommended by experts of the field [28] and form most of the algorithms implemented in funcy. Algorithms using Gaussian mixtures are naturally more flexible than methods like k-means, since they might be considered as a generalisation with elliptic clusters rather than circular ones. However, one should also keep in mind that this flexibility often requires longer computational time. Indeed, even if the EM algorithm is really efficient to solve the mixture of Gaussian problem, the multiplicity of models and the number of clusters to test might take non-negligible time to run (few hours in our case). For our purpose, which is to help a swimming federation with the detection of young promising athletes, computational time was not an issue since the aim was more long-term decision-making. Nevertheless, many sport-related problems today need to be solved quickly or even live, and our methodological choices would have been different under such constraints.

Regarding the results on the swimming data set, we observe consistent outcomes from both mathematical and sport point of views. If our work does not give any certainty about the progression phenomenon of young swimmers, it sheds some light on its general pattern and provide a practical tool to gather similar profiles. Moreover, using FDA, we were able to figure out information from uneven time series. Using smooth functions instead of raw data points provides a first understanding of the main trends and the continuous nature of the progression phenomenon. However, one should always pay attention to the random fluctuations of the data that serve to fit the studied functions. In order to improve the quality of the approximation and decrease the influence of the noise, we would like to collect more data on swimmers, with training performances for example. Nevertheless, these results might help the detection of promising young athletes with both a better understanding and graphical outcomes to support the decision process. Note that this work remains descriptive and thus preliminary, but one can think of it as a first step for a further predictive analysis. If we do not discuss here findings about any particular swimmers for confidentiality concerns, we can highlight some points that seem interesting to swimming experts. First, as mentioned in [3,24], it seems difficult to precisely detect young talents before 16 years old because of the fast evolution before this age. One can observe between 14 and 16 years old a huge decrease of the value of the derivatives and thus of the speed of progression. Moreover, athletes that seem to be better at 20 years old are often those who continue to progress, even slightly, after 16 years old. A classical pattern, confirmed with swimming experts, is the presence of a cluster of swimmers who are always among best performers. These athletes are typically often detected and can benefit from the best conditions to improve their performances. However, two clusters of athletes, often slightly slower than previous ones when young, present opposite behaviours. As one group stops rapidly progressing and performs rather modestly at 20 years old, another cluster gathers swimmers with a rapid improvement who often perform as good as the best swimmers when older. One can think of these young athletes as the main target of a detection program, since they often remain away from top level structures at young ages. If these findings are promising, this work needs further development to provide more quantitative and predictive outcomes. The FDA offers several methods of classification and regression, but, as mentioned many times previously, it would be necessary to adapt them to our specific problem, or to develop new algorithms.

5. Conclusions

To conclude, we recall that the main purpose of this paper is to present a brief review of the functional data analysis and we emphasise one last time on the usefulness of such an approach. As supported by the example of curves clustering, FDA can offer new perspectives in the sport science field.