Coupling Elephant Herding with Ordinal Optimization for Solving the Stochastic Inequality Constrained Optimization Problems
Abstract
:1. Introduction
2. Stochastic Inequality Constrained Optimization Problems
2.1. Mathematical Formulation
2.2. Difficulty of the Problem
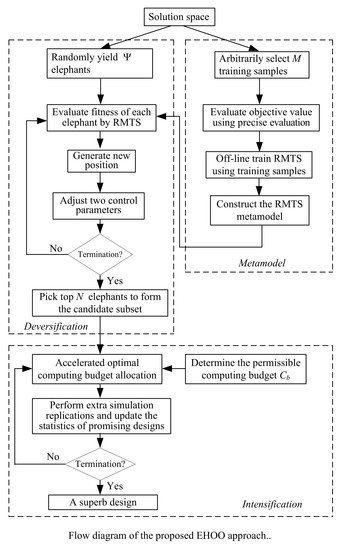
3. Solution Method
3.1. Metamodel Construction
3.2. Diversification
| Algorithm 1: The IEHO |
| Step 1: Configure parameters Configure the values of I, K, , , , , , , and set , where expresses the iteration counter. Step 2: Initialize clan (a) A population of I clans is initialized with positions For For For where denotes a random value generated in the range between 0 and 1, and denote the upper bound and lower bound of the solution variable, respectively. (b) Calculate the fitness of each elephant assisted by RMTS, , . Step 3: Ranking Rank the individuals in the ith clan based on their fitness from low to high, then determine the elite elephant and the worst elephant in the ith clan. Step 4: Clan updating Generate positions of the elite elephant by (12), and the others by (11). For , do For , do For , do If Else is a random value generated in the range between 0 and 1. If , set , and if , set . Step 5: Separating Generate positions of the worst elephant . For , do For , do Step 6: Update scale factors Step 7: Elitism
Step 8: Termination If , stop; else, set and go to Step 3. |
3.3. Intensification
| Algorithm 2: The AOCBA |
| Step 0. Set the quantity of , , ,…, , where expresses the iteration counter. Determine the value of . Step 1: If , stop and choose the optimum with the smallest objective value; else, go to Step 2. Step 2: Raise an extra computing budget () to , and update the simulation replications by Step 3: Execute extra simulation replications (i.e., ) for the th promising solution, then calculate the mean () and standard deviation () of these extra simulation replications using Step 4: Update the mean () and standard deviation () of overall simulation replications for the th promising solution using |
3.4. The EHOO Approach
| Algorithm 3: The EHOO |
| Step 0: Configure the parameters of , I, K,, , , , , , , , and . Step 1: Arbitrarily select x’s from the solution space and evaluate , then off-line train the RMTS using these training samples. Step 2: Arbitrarily choose ’s as the initial population and apply Algorithm 1 to these individuals assisted by RMTS. After Algorithm 1 terminates, rank all the final ’s based on their approximate fitness from low to high and choose the prior ’s to be the significant solutions. Step 3: Employ Algorithm 2 to the significant solutions and find the optimum , and this one is the superb solution that we seek. |
4. Application to Staffing Optimization of a Multi-Skill Call Center
4.1. A One-Period Multi-Skill Call Center
4.2. Problem Statement
4.3. Mathematical Formulation
4.4. Employ the EHOO Approach
4.4.1. Construct the Metamodel
4.4.2. Apply the IEHO Associated with the Metamodel
4.4.3. Obtain the Superb Solution
5. Simulation Results
5.1. Simulation Examples and Test Results
5.2. Comparisons
 , solid line with circles
, solid line with circles  , and solid line with crosses
, and solid line with crosses  , respectively. Table 5 reveals that the average best-so-far objective values computed by PSO, GA and ES were 2.54%, 5.71% and 3.96% larger than that obtained by EHOO, respectively. The average best-so-far objective values determined by three competing approaches were worse not only than that obtained by EHOO with case = 40, but also than those obtained by other three cases of . Simulation results show that the EHOO approach can determine superb solutions in an acceptable time and outperforms the three competing approaches. As long as the three competing approaches continue to proceed for a very long time, it is reasonable to obtain better results than the proposed approach.
, respectively. Table 5 reveals that the average best-so-far objective values computed by PSO, GA and ES were 2.54%, 5.71% and 3.96% larger than that obtained by EHOO, respectively. The average best-so-far objective values determined by three competing approaches were worse not only than that obtained by EHOO with case = 40, but also than those obtained by other three cases of . Simulation results show that the EHOO approach can determine superb solutions in an acceptable time and outperforms the three competing approaches. As long as the three competing approaches continue to proceed for a very long time, it is reasonable to obtain better results than the proposed approach.6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Lejeune, M.A.; Margot, F. Solving chance-constrained optimization problems with stochastic quadratic inequalities. Oper. Res. 2016, 64, 939–957. [Google Scholar] [CrossRef]
- Lan, H.Y. Regularization smoothing approximation of fuzzy parametric variational inequality constrained stochastic optimization. J. Comput. Anal. Appl. 2017, 22, 841–857. [Google Scholar]
- Bhatnagar, S.; Hemachandra, N.; Mishra, V.K. Stochastic approximation algorithms for constrained optimization via simulation. ACM Trans. Model. Comput. Simul. 2011, 21, 15. [Google Scholar] [CrossRef]
- Hussain, K.; Salleh, M.N.M.; Cheng, S.; Shi, Y.H. On the exploration and exploitation in popular swarm-based metaheuristic algorithms. Neural Comput. Appl. 2019, 31, 7665–7683. [Google Scholar] [CrossRef]
- Yang, X.S.; Deb, S.; Zhao, Y.X.; Fong, S.M.; He, X.S. Swarm intelligence: Past, present and future. Soft Comput. 2018, 22, 5923–5933. [Google Scholar] [CrossRef] [Green Version]
- Ryerkerk, M.; Averill, R.; Deb, K.; Goodman, E. A survey of evolutionary algorithms using metameric representations. Genetic Program. Evolvable Mach. 2019, 20, 441–478. [Google Scholar] [CrossRef]
- Wang, G.G.; Deb, S.; Gao, X.Z.; Coelho, L.D. A new metaheuristic optimisation algorithm motivated by elephant herding behavior. Int. J. Bio-Inspired Comput. 2016, 8, 394–409. [Google Scholar] [CrossRef]
- Elhosseini, M.A.; el Sehiemy, R.A.; Rashwan, Y.I.; Gao, X.Z. On the performance improvement of elephant herding optimization algorithm. Knowl.-Based Syst. 2019, 166, 58–70. [Google Scholar] [CrossRef]
- Peska, L.; Tashu, T.M.; Horvath, T. Swarm intelligence techniques in recommender systems—A review of recent research. Swarm Evol. Comput. 2019, 48, 201–219. [Google Scholar] [CrossRef]
- Piotrowski, A.P.; Napiorkowski, M.J.; Napiorkowski, J.J.; Rowinski, P.M. Swarm intelligence and evolutionary algorithms: Performance versus speed. Inf. Sci. 2017, 384, 34–85. [Google Scholar] [CrossRef]
- Ho, Y.C.; Zhao, Q.C.; Jia, Q.S. Ordinal Optimization: Soft Optimization for Hard Problems; Springer: New York, NY, USA, 2007. [Google Scholar]
- Hwang, J.T.; Martins, J.R.R.A. A fast-prediction surrogate model for large datasets. Aerosp. Sci. Technol. 2018, 75, 74–87. [Google Scholar] [CrossRef]
- Tang, J.H.; Wang, W.; Xu, Y.F. Two classes of smooth objective penalty functions for constrained problems. Numer. Funct. Anal. Optim. 2019, 40, 341–364. [Google Scholar] [CrossRef]
- Horng, S.C.; Lin, S.S. Embedding advanced harmony search in ordinal optimization to maximize throughput rate of flow line. Arab. J. Sci. Eng. 2018, 43, 1015–1031. [Google Scholar] [CrossRef]
- Horng, S.C.; Lin, S.S. Embedding ordinal optimization into tree-seed algorithm for solving the probabilistic constrained simulation optimization problems. Appl. Sci. 2018, 8, 2153. [Google Scholar] [CrossRef] [Green Version]
- Horng, S.C.; Lin, S.S. Bat algorithm assisted by ordinal optimization for solving discrete probabilistic bicriteria optimization problems. Math. Comput. Simul. 2019, 166, 346–364. [Google Scholar] [CrossRef]
- Yu, K.G. Robust fixture design of compliant assembly process based on a support vector regression model. Int. J. Adv. Manuf. Technol. 2019, 103, 111–126. [Google Scholar] [CrossRef]
- Erdik, T.; Pektas, A.O. Rock slope damage level prediction by using multivariate adaptive regression splines (MARS). Neural Comput. Appl. 2019, 31, 2269–2278. [Google Scholar] [CrossRef]
- Sambakhe, D.; Rouan, L.; Bacro, J.N.; Goze, E. Conditional optimization of a noisy function using a kriging metamodel. J. Glob. Optim. 2019, 73, 615–636. [Google Scholar] [CrossRef]
- Han, X.; Xiang, H.Y.; Li, Y.L.; Wang, Y.C. Predictions of vertical train-bridge response using artificial neural network-based surrogate model. Adv. Struct. Eng. 2019, 22, 2712–2723. [Google Scholar] [CrossRef]
- Bouhlel, M.A.; Hwang, J.T.; Bartoli, N.; Lafage, R.; Morlier, J.; Martins, J.R.R.A. A Python surrogate modeling framework with derivatives. Adv. Eng. Softw. 2019, 135, 102662. [Google Scholar] [CrossRef] [Green Version]
- Hassanien, A.E.; Kilany, M.; Houssein, E.H.; AlQaher, H. Intelligent human emotion recognition based on elephant herding optimization tuned support vector regression. Biomed. Signal Process. Control 2018, 459, 182–191. [Google Scholar] [CrossRef]
- Kowsalya, S.; Periasamy, P.S. Recognition of Tamil handwritten character using modified neural network with aid of elephant herding optimization. Multimed. Tools Appl. 2019, 78, 25043–25061. [Google Scholar] [CrossRef]
- Meena, N.K.; Parashar, S.; Swarnkar, A.; Gupta, N.; Niazi, K.R. Improved elephant herding optimization for multiobjective DER accommodation in distribution systems. IEEE Trans. Ind. Inform. 2018, 14, 1029–1039. [Google Scholar] [CrossRef]
- Chen, C.H.; Lee, L.H. Stochastic Simulation Optimization: An Optimal Computing Budget Allocation; World Scientific: Hackensack, NJ, USA, 2010. [Google Scholar]
- Yu, M.; Chang, C.G.; Zhao, Y.; Liu, Y. Announcing delay information to improve service in a call center with repeat customers. IEEE Access 2019, 7, 66281–66291. [Google Scholar] [CrossRef]
- Ibrahim, S.N.H.; Suan, C.L.; Karatepe, O.M. The effects of supervisor support and self-efficacy on call center employees’ work engagement and quitting intentions. Int. J. Manpow. 2019, 40, 688–703. [Google Scholar] [CrossRef]
- Avramidis, A.N.; Chan, W.; L’Ecuyer, P. Staffing multi-skill call centers via search methods and a performance approximation. IIE Trans. 2009, 41, 483–497. [Google Scholar] [CrossRef]
- SimOpt.org, One Period, Multi-Skill Call Center. [Online]. 2016. Available online: http://simopt.org/wiki/index.php?title=Call_Center (accessed on 19 March 2020).
- Ryan, T.P. Sample Size Determination and Power; John Wiley and Sons: Hoboken, NJ, USA, 2013. [Google Scholar]
- Wang, Q.X.; Chen, S.L.; Luo, X. An adaptive latent factor model via particle swarm optimization. Neurocomputing 2019, 369, 176–184. [Google Scholar] [CrossRef]
- Delice, Y. A genetic algorithm approach for balancing two-sided assembly lines with setups. Assemb. Autom. 2019, 39, 827–839. [Google Scholar] [CrossRef]
- Spettel, P.; Beyer, H.G. A multi-recombinative active matrix adaptation evolution strategy for constrained optimization. Soft Comput. 2019, 23, 6847–6869. [Google Scholar] [CrossRef]






| Call Type | Agent Groups | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 440 | 1 | 3 | 4 | 5 | 7 | 8 | 9 | 11 | 12 | |||
| 2 | 540 | 3 | 6 | 7 | 8 | 11 | 12 | ||||||
| 3 | 440 | 2 | 4 | 6 | 7 | 9 | 10 | 11 | 12 | ||||
| 4 | 540 | 5 | 10 | 12 | |||||||||
| 5 | 440 | 8 | 9 | 10 | 11 | 12 | |||||||
| Call Type | Agent Groups | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 240 | 1 | 3 | 5 | 7 | 9 | ||||||||||
| 2 | 240 | 1 | 11 | 13 | 15 | |||||||||||
| 3 | 160 | 2 | 4 | 6 | 8 | 10 | ||||||||||
| 4 | 260 | 4 | 12 | 14 | ||||||||||||
| 5 | 130 | 1 | 2 | 5 | 11 | |||||||||||
| 6 | 230 | 3 | 7 | 8 | 10 | |||||||||||
| 7 | 260 | 5 | 9 | 12 | 13 | |||||||||||
| 8 | 130 | 5 | 6 | 10 | 12 | 14 | 15 | |||||||||
| 9 | 260 | 2 | 4 | 5 | 6 | 10 | ||||||||||
| 10 | 125 | 5 | 6 | 9 | 13 | 14 | ||||||||||
| 11 | 235 | 1 | 5 | 8 | 10 | 12 | ||||||||||
| 12 | 155 | 4 | 9 | 11 | 14 | 15 | ||||||||||
| 13 | 230 | 2 | 5 | 7 | 10 | 15 | ||||||||||
| 14 | 260 | 3 | 8 | 9 | 13 | 15 | ||||||||||
| 15 | 225 | 2 | 6 | 7 | 14 | |||||||||||
| 16 | 130 | 1 | 5 | 10 | 12 | |||||||||||
| 17 | 160 | 2 | 6 | 11 | ||||||||||||
| 18 | 130 | 3 | 4 | 13 | 14 | |||||||||||
| 19 | 260 | 2 | 8 | 12 | 15 | |||||||||||
| 20 | 260 | 3 | 6 | 8 | 12 | 13 | 14 | |||||||||
| [17,18,17,16,18,17,16,17,16,16,17,17]T | |
| 0.80, 0.93, 0.86, 0.93, 0.51, 0.78 | |
| COST | 253.9 |
| CPU time (sec.) | 24.67 |
| N | Cost | CPU Times (sec.) | ||
|---|---|---|---|---|
| 40 | [22,22,22,22,23,23,22,23,22,22,23,23,22,23,22]T | 538 | 0.80 | 115.65 |
| 30 | [23,22,23,22,23,22,22,23,23,22,23,23,22,22,22]T | 539.1 | 0.81 | 112.34 |
| 20 | [22,22,23,23,23,22,23,23,22,22,22,23,22,23,22]T | 539.3 | 0.82 | 109.51 |
| 10 | [22,23,22,22,23,22,22,23,22,23,23,23,22,23,22]T | 539.7 | 0.82 | 107.47 |
| Approaches | ABO † | |
|---|---|---|
| EHOO, CASE = 40 | 538.6 | 0 |
| PSO with accurate evaluation | 552.3 | 2.54% |
| GA with accurate evaluation | 569.4 | 5.71% |
| ES with accurate evaluation | 559.9 | 3.96% |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Horng, S.-C.; Lin, S.-S. Coupling Elephant Herding with Ordinal Optimization for Solving the Stochastic Inequality Constrained Optimization Problems. Appl. Sci. 2020, 10, 2075. https://doi.org/10.3390/app10062075
Horng S-C, Lin S-S. Coupling Elephant Herding with Ordinal Optimization for Solving the Stochastic Inequality Constrained Optimization Problems. Applied Sciences. 2020; 10(6):2075. https://doi.org/10.3390/app10062075
Chicago/Turabian StyleHorng, Shih-Cheng, and Shieh-Shing Lin. 2020. "Coupling Elephant Herding with Ordinal Optimization for Solving the Stochastic Inequality Constrained Optimization Problems" Applied Sciences 10, no. 6: 2075. https://doi.org/10.3390/app10062075