Self-Insulating Joint Design for Live-Line Operation Based on the Cable-Driven Parallel-Series Mechanism

Abstract

This paper proposes a self-insulating joint design based on the cable-driven parallel-series (CDPS) mechanism and electrical insulation analysis. The design provides the motions, mechanic support, and electrical insulation for robotic arms in live-line operation, which can maintain the equipment without manual intervention and power interruption. This CDPS mechanism can integrate four degrees of freedom (DOFs) motion in one joint, while the traditional series joint can only realize one DOF independently. The cable forces in the CDPS are calculated by the inverse kinematics to ensure the safe and flexible operation of the mechanism. The self-insulating joint has certain advantages over other designs because the electrical insulation is integrated into the joint instead of the traditional extra insulation layer. This integration reduces the weight of the arm mechanic structure. In addition, the structural complexity and weight are further reduced by separating the actuators and motors from the joint by using CDPS. Electric field distribution near the joint is calculated by the charge simulation method to analyze the insulation performance under the voltage of 35 kV. The cable forces and electric field distribution of the mechanism are measured to validate the simulation models. The inverse kinematics and insulation models of the self-insulating joint can provide detailed information for the mechanic and insulation design of the robotic arms.

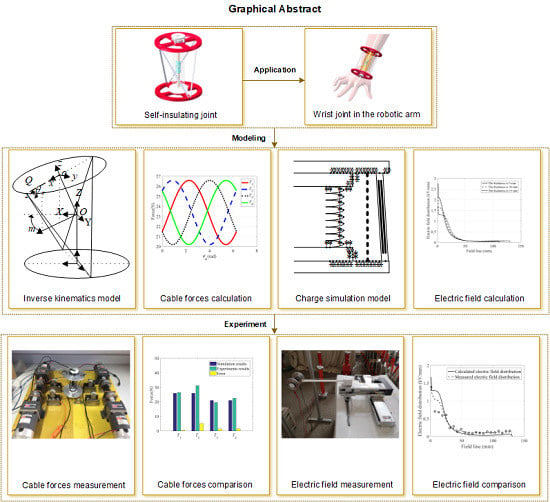
1. Introduction

Live-line operation and maintenance have been extensively performed in power systems because the aging phenomena of the electrical power equipment become severe while the cost of power interruption continuously increases [1,2,3]. The live-line teleoperated robots gradually replace the manual transmission line and substation operation because the manual operation is risky for the personnel and inefficient for the line and substation equipment maintenance [4,5,6].

Since the 1980s, Wakizako et al. developed the first generation of master-slave live-line operation robots Phase I; the operator was required to operate the robotic arm in the insulating bucket at the end of the lifting mechanism to complete the live-line operation task [7]. Then, the Phase-I robot was modified and upgraded to Phase II by integrating the machine visual system, automatic tool switch device, and human–machine interface. The Phase-II robot could complete all operation tasks at the same insulation level as Phase I with the semi-automatic operation strategy [8]. Maddahi et al. compared the performances of the teleoperated manipulators with and without a haptic device, and they concluded that the task completion time reduced when the haptic generated the force [9]. The aforementioned live-line teleoperated robots adopt the independent insulation layer connected to the robotic arm to provide body electrical isolation. This method has reliable insulation performance for the transmission live-line operation because the insulation layer is thick enough to ensure sufficient leakage distance to prevent flashover under the contaminated conditions. Therefore, the structure of the system is excessively large and complicated for the substation equipment maintenance with limited operating space. This paper proposes a design scheme of a self-insulating joint as a wrist in the robotic arm based on the cable-driven parallel-series (CDPS) mechanism to control the motion in four degrees of freedom (DOFs). The CDPS design can provide more than one DOF to improve the flexibility of the joint, which facilitates the robotic arm to accomplish complicated live-line operation in a restricted workspace. The mechanism separates the motors and actuators from the joint to realize the remote driving. The electrical insulation is integrated into the joint to reduce the volume and complexity of the mechanics.

The CDPS was initially used to mimic the movement of the human neck. In 2007, Nori et al. proposed a mechanism to simulate a human cervical vertebra by a compression spring and the muscles of the neck by cables. This model provided an approximate equivalent calculation method for the lateral bending of the flexible spring [10]. Then, Gao et al. focused on the low-noise humanoid neck robot and investigated the CDPS with a flexible spine support. The paper also optimized the mechanism design and analyzed the workspace [11]. Lim examined a similar model by replacing the flexible spine with a rigid spine and optimized the cable force distribution [12]. Yigit et al. modified the CDPS mechanism by adding two concentric shafts connected with a universal joint in the spring to restrict the lateral bending motion of the spring and simplify the model. The concentric shafts are driven by the motor in the mechanism to provide the yaw motion [13]. Mustafa and Chen considered multiple CDPS mechanisms as the wrist, elbow, and shoulder joints to compose a seven DOF robotic arm [14,15]. The dimension of a cable-driven parallel system was then optimized based on tension distributions [16,17,18]. Boschetti conducted further research to minimize the consequences of cable failure by generating a wrench opposite to the motion direction [19,20,21]. In 2019, the CSPS mechanisms are used for the rehabilitation and under water applications due to their intrinsic flexibility and adaptability [22,23]. In addition, the modified continuum mechanism derived from CDPS are combined with the circumnutation strategy to explore a complex and unstructured environment [24,25,26,27]. Based on previous research, the proposed modified joint combines the advantages from [11] and [13], adopting four cables in the CDPS mechanism to enable the yaw rotation around the z-axis without an additional motor in the mechanism.

The electrical insulation of the mechanism is provided by the insulating plates and shafts. The charge simulation method (CSM) is used to calculate the electric field distribution around the CDPS mechanism. The maximum electric field strength is used to evaluate the insulation performance between the upper and lower platforms. The ring charge in the CSM can reduce the computational complexity for the axis-symmetrical geometry [28,29,30]. In addition, the electric field distribution is measured to compare with the simulation results based on Pockels effect because the optical probe is rarely affected by the environment interference.

The self-insulated joint can imitate the wrist in the robotic arm for live-line operation in substation equipment maintenance. The CDPS joint separates the motors and actuators from the robotic arm to increase the insulation margin and reduce the weight. The proposed CDPS mechanism with four crossed-connected cables has a specific advantage over current CDPS designs in terms of realizing an additional yaw motion with no auxiliary motor in the mechanism. The required forces in the cables increase when compared with the traditional series joint. The operational life of the CDPS joint is longer than the traditional series joint with the same load capacity and DOFs because the robotic arm requires four traditional series joints to realize the motions in four DOFs. The joint at the end of the arm provides mechanic support for the other three joints and endures more mechanic stress. The electrical insulation structures are further improved by replacing the traditional insulation layer with the self-insulating joint and arm. This paper focuses on the mechanic and insulation design of the joint. We first presented the inverse kinematics model of the CDPS joint mechanism to compute the cable forces. Then, we calculated the electric field distribution near the mechanism to analyze the insulation performance. The models are verified by experiments, which measure the cable forces and electric field during live-line operation.

2. Cable-Driven Parallel-Series Mechanism

The proposed CDPS mechanism is applied as the flexible wrist joint in the robotic arm (Figure 1a). The connecting rods are made of composite insulating materials to provide sufficient load capacity and electrical insulation. All the motors and actuators drive the joint through four polypropylene cables to increase the insulation margin and reduce the weight of the robotic arm.

Figure 1b shows the detailed structure of the CDPS mechanism composed of a lower platform and an upper platform. A compression spring is set between the lower and upper platforms in the concentric position to provide the mechanic support. The structure is further supported by two concentric shafts in the spring connected by a universal joint. The upper shaft is made of insulating material and passes through the upper platform, so the shaft restricts the lateral bending of the compression spring, which effectively simplifies the modeling and calculation of the inverse kinematics. Two insulating plates are attached to the upper and lower platforms to provide the electrical insulation. A combined bearing connects the upper moving platform with the insulating plate to separately realize the rotation and translation motion. The structure is driven by four cables to realize four DOFs, which provide the roll, pitch, yaw DOFs by the parallel mechanism, and a translational motion along the upper shaft by the series mechanism to adjust the flexibility. The four cables are actuated by four remote motors and pass through four holes on the upper and lower platforms.

2.1. Model Details of the Mechanism

To model the motion of the proposed CDPS mechanism, a simplified structure schematic diagram is established according to the mechanism model, as shown in Figure 2. This structure is divided into five parts to illustrate the modeling details.

(1)

Four cables are modeled with negligible mass and diameter in the inverse kinematics model. The fixed points of the cables on the lower and upper platforms are defined as P₁, P₂ and Q₁, Q₂. The corresponding relationship between the four cable numbers and the fixed points on the platform is shown in Figure 2. In the initial state, the fixed-point connection line of the moving platform is perpendicular to the connection line of the base. The distances of P and Q to the concentric points of the upper and lower platforms are p and q, respectively. The length of the cable between Q and P is defined as L. T is the force of the cable. The unit vector along the direction of the cable is defined as u_i.

(2)

The lower platform is considered the fixed reference, and its thickness is neglected. O₁X₁Y₁Z₁ is defined as the local coordinate system, and origin O₁ is located at the center of the platform. The Y₁ axis is along the direction of O₁P₂. The X₁ axis is perpendicular to the Y₁ axis. The Z₁ axis is determined by the right-hand principle based on the X₁ and Y₁ axes. An insulation plate is attached to the upper surface of the lower platform to provide electrical insulation for the live-line operation.

(3)

The upper platform is the movable part of the mechanism, and its thickness is neglected. oxyz is defined as the local coordinate system; origin o is located at the geometric center of the moving platform. The x-axis is along the oQ₂ direction, and the y-axis is perpendicular to the x-axis. The z-axis is determined by the right-hand principle based on the x and y axes. An insulation plate is attached to the bottom surface of the upper platform to provide electrical insulation for the live-line operation.

(4)

The cylindrical compression spring connects the concentric lower and upper platforms. The force and torque generated by the cylindrical compression spring support the load and participate in the movement of the upper platform. The combined bearing between the spring and the moving platform rotates around the z-axis and moves along the z-axis. Therefore, the spring does not participate in the z-axis rotation and only rotates in the oxy plane providing the roll and pitch angles.

(5)

Two shafts connected by a universal joint in the spring restricts the lateral bending motion of the structure to simplify the inverse kinematics model of the spring lateral bending motion. The upper shaft passes the center of the moving platform through the combined bearing, and the lower shaft is fixed at the center of the lower platform. The upper and lower shafts are perpendicular to the two platforms. A global coordinate system OXYZ is defined at the center of the universal joint with identical axis directions to the local coordinate system O₁X₁Y₁Z₁. The distances from the global origin O to the local origins O₁ and o are defined as d₁ and d₂. d₁ is equal to the length of the lower shaft, and d₂ is variable because the upper shaft is connected with the upper platform by the linear bearing, which slides along the upper shaft during the motion. The upper shaft is made of an insulating material to provide the electrical insulation between the upper and lower platforms.

The mechanism design rotates the upper platform in three axes with pitch, roll, and yaw angles by adding another cable instead of installing the motor in the z-axis compared to the traditional mechanism driven by three cables. A tangential pulling tension is provided by four cables to enable the upper platform rotating around the z-axis with the rotation bearing.

The homogeneous coordinates of P₁ and P₂ in the global coordinate system OXYZ on the lower platform are:

$${}_{}{}^O\mathit{p}{}_1={\left(0,-p,-d_1,1\right)}^T,{}_{}{}^O\mathit{p}{}_2={\left(0,p,-d_1,1\right)}^T.$$

(1)

Similarly, the homogeneous coordinates of Q₁ and Q₂ in the local coordinate system oxyz on the upper platform are:

$${}_{}{}^o\mathit{q}{}_1={\left(-q,0,0,1\right)}^T,{}_{}{}^o\mathit{q}{}_2={\left(q,0,0,1\right)}^T.$$

(2)

Three angles are selected as the parameters to describe the upper platform motion in three axes and transfer the matrix from the local coordinate system to the global coordinate system. o′ is the projection of o on the OXY plane. θ_m is the angle between o′O and the OX axis to describe the spring bending direction on the plane OXY. θ_b is the angle between two shafts to describe the bending degree of the spring on the plane oOO′. θ_r is the anticlockwise rotation angle around the z-axis to describe the yaw angle of the upper platform in the local coordinate system. p and q are the radius of the upper and lower platforms (Figure 2).

Rotation matrix R from the local coordinate system to the global coordinate system is obtained using Rodriguez formula,

$$\mathit{R}=e^{\widehat{i}{\theta }_b}=\mathit{I}+\widehat{\mathit{i}}\sin {\theta }_b+{\widehat{\mathit{i}}}^2\left(1-\cos {\theta }_b\right)=\left[\begin{array}{ccc}{s}_{110}& s_{120}& s_{130}\\ s_{210}& s_{220}& s_{230}\\ s_{310}& s_{320}& s_{330}\end{array}\right],$$

(3)

$$\begin{array}{l}{s}_{110}={\sin }^2{\theta }_m+\cos {\theta }_b{\cos }^2{\theta }_m\\ s_{120}=s_{210}=\left(\cos {\theta }_b-1\right)\cos {\theta }_m\sin {\theta }_m\\ s_{130}=-s_{310}=\sin {\theta }_b\cos {\theta }_m\\ s_{230}=-s_{320}=\sin {\theta }_b\sin {\theta }_m\\ s_{220}={\cos }^2{\theta }_m+\cos {\theta }_b{\sin }^2{\theta }_m\\ s_{330}=\cos {\theta }_b\end{array},$$

(4)

where

$$\mathit{i}={\left[-\sin {\theta }_m,\cos {\theta }_m,0\right]}^T,$$

(5)

$$\widehat{\mathit{i}}=\left[\begin{array}{ccc}0& 0& \cos {\theta }_m\\ 0& 0& \sin {\theta }_m\\ -\cos {\theta }_m& -\sin {\theta }_m& 0\end{array}\right],$$

(6)

$${\mathit{R}}_h=\left[\begin{array}{cccc}{s}_{110}& s_{120}& s_{130}& 0\\ s_{210}& s_{220}& s_{230}& 0\\ s_{310}& s_{320}& s_{330}& 0\\ 0& 0& 0& 1\end{array}\right].$$

(7)

The coordinates are translated along the z-axis by the length of d₂ in M_trans:

$${\mathit{M}}_{trans}=\left[\begin{array}{cccc}1& 0& 0& 0\\ 0& 1& 0& 0\\ 0& 0& 1& d_2\\ 0& 0& 0& 1\end{array}\right].$$

(8)

The rotation matrix M_{rot_oz} around the z-axis is

$${\mathit{M}}_{rot\_oz}=\left[\begin{array}{cccc}\cos {\theta }_r& -\sin {\theta }_r& 0& 0\\ \sin {\theta }_r& \cos {\theta }_r& 0& 0\\ 0& 0& 1& 0\\ 0& 0& 0& 1\end{array}\right].$$

(9)

The transformation matrix ^OT_o from the local coordinate system to the global coordinate system is obtained by combining the three transformation matrices above:

$${}_{}{}^O\mathit{T}{}_o={\mathit{R}}_h{\mathit{M}}_{trans}{\mathit{M}}_{rot\_oz}=\left[\begin{array}{cccc}{s}_{11}& s_{12}& s_{13}& a\\ s_{21}& s_{22}& s_{23}& b\\ s_{31}& s_{32}& s_{33}& c\\ 0& 0& 0& 1\end{array}\right],$$

(10)

where

$$\begin{array}{l}{s}_{11}=\cos {\theta }_r\left(\cos {\theta }_b{\cos }^2{\theta }_m+{\sin }^2{\theta }_m\right)-\cos {\theta }_m\sin {\theta }_m\sin {\theta }_r\left(\cos {\theta }_b-1\right),\\ s_{12}=\cos {\theta }_m\cos {\theta }_r\sin {\theta }_m\left(\cos {\theta }_b-1\right)-\sin {\theta }_r\left(\cos {\theta }_b{\cos }^2{\theta }_m+{\sin }^2{\theta }_m\right),\\ s_{13}=\cos {\theta }_m\sin {\theta }_b,\\ s_{21}=\sin {\theta }_r\left({\cos }^2{\theta }_m+\cos {\theta }_b{\sin }^2{\theta }_m\right)+\cos {\theta }_m\cos {\theta }_r\sin {\theta }_m\left(\cos {\theta }_b-1\right),\\ s_{22}=\cos {\theta }_r\left({\cos }^2{\theta }_m+\cos {\theta }_b{\sin }^2{\theta }_m\right)-\cos {\theta }_m\sin {\theta }_m\sin {\theta }_r\left(\cos {\theta }_b-1\right),\\ s_{23}=\sin {\theta }_b\sin {\theta }_m,\\ s_{31}=-\sin {\theta }_b\sin {\theta }_m\sin {\theta }_r-\cos {\theta }_m\cos {\theta }_r\sin {\theta }_b,\\ s_{32}=\cos {\theta }_m\sin {\theta }_b\sin {\theta }_r-\cos {\theta }_r\sin {\theta }_b\sin {\theta }_m,\\ s_{33}=\cos {\theta }_b,\\ a=d_2\sin {\theta }_b\cos {\theta }_m,\\ b=d_2\sin {\theta }_b\sin {\theta }_m,\\ c=d_2\cos {\theta }_b.\end{array}$$

2.2. Inverse Kinematics and Static Solution

The lengths of four cables l = [l₁, l₂, l₃, l₄] are calculated in the inverse kinematics model based on the angles and the length of d₂:

$$\mathit{l}=f\left(\mathit{x}\right),f:{\mathit{R}}^4\to {\mathit{R}}^4,$$

(11)

where x = [θ_m, θ_b, θ_r, d₂]^T∈R⁴.

The length of the cable is calculated by the following distance Formula (12) according to the transformation matrix:

$$\mathit{l}=\Vert {}_{ }{}^O\mathit{p}-{}_{ }{}^O\mathit{T}{}_o{}_{ }{}^o\mathit{q}\Vert .$$

(12)

Transformation matrix ^oT_O from the global coordinate system to the local coordinate system is shown in Label (13):

$${}_{}{}^o\mathit{T}{}_O=\left[\begin{array}{cccc}{s}_{11}& s_{21}& s_{31}& -a\\ s_{12}& s_{22}& s_{32}& -b\\ s_{13}& s_{23}& s_{33}& -c\\ 0& 0& 0& 1\end{array}\right].$$

(13)

The position of the cable holes on the lower platform in the local coordinate system is as follows:

$$\begin{array}{cc}\hfill {}_{}{}^o\mathit{p}{}_1=& {}_{}{}^o\mathit{T}{}_O\cdot {}_{}{}^O\mathit{p}{}_1\hfill \\ \hfill =& [-p\cdot s_{21}-d_1\cdot s_{31}-a,-p\cdot s_{22}-d_1\cdot s_{32}-b,\hfill \\ & {-p\cdot s_{23}-d_1\cdot s_{33}-c,1]}^T\hfill \end{array}$$

(14)

$$\begin{array}{c}{}_{}{}^o\mathit{p}{}_2={}_{}{}^o\mathit{T}{}_O\cdot {}_{}{}^O\mathit{p}{}_2=(p\cdot s_{21}-d_1\cdot s_{31}-a,p\cdot s_{22}-d_1\cdot s_{32}-b,\\ {p\cdot s_{23}-d_1\cdot s_{33}-c,1)}^T\end{array}$$

(15)

$${}_{}{}^o\mathit{q}{}_1={\left(-q,0,0,1\right)}^T,{}_{}{}^o\mathit{q}{}_2={\left(q,0,0,1\right)}^T.$$

(16)

Due to the angular limitation of the mechanism bending, the spring provides a support force F_k along the direction of the upper shaft and perpendicular to the moving platform. The force of the spring is calculated by Hooke’s law,

$$F_k=K\left(l-l_0\right),$$

(17)

where K is the elastic coefficient of the spring, l is the length of the spring, and l₀ is the initial length of the spring.

For the upper platform, the combined force of the four driving cables is decomposed into component forces F₁ and F₂ in the direction of the upper shaft and the plane of the upper platform, respectively (Figure 3).

Figure 3 shows that F₁ cancels the force of the spring F_k. F₂ is the force subjected from the upper platform to the upper shaft. Therefore, the torque balance equation of the upper shaft is achieved between F₂ and the gravity of the upper platform:

$$Mg\sin {\theta }_b\cdot d_2=F_2{d}_2,$$

(18)

where M is the mass of the upper platform.

The torque and force balance equations of the upper platform are shown in Labels (20) and (21):

$${{\displaystyle \sum }}_{i=1}^4{T}_i{}_{}{}^o\mathit{u}={\left[-F_2\cos \left({\theta }_r-{\theta }_m\right),F_2\sin \left({\theta }_r-{\theta }_m\right),F_k\right]}^T,$$

(19)

$${{\displaystyle \sum }}_{i=1}^4{}_{}{}^o\mathit{r}\times T{}_{}{}^o\mathit{u}={\left[m_x,m_y,m_z\right]}^T,$$

(20)

where m_x, m_y, and m_z are the component of the combined torque along the x-axis, y-axis, and z-axis, respectively. T_i represents the force on each cable:

$${}_{}{}^o\mathit{u}=\left({}_{}{}^o\mathit{T}{}_O\cdot {}_{}{}^O\mathit{p}{}_2-{}_{}{}^o\mathit{q}{}_1\right)/\Vert {}_{}{}^o\mathit{T}{}_O\cdot {}_{}{}^O\mathit{p}{}_2-{}_{}{}^o\mathit{q}{}_1\Vert ,$$

$$\begin{array}{c}{}_{}{}^o\mathit{r}{}_1={}_{}{}^o\mathit{r}{}_3={\left[-q,0,0,1\right]}^T,\\ {}_{}{}^o\mathit{r}{}_2={}_{}{}^o\mathit{r}{}_3={\left[q,0,0,1\right]}^T.\end{array}$$

According to the characteristics of the spring-shaft structure, the torque balance equation must be achieved along the z-axis because the combined torque on the oxy plane is zero when the mechanism is in the static state. Therefore, three force balance equations and one torque balance equation along the z-axis are obtained because the torques m_x and m_y are canceled by the interaction between the shaft and the upper platform:

$$\left[\begin{array}{cccc}{M}_1& M_2& M_3& M_4\end{array}\right]\cdot \left[\begin{array}{c}{T}_1\\ T_2\\ T_3\\ T_4\end{array}\right]=\left[\begin{array}{c}-F_2\cos \left({\theta }_r-{\theta }_m\right)\\ F_2\cos \left({\theta }_r-{\theta }_m\right)\\ F_k\\ 0\end{array}\right],$$

(21)

where

$$\begin{array}{c}{M}_1=\left[\begin{array}{c}q-a-d_1{s}_{31}-p{s}_{21}\\ -b-d_1{s}_{32}-p{s}_{22}\\ -c-d_1{s}_{33}-p{s}_{23}\\ q\left(b+d_1{s}_{32}+p{s}_{22}\right)\end{array}\right],\\ M_2=\left[\begin{array}{c}-q-a-d_1{s}_{31}-p{s}_{21}\\ -b-d_1{s}_{32}-p{s}_{22}\\ -c-d_1{s}_{33}-p{s}_{23}\\ -q\left(b+d_1{s}_{32}+p{s}_{22}\right)\end{array}\right],\\ M_3=\left[\begin{array}{c}q-a-d_1{s}_{31}+p{s}_{21}\\ -b-d_1{s}_{32}+p{s}_{22}\\ -c-d_1{s}_{33}+p{s}_{23}\\ q\left(b+d_1{s}_{32}-p{s}_{22}\right)\end{array}\right],\\ M_4=\left[\begin{array}{c}q-a-d_1{s}_{31}+p{s}_{21}\\ -b-d_1{s}_{32}+p{s}_{22}\\ -c-d_1{s}_{33}+p{s}_{23}\\ -q\left(b+d_1{s}_{32}-p{s}_{22}\right)\end{array}\right].\end{array}$$

3. Mechanism Insulation Analysis

Since the cable-driven parallel-series mechanism is used as the joint of the robotic arm for live-line operation, the insulation performance of the joint is essential to protect the safety of the mechanism operator and power equipment. The CSM has been used to analyze the potential and electric field distribution of the mechanism. The ring charges are used in the platforms, insulating plates, and conductive springs due to their axis-symmetrical geometries. The line charges are used to fit the shape of the insulating cables. The contour points are set to the interfaces between different materials to satisfy the boundary conditions. The schematic for the insulator analysis is shown in Figure 4. The electric field distribution is calculated and measured along the field line with a 10 mm gap to the insulating plate.

The charge value is calculated by the following equation:

$$\left[Q\right]={\left[P\right]}^{-1}\left[V\right],$$

(22)

where P is the potential or field coefficient matrix, Q is the simulating charge array, and V is the values of contour points on the interfaces between different materials.

The insulating plates and insulating cables are considered the insulating materials in the mechanism to provide the mechanic support and electric insulation. The charges and contour points on the interface between the platform and these solid insulating materials satisfy the following boundary condition:

$${\displaystyle \sum }_{i=1}^{n_e+n_a}{P}_{ij}{Q}_j=V,$$

(23)

where n_e and n_a are the numbers of charges in the electrode and air, respectively; P_ij is the potential coefficient; Q_j is the simulating charge; V is the potential on the interface between the electrode and the insulating materials.

The charges and contour points on the interface between the platform satisfy the following boundary condition:

$${\displaystyle \sum }_{i=1}^{n_e+n_i}{P}_{ij}{Q}_j=V,$$

(24)

where n_i is the number of charges in the insulating plate; V is the potential on the interface between the electrode and air.

The charges and contour points on the interface between the solid insulating materials and air satisfy the following condition to satisfy Dirichlet and Neumann boundary conditions:

$${\displaystyle \sum }_{i=1}^{n_e+n_i}{P}_{ij}{Q}_j-{\displaystyle \sum }_{i=1}^{n_e+n_a}{P}_{ij}{Q}_j=0,$$

(25)

$${\epsilon }_a{\displaystyle \sum }_{i=1}^{n_e+n_i}{f}_{ij}{Q}_j-{\epsilon }_r{\displaystyle \sum }_{i=1}^{n_e+n_a}{f}_{ij}{Q}_j=0,.$$

(26)

where f_ij is the normal flux density coefficient; ε_r and ε_a are the relative permittivities of the insulating material and air, respectively.

The charges and contour points on the interface between the insulating plate and the conductive spring satisfy the following boundary condition:

$${\displaystyle \sum }_{i=1}^{n_e+n_s+n_a}{P}_{ij}{Q}_j=V_s,$$

(27)

where n_s is the number of charges in the conductive spring; V_s is the unknown floating potential of the spring.

The charges and contour points on the interface between the air and the conductive spring satisfy the following boundary condition:

$${\displaystyle \sum }_{i=1}^{n_e+n_s+n_i}{P}_{ij}{Q}_j=V_s.$$

(28)

Since the conductive spring is not energized, the enclosed charge inside each metal joint is equal to zero:

$${\displaystyle \sum }_{i=1}^{n_s}{Q}_j=0.$$

(29)

This model is used to calculate the electric potential and field distributions of the mechanism and analyze the insulation performance based on the maximum electric field strength.

4. Simulation Results and Discussion

4.1. Kinematics Simulation

The inverse kinematic model is used to analyze the upper platform motion in three axes driven by four cables of the proposed CDPS mechanism. Since the mechanism needs specific stiffness to ensure a fixed and steady state, the compression spring is compressed through the force provided by the cables. The pretightening forces of the cables are set at 23.5 N in the original state. The effect of θ_m on the forces of the four cables is analyzed when θ_b = π/30 and θ_r = 0. The range of θ_m is 0–2π.

Figure 5 indicates that the forces in four cables periodically vary with θ_m because the trajectory of the upper platform is a circle when θ_m increases from 0 to 2π.

The effect of θ_b on the forces of the four cables is analyzed when θ_m = 0 and θ_r = 0. The range of θ_b is 0–π/10.

Figure 6 shows that the forces of Cables 2 and 4 significantly increase with the increase in θ_b, while the forces of Cables 1 and 3 gradually decrease with the increase in θ_b. Cables 2 and 4 provide increasing proportion of the force to bend the spring from the initial state to the π/10 state. The nonlinear increasing tendency of the force is consistent with the characteristics of the spring.

The effect of θ_r on the forces of the four cables is analyzed when θ_m = 0 and θ_b = 0. The range of θ_r is 0–π/4.

The yaw angle motion of the mechanism is analyzed by changing θ_r from 0 to π/4. Figure 7 indicates that the forces in Cables 1 and 2 are identical to those in Cables 3 and 4 due to the axis symmetrical geometry of the mechanism.

4.2. Electrical Insulation Simulation

The electrical insulation performance is evaluated by the electric potential and field distribution near the CDPS mechanism in Figure 8 and Figure 9. The supply voltage is set to 35 kV, and the surface of the insulating plate is assumed to be dry and clean.

Figure 8 shows that the insulating plate near the upper platform sustains most of the potential and has a higher probability to discharge than other locations of the mechanism.

The electric field distributions with different thicknesses of the insulating plate are shown in Figure 9.

Since the integration of the electric field strength along the field line equals the same supply voltage, the maximum electric field strength is the critical factor to affect the air breakdown and discharge. The maximum values of three field distributions near the upper platform are 2.76 kV/mm, 2.13 kV/mm, and 1.67 kV/mm. The maximum electric field with a thickness of 15 mm is less than the dielectric strength of air. Since the dielectric strength of air is 2.1 kV/mm (RMS), the air corona discharge and breakdown occur with 5 and 10 mm insulating plates close to the upper platform where the electric field strength exceeds the dielectric strength of air. The discharge around the live-line operation robot can be observed in the withstand voltage test [31]. Therefore, the thickness of the insulating plates is selected as 15 mm to achieve reliable insulation performance.

5. Experiment Verifications

5.1. Kinematics Experiment

The CDPS mechanism is constructed to verify the inverse kinematic and dynamic models. The upper platform and lower platform are made of steel, while the upper shaft is made of epoxy to provide the electrical insulation. The cables are made of polypropylene to provide a strong endurance of the pulling stress and hydrophobic surface to prevent water films. Four motors with 2.12 Nm torque drive four cables to rotate the upper platform in three axes. The cable forces are measured to compare with the simulation results. The system setup is shown in Figure 10. The radius of the upper and lower platforms is 74 mm. The length of the upper and lower shafts is 50 mm. The insulating plate is 15 mm thick (Figure 10).

The forces of the cables are measured when the mechanism is set to different attitudes to compare the results of the simulation model. The attitude combinations are θ_m = π/2, θ_b = π/30, θ_r = 0; θ_m = 0, θ_b = π/10, and θ_r = 0; and θ_m = 0, θ_b = 0, and θ_r = π/4, respectively (Figure 11). The four columns in Figure 11 present the mechanism bending attitude in four planes (left, front, right, and top). The bending angles are marked in the figures to show the exact attitudes.

The errors between measured values and simulation results are calculated in Figure 12 when the mechanism maintains the attitude in Figure 11a.

The errors between measured values and simulation results are calculated in Figure 13 when the mechanism maintains the attitude in Figure 11b.

The errors between measured values and simulation results are calculated in Figure 14 when the mechanism maintains the attitude in Figure 11c.

In Figure 12, Figure 13 and Figure 14, the average error between simulation and experiment results is 7.18%. The error increases to 43.7% when the cable force increases to a relatively large value (T₂ and T₄). This increase occurs because the increasing friction between cables and platforms is neglected, and the cable elongation due to the large stress of the bending spring is not included in the model.

5.2. Electric Field Measurement

The electric field measurement experiment schematic is shown in Figure 15, and the experiment setup is shown in Figure 16.

The electric field measurement is composed by the electric field probe, optical fiber, and measuring system. The ball screw structure is used as the carrier of the electric field probe to adjust the distance between the probe and the CDPS mechanism. The electric field components in three axes are separately measured and integrated to compare with the simulation results.

The measured and calculated electric field distributions are compared in Figure 17. The average error is 9.57%, which proves that the simulation results are consistent with the experiment results. The error can be further decreased by performing the experiment in the shield room to eliminate the environment interference.

6. Conclusions

The self-insulating joint is developed for the robotic arms to maintain the live-line equipment in the substations. Both the kinematics and insulation performance of the joint are modeled to analyze the cable forces and electric field distributions. The proposed mechanism significantly reduces the weight, volume, and structural complexity by separating the motors and actuators from the joint, when comparing with the traditional live-line robotic arms.

• The traditional CDPS mechanism is modified to actuate the joint remotely by four polypropylene cables. This mechanism can realize four DOFs (roll, pitch, yaw, and translation) motions with no additional motor in the mechanism.
• Two insulating plates are attached to the upper and lower platforms to integrate the electrical insulation design into the joint. The insulation performance has been evaluated to ensure the safe operation of the joint under 35 kV AC voltage.