A Fast Multilevel Fuzzy Transform Image Compression Method
Abstract
:1. Introduction
2. Preliminaries
2.1. Discrete Dircct and Inverse F-Transforms for Coding/Decoding Images
- Ai(xi) = 1 for every i = 1, 2, …, n;
- Ai(x) = 0 if x is not in (xi−1, xi+1), where we assume x0 = x1 = a and xn+1 = xn = b by commodity of presentation;
- Ai(x) strictly increases on [xi−1, xi] for i = 2, …, n and strictly decreases on [xi, xi+1] for i = 1, …, n − 1;
- for every x ∈ [a,b].
- ▪
- n ≥ 3 and the nodes are equidistant, i.e., xi = a + h ∙ (i − 1) where h = (b − a)/(n − 1) for i = 1, 2, …, n;
- ▪
- Ai(xi − x) = Ai(xi + x) for every x ∈ [0,h] and i = 2, …, n − 1; and
- ▪
- Ai+1(x) = Ai(x − h) for every x ∈ [xi, xi+1] and i = 1,2, …, n − 1.
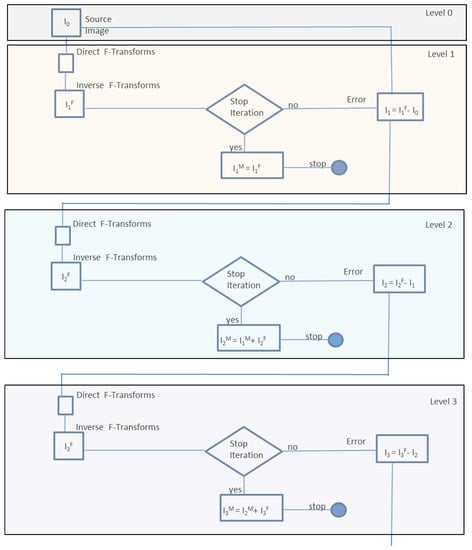
2.2. Multilevel F-Transform Image Compression
- The PSNR of the reconstructed image at Level h is greater than a prefixed threshold PSNRth. In this case, the quality of the reconstructed image obtained is already acceptable;
- The difference between the PSNR at the sth level and the PSNR at the (s − 1)th level is less than a difference threshold DPSNRth. The algorithm stops because the contribution to the improvement of the image quality obtainable in the subsequent iterations will be of little significance;
- The process has reached the maximum number of iterations smax.
3. The Fast Multilevel F-Transform Image Compression Method
| Algorithm 1: Fast MF-tr | ||
| Input: | N × M source image I0 Sorted set of compression ratios {ρ1, ρ2, …, ρn} Threshold similarityPSNRth Difference threshold DPSNRth Max number of iterations smax | |
| Output: | Reconstructed image | |
| 1 | ρ:= median({ρ1, ρ2, …, ρn}) | |
| 2 | ρBest: ρ | |
| 3 | stopIteration:= FALSE | |
| 4 | PSNRold:= PSNRth | |
| 5 | WHILE (stopIteration=FALSE) | |
| 6 | Compress the source image I0 via direct F-transform | |
| 7 | Decompress the source image I0 via inverse F-transform | |
| 8 | Calculate the PSNR index (8) | |
| 9 | IF (PSNR > PSNRth) AND (PSNRold < PSNRth) THEN | |
| 10 | ρBest: = ρold | |
| 11 | stopIteration:= TRUE | |
| 12 | ELSE | |
| 13 | IF (PSNR < PSNRth) AND (PSNRold > PSNRth) THEN | |
| 14 | ρBest:= ρ | |
| 15 | stopIteration:= TRUE | |
| 16 | ELSE | |
| 17 | PSNRold:= PSNR | |
| 18 | IF (PSNR > PSNRth) THEN | |
| 19 | ρ:= ρprev | |
| 20 | ELSE | |
| 21 | ρ:= ρnext | |
| 22 | END IF | |
| 23 | ENDIF | |
| 24 | END IF | |
| 25 | END WHILE | |
| 26 | CALL MF-tr(I0, PSNRth, PSNRth, DPSNRth, smax) | |
| 27 | RETURN reconstructed image | |
4. Test Results
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Perfilieva, I. Fuzzy transforms. Fuzzy Sets Syst. 2006, 157, 993–1023. [Google Scholar] [CrossRef]
- Di Martino, F.; Sessa, S. Compression and decompression of images with discrete fuzzy transforms. Inf. Sci. 2007, 17, 2349–2362. [Google Scholar] [CrossRef]
- Di Martino, F.; Loia, V.; Perfilieva, I.; Sessa, S. An image coding/decoding method based on direct and inverse fuzzy transforms. Int. J. Approx. Reason. 2008, 48, 110–131. [Google Scholar] [CrossRef] [Green Version]
- Di Martino, F.; Loia, V.; Sessa, S. Fuzzy transforms for compression and decompression of colour videos. Inf. Sci. 2010, 180, 3914–3931. [Google Scholar] [CrossRef]
- Perfilieva, I.; De Baets, B. Fuzzy transforms of monotone functions with application to image compression. Inf. Sci. 2010, 180, 3304–3315. [Google Scholar] [CrossRef]
- Di Martino, F.; Sessa, S. A Multi-Level Image Compression Method Based on Fuzzy Transforms. J. Ambient Intell. Humaniz. Comput. 2019, 10, 2745–2756. [Google Scholar] [CrossRef]
- Toet, A. A morphological pyramidal image decomposition. Pattern Recognit. Lett. 1989, 9, 255–261. [Google Scholar] [CrossRef]
- Paris, S.; Hasinoff, S.V.; Kautz, J. Local Laplacian filters: Edge-aware image processing with a Laplacian pyramid. Commun. ACM 2015, 58, 81–91. [Google Scholar] [CrossRef]
- Boiangiu, C.A.; Cotofana, M.V.; Naiman, A.; Lambru, C. A generalized Laplacian Pyramid aimed at image compression. J. Inf. Syst. Oper. Manag. 2016, 10, 327–335. [Google Scholar]
- Ispas, C.; Boiangiu, C.A. An image compression scheme based on Laplacian Pyramid. J. Inf. Syst. Oper. Manag. 2017, 11, 350–358. [Google Scholar]
- Walker, J.S.; Nguyen, T.Q. Wavelet-Based Image Compression (Chapter 6). In The Transform and Data Compression Handbook; Rao, K.R., Yip, P.C., Eds.; CRC Press LLC: Boca Raton, FL, USA, 2001. [Google Scholar]
- Song, M.-S. Wavelet Image Compression. Contemp. Math. 2006, 414, 41–73. [Google Scholar]
- Khan, U.R.; Ahmed, S.; Nazeer, T. Wavelet Based Image Compression Techniques: Comparative Analysis and Performance Evaluation. Int. J. Emerg. Technol. Eng. Res. 2017, 5, 9–13. [Google Scholar]
- Karthikeyan, C.; Palanisamy, C. An Efficient Image Compression Method by Using Optimized Discrete Wavelet Transform and Huffman Encoder. J. Comput. Theor. Nanosci. 2018, 15, 289–298. [Google Scholar] [CrossRef]
- Perfilieva, I. Fuzzy transform in image compression and fusion. Acta Math. Univ. Ostrav. 2007, 15, 27–37. [Google Scholar]
- Perfilieva, I.; Dankova, M. Image fusion on the basis of fuzzy transforms. In Proceedings of the 8th International FLINS Conference on Computational Intelligence in Decision and Control, Madrid, Spain, 21–24 September 2008; pp. 471–476. [Google Scholar]
- Manchanda, M.; Sharma, R. A novel method of multimodal medical image fusion using fuzzy transform. J. Vis. Commun. Image Represent. 2016, 40, 197–217. [Google Scholar] [CrossRef]
- Di Martino, F.; Sessa, S. Complete image fusion method based on fuzzy transforms. Soft Comput. 2019, 23, 2113–2123. [Google Scholar] [CrossRef]
- Huynh-Thu, Q.; Ghanbari, M. Scope of validity of PSNR in image/video quality assessment. Electron. Lett. 2008, 44, 800–801. [Google Scholar] [CrossRef]
- Huynh-Thu, Q.; Ghanbari, M. The accuracy of PSNR in predicting video quality for different video scenes and frame rates. Telecommun. Syst. 2012, 49, 35–48. [Google Scholar] [CrossRef]






| Algorithm | Levels | PSNR | SSIM | CPU Time (s) |
|---|---|---|---|---|
| MF-tr | 6 | 28.26 | 0.95 | 35.08 |
| Fast MF-tr | 2 | 28.29 | 0.96 | 17.57 |
| Algorithm | Levels | PSNR | SSIM | CPU Time (s) |
|---|---|---|---|---|
| MF-tr | 5 | 28.12 | 0.91 | 74.65 |
| Fast MF-tr | 2 | 28.10 | 0.92 | 33.28 |
| Algorithm | Levels | PSNR | SSIM | CPU Time (s) |
|---|---|---|---|---|
| MF-tr | 7 | 25.15 | 0.94 | 148.25 |
| Fast MF-tr | 3 | 25.16 | 0.94 | 59.86 |
| Size | Mean CPU Time (s) | ||
|---|---|---|---|
| MF-tr | Fast MF-tr | CPU Time Ratio | |
| 256 × 256 | 37.11 | 17.09 | 0.46 |
| 512 × 512 | 78.29 | 33.35 | 0.43 |
| 1024 × 1024 | 151.13 | 62.54 | 0.41 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Di Martino, F.; Perfilieva, I.; Sessa, S. A Fast Multilevel Fuzzy Transform Image Compression Method. Axioms 2019, 8, 135. https://doi.org/10.3390/axioms8040135
Di Martino F, Perfilieva I, Sessa S. A Fast Multilevel Fuzzy Transform Image Compression Method. Axioms. 2019; 8(4):135. https://doi.org/10.3390/axioms8040135
Chicago/Turabian StyleDi Martino, Ferdinando, Irina Perfilieva, and Salvatore Sessa. 2019. "A Fast Multilevel Fuzzy Transform Image Compression Method" Axioms 8, no. 4: 135. https://doi.org/10.3390/axioms8040135