Integro-Differential Equation for the Non-Equilibrium Thermal Response of Glass-Forming Materials: Analytical Solutions †
Abstract
:1. Introduction
2. Applicability of the Heat Equation with Dynamic Heat Capacity
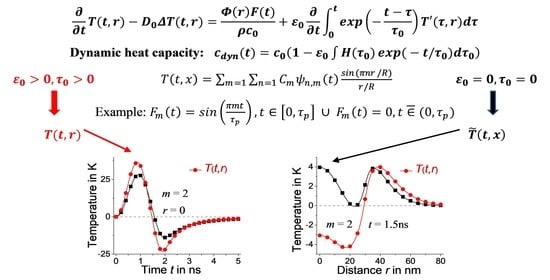
3. Heat Equation with Dynamic Heat Capacity
4. Heat Equation with Dynamic Heat Capacity: Plane Geometry
5. Heat Equation with Dynamic Heat Capacity: Spherical Geometry
6. Dependence of the Solution on the Distribution of Relaxation Times
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| Latin Symbols | |
| dynamic heat capacity (J·kg−1·K−1) | |
| initial part of (J·kg−1·K−1) | |
| equilibrium heat capacity (J·kg−1·K−1) | |
| thermal diffusivity (m2·s−1) | |
| sample thickness (m) | |
| heat flux time dependence (dimensionless) | |
| distribution function (s−1) | |
| heat release (J·kg−1) | |
| phonon mean-free-path (m) | |
| space variables (m) | |
| radius of spherical sample (m) | |
| radius of spherical heat source (m) | |
| time (s) | |
| solution to non-equilibrium heat equation (K) | |
| solution to conventional heat equation (K) | |
| non-equilibrium component of the solution (K) | |
| thickness of the flat heat source (m) | |
| Greek Symbols | |
| Kohlrausch coefficient (dimensionless) | |
| nth relaxation parameter (s−1) | |
| (dimensionless) | |
| Heaviside unit step function (dimensionless) | |
| thermal conductivity (W·K−1·m−1) | |
| nth relaxation parameter (s−1) | |
| density (kg·m−3) | |
| Kohlrausch relaxation time (s) | |
| time constant of nth component (s) | |
| Debye relaxation time (s) | |
| duration of the heating pulse (s) | |
| volumetric heat flux (W·m−3) | |
| heat flux space dependence (W·m−3) | |
| nth Fourier components (K/s) | |
| nth Fourier components (K) | |
| n,mth Fourier component (K) | |
Appendix A
References
- Birge, N.O.; Nagel, S.R. Specific-heat spectroscopy of the glass transition. Phys. Rev. Lett. 1985, 54, 2674–2677. [Google Scholar] [CrossRef] [PubMed]
- Herzfeld, K.F.; Litovitz, T.A. Absorption and Dispersion of Ultrasonic Waves; Academic Press Inc.: New York, NY, USA; London, UK, 1959. [Google Scholar]
- Korus, J.; Beiner, M.; Busse, K.; Kahle, S.; Unger, R.; Donth, E. Heat capacity spectroscopy at the glass transition in polymers. Thermochim. Acta 1997, 305, 99–110. [Google Scholar] [CrossRef]
- Beiner, M.; Korus, J.; Lockwenz, H.; Schröter, K.; Donth, E. Heat Capacity Spectroscopy Compared to Other Linear Response Methods at the Dynamic Glass Transition in Poly(vinyl acetate). Macromolecules 1996, 29, 5183–5189. [Google Scholar] [CrossRef]
- Huth, H.; Beiner, M.; Donth, E. Temperature dependence of glass-transition cooperativity from heat-capacity spectroscopy: Two post-Adam-Gibbs variants. Phys. Rev. B 2000, 61, 15092–15101. [Google Scholar] [CrossRef]
- Donth, E.-J. The Glass Transition; Springer Science and Business Media LLC: New York, NY, USA, 2001. [Google Scholar]
- Schneider, K.; Donth, E. Unterschiedliche Meßsignale am Glasübergang amorpher Polymere. 1. Die Lage der charakteristischen Frequenzen quer zur Glasübergangszone. Acta Polym. 1986, 37, 333–335. [Google Scholar] [CrossRef]
- Ediger, M.D.; Angell, C.A.; Nagel, S.R. Supercooled Liquids and Glasses. J. Phys. Chem. 1996, 100, 13200–13212. [Google Scholar] [CrossRef]
- Gotze, W.; Sjogren, L.B. Relaxation processes in supercooled liquids. Rep. Prog. Phys. 1992, 55, 241–376. [Google Scholar] [CrossRef]
- Hansen, C.; Stickel, F.; Berger, T.J.; Richert, R.; Fischer, E.W. Dynamics of glass-forming liquids. III. Comparing the dielectric α- and β-relaxation of 1-propanol and o-terphenyl. J. Chem. Phys. 1997, 107, 1086–1093. [Google Scholar] [CrossRef]
- Berthier, L.; Biroli, G. Theoretical perspective on the glass transition and amorphous materials. Rev. Mod. Phys. 2011, 83, 587–645. [Google Scholar] [CrossRef]
- Cangialosi, D. Dynamics and thermodynamics of polymer glasses. J. Phys. Condens. Matter 2014, 26, 153101. [Google Scholar] [CrossRef]
- Angell, C.A.; Ngai, K.L.; McKenna, G.B.; McMillan, P.F.; Martin, S.W. Relaxation in glassforming liquids and amorphous solids. J. Appl. Phys. 2000, 88, 3113–3157. [Google Scholar] [CrossRef] [Green Version]
- Smith, G.D.; Bedrov, D. Relationship between the α- and β-relaxation processes in amorphous polymers: Insight from atomistic molecular dynamics simulations of 1,4-polybutadiene melts and blends. J. Polym. Sci. Part B Polym. Phys. 2007, 45, 627–643. [Google Scholar] [CrossRef]
- Bock, D.; Petzold, N.; Kahlau, R.; Gradmann, S.; Schmidtke, B.; Benoit, N.; Rössler, E. Dynamic heterogeneities in glass-forming systems. J. Non-Cryst. Solids 2015, 407, 88–97. [Google Scholar] [CrossRef]
- Richert, R. Physical Aging and Heterogeneous Dynamics. Phys. Rev. Lett. 2010, 104. [Google Scholar] [CrossRef] [PubMed]
- Saiter-Fourcin, A.; Delbreilh, L.; Couderc, H.; Arabeche, K.; Schönhals, A.; Saiter, J.-M. Temperature dependence of the characteristic length scale for glassy dynamics: Combination of dielectric and specific heat spectroscopy. Phys. Rev. E 2010, 81, 041805. [Google Scholar] [CrossRef] [PubMed]
- Chua, Y.Z.; Young-Gonzales, A.R.; Richert, R.; Ediger, M.D.; Schick, C. Dynamics of supercooled liquid and plastic crystalline ethanol: Dielectric relaxation and AC nanocalorimetry distinguish structural α- and Debye relaxation processes. J. Chem. Phys. 2017, 147, 014502. [Google Scholar] [CrossRef]
- Chua, Y.Z.; Schulz, G.; Shoifet, E.; Huth, H.; Zorn, R.; Scmelzer, J.W.P.; Schick, C. Glass transition cooperativity from broad band heat capacity spectroscopy. Colloid Polym. Sci. 2014, 292, 1893–1904. [Google Scholar] [CrossRef]
- Chua, Y.Z.; Zorn, R.; Holderer, O.; Schmelzer, J.W.P.; Schick, C.; Donth, E. Temperature fluctuations and the thermodynamic determination of the cooperativity length in glass forming liquids. J. Chem. Phys. 2017, 146, 104501. [Google Scholar] [CrossRef]
- Richert, R. Heterogeneous dynamics in liquids: Fluctuations in space and time. J. Phys. Condens. Matter 2002, 14, R703–R738. [Google Scholar] [CrossRef]
- Larini, L.; Ottochian, A.; De Michele, C.; Leporini, D. Universal scaling between structural relaxation and vibrational dynamics in glass-forming liquids and polymers. Nat. Phys. 2007, 4, 42–45. [Google Scholar] [CrossRef]
- Voudouris, P.; Gomopoulos, N.; Le Grand, A.; Hadjichristidis, N.; Floudas, G.; Ediger, M.D.; Fytas, G. Does Brillouin light scattering probe the primary glass transition process at temperatures well above glass transition? J. Chem. Phys. 2010, 132, 074906. [Google Scholar] [CrossRef] [PubMed]
- Lubchenko, V.; Wolynes, P.G. Theory of Structural Glasses and Supercooled Liquids. Annu. Rev. Phys. Chem. 2007, 58, 235–266. [Google Scholar] [CrossRef] [Green Version]
- Pipkin, A.C. Lectures on Viscoelasticity Theory; Springer: Berlin/Heidelberg, Germany, 1986; ISBN 978-1-4612-1078-8. Available online: https://www.springer.com/gp/book/9780387963457 (accessed on 2 February 2021).
- Ikeda, M.; Aniya, M. Bond Strength—Coordination Number Fluctuation Model of Viscosity: An Alternative Model for the Vogel-Fulcher-Tammann Equation and an Application to Bulk Metallic Glass Forming Liquids. Matererials 2010, 3, 5246–5262. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Minakov, A.; Schick, C. Non-equilibrium fast thermal response of polymers. Thermochim. Acta 2018, 660, 82–93. [Google Scholar] [CrossRef]
- Minakov, A.; Schick, C. Nanometer scale thermal response of polymers to fast thermal perturbations. J. Chem. Phys. 2018, 149, 074503. [Google Scholar] [CrossRef]
- Minakov, A.; Schick, C. Nanoscale Heat Conduction in CNT-POLYMER Nanocomposites at Fast Thermal Perturbations. Molecules 2019, 24, 2794. [Google Scholar] [CrossRef] [Green Version]
- Noeiaghdam, S.; Sidorov, D.; Muftahov, I.R.; Zhukov, A.V. Control of Accuracy on Taylor-Collocation Method for Load Leveling Problem. Bull. Irkutsk. State Univ. Ser. Math. 2019, 30, 59–72. [Google Scholar] [CrossRef]
- Sidorov, D.; Muftahov, I.; Tomin, N.; Karamov, D.N.; Panasetsky, D.A.; Dreglea, A.; Liu, F.; Foley, A. A Dynamic Analysis of Energy Storage With Renewable and Diesel Generation Using Volterra Equations. IEEE Trans. Ind. Inform. 2020, 16, 3451–3459. [Google Scholar] [CrossRef] [Green Version]
- Noeiaghdam, S.; Dreglea, A.; He, J.-H.; Avazzadeh, Z.; Suleman, M.; Araghi, M.A.F.; Sidorov, D.; Sidorov, N.A. Error Estimation of the Homotopy Perturbation Method to Solve Second Kind Volterra Integral Equations with Piecewise Smooth Kernels: Application of the CADNA Library. Symmetry 2020, 12, 1730. [Google Scholar] [CrossRef]
- Wang, Y.; Ezz-Eldien, S.; Aldraiweesh, A.A. A new algorithm for the solution of nonlinear two-dimensional Volterra integro-differential equations of high-order. J. Comput. Appl. Math. 2020, 364, 112301. [Google Scholar] [CrossRef]
- Noeiaghdam, S. Numerical solution of N-th order fredholm integro-differential equations by integral mean value theorem method. Int. J. Pure Appl. Math. 2015, 99. [Google Scholar] [CrossRef] [Green Version]
- Miller, R.K. An integrodifferential equation for rigid heat conductors with memory. J. Math. Anal. Appl. 1978, 66, 313–332. [Google Scholar] [CrossRef] [Green Version]
- Tolstov, G.P. Fourier Series; Dover Publications, Inc.: New York, NY, USA, 1962. [Google Scholar]
- Koh, Y.K.; Cahill, D.G.; Sun, B. Nonlocal theory for heat transport at high frequencies. Phys. Rev. B 2014, 90, 205412. [Google Scholar] [CrossRef]
- Wingert, M.C.; Zheng, J.; Kwon, S.; Chen, R. Thermal transport in amorphous materials: A review. Semicond. Sci. Technol. 2016, 31, 113003. [Google Scholar] [CrossRef]
- Feng, T.; Ruan, X. Prediction of Spectral Phonon Mean Free Path and Thermal Conductivity with Applications to Thermoelectrics and Thermal Management: A Review. J. Nanomater. 2014, 2014, 1–25. [Google Scholar] [CrossRef]
- Stoner, R.J.; Maris, H.J. Kinetic formula for estimating resistive phonon lifetimes. Phys. Rev. B 1993, 47, 11826–11829. [Google Scholar] [CrossRef]
- He, Y.; Donadio, D.; Galli, G. Heat transport in amorphous silicon: Interplay between morphology and disorder. Appl. Phys. Lett. 2011, 98, 144101. [Google Scholar] [CrossRef]
- Zeller, R.C.; Pohl, R.O. Thermal Conductivity and Specific Heat of Noncrystalline Solids. Phys. Rev. B 1971, 4, 2029–2041. [Google Scholar] [CrossRef]
- Choy, C.L.; Tong, K.W.; Wong, H.K.; Leung, W.P. Thermal conductivity of amorphous alloys above room temperature. J. Appl. Phys. 1991, 70, 4919–4925. [Google Scholar] [CrossRef]
- Sørensen, S.S.; Johra, H.; Mauro, J.C.; Bauchy, M.; Smedskjaer, M.M. Boron anomaly in the thermal conductivity of lithium borate glasses. Phys. Rev. Mater. 2019, 3, 075601. [Google Scholar] [CrossRef]
- Sørensen, S.S.; Pedersen, E.J.; Paulsen, F.K.; Adamsen, I.H.; Laursen, J.L.; Christensen, S.; Johra, H.; Jensen, L.R.; Smedskjaer, M.M. Heat conduction in oxide glasses: Balancing diffusons and propagons by network rigidity. Appl. Phys. Lett. 2020, 117, 031901. [Google Scholar] [CrossRef]
- Choy, C. Thermal conductivity of polymers. Polymer 1977, 18, 984–1004. [Google Scholar] [CrossRef]
- Hartwig, G. Polymer Properties at Room and Cryogenic Temperatures; Springer Nature: Berlin/Heidelberg, Germany, 1994. [Google Scholar]
- Landau, L.D.; Lifshitz, E.M. Course of Theoretical Physics 5: Statistical Physics Part 1, 3rd ed.; Pergamon Press: Oxford, UK, 1980. [Google Scholar]
- Landau, L.D.; Lifshitz, E.M. Course of Theoretical Physics 8: Electrodynamics of Continuous Media, 2nd ed.; Butterworth-Heinemann: Oxford, UK, 2000. [Google Scholar]
- Johnston, D.C. Stretched exponential relaxation arising from a continuous sum of exponential decays. Phys. Rev. B 2006, 74, 184430. [Google Scholar] [CrossRef] [Green Version]
- Berberan-Santos, M.; Bodunov, E.; Valeur, B. Mathematical functions for the analysis of luminescence decays with underlying distributions 1. Kohlrausch decay function (stretched exponential). Chem. Phys. 2005, 315, 171–182. [Google Scholar] [CrossRef]
- Anderssen, R.S.; Loy, R.J. Completely monotone fading memory relaxation modulii. Bull. Aust. Math. Soc. 2002, 65, 449–460. [Google Scholar] [CrossRef] [Green Version]
- Schilling, R.L.; Song, R.; Vondraček, Z. Bernstein Functions: Theory and Applications; Hubert: Berlin, Germany, 2010; ISBN 978-3-11-021530-4. [Google Scholar]
- Gupta, P.K.; Moynihan, C.T. Prigogine–Defay ratio for systems with more than one order parameter. J. Chem. Phys. 1976, 65, 4136–4140. [Google Scholar] [CrossRef]
- Tournier, R.F. Formation temperature of ultra-stable glasses and application to ethylbenzene. Chem. Phys. Lett. 2015, 641, 9–13. [Google Scholar] [CrossRef]
- You, K.; Yan, G.; Luo, X.; Gilchrist, M.D.; Fang, F. Advances in laser assisted machining of hard and brittle materials. J. Manuf. Process. 2020, 58, 677–692. [Google Scholar] [CrossRef]
- Sahin, A.Z.; Yilbas, B.; Akhtar, S.S. Laser Surface Treatment and Efficiency Analysis. Compr. Mater. Process. 2014, 9, 307–316. [Google Scholar] [CrossRef]
- Dreglea, A.I.; Sidorov, N.A. Integral equations in identification of external force and heat source density dynamics, Buletinul Academiei de Stiinte a Republicii Moldova. Matematica 2018, 88, 68–77. Available online: http://www.math.md/files/basm/y2018-n3/y2018-n3-(pp68-77).pdf (accessed on 2 February 2021).
- Luo, C.; Sommer, J.-U. Frozen topology: Entanglements control nucleation and crystallization in polymers. Phys. Rev. Lett. 2014, 112, 195702. [Google Scholar] [CrossRef] [PubMed]
- Wyslouzil, B.E.; Seinfeld, J.H. Nonisothermal homogeneous nucleation. J. Chem. Phys. 1992, 97, 2661–2670. [Google Scholar] [CrossRef] [Green Version]
- Mahata, A.; Zaeem, M.A.; Baskes, M.I. Understanding homogeneous nucleation in solidification of aluminum by molecular dynamics simulations. Model. Simul. Mater. Sci. Eng. 2018, 26, 025007. [Google Scholar] [CrossRef]
- Vladimirov, V.S. A Collection of Problems on the Equations of Mathematical Physics; Springer: Berlin/Heidelberg, Germany, 1986; Available online: https://www.springer.com/gp/book/9783662055601 (accessed on 2 February 2021).
- Polyanin, A.D.; Manzhirov, A.V. Handbook of mathematics for engineers and scientists; Chapman & Hall/CRC: Boca Raton, FL, USA; London, UK, 2007. [Google Scholar]
- Korn, G.A.; Korn, T.M. Mathematical Handbook for Scientists and Engineers, 2nd ed; Dover Publications, Inc.: Mineola, NY, USA, 2000. [Google Scholar]







Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Minakov, A.A.; Schick, C. Integro-Differential Equation for the Non-Equilibrium Thermal Response of Glass-Forming Materials: Analytical Solutions. Symmetry 2021, 13, 256. https://doi.org/10.3390/sym13020256
Minakov AA, Schick C. Integro-Differential Equation for the Non-Equilibrium Thermal Response of Glass-Forming Materials: Analytical Solutions. Symmetry. 2021; 13(2):256. https://doi.org/10.3390/sym13020256
Chicago/Turabian StyleMinakov, Alexander A., and Christoph Schick. 2021. "Integro-Differential Equation for the Non-Equilibrium Thermal Response of Glass-Forming Materials: Analytical Solutions" Symmetry 13, no. 2: 256. https://doi.org/10.3390/sym13020256