Numerical Simulation and Mathematical Modeling of Electro-Osmotic Couette–Poiseuille Flow of MHD Power-Law Nanofluid with Entropy Generation

Abstract

The basic motivation of this investigation is to develop an innovative mathematical model for electro-osmotic flow of Couette–Poiseuille nanofluids. The power-law model is treated as the base fluid suspended with nano-sized particles of aluminum oxide (Al₂O₃). The uniform speed of the upper wall in the axial path generates flow, whereas the lower wall is kept fixed. An analytic solution for nonlinear flow dynamics is obtained. The ramifications of entropy generation, magnetic field, and a constant pressure gradient are appraised. Moreover, the physical features of most noteworthy substantial factors such as the electro-osmotic parameter, magnetic parameter, power law fluid parameter, skin friction, Nusselt number, Brinkman number, volume fraction, and concentration are adequately delineated through various graphs and tables. The convergence analysis of the obtained solutions has been discussed explicitly. Recurrence formulae in each case are also presented.

1. Introduction

Conventional fluids like glycol, acetone, kerosene and water have low heat transfer characteristics and play an important role in laboratories and industrial engineering applications. Several experiments and procedures have been demonstrated to improve heat transfer characteristics. A significant contribution of boosting the heat transfer ability of fluids in an industrial process by the insertion of nanoparticles into the fluids was found. The pioneering work of Choi [1] led to the discovery that heat transfer rate and higher thermal conductivity can be enriched by a combination of base fluids and nanoparticles. Later, Xuan [2] experimentally investigated the enrichment of thermal conductivity in nanofluids. Some core developments have been collated in references [3,4,5,6,7,8,9].

Further, power-law fluids have attracted the attention of many scientists as the description of power-law fluids happens to be the best description of fluid behavior (with right choice of power-law index) of shear-dependent fluids. There are several more models that better describe the range of shear rates, but they do so at the cost of simplicity. For this reason, the power law is used to describe fluid behavior as compared to other fluid models. Recently, Ouyang et al. [10] proposed a two-dimensional squirmer model for power law fluids. They concluded that the selection of power law relation is the best choice to demonstrate the rheological properties of three sorts of fluids, namely: (i) Newtonian, (ii) shear-thickening, and (iii) shear-thinning fluids. Also, the exact velocity at the bottom region of shear rate cannot augur the basis of the power law model. After overcoming the insufficiency of power law, it cannot be used to find the exact velocity profile for the shear rate of the bottom and zero regions [11]. Also, power law fluid in some cases is used to describe non-Newtonian fluids [12,13]

Electro-osmotic flow, also known as electro-osmosis flow, is used in microfluidic devices and electronically controlled fluid flow or any other fluid conduit. Zhao et al. [14] have invoked electro-osmotic flow in a channel with the power law model. Das and Chakraborty [15] investigated the impact of non-Newtonian fluid on electro-osmotic flow. Several attempts regarding electro-osmosis flow can be found in references [16,17,18,19].

It is well known that magnetic fluids have significant utilization in applications such as heat transfer, cancer therapy, opto-electronic devices, sensors, cooling of nuclear reactors, liquid metal flow control, high temperature plasmas, solidification of binary alloys, drying processes etc. [20,21,22,23,24,25]. In addition, a number of researchers have conducted promising investigations on nanoparticles. Examples include the work of Malvandi et al. [26] who have studied MHD mixed convection with nanoparticle migration and Yousif et al. [27] who publicized magnetohydrodynamics (MHD) Carreau nanofluids with internal heat source/sink radiation. Further, magnetic nanofluids also exhibit interesting properties that are used in various microfluidic applications, dipolar nanoparticles, magnetic fluid hyperthermia and magnetic resonance imaging [28,29,30,31]. The existing literature bears witness that magnetic fluids with nanoparticles exhibit several interesting structural characteristics depending on the applied magnetic field strength. As a result, several studies have also been undertaken on MHD rheological fluids [32,33,34].

In recent years, prominent authors have been inspired to study entropy generation by various applications, such as diffusion and Joule heating. Entropy is caused by irreversible processes of a system and can be reduced only when it interacts with some other system whose entropy increases in the process. Bejan [35] studied the entropy generation for a flow system and discussed the main ideas to control the energy loss in flow problems and enhanced the ability of the system. Zeeshan et al. [36] discussed the radiative and electro-magnetohydrodynamic effects of a titanium dioxide/water based nanofluid on entropy generation. Ranjit and Shit [37] presented the effects of entropy generation with MHD on electro-osmotic flow. Numerical analysis for entropy generation on nanofluids with the suspension of nanoparticles (such as copper, Al₂O₃ and TiO₃) in water as a base fluid, which passes through wavy walls, was conducted by Cho et al. [38]. Different researchers have devoted their efforts to explore the impact of entropy generation to real world problems [39,40,41,42,43].

Thus far, the simultaneous effects of entropy generation, MHD and electro-osmosis on power law nanofluid flow has not been studied. In order to fill this gap, the next section is devoted to developing a mathematical formulation of the problem, which comprises mass, momentum, and energy equations. The situation becomes difficult as the resulting equations are not only nonlinear, but also coupled. The analytical findings are developed by a homotopic tactic [44] that has been used effectively for the last two decades [45,46,47,48,49,50].

The acquired results satisfied the governing equations and boundary conditions. The physical features involve parameters which are adequately determined through various graphs and tables.

2. Problem Design

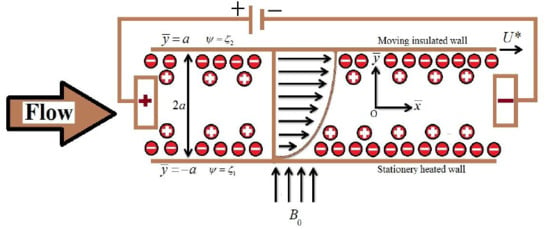
2.1. Physical Considerations

Incompressible and steady nanofluids pass through horizontal parallel plates as illustrated in Figure 1. The wall at $\overline{y}=a$ moves with constant velocity $U^{\ast }$ while the second wall remains stationary at $\overline{y}=-a.$ $B_0$ is uniform transverse magnetic field, ${\xi }_1$ is zeta potential at lower wall, ${\xi }_2$ is zeta potential at upper wall, $\psi$ is electric double layer potential and $2a$ is the total width of the channel.

2.2. Electrical Potential Distribution

During the process of electro-osmotic flow (EOF), the separation of ions takes place and an electrical double layer (EDL) forms adjacent to the channel walls, thereby developing electric potential distribution. The electric potential $\overline{\psi }$ within the channel, described by the Poisson–Boltzmann equation [51] in the Cartesian co-ordinate system, can be calculated as:

$$\frac{{\partial }^2\overline{\psi }}{\partial {\overline{x}}^2}+\frac{{\partial }^2\overline{\psi }}{\partial {\overline{y}}^2}=-\frac{{\overline{\rho }}_e\left(\overline{y}\right)}{\epsilon }$$

(1)

For small values of electrical potential $\overline{\psi }$ of the EDL, the Debye–Hückel approximation can be applied and Equation (1) becomes:

$${\nabla }^2\overline{\psi }={\overline{\kappa }}^2\overline{\psi },{\overline{\kappa }}^2=\frac{2n_0{z_v}^2{e}^2}{\epsilon k_B\widehat{T}}.$$

(2)

The plates of the channel are made of different materials and have different zeta potentials.

$$\overline{\psi }={\zeta }_1\mathrm{at}\overline{y}=-a\mathrm{and}\overline{\psi }={\zeta }_2\mathrm{at}\overline{y}=a.$$

(3)

The electrical potential under the action of Equation (3) can be explored as:

$$\overline{\psi }(\overline{y})=\frac{{\zeta }_1\mathrm{Sinh}\left(\overline{\kappa }\left(a-\overline{y}\right)\right)+{\zeta }_2\mathrm{Sinh}\left(\overline{\kappa }\left(a+\overline{y}\right)\right)}{\mathrm{Sin}\left(2a\overline{\kappa }\right)}$$

(4)

The electric double layer effects are produced by the external field relation $\mathbf{E}=(E_x,0,0)$ and charge density of nanoparticles. The external electric force ${\overline{\rho }}_e\mathbf{E}$, also called the electro-kinetic force [52,53], is generated outside of the charge particle. Along with ${\overline{\rho }}_e\left(\overline{y}\right)$, electric charge density is defined as:

$${\overline{\rho }}_e(\overline{y})=-\epsilon {\overline{\kappa }}^2\left(\frac{{\zeta }_1\mathrm{Sinh}\left(\overline{\kappa }\left(a-\overline{y}\right)\right)+{\zeta }_2\mathrm{Sinh}\left(\overline{\kappa }\left(a+\overline{y}\right)\right)}{\mathrm{Sin}\left(2a\overline{\kappa }\right)}\right)$$

(5)

where $\epsilon$, $\overline{\kappa }$, $n_0$, $z_v$, $e$, $k_B$ and $\widehat{T}$ are the relative permittivity of the medium, Debye parameter, ion density of bulk liquid, valence of ions, electron charge, Boltzmann constant and absolute temperature, respectively.

2.3. Power Law Model

In the current study, the following power law fluid model [54] is used:

$$\tau ={\mu }_{nf}{\left(\frac{\partial \overline{u}}{\partial \overline{y}}\right)}^{n-1}\left(\frac{\partial \overline{u}}{\partial \overline{y}}\right)=\{\begin{array}{ll}{\mu }_{nf}{\left(\frac{\partial \overline{u}}{\partial \overline{y}}\right)}^n& \mathrm{for}\frac{\partial \overline{u}}{\partial \overline{y}}>0\\ -{\mu }_{nf}{\left(-\frac{\partial \overline{u}}{\partial \overline{y}}\right)}^n& \mathrm{for}\frac{\partial \overline{u}}{\partial \overline{y}}<0.\end{array}$$

(6)

where $\tau$ is shear stresses, $n$ is the power-law or flow behavior index of the fluid and ${\mu }_{nf}$ is the viscosity of the nanofluid [55] and is defined along the consistency index $\delta$ as:

$${\mu }_{nf}=\left(123{\varphi }^2+7.3\varphi +1\right){\mu }_f$$

(7)

and the viscosity of the base fluid in the current discussion is taken as:

$${\mu }_f=\delta {\left(\frac{\partial \overline{u}}{\partial \overline{y}}\right)}^{n-1}.$$

(8)

One signifies a Newtonian fluid for $n=1$ whereas $n<1$ and $n>1$ respectively denote the shear-thinning and shear-thickening of fluids.

To estimate the shear stresses of a fluid, we will illustrate further investigations with shear-thinning properties. Thus, shear stress for the non-Newtonian power-law model can be written as:

$$\tau =\delta \left(123{\varphi }^2+7.3\varphi +1\right)\left(\frac{\partial \overline{u}}{\partial \overline{y}}\right){\left(\frac{\partial \overline{u}}{\partial \overline{y}}\right)}^{n-1}.$$

(9)

2.4. Governing Equations

The electro-osmotic flow occurs in the channel due to the movement of an upper wall, whereas the flow around the channel of the walls is generated because of an applied electric field. The governing equations for the current flow phenomenon are:

$$\mathbf{\nabla }.\mathbf{V}=0$$

(10)

$$\left(\mathbf{V}.\mathbf{\nabla }\right)\mathbf{V}=\frac{1}{{\rho }_{nf}}\left(-\mathbf{\nabla }\overline{p}+\mathbf{\nabla }.\tau +Bodyforce\right)$$

(11)

$$\left(\mathbf{V}.\mathbf{\nabla }\right)T={\alpha }_{nf}{\nabla }^{2}T+\frac{1}{{\left(\rho C_p\right)}_{nf}{\sigma }_{nf}}{\mathbf{J}}^2+\frac{1}{{\left(\rho C_p\right)}_{nf}}\Gamma$$

(12)

where $\mathbf{V}$, $T$ and $\Gamma$ correspondingly represent velocity, temperature and viscous dissipation. The body force contains magnetic, electrical and buoyancy effects.

$$Bodyforce=\underset{\mathrm{Lorentz}\mathrm{force}}{\underbrace{\left(\mathbf{J}\times \mathbf{B}\right)}}+\underset{\mathrm{External}\mathrm{Electric}\mathrm{force}}{\underbrace{{\overline{\rho }}_e\mathbf{E}}}+\underset{\mathrm{Buoyancy}\mathrm{force}}{\underbrace{{\left(\rho \beta \right)}_{nf}\mathbf{g}\left(T-T_w\right)}}$$

(13)

and

$$\Gamma ={\mu }_{nf}{\left(\frac{\partial \overline{u}}{\partial \overline{y}}\right)}^2.$$

(14)

Under the application of Lorentz force, it produces the following Joules heating effects.

$$\frac{1}{{\sigma }_{nf}}{\mathbf{J}}^2={\sigma }_{nf}{B_0}^2{\overline{u}}^2\mathrm{and}\mathbf{J}\times \mathbf{B}=\left(-{\sigma }_{nf}{B}_0\overline{u},0,0\right)$$

(15)

The governing Equations (10) and (12) in components form after omitting the axial heat conductions at the walls and in the fluid [54] and become:

$$\frac{\partial \overline{p}}{\partial \overline{x}}={\mu }_{nf}\frac{{\partial }^2\overline{u}}{\partial {\overline{y}}^2}-{\sigma }_{nf}{B_0}^2\overline{u}+{\left(\rho \beta \right)}_{nf}\left(T-T_w\right)g+{\overline{\rho }}_e\left(\overline{y}\right)E_x$$

(16)

$$\overline{u}\frac{\partial T}{\partial \overline{x}}={\alpha }_{nf}\frac{{\partial }^{2}T}{\partial {\overline{y}}^2}+\frac{{\sigma }_{nf}{B_0}^2}{{\left(\rho C_p\right)}_{nf}}{\overline{u}}^2+\frac{{\mu }_{nf}}{{\left(\rho C_p\right)}_{nf}}{\left(\frac{\partial \overline{u}}{\partial \overline{y}}\right)}^2.$$

(17)

The associated boundary conditions are:

$$\begin{array}{l}\left(\mathrm{At}\mathrm{upper}\mathrm{wall}\right):\overline{u}=U^{\ast },k_f\frac{\partial T}{\partial \overline{y}}=0\mathrm{at}\overline{y}=a\\ \left(\mathrm{At}\mathrm{lower}\mathrm{wall}\right):\overline{u}=0,-k_f\frac{\partial T}{\partial \overline{y}}=q_w\mathrm{at}\overline{y}=-a\end{array}\}$$

(18)

The effective density, heat capability, and thermal and electrical conductivities of a nanofluid [55] are respectively given by:

$$\frac{{\rho }_{nf}}{{\rho }_p}=\left[\left(1-\varphi \right)\frac{{\rho }_f}{{\rho }_p}+\varphi \right]$$

(19)

$$\frac{{\left(\rho C_p\right)}_{nf}}{{\left(\rho C_p\right)}_p}=\left[\left(1-\varphi \right)\frac{{\left(\rho C_p\right)}_f}{{\left(\rho C_p\right)}_p}+\varphi \right]$$

(20)

$$\frac{k_{nf}}{k_f}=\left(4.97{\varphi }^2+2.72\varphi +1\right)$$

(21)

$$\frac{{\sigma }_{nf}}{{\sigma }_f}=\left[1+\frac{3\left(\frac{{\sigma }_p}{{\sigma }_f}-1\right)\varphi }{\left(\frac{{\sigma }_p}{{\sigma }_f}+2\right)-\left(\frac{{\sigma }_p}{{\sigma }_f}-1\right)\varphi }\right].$$

(22)

The following dimensionless transformations

$$\begin{array}{l}\overline{y}=ay,\overline{u}=u_{m}u,U^{\ast }=u_{m}U,\overline{p}={\rho }_f{u_m}^{2}p{\left(a/u_m\right)}^n,\theta =\frac{T-T_w}{q_{w}a/k_f},\\ {\overline{\rho }}_e=-\left(\epsilon {\zeta }_1/a^2\right){\rho }_e,\overline{\kappa }=\kappa /a,\psi =\overline{\psi }/{\zeta }_1\end{array}\},$$

(23)

Transform Equations (16) and (17) by using (23) in the dimensionless form as:

$$\left(123{\varphi }^2+7.3\varphi +1\right)n{\left(\frac{\partial u}{\partial y}\right)}^{n-1}\frac{{\partial }^{2}u}{\partial y^2}-A_4{M}^{2}u+A_{3}Gr\theta +{\beta }_u{\rho }_e-ReP=0,$$

(24)

$$\left(4.97{\varphi }^2+2.72\varphi +1\right)\frac{{\partial }^2\theta }{\partial y^2}+Br\left(123{\varphi }^2+7.3\varphi +1\right){\left(\frac{\partial u}{\partial y}\right)}^{n+1}-B_1\gamma u{A}_4+Br{M}^2{u}^2=0.$$

(25)

$$\begin{array}{lllll}u=U,& \frac{\partial \theta }{\partial y}=0& \mathrm{at}& y=1& \left(\mathrm{Upper}\mathrm{wall}\right)\\ u=0,& \frac{\partial \theta }{\partial y}=-1& \mathrm{at}& y=-1& \left(\mathrm{Lower}\mathrm{wall}\right)\end{array}\}.$$

(26)

In which

$$\begin{array}{l}Gr=\frac{{\left(\rho \beta \right)}_{f}g{q}_w{a}^3}{\delta k_f{u}_m}{\left(\frac{a}{u_m}\right)}^{n-1},Re=\frac{{\rho }_f{u}_{m}a}{\delta }{\left(\frac{a}{u_m}\right)}^{n-1},M^2=\frac{{\sigma }_f{B_0}^2{a}^2}{\delta }{\left(\frac{a}{u_m}\right)}^{n-1}\\ Br=\frac{\delta {u_m}^2}{q_{w}a}{\left(\frac{a}{u_m}\right)}^{1-n},U_{Hs}=-\frac{\epsilon {\zeta }_1{E}_x}{\delta }{\left(\frac{a}{u_m}\right)}^{n-1},{\beta }_u=\frac{U_{Hs}}{u_m},\gamma =\frac{k_f{u}_{m}a}{{\alpha }_f{q}_w}\frac{\partial T}{\partial x},\\ {\rho }_e(y)={\kappa }^2\left(\frac{\mathrm{Sinh}\left(\kappa \left(1-y\right)\right)+R_{\zeta }\mathrm{Sinh}\left(\kappa \left(1+y\right)\right)}{\mathrm{Sin}\left(2\kappa \right)}\right),{\alpha }_f=\frac{{\left(\rho C_p\right)}_f}{k_f}\\ A_4=\frac{{\sigma }_{nf}}{{\sigma }_f},A_3=\frac{{\left(\rho \beta \right)}_{nf}}{{\left(\rho \beta \right)}_f},B_1=\frac{{\left(\rho C_p\right)}_{nf}}{{\left(\rho C_p\right)}_f},R_{\zeta }={\zeta }_2/{\zeta }_1.\end{array}\}.$$

(27)

where $\kappa$ is the electro-osmotic parameter, $\rho$ is density, $\mu$ is dynamic viscosity, $\beta$ is volumetric volume expansion, $Gr$ is Grashof number and $C_p$ is specific heat. Assume that $u_m=-\left(a^2/2{\mu }_f\right)\partial p/\partial \overline{x}$ is the maximum velocity between two plates, and ${\beta }_u$ is the ratio between electro-osmotic velocity $U_{Hs}$ and maximum velocity of the fluid. Thermophysical properties of alumina and the base fluid polyvinyl chloride (PVC) are illustrated below in

Table 1. Physical properties of PVC [56] and Al₂O₃ [52].

Properties		${\mathit{C}}_{\mathit{p}}$ (J kg−1 K−1)	$\mathit{\beta }\times {10}^{-5}$ (K−1)	$\mathit{\rho }$ (kg m−3)	$\mathit{k}$ (W m−1 K−1)	$\mathit{\mu }$ (Ns m−2)
Al2O3		765	8.5 × 10−1	3970	40	-----
PVC	2%	4117.56	21.9	1006.24	0.586	0.0015
	3%	4085.34	21.8	1010.25	0.579	0.00107
	4%	4053.12	21.8	1014.27	0.572	0.00114
	5%	4020.9	21.8	1018.29	0.718	0.00114
	6%	3988.68	21.8	1022.31	0.559	0.00116
	7%	3956.46	21.7	1026.33	0.552	0.00119

.

2.5. Thermophysical Relations

Skin friction is defined as:

$$C_f=\frac{2{\tau }_w}{{\rho }_f{u}_m^2}\mathrm{and}{\tau }_w=\delta \left(123{\varphi }^2+7.3\varphi +1\right)\left(\frac{\partial \overline{u}}{\partial \overline{y}}\right){\left(\frac{\partial \overline{u}}{\partial \overline{y}}\right)}^{n-1};\overline{y}=\pm a$$

(28)

Moreover, in the present study, different concentration of alumina particles (Al₂O₃) are used in the polymer solution of polyvinyl alcohol in water; consequently, different values of $\tau$ in correlation with nanoparticle volume fraction $\varphi$ for different concentrations of polyvinyl alcohol are listed in

Table 2. Properties of the power-law equation and PVC solutions [56].

PVC (%)	Consistency Index $\mathit{\delta }$	Power Index $\mathit{n}$	Shear Stress
2	0.00494	0.790	$\tau =0.00494\left(123{\varphi }^2+7.3\varphi +1\right){\left(\partial \overline{u}/\partial \overline{y}\right)}^{0.790}$
3	0.00925	0.764	$\tau =0.00925\left(123{\varphi }^2+7.3\varphi +1\right){\left(\partial \overline{u}/\partial \overline{y}\right)}^{0.764}$
4	0.01557	0.734	$\tau =0.01557\left(123{\varphi }^2+7.3\varphi +1\right){\left(\partial \overline{u}/\partial \overline{y}\right)}^{0.734}$
5	0.02170	0.718	$\tau =0.02170\left(123{\varphi }^2+7.3\varphi +1\right){\left(\partial \overline{u}/\partial \overline{y}\right)}^{0.718}$
6	0.02616	0.691	$\tau =0.02616\left(123{\varphi }^2+7.3\varphi +1\right){\left(\partial \overline{u}/\partial \overline{y}\right)}^{0.691}$
7	0.03033	0.663	$\tau =0.03033\left(123{\varphi }^2+7.3\varphi +1\right){\left(\partial \overline{u}/\partial \overline{y}\right)}^{0.663}$

.

Hence, the coefficient of skin friction in the dimensionless form for both walls is:

$$C_f=\frac{2}{Re}\left(123{\varphi }^2+7.3\varphi +1\right){\left(\frac{\partial u}{\partial y}\right)}^n\mathrm{at}y=\pm 1.$$

(29)

2.6. Heat Transfer Rate

The Nusselt number is defined as:

$$Nu=\frac{ah}{k_f}\mathrm{and}h=\frac{q_w}{T_w-T_m}$$

(30)

Here, $h$ is heat transfer coefficient, $q_w$ is wall heat flux and $T_m$ is bulk mean temperature, which is given by:

$$T_m=\frac{{\displaystyle \int {\rho }_f\overline{u}TdA}}{{\displaystyle \int {\rho }_f\overline{u}dA}}.$$

(31)

The mean temperature in the dimensionless form becomes:

$${\theta }_m=\frac{k_f\left(T_m-T_w\right)}{q_{w}a}.$$

(32)

Therefore, the Nusselt number is:

$$Nu=-\frac{1}{{\theta }_m}.$$

(33)

2.7. Entropy Generation

The entropy generation of local volumetric rate can be defined as:

$$S_G=\frac{k_{nf}}{T_w^2}{\left(\frac{\partial \overline{T}}{\partial \overline{y}}\right)}^2+\frac{{\mu }_{nf}}{T_w}{\left(\frac{\partial \overline{u}}{\partial \overline{y}}\right)}^2+\frac{{\sigma }_{nf}{B}_0^2{\overline{u}}^2}{T_w}+\frac{{\rho }_e\left(\overline{y}\right)E_x}{T_w}.$$

(34)

The characteristic entropy generation can be expressed as:

$$S_0=\frac{q_w^2}{k_f{T}_w^2},$$

(35)

By using the transformation given in Equation (23), the non-dimensional total entropy generation may be expressed as:

$$Ns=\frac{S_G}{S_0}=\left(4.97{\varphi }^2+2.72\varphi +1\right){\left(\frac{\partial \theta }{\partial y}\right)}^2+\frac{Br}{\Omega }\left(\left(123{\varphi }^2+7.3\varphi +1\right){\left(\frac{\partial u}{\partial y}\right)}^{n+1}+A_4{M}^2{u}^2+{\beta }_u{\rho }_{e}u\right),$$

(36)

where $M,$ $Br,$ ${\beta }_u$, ${\rho }_e$ and $\Omega$ are respectively the magnetic field, Brinkman number, volumetric volume expansion, dimensional electric charge density, and dimensionless temperature difference. These parameters are defined as:

$$\begin{array}{l}{M}^2=\frac{{\sigma }_f{B}_0^2{a}^2}{K}{\left(\frac{a}{u_m}\right)}^{n-1},Br=\frac{K{u}_m^2}{q_{w}a}{\left(\frac{a}{u_m}\right)}^{1-n},{\beta }_u=\frac{U_{Hs}}{u_m},\\ {\rho }_e=-(\epsilon {\zeta }_1/a^2){\rho }_e,\Omega =\frac{q_{w}a}{k_f{T}_w}\end{array}\}.$$

(37)

$$Be=\frac{\mathrm{Entropy}\mathrm{due}\mathrm{to}\mathrm{heat}\mathrm{transfer}}{\mathrm{Total}\mathrm{entropy}\mathrm{geeration}}$$

(38)

$$Be=\frac{\left(4.97{\varphi }^2+2.72\varphi +1\right){\left(\frac{\partial \theta }{\partial y}\right)}^2}{\left(4.97{\varphi }^2+2.72\varphi +1\right){\left(\frac{\partial \theta }{\partial y}\right)}^2+\frac{Br}{\Omega }\left(\left(123{\varphi }^2+7.3\varphi +1\right){\left(\frac{\partial u}{\partial y}\right)}^{n+1}+A_4{M}^2{u}^2+{\beta }_u{\rho }_{e}u\right)},$$

(39)

3. Discussion of Results

3.1. Analytic Solution

In this section, we intend to find the analytical solutions by means of the homotopy analysis method [57]. We chose the initial guesses $u_0$, ${\theta }_0$ and linear operators ${\pounds }_1,{\pounds }_2$, [58] as:

$$u_0\left(y\right)=\frac{1}{2}\left(1+y\right)U,{\theta }_0\left(y\right)=\frac{1}{4}y\left(y-2\right).$$

(40)

$${\pounds }_1=\frac{d}{dy}\left(\frac{du}{dy}\right),{\pounds }_2=\frac{d}{dy}\left(\frac{d\theta }{dy}\right).$$

(41)

The deformation equations of homotopy for the zeroth-order are established as:

$$\begin{array}{l}\left(1-\xi \right){\pounds }_1\left[\theta \left(y,\hspace{0.17em}\xi \right)-{\theta }_0\left(y\right)\right]=\xi {\hslash }_u{N}_1\left[u\left(y,\hspace{0.17em}\xi \right),\hspace{0.17em}\theta \left(y,\hspace{0.17em}\xi \right)\right],\\ \left(1-\xi \right){\pounds }_2\left[\theta \left(y,\hspace{0.17em}\xi \right)-{\theta }_0\left(y\right)\right]=\xi {\hslash }_{\theta }{N}_2\left[u\left(y,\hspace{0.17em}\xi \right),\hspace{0.17em}\theta \left(y,\hspace{0.17em}\xi \right)\right]\end{array}\}$$

(42)

$$\begin{array}{lll}\mathrm{For}& \xi =0& \xi =1\\ u\left(y,\xi \right):& u_0\left(y\right)& u\left(y\right)\\ \theta \left(y,\hspace{0.17em}\xi \right):& {\theta }_0\left(y\right)& \theta \left(y\right)\end{array}\}$$

(43)

The nonlinear operators $N_1$, $N_2$ are can be written as:

$$\begin{array}{ll}{N}_1\left[u\left(y,\hspace{0.17em}\xi \right),\hspace{0.17em}\theta \left(y,\hspace{0.17em}\xi \right)\right]=& \left(123{\varphi }^2+7.3\varphi +1\right)n{\left(\frac{\partial u\left(y,\hspace{0.17em}\xi \right)}{\partial y}\right)}^{n-1}\frac{{\partial }^{2}u\left(y,\hspace{0.17em}\xi \right)}{\partial y^2}-A_4{M}^{2}u\left(y,\hspace{0.17em}\xi \right)+\\ & A_{3}Gr\theta \left(y,\hspace{0.17em}\xi \right)+{\beta }_u{\rho }_e-ReP,\\ N_2\left[u\left(y,\hspace{0.17em}\xi \right),\hspace{0.17em}\theta \left(y,\hspace{0.17em}\xi \right)\right]=& \left(4.97{\varphi }^2+2.72\varphi +1\right)\frac{{\partial }^2\theta \left(y,\hspace{0.17em}\xi \right)}{\partial y^2}+A_{4}Br{M}^2{\left(u\left(y,\hspace{0.17em}\xi \right)\right)}^2+\\ & Br\left(123{\varphi }^2+7.3\varphi +1\right){\left(\frac{\partial u\left(y,\hspace{0.17em}\xi \right)}{\partial y}\right)}^{n+1}-B_1\gamma u\left(y,\hspace{0.17em}\xi \right)\end{array}\}.$$

(44)

The solution for velocity and temperature up to $mth$-order approximation can be expressed as:

$$u\left(y\right)=u_0\left(y\right)+{\displaystyle \sum }_{l=1}^m{u}_l\left(y\right)\hspace{0.17em},\theta \left(y\right)={\theta }_0\left(y\right)+{\displaystyle \sum }_{l=1}^m{\theta }_l\left(y\right).$$

(45)

The best solutions for solving coupled differential equation can be presented as below at 20th order approximations:

$$u(y)=C_1+C_{2}y+C_3{y}^2+C_4{y}^3+C_5{y}^4+C_6{y}^5+C_7{y}^6+C_8{y}^7$$

(46)

$$\theta (y)=D_1+D_{2}y+D_3{y}^2+D_4{y}^3+D_5{y}^4+D_6{y}^5$$

(47)

The constants $C_1$ to $C_8$ and $D_1$ to $D_6$ are specified in Appendix A.

3.2. Convergence Inspection

As pointed out by Liao [59], the convergence of homotopic results can be controlled by the auxiliary parameters ${\hslash }_u$ and ${\hslash }_{\theta }$. In Figure 2 and Figure 3, it is observed that the minimum error for the velocity and temperature profiles can be achieved at ${\hslash }_u=-0.5$ and ${\hslash }_{\theta }=-0.65$.

In addition, the residual error norms have been utilized to further ensure the accuracy of the obtained series solutions. The residual errors of the velocity and temperature profiles for two succeeding approximations of temperature $E_{\theta }$ and velocity $E_u$ up to the 20th order iteration as given in

Table 3. Residual error of series solutions when $Gr=3.1556$, $Br=1$, $Re=442.956$, $\beta =1$, $M=0.1$ and $\rho e=1$.

Order of Approximation	Time	${\mathit{E}}_{\mathit{u}}$	${\mathit{E}}_{\mathit{\theta }}$
05	8.2651	9.8020 × 10−3	9.8561 × 10−3
10	29.3761	9.3023 × 10−3	7.6511 × 10−3
15	62.4216	2.3452 × 10−3	2.2438 × 10−3
20	100.0125	1.0411 × 10−3	1.9624 × 10−3

can be obtained by the following expressions:

$$E_u=\sqrt{\frac{1}{21}{\displaystyle \sum _{i=0}^{20}{\left(u\left(i/20\right)\right)}^2}}\mathrm{and}{E}_{\theta }=\sqrt{\frac{1}{21}{\displaystyle \sum _{j=0}^{20}{\left(\theta \left(j/20\right)\right)}^2}}.$$

(48)

3.3. Graphical Illustration

The current research is about flow and entropy on a magnetized power law nanofluid along the horizontal walls. The effects of the nanofluid can be determined at the same pressure with the electric body force and the motion of the upper plate. Flow and entropy generation on the magnetized power law of a nanofluid in the horizontal channel are studied systematically. The lower wall is heated, and the upper wall maintains the temperature. The influence of different important parameters such as Grashof number, electro-osmosis, Reynolds number, magnetic field, Brinkman number, entropy generation, nanoparticle volume fraction and Bejan number on temperature and velocity distributions were illustrated graphically in Figure 4, Figure 5, Figure 6, Figure 7, Figure 8, Figure 9, Figure 10, Figure 11, Figure 12, Figure 13, Figure 14, Figure 15, Figure 16, Figure 17, Figure 18, Figure 19, Figure 20, Figure 21, Figure 22 and Figure 23. By using different parameters, we get different results which can be explained as $n=0.764$ $\left(\mathrm{PVC}3\%\right)$, $\varphi =0.03$, $M=2$, ${\beta }_u=0.3$, $\gamma =10$, $\kappa =8$, $Gr=2.366$, $Re=442.956$ and $Br=1$.

The impact of $M$ on temperature and velocity is demonstrated in Figure 4 and Figure 5. They show that when the magnetic parameter increases, the velocity profile decreases while the temperature profile increases. When one applies a magnetic field on electrically treated nanofluid, then it produces a force opposite to the flow direction. Consequently, the Lorentz force increases the magnetic parameter which opposes the fluid flow, and due to that, the velocity distribution decreases and the temperature distribution upsurges. The effects of volume fraction $\varphi$ on temperature are depicted in Figure 6. The temperature profile increases by increasing the $\varphi$ volume fraction. Various concentrations of polyvinylchloride (PVC) on temperature and velocity are illustrated in Figure 7 and Figure 8. From Figure 7, it is observed that the velocity distribution rises with the increase of PVC. The temperature for various values of PVC are portrayed in Figure 8. It can be seen that temperature is a decreasing function between the channel. Figure 9 shows the effect of ${\beta }_u$ on velocity profile. ${\beta }_u$ can be expressed as the ratio of $U_{Hs}$ and $u_m$ of a nanofluid. Figure 9 shows that flow of a channel exceeds and gains its high value. Figure 10 reveals a minute change for increasing values of the electro-osmotic parameter for velocity and temperature. The effects of the electro-osmotic value of $\kappa$ on temperature and velocity profile are shown in Figure 11 and Figure 12. It can be seen from Figure 11 that by increasing $\kappa$, the velocity profile increases. This is due to a larger value of $\kappa$ for the velocity profiles that display EDL layers. The effect of electro-osmotic $\kappa$ on temperature is illustrated in Figure 12, which gives the deficiency of the Joule effect. It is also noted that if the pseudo-plastic increases in electro-osmotic parameter $\kappa$, it results in a notable increase in temperature. The effect of $Br$ on temperature is shown in Figure 13. It is perceived that by increasing $Br$, the temperature decreases, from which we conclude that $Br$ increases as compared to bulk mean temperature. The effect of Brinkman number with respect to volume friction is expressed in Figure 14. It is perceived that for a developing Brinkman number with respect to volume fraction, the Nusselt number increases. Results indicate that temperature increases for higher values of nanoparticle volume fraction. The influence of $U_{Hs}$ and $u_m$ of nanofluid ${\beta }_u$ and $\kappa$ on the Nusselt number are shown in Figure 15. It is seen that near the heated wall, the Nusselt number reduces; this is because first heat is moved to the fluid and then transferred into a separated plate.

The entropy generation profiles for various important parameters such as volumetric volume expansion $\beta$, magnetic field $M$, dimensionless temperature parameter $Br{\Omega }^{-1}$, and Brinkman number $Br$ are illustrated in Figure 16, Figure 17, Figure 18, Figure 19, Figure 20 and Figure 21. The impact of $M$ on entropy generation is displayed in Figure 16. It can be observed that when M increases, the entropy generation decreases on the left side with minimum energy loss at $y=-0.25$; after this, increasing behavior is detected. The effect of $\beta$ on entropy generation is depicted in Figure 17, where it can be observed that when $\beta$ is increasing, the entropy generation is also increased. The energy loss on the upper wall is comparatively greater when compared to the lower wall. The significance of $Br$ on entropy generation in Figure 18 shows that when $Br$ increases, entropy generation decreases on the left side and has minimum energy loss at y = 0; after this, an increasing trend on the left side is seen. The influence of $Br{\Omega }^{-1}$ on entropy generation is given in Figure 19 and it is observed that entropy generation decreases on the lower wall and has minimum energy loss at $y=0.15$. Figure 20 shows that when the electro-osmotic parameter increases, entropy generation also increases. From Figure 21, it is observed that when $R_{\zeta }$ increases, the entropy generation at the lower wall decreases, but after $y=0$, it increases at the upper wall. Figure 22 shows that when the magnetic parameter increases, Bejan number also increases. It is observed that there is a dominant effect on the lower as well as the upper wall. Figure 23 shows that when $Br{\Omega }^{-1}$ increases, the Bejan number also increases. It is noted that the Bejan number shows a dominant role on the upper wall.

The impact of the different parameters on skin friction such as the electro-osmotic parameter, the ratio between $U_{Hs}$ and $u_m$, volume concentration, Brinkman number, and magnetic field are given in

Table 4. Coefficient of skin friction $C_f$ with $M$, $Br$ and ${\beta }_u$ along $n=0.764$ $\left(\mathrm{PVC}3\%\right)$.

$\mathit{\beta }$	$\mathit{M}$	$\mathit{B}\mathit{r}$	${\mathit{C}}_{\mathit{f}-\mathit{h}1}$	${\mathit{C}}_{\mathit{f}-\mathit{h}2}$
0.1	0.1	0.0	0.00317506	0.00388072
0.2			0.00317497	0.00388079
0.3			0.00317489	0.00388087
0.4			0.00317481	0.00388095
	0.0		0.00317423	0.00388169
	0.5		0.00317428	0.00388157
	1.0		0.00317443	0.00388152
	1.5		0.00317468	0.00388148
		0.0	0.00317506	0.00388072
		1.0	0.00317512	0.00388066
		2.0	0.00317518	0.00388060
		3.0	0.00317524	0.00388054

. It is found that by increasing the Brinkman number and the magnetic parameter, the skin friction decreases.

4. Conclusions

In this work, the effects of entropy generation on power law nanofluid through a horizontal channel in a way that one wall is movable and the other is stationary are presented. The impact of a mixed convection magnetic field and an electrical double layer has combined for momentum conduct. Flow is produced in an axial direction by the movement of the upper wall. The important findings are:

• When the magnetic parameter and nanoparticle volume fraction are increased, then the velocity of the nanofluid decreases whereas the temperature profile is increased.
• Velocity profile is increased for increasing PVC while a decrease in temperature is detected.
• Temperature and velocity demonstrate similar behavior for increasing values of $\kappa$ and the ratio between $U_{Hs}$ and $u_m$.
• It is observed that $C_f$ increases at the heated wall against higher Brinkman number and volume fraction while the reverse behavior is noted for the increasing ratio between $U_{Hs}$ and $u_m$. The same phenomena are observed for the cases of electro-osmotic and magnetic factors.
• Skin friction is improved with increasing values of $\kappa$ and the ratio between $U_{Hs}$ and $u_m$, whereas it decreases with the increase in Brinkman number, volume fraction and the magnetic parameter.
• The Nusselt number escalates for a snowballing magnetic parameter but de-escalates with the increasing ratio between $U_{Hs}$ and $u_m$, volume fraction, Brinkman number and electro-osmotic factors.
• The entropy generation increases with an increase of volumetric volume expansion $\beta$, magnetic field $M$ and $\kappa$, while it decreases with an increase of $Br{\Omega }^{-1}$ and Brinkman number.
• A dual behavior of entropy generation is noted for decreasing and increasing values of $R_{\zeta }$.
• The Bejan number escalates by snowballing values of both $Br{\Omega }^{-1}$ and magnetic elements in direct relation with each other and is depicted for both of them.