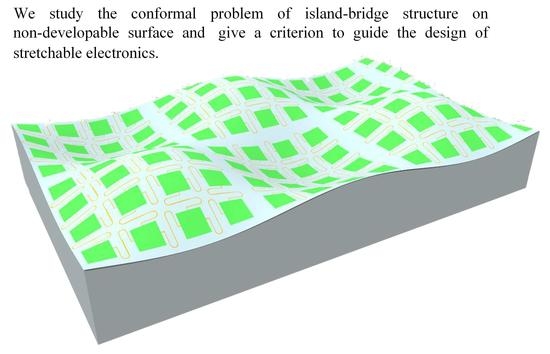
The Conformal Design of an Island-Bridge Structure on a Non-Developable Surface for Stretchable Electronics
Abstract
:1. Introduction
2. Conformal Criterion for Island
2.1. Conformal Modelling for Island
2.2. Adhesion Experiment for Island
3. Mechanics of Stretchable Bridges
3.1. Tensile Stiffness Design for Bridges
3.2. Stretchability Demands for Bridges
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Conformal Strain Energy with Angle of Deviation


Appendix B. Relative Error between Approximate Solution and Exact Solution

Appendix C. Material Parameter Test

References
- Jung, I.; Xiao, J.; Malyarchuk, V.; Lu, C.; Li, M.; Liu, Z.; Yoon, J.; Huang, Y.; Rogers, J.A. Dynamically tunable hemispherical electronic eye camera system with adjustable zoom capability. Proc. Natl. Acad. Sci. USA 2011, 108, 1788–1793. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ko, H.C.; Stoykovich, M.P.; Song, J.; Malyarchuk, V.; Choi, W.M.; Yu, C.-J.; Geddes, J.B.; Xiao, J.; Wang, S.; Huang, Y.; et al. A hemispherical electronic eye camera based on compressible silicon optoelectronics. Nature 2008, 454, 748–753. [Google Scholar] [CrossRef] [PubMed]
- Song, Y.M.; Xie, Y.; Malyarchuk, V.; Xiao, J.; Jung, I.; Choi, K.-J.; Liu, Z.; Park, H.; Lu, C.; Kim, R.-H.; et al. Digital cameras with designs inspired by the arthropod eye. Nature 2013, 497, 95–99. [Google Scholar] [CrossRef] [PubMed]
- Xu, L.; Gutbrod, S.R.; Bonifas, A.P.; Su, Y.; Sulkin, M.S.; Lu, N.; Chung, H.-J.; Jang, K.-I.; Liu, Z.; Ying, M.; et al. 3D multifunctional integumentary membranes for spatiotemporal cardiac measurements and stimulation across the entire epicardium. Nat. Commun. 2014, 5, 3329. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Xu, L.; Gutbrod, S.R.; Ma, Y.; Petrossians, A.; Liu, Y.; Webb, R.C.; Fan, J.A.; Yang, Z.; Xu, R.; Whalen, J.J.; et al. Materials and fractal designs for 3D multifunctional integumentary membranes with capabilities in cardiac electrotherapy. Adv. Mater. 2015, 27, 1731–1737. [Google Scholar] [CrossRef] [PubMed]
- Son, D.; Lee, J.; Qiao, S.; Ghaffari, R.; Kim, J.; Lee, J.E.; Song, C.; Kim, S.J.; Lee, D.J.; Jun, S.W.; et al. Multifunctional wearable devices for diagnosis and therapy of movement disorders. Nat. Nanotechnol. 2014, 9, 397–404. [Google Scholar] [CrossRef] [PubMed]
- Someya, T.; Kato, Y.; Sekitani, T.; Iba, S.; Noguchi, Y.; Murase, Y.; Kawaguchi, H.; Sakurai, T. Conformable, flexible, large-area networks of pressure and thermal sensors with organic transistor active matrixes. Proc. Natl. Acad. Sci. USA 2005, 102, 12321–12325. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Dagdeviren, C.; Su, Y.; Joe, P.; Yona, R.; Liu, Y.; Kim, Y.S.; Huang, Y.; Damadoran, A.R.; Xia, J.; Martin, L.W.; et al. Conformable amplified lead zirconate titanate sensors with enhanced piezoelectric response for cutaneous pressure monitoring. Nat. Commun. 2014, 5, 4496. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Li, Y.; Samad, Y.A.; Liao, K. From cotton to wearable pressure sensor. J. Mater. Chem. A 2015, 3, 2181–2187. [Google Scholar] [CrossRef]
- Samad, Y.A.; Li, Y.; Alhassan, S.M.; Liao, K. Novel graphene foam composite with adjustable sensitivity for sensor applications. ACS Appl. Mater. Interfaces 2015, 7, 9195–9202. [Google Scholar] [CrossRef] [PubMed]
- Boland, C.S.; Khan, U.; Ryan, G.; Barwich, S.; Charifou, R.; Harvey, A.; Backes, C.; Li, Z.; Ferreira, M.S.; Mobius, M.E.; et al. Sensitive electromechanical sensors using viscoelastic graphene-polymer nanocomposites. Science 2016, 354, 1257–1260. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lanzara, G.; Salowitz, N.; Guo, Z.; Chang, F.K. A spider-web-like highly expandable sensor network for multifunctional materials. Adv. Mater. 2010, 22, 4643–4648. [Google Scholar] [CrossRef] [PubMed]
- Salowitz, N.; Guo, Z.; Roy, S.; Nardari, R.; Li, Y.-H.; Kim, S.-J.; Kopsaftopoulos, F.; Chang, F.-K. Recent advancements and vision toward stretchable bio-inspired networks for intelligent structures. Struct. Health Monit. 2014, 13, 609–620. [Google Scholar] [CrossRef]
- Kim, D.H.; Lu, N.; Ma, R.; Kim, Y.S.; Kim, R.H.; Wang, S.; Wu, J.; Won, S.M.; Tao, H.; Islam, A.; et al. Epidermal electronics. Science 2011, 333, 838–843. [Google Scholar] [CrossRef] [PubMed]
- Jeong, J.-W.; Kim, M.K.; Cheng, H.; Yeo, W.-H.; Huang, X.; Liu, Y.; Zhang, Y.; Huang, Y.; Rogers, J.A. Capacitive epidermal electronics for electrically safe, long-term electrophysiological measurements. Adv. Healthc. Mater. 2014, 3, 642–648. [Google Scholar] [CrossRef] [PubMed]
- Wang, S.; Li, M.; Wu, J.; Kim, D.-H.; Lu, N.; Su, Y.; Kang, Z.; Huang, Y.; Rogers, J.A. Mechanics of epidermal electronics. J. Appl. Mech. 2012, 79, 031022. [Google Scholar] [CrossRef]
- Dong, W.; Xiao, L.; Zhu, C.; Ye, D.; Wang, S.; Huang, Y.; Yin, Z. Theoretical and experimental study of 2D conformability of stretchable electronics laminated onto skin. Sci. China Technol. Sci. 2017, 60, 1415–1422. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, J.; Xing, Y.; Song, J. Thermomechanical analysis of epidermal electronic devices integrated with human skin. J. Appl. Mech. 2017, 84, 111004. [Google Scholar] [CrossRef]
- Majidi, C.; Fearing, R.S. Adhesion of an elastic plate to a sphere. Proc. R. Soc. A 2008, 464, 1309–1317. [Google Scholar] [CrossRef] [Green Version]
- Hure, J.; Audoly, B. Capillary buckling of a thin film adhering to a sphere. J. Mech. Phys. Solids 2013, 61, 450–471. [Google Scholar] [CrossRef] [Green Version]
- Zhou, Y.; Chen, Y.; Liu, B.; Wang, S.; Yang, Z.; Hu, M. Mechanics of nanoscale wrinkling of graphene on a non-developable surface. Carbon 2015, 84, 263–271. [Google Scholar] [CrossRef] [Green Version]
- Chen, Y.; Ma, Y.; Wang, S.; Zhou, Y.; Liu, H. The morphology of graphene on a non-developable concave substrate. Appl. Phys. Lett. 2016, 108, 031905. [Google Scholar] [CrossRef]
- Hure, J.; Roman, B.; Bico, J. Stamping and wrinkling of elastic plates. Phys. Rev. Lett. 2012, 109, 054302. [Google Scholar] [CrossRef] [PubMed]
- Hure, J.; Roman, B.; Bico, J. Wrapping an adhesive sphere with an elastic sheet. Phys. Rev. Lett. 2011, 106, 174301. [Google Scholar] [CrossRef] [PubMed]
- Mitchell, N.P.; Koning, V.; Vitelli, V.; Irvine, W.T.M. Fracture in sheets draped on curved surfaces. Nat. Mater. 2016, 16, 89–93. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kim, D.-H.; Song, J.; Choi, W.M.; Kim, H.-S.; Kim, R.-H.; Liu, Z.; Huang, Y.Y.; Hwang, K.-C.; Zhang, Y.; Rogers, J.A. Materials and noncoplanar mesh designs for integrated circuits with linear elastic responses to extreme mechanical deformations. Proc. Natl. Acad. Sci. USA 2008, 105, 18675–18680. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Su, Y.; Wang, S.; Huang, Y.; Luan, H.; Dong, W.; Fan, J.A.; Yang, Q.; Rogers, J.A.; Huang, Y. Elasticity of fractal inspired interconnects. Small 2015, 11, 367–373. [Google Scholar] [CrossRef] [PubMed]
- Shi, X.; Xu, R.; Li, Y.; Zhang, Y.; Ren, Z.; Gu, J.; Rogers, J.A.; Huang, Y. Mechanics design for stretchable, high areal coverage gaas solar module on an ultrathin substrate. J. Appl. Mech. 2014, 81, 124502. [Google Scholar] [CrossRef]
- Li, R.; Li, M.; Su, Y.; Song, J.; Ni, X. An analytical mechanics model for the island-bridge structure of stretchable electronics. Soft Matter 2013, 9, 8476–8482. [Google Scholar] [CrossRef]
- Ma, Y.; Feng, X.; Rogers, J.A.; Huang, Y.; Zhang, Y. Design and application of ‘j-shaped’ stress-strain behavior in stretchable electronics: A review. Lab Chip 2017, 17, 1689–1704. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Xu, S.; Fu, H.; Lee, J.; Su, J.; Hwang, K.C.; Rogers, J.A.; Huang, Y. Buckling in serpentine microstructures and applications in elastomer-supported ultra-stretchable electronics with high areal coverage. Soft Matter 2013, 9, 8062–8070. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Dong, W.; Zhu, C.; Ye, D.; Huang, Y. Optimal design of self-similar serpentine interconnects embedded in stretchable electronics. Appl. Phys. A 2017, 123, 428. [Google Scholar] [CrossRef]
- Dong, W.; Wang, Y.; Zhou, Y.; Bai, Y.; Ju, Z.; Guo, J.; Gu, G.; Bai, K.; Ouyang, G.; Chen, S.; et al. Soft human–machine interfaces: Design, sensing and stimulation. Int. J. Intell. Rob. Appl. 2018. [Google Scholar] [CrossRef]
- Ma, Q.; Zhang, Y. Mechanics of fractal-inspired horseshoe microstructures for applications in stretchable electronics. J. Appl. Mech. 2016, 83, 111008. [Google Scholar] [CrossRef]
- Zhang, Y.; Huang, Y.; Rogers, J.A. Mechanics of stretchable batteries and supercapacitors. Curr. Opin. Solid State Mater. Sci. 2015, 19, 190–199. [Google Scholar] [CrossRef]
- Chen, Z.; Guo, Q.; Majidi, C.; Chen, W.; Srolovitz, D.J.; Haataja, M.P. Nonlinear geometric effects in mechanical bistable morphing structures. Phys. Rev. Lett. 2012, 109, 114302. [Google Scholar] [CrossRef] [PubMed]
- Kim, D.H.; Xiao, J.; Song, J.; Huang, Y.; Rogers, J.A. Stretchable, curvilinear electronics based on inorganic materials. Adv. Mater. 2010, 22, 2108–2124. [Google Scholar] [CrossRef] [PubMed]
- Yu, K.J.; Yan, Z.; Han, M.; Rogers, J.A. Inorganic semiconducting materials for flexible and stretchable electronics. npj Flex. Electron. 2017, 1, 4. [Google Scholar] [CrossRef]
- Huang, Y.; Liu, H.; Xu, Z.; Chen, J.; Yin, Z. Conformal peeling of device-on-substrate system in flexible electronic assembly. IEEE Trans. Compon. Packag. Manuf. Technol. 2018, PP, 1–11. [Google Scholar] [CrossRef]







© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xiao, L.; Zhu, C.; Xiong, W.; Huang, Y.; Yin, Z. The Conformal Design of an Island-Bridge Structure on a Non-Developable Surface for Stretchable Electronics. Micromachines 2018, 9, 392. https://doi.org/10.3390/mi9080392
Xiao L, Zhu C, Xiong W, Huang Y, Yin Z. The Conformal Design of an Island-Bridge Structure on a Non-Developable Surface for Stretchable Electronics. Micromachines. 2018; 9(8):392. https://doi.org/10.3390/mi9080392
Chicago/Turabian StyleXiao, Lin, Chen Zhu, Wennan Xiong, YongAn Huang, and Zhouping Yin. 2018. "The Conformal Design of an Island-Bridge Structure on a Non-Developable Surface for Stretchable Electronics" Micromachines 9, no. 8: 392. https://doi.org/10.3390/mi9080392