Electroosmotic Flow of Viscoelastic Fluid through a Constriction Microchannel
Abstract
:1. Introduction
2. Mathematical Model
3. Numerical Method and Code Validation
- Step 1. Initialize the fields and time ().
- Step 1.1. Compute steady state from Equation (9) and from Equation (8).
- Step 2. Enter the time loop ().
- Step 2.1. Enter the inner iteration loop ().
- Step 2.1.1. Compute and by log-conformation method.
- Step 2.1.2. Compute estimated velocity field by solving the momentum equation.
- Step 2.1.3. ompute pressure field by enforcing the continuity equation.
- Step 2.1.4. Correct the previously estimated velocity field using the correct pressure field.
- Step 2.1.5. Increase the inner iteration index () and repeat the computation from Step 2.1.1, until the inner iteration criteria (i.e., maximum tolerance) is satisfied.
- Step 2.1.6. Set .
- Step 2.2. Increase time, , and return to Step 2.1 until the simulation time is reached.
- Step 3. Stop the simulation and exit.
4. Results and Discussion
4.1. Instability of PAA Solutions
4.2. Elastic Instabilities under Various and
5. Conclusions
- (1)
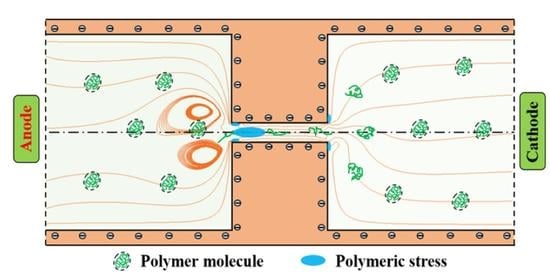
- When polyacrylamide (PAA) concentration (applied electric field) exceeds a critical value, the EOF of viscoelastic fluid becomes time-dependent with upstream vortices occurring in the inlet reservoir near the entrance of the constriction microchannel. In contrast, EOF of Newtonian fluid is always in a steady state without vortices.
- (2)
- For the viscoelastic EOF, significant polymer stress is induced near the entrance within the constriction and near the downstream lips of the constriction, causing the elastic instabilities of the viscoelastic EOF. The induced polymer stress is dramatically magnified with the increase of polymer concentration and applied electric field. However, the increase of polymer concentration shows a more significant enhancing effect on the polymer stress than the increase of applied electric field.
- (3)
- The EOF velocity of viscoelastic fluid within the constriction becomes temporally and spatially dependent. Near the exit of the constriction, due to the extrudate swell effect of the polymers, the velocity at the centerline first decreases at the exit followed by an increase in the outlet reservoir.
- (4)
- The velocity at the exit of the constriction is higher than that at the entrance of the constriction because of the formation of upstream vortices, which is in qualitative agreement with experimental observation obtained from the literature.
- (5)
- Under the same total viscosity and applied electric field, the velocity of Newtonian fluid is higher than that of viscoelastic fluid, which is attributed to the induced polymeric stress within the constriction. When the applied electric field is less than 300 V/cm, the Helmholtz–Smoluchowski velocity formula can predict the cross-sectional average velocity of viscoelastic fluid with PAA concentration up to 500 ppm, and the relative error is less than 5%. At a fixed PAA concentration, in general the relative error of the Helmholtz–Smoluchowski approximation increases with an increase in the applied electric field.
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
Appendix A.1. Mesh Independence Study



Appendix A.2. Boundary Conditions

Appendix A.3. Analytical Solution of Afonso et al
Appendix A.4. Summary of Current Studies
| Geometry | Fluids | Electrical Parameters | Instabilities |
|---|---|---|---|
| Constriction channel [32] Contraction ratio: 2:1 Width: 200 μm and 100 μm Depth: 20 μm | PAA (18 × 106 and 5 × 106 Da) with 20:80 vol.% methanol: water mixture. 1–480 ppm. | Electro-osmotic mobility: , , and for polymer free, high molecular weight, and low molecular weight 120 ppm PAA solutions. Electric field: 0–900 V/cm. |
|
| Cross slot channel [34,35] Width: 100 μm Height: 50 μm | PAA, 5 × 106 Da, 300 and 1000 ppm. | Electro-osmotic mobility: , for 1000 ppm and 300 ppm PAA solutions. . |
|
| T-shaped channel [37] Main-branch: Width: 200 μm Depth: 30 μm Side-branch 1: Width: 100 μm Depth: 50 μm Side-branch 2: Width: 100 μm Depth: 67 μm | Phosphate buffer-based aqueous polymer solutions. (500 ppm XG, 5% PVP, 2000 ppm PEO, 200 ppm PAA, 1000 ppm hyaluronic acid(HA)). | Electro-osmotic mobility: and for XG, PVP, HA, PEO, PAA solutions. . |
|
| Constriction channel [38] Contraction ratio: 10:1 Width: 400 μm and 40 μm Depth: 40 μm depth Length of constriction: 200 μm | 1 mM phosphate buffer-based aqueous polymer solutions. (2000 ppm XG, 5% PVP, 3000 ppm PEO, and 200 ppm PAA.) | Electro-osmotic mobility: , , for buffer, XG, PVP, PEO, PAA solutions. Electric field: 100–400 V/cm |
|
| Hyperbolic/abrupt contraction with abrupt/hyperbolic expansion [39] Channel 1: (7.2:1) Width: 401 μm and 56 μm Depth: 100 μm Length of constriction: 382 μm Channel 2: (22.4:1) Width: 403 μm and 18 μm Depth: 100 μm Length of constriction: 128 μm | 1 mM borate buffer with 0.05% wt. sodiumdodecylsulfate. 100, 300, 1000, and 10,000 ppm PAA solutions. | Electro conductivity: 20.2, 55.5, 178.3 and 161.8 μS/cm for 100, 300, 1000, and 10,000 ppm PAA solutions. . |
|
Appendix A.5. Results for Zeta potentials of −70 mV and −150 mV



Appendix A.6. Dimensionless Numbers

References
- Gao, M.; Gui, L. A handy liquid metal based electroosmotic flow pump. Lab Chip 2014, 14, 1866–1872. [Google Scholar] [CrossRef] [PubMed]
- Peng, R.; Li, D. Effects of ionic concentration gradient on electroosmotic flow mixing in a microchannel. J. Colloid Interface. Sci. 2015, 440, 126–132. [Google Scholar] [CrossRef] [Green Version]
- Palyulin, V.V.; Ala-Nissila, T.; Metzler, R. Polymer translocation: The first two decades and the recent diversification. Soft Matter. 2014, 10, 9016–9037. [Google Scholar] [CrossRef] [Green Version]
- Takamura, Y.; Onoda, H.; Inokuchi, H.; Adachi, S.; Oki, A.; Horiike, Y. Low-voltage electroosmosis pump for stand-alone microfluidics devices. Electrophoresis 2003, 24, 185–192. [Google Scholar] [CrossRef] [PubMed]
- Li, L.; Wang, X.; Pu, Q.; Liu, S. Advancement of electroosmotic pump in microflow analysis: A review. Anal. Chim. Acta 2019, 1060, 1–16. [Google Scholar] [CrossRef]
- Jiang, H.; Weng, X.; Chon, C.H.; Wu, X.; Li, D. A microfluidic chip for blood plasma separation using electro-osmotic flow control. J. Micromech. Microeng. 2011, 21, 085019. [Google Scholar] [CrossRef]
- Ermann, N.; Hanikel, N.; Wang, V.; Chen, K.; Weckman, N.E.; Keyser, U.F. Promoting single-file DNA translocations through nanopores using electro-osmotic flow. J. Chem. Phys. 2018, 149, 163311. [Google Scholar] [CrossRef] [PubMed]
- Huang, G.; Willems, K.; Soskine, M.; Wloka, C.; Maglia, G. Electro-osmotic capture and ionic discrimination of peptide and protein biomarkers with FraC nanopores. Nat. Commun. 2017, 8, 1–11. [Google Scholar] [CrossRef]
- Buyukdagli, S. Facilitated polymer capture by charge inverted electroosmotic flow in voltage-driven polymer translocation. Soft Matter. 2018, 14, 3541–3549. [Google Scholar] [CrossRef] [PubMed]
- Bello, M.S.; Besi, P.D.; Rezzonico, R.; Righetti, P.G.; Casiraghi, E. Electroosmosis of polymer solutions in fused silica capillaries. Electrophoresis 1994, 15, 623–626. [Google Scholar] [CrossRef]
- Chang, F.M.; Tsao, H.K. Drag reduction in electro-osmosis of polymer solutions. Appl. Phys. Lett. 2007, 90, 194105. [Google Scholar] [CrossRef]
- Kamişli, F. Flow analysis of a power-law fluid confined in an extrusion die. Int. J. Eng. Sci. 2003, 41, 1059–1083. [Google Scholar] [CrossRef]
- Zimmerman, W.; Rees, J.; Craven, T. Rheometry of non-Newtonian electrokinetic flow in a microchannel T-junction. Microfluid. Nanofluid. 2006, 2, 481–492. [Google Scholar] [CrossRef]
- Hakim, A. Mathematical analysis of viscoelastic fluids of White-Metzner type. J. Math. Anal. Appl. 1994, 185, 675–705. [Google Scholar] [CrossRef] [Green Version]
- Das, M.; Jain, V.; Ghoshdastidar, P. Fluid flow analysis of magnetorheological abrasive flow finishing (MRAFF) process. Int. J. Mach. Tool. Manu. 2008, 48, 415–426. [Google Scholar] [CrossRef]
- Oldroyd, J.G. On the formulation of rheological equations of state. Proc. Math. Phys. Eng. Sci. 1950, 200, 523–541. [Google Scholar]
- Thien, N.P.; Tanner, R.I. A new constitutive equation derived from network theory. J. Non-Newton. Fluid Mech. 1977, 2, 353–365. [Google Scholar] [CrossRef]
- Koszkul, J.; Nabialek, J. Viscosity models in simulation of the filling stage of the injection molding process. J. Mater. Process. Technol. 2004, 157, 183–187. [Google Scholar] [CrossRef]
- Öztekin, A.; Brown, R.A.; McKinley, G.H. Quantitative prediction of the viscoelastic instability in cone-and-plate flow of a Boger fluid using a multi-mode Giesekus model. J. Non-Newton. Fluid Mech. 1994, 54, 351–377. [Google Scholar] [CrossRef]
- Das, S.; Chakraborty, S. Analytical solutions for velocity, temperature and concentration distribution in electroosmotic microchannel flows of a non-Newtonian bio-fluid. Anal. Chim. Acta 2006, 559, 15–24. [Google Scholar] [CrossRef]
- Zhao, C.; Zholkovskij, E.; Masliyah, J.H.; Yang, C. Analysis of electroosmotic flow of power-law fluids in a slit microchannel. J. Colloid Interface Sci. 2008, 326, 503–510. [Google Scholar] [CrossRef]
- Zhao, C.; Yang, C. An exact solution for electroosmosis of non-Newtonian fluids in microchannels. J. Non-Newton. Fluid Mech. 2011, 166, 1076–1079. [Google Scholar] [CrossRef]
- Zhao, C.; Yang, C. Joule heating induced heat transfer for electroosmotic flow of power-law fluids in a microcapillary. Int. J. Heat Fluid Flow 2012, 55, 2044–2051. [Google Scholar] [CrossRef]
- Zhao, C.; Yang, C. Electroosmotic flows of non-Newtonian power-law fluids in a cylindrical microchannel. Electrophoresis 2013, 34, 662–667. [Google Scholar] [CrossRef]
- Olivares, M.L.; Vera-Candioti, L.; Berli, C.L. The EOF of polymer solutions. Electrophoresis 2009, 30, 921–928. [Google Scholar] [CrossRef]
- Tang, G.; Li, X.; He, Y.; Tao, W. Electroosmotic flow of non-Newtonian fluid in microchannels. J. Non-Newton. Fluid Mech. 2009, 157, 133–137. [Google Scholar] [CrossRef]
- Park, H.; Lee, W. Effect of viscoelasticity on the flow pattern and the volumetric flow rate in electroosmotic flows through a microchannel. Lab Chip 2008, 8, 1163–1170. [Google Scholar] [CrossRef]
- Afonso, A.; Alves, M.; Pinho, F. Analytical solution of mixed electro-osmotic/pressure driven flows of viscoelastic fluids in microchannels. J. Non-Newton. Fluid Mech. 2009, 159, 50–63. [Google Scholar] [CrossRef]
- Afonso, A.; Alves, M.; Pinho, F. Electro-osmotic flow of viscoelastic fluids in microchannels under asymmetric zeta potentials. J. Eng. Math. 2011, 71, 15–30. [Google Scholar] [CrossRef]
- Liu, Q.; Jian, Y.; Yang, L. Alternating current electroosmotic flow of the Jeffreys fluids through a slit microchannel. Phys. Fluids 2011, 23, 102001. [Google Scholar] [CrossRef]
- Sousa, J.; Afonso, A.; Pinho, F.; Alves, M. Effect of the skimming layer on electro-osmotic-Poiseuille flows of viscoelastic fluids. Microfluid. Nanofluidics 2011, 10, 107–122. [Google Scholar] [CrossRef]
- Bryce, R.; Freeman, M. Extensional instability in electro-osmotic microflows of polymer solutions. Phys. Rev. E 2010, 81, 036328. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bryce, R.; Freeman, M. Abatement of mixing in shear-free elongationally unstable viscoelastic microflows. Lab Chip 2010, 10, 1436–1441. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Pimenta, F.; Alves, M. Stabilization of an open-source finite-volume solver for viscoelastic fluid flows. J. Non-Newton. Fluid Mech. 2017, 239, 85–104. [Google Scholar] [CrossRef]
- Pimenta, F.; Alves, M. Electro-elastic instabilities in cross-shaped microchannels. J. Non-Newton. Fluid Mech. 2018, 259, 61–77. [Google Scholar] [CrossRef]
- Song, L.; Jagdale, P.; Yu, L.; Liu, Z.; Li, D.; Zhang, C.; Xuan, X. Electrokinetic instability in microchannel viscoelastic fluid flows with conductivity gradients. Phys. Fluids 2019, 31, 082001. [Google Scholar]
- Song, L.; Yu, L.; Li, D.; Jagdale, P.; Xuan, X. Elastic instabilities in the electroosmotic flow of non-Newtonian fluids through T-shaped microchannels. Electrophoresis 2020, 41, 588–597. [Google Scholar] [CrossRef]
- Ko, C.H.; Li, D.; Malekanfard, A.; Wang, Y.N.; Fu, L.M.; Xuan, X. Electroosmotic flow of non-Newtonian fluids in a constriction microchannel. Electrophoresis 2019, 40, 1387–1394. [Google Scholar] [CrossRef]
- Sadek, S.H.; Pinho, F.T.; Alves, M.A. Electro-elastic flow instabilities of viscoelastic fluids in contraction/expansion micro-geometries. J. Non-Newton. Fluid Mech. 2020, 283, 104293. [Google Scholar] [CrossRef]
- Afonso, A.; Pinho, F.; Alves, M. Electro-osmosis of viscoelastic fluids and prediction of electro-elastic flow instabilities in a cross slot using a finite-volume method. J. Non-Newton. Fluid Mech. 2012, 179, 55–68. [Google Scholar] [CrossRef]
- Huang, Y.; Chen, J.T.; Wong, T.; Liow, J.L. Experimental and theoretical investigations of non-Newtonian electro-osmotic driven flow in rectangular microchannels. Soft Matter. 2016, 12, 6206–6213. [Google Scholar] [CrossRef]
- Ronshin, F.; Chinnow, E. Experimental characterization of two-phase flow patterns in a slit microchannel. Exp. Therm. Fluid Sci. 2019, 103, 262–273. [Google Scholar] [CrossRef]
- Nito, F.; Shiozaki, T.; Nagura, R.; Tsuji, T.; Doi, K.; Hosokawa, C.; Kawano, S. Quantitative evaluation of optical forces by single particle tracking in slit-like microfluidic channels. J. Phys. Chem. C 2018, 122, 17963–17975. [Google Scholar] [CrossRef]
- Sánchez, S.; Arcos, J.; Bautista, O.; Méndez, F. Joule heating effect on a purely electroosmotic flow of non-Newtonian fluids in a slit microchannel. J. Non-Newton. Fluid Mech. 2013, 192, 1–9. [Google Scholar] [CrossRef]
- Varagnolo, S.; Filippi, D.; Mistura, G.; Pierno, M.; Sbragaglia, M. Stretching of viscoelastic drops in steady sliding. Soft Matter. 2017, 13, 3116–3124. [Google Scholar] [CrossRef] [Green Version]
- Fattal, R.; Kupferman, R. Constitutive laws for the matrix-logarithm of the conformation tensor. J. Non-Newton. Fluid Mech. 2004, 123, 281–285. [Google Scholar] [CrossRef]
- Fattal, R.; Kupferman, R. Time-dependent simulation of viscoelastic flows at high Weissenberg number using the log-conformation representation. J. Non-Newton. Fluid Mech. 2005, 126, 23–37. [Google Scholar] [CrossRef]
- Walters, K.; Webster, M.F. The distinctive CFD challenges of computational rheology. Int. J. Numer. Meth. Fluids. 2003, 43, 577–596. [Google Scholar] [CrossRef]
- Fogolari, F.; Brigo, A.; Molinari, H. The Poisson–Boltzmann equation for biomolecular electrostatics: A tool for structural biology. J. Mol. Recognit. 2002, 15, 377–392. [Google Scholar] [CrossRef]
- Pimenta, F.; Alves, M.A. Numerical simulation of electrically-driven flows using OpenFOAM. arXiv 2018, arXiv:1802.02843. [Google Scholar]
- Alves, M.; Oliveira, P.; Pinho, F. A convergent and universally bounded interpolation scheme for the treatment of advection. Int. J. Numer. Methods Fluids 2003, 41, 47–75. [Google Scholar] [CrossRef]
- Duarte, A.; Miranda, A.I.; Oliveira, P.J. Numerical and analytical modeling of unsteady viscoelastic flows: The start-up and pulsating test case problems. J. Non-Newton. Fluid Mech. 2008, 154, 153–169. [Google Scholar] [CrossRef] [Green Version]
- Patankar, S.V.; Corp, H.P. Numerical Heat Transfer and Fluid Flow, 1st ed.; McGraw-Hill: New York, NY, USA, 1980. [Google Scholar]
- Van Doormaal, J.P.; Raithby, G.D. Enhancements of the SIMPLE method for predicting incompressible fluid flows. Numer. Heat Transf. 1987, 7, 147–163. [Google Scholar]
- López-Herrera, J.; Popinet, S.; Castrejón-Pita, A. An adaptive solver for viscoelastic incompressible two-phase problems applied to the study of the splashing of weakly viscoelastic droplets. J. Non-Newton. Fluid Mech. 2019, 264, 144–158. [Google Scholar] [CrossRef]
- Sousa, P.C.; Vega, E.J.; Sousa, R.G.; Montanero, J.M.; Alves, M.A. Measurement of relaxation times in extensional flow of weakly viscoelastic polymer solutions. Rheol. Acta 2017, 56, 11–20. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Martins, F.; Oishi, C.M.; Afonso, A.M.; Alves, M.A. A numerical study of the kernel-conformation transformation for transient viscoelastic fluid flow. J. Comput. Phys. 2015, 302, 653–673. [Google Scholar] [CrossRef] [Green Version]
- Sze, A.; Erickson, D.; Ren, L.; Li, D. Zeta-potential measurement using the Smoluchowski equation and the slope of the current–time relationship in electroosmotic flow. J. Colloid Interface Sci. 2003, 261, 402–410. [Google Scholar] [CrossRef]
- Sirisinha, C. A review of extrudate swell in polymers. J. Sci. Soc. Thailand. 1997, 23, 259–280. [Google Scholar] [CrossRef]
- James, D.F. N1 stresses in extensional flows. J. Non-Newton. Fluid Mech. 2016, 232, 33–42. [Google Scholar] [CrossRef]
- Bird, R.B.; Armstrong, R.C.; Hassager, O. Dynamics of polymeric liquids. In Fluid Mechanics, 2nd ed.; Wiley-Interscience: Hoboken, NJ, USA, 1987; Volume 1. [Google Scholar]
- Latinwo, F.; Schroeder, C.M. Determining elasticity from single polymer dynamics. Soft Matter. 2014, 10, 2178–2187. [Google Scholar] [CrossRef] [Green Version]
- Groisman, A.; Steinberg, V. Efficient mixing at low Reynolds numbers using polymer additives. Nature 2001, 410, 905–908. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Grilli, M.; Vázquez-Quesada, A.; Ellero, M. Transition to turbulence and mixing in a viscoelastic fluid flowing inside a channel with a periodic array of cylindrical obstacles. Phys. Rev. Lett. 2013, 110, 174501. [Google Scholar] [CrossRef] [PubMed]
- Burghelea, T.; Segre, E.; Steinberg, V. Elastic turbulence in von Karman swirling flow between two disks. Phys. Fluids 2007, 19, 053104. [Google Scholar] [CrossRef] [Green Version]
- Pakdel, P.; McKinley, G.H. Elastic instability and curved streamlines. Phys. Rev. Lett. 1996, 77, 2459. [Google Scholar] [CrossRef] [PubMed]
- Jovanović, M.R.; Kumar, S. Nonmodal amplification of stochastic disturbances in strongly elastic channel flows. J. Non-Newton. Fluid Mech. 2011, 166, 755–778. [Google Scholar] [CrossRef] [Green Version]
















| 100 | 200 | 300 | 400 | 500 | 600 | |
|---|---|---|---|---|---|---|
| Minimum relative error | 1.0% | 1.3% | 1.8% | 5.5% | 7.0% | 8.5% |
| Average relative error | 1.3% | 1.6% | 2.3% | 5.9% | 7.7% | 8.9% |
| Maximum relative error | 1.5% | 1.9% | 2.8% | 6.5% | 8.2% | 9.6% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ji, J.; Qian, S.; Liu, Z. Electroosmotic Flow of Viscoelastic Fluid through a Constriction Microchannel. Micromachines 2021, 12, 417. https://doi.org/10.3390/mi12040417
Ji J, Qian S, Liu Z. Electroosmotic Flow of Viscoelastic Fluid through a Constriction Microchannel. Micromachines. 2021; 12(4):417. https://doi.org/10.3390/mi12040417
Chicago/Turabian StyleJi, Jianyu, Shizhi Qian, and Zhaohui Liu. 2021. "Electroosmotic Flow of Viscoelastic Fluid through a Constriction Microchannel" Micromachines 12, no. 4: 417. https://doi.org/10.3390/mi12040417