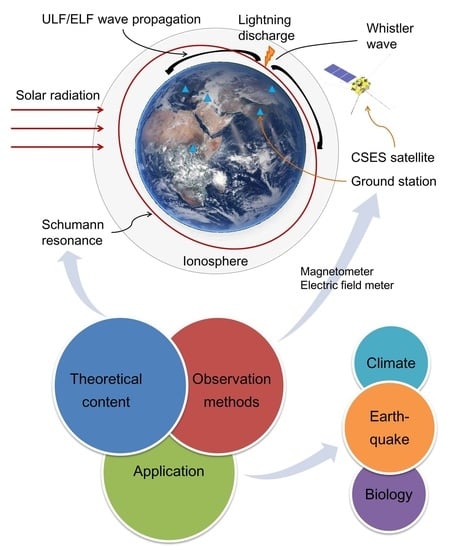
Recent Advances and Challenges in Schumann Resonance Observations and Research
Abstract
:1. Introduction
2. Observation Methods
2.1. Ground Observation
2.2. Satellite Observation
3. Schumann Resonance and Lightning
4. The Application of Schumann Resonance
4.1. The Correlation of Anomalies in Schumann Resonances and Earthquakes
4.2. Application of Schumann Resonance in Other Fields
5. Summary and Prospect
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Nickolaenko, A.P.; Hayakawa, M. Resonances in the Earth-Ionosphere Cavity; Kluwer Academic Publishers: Dordrecht, The Netherlands; Boston, MA, USA; London, UK, 2002. [Google Scholar]
- Sátori, G.; Williams, E.; Mushtak, V. Response of the Earth–Ionosphere Cavity Resonator to the 11-Year Solar Cycle in X-Radiation. J. Atmos. Sol.-Terr. Phys. 2005, 67, 553–562. [Google Scholar] [CrossRef]
- Tran, A.; Polk, C. Schumann Resonances and Electrical Conductivity of the Atmospher and Lower Ionosphere—I. Effects of Conductivity at Various Altitudes on Resonance Frequencies and Attenuation. J. Atmos. Terr. Phys. 1979, 41, 1241–1248. [Google Scholar] [CrossRef]
- Yang, H. Three-Dimensional Finite Difference Time Domain Modeling of the Earth-Ionosphere Cavity Resonances. Geophys. Res. Lett. 2005, 32, L03114. [Google Scholar] [CrossRef] [Green Version]
- Galejs, J. ELF Waves in the Presence of Exponential Ionospheric Conductivity Profiles. IRE Trans. Antennas Propag. 1961, 9, 554–562. [Google Scholar] [CrossRef]
- Bennett, A.J.; Harrison, R.G. Surface Measurement System for the Atmospheric Electrical Vertical Conduction Current Density, with Displacement Current Density Correction. J. Atmos. Sol.-Terr. Phys. 2008, 70, 1373–1381. [Google Scholar] [CrossRef]
- George, F.F.G. Physics at the British Association. Nature 1893, 48, 525–529. [Google Scholar] [CrossRef] [Green Version]
- Larmor, J. Electric Vibrations in Condensing Dielectric Systems. Math. Phys. Pap. 1929, 1, 356–378. [Google Scholar]
- Wilson, C.T.R., III. Investigations on Lighting Discharges and on the Electric Field of Thunderstorms. Philos. Trans. R. Soc. Lond. Ser. Contain. Pap. Math. Phys. Character 1921, 221, 73–115. [Google Scholar] [CrossRef]
- Schelkunoff, S.A. Ultrashort Electromagnetic Waves IV—Guided Propagation. Electr. Eng. 1943, 62, 235–246. [Google Scholar] [CrossRef]
- Rydbeck, O.E. On the Forced Electro-Magnetic Oscillations on Spherical Resonators. Philos. Mag. 1948, 39, 633–644. [Google Scholar] [CrossRef]
- Schumann, W.O. Über Die Strahlungslosen Eigenschwingungen Einer Leitenden Kugel, Die von Einer Luftschicht Und Einer Ionosphärenhülle Umgeben Ist. Z. Für Naturforsch. A 1952, 7, 149–154. [Google Scholar] [CrossRef]
- Schumann, W.O. Über Die Dämpfung Der Elektromagnetischen Eigenschwingungen Des Systems Erde—Luft—Ionosphäre. Z. Für Naturforsch. A 1952, 7, 250–252. [Google Scholar] [CrossRef]
- Schumann, W.O. Über die Ausbreitung sehr langer elektrischer Wellen um die Erde und die Signale des Blitzes. Il Nuovo Cimento 1952, 9, 1116–1138. [Google Scholar] [CrossRef]
- Schumann, W.O. Über die Ausbreitung sehr langer elektrischer Wellen und das Wellenspektrum der Blitzentladung. Naturwissenschaften 1952, 39, 475–476. [Google Scholar] [CrossRef]
- Schumann, W.O. Über Die Ausbreitung Sehr Langer Elektrischer Wellen Und Der Blitzentladung Um Die Erde. Z. Angew. Phys. 1952, 4, 474–480. [Google Scholar]
- Schumann, W.O. Über Die Oberwellenfelder Bei Der Ausbreitung Langer Elektrischer Wellen Um Die Erde Und Die Signale Des Blitzes. Naturwissenschaften 1953, 40, 504–505. [Google Scholar] [CrossRef]
- Schumann, W.O. Über Die Ausbreitung Langer Elektrischer Wellen Um Die Erde Und Einige Anwendungen Auf Senderinterferenzen Und Blitzsignale. Z. Angew. Phys. 1954, 6, 346. [Google Scholar]
- Schumann, W.O. Elektrische Eigenschwingnugen Des Systems Erde-Luft-Ionosphare. Z. Angew. Phys. 1957, 9, 373–378. [Google Scholar]
- Coroniti, S.C.; Hughes, J. Planetary Electrodynamics, the Chapter by Charles Polk; Gordon and Breach Science Publishers Inc: New York, NY, USA, 1969. [Google Scholar]
- Lysak, R.L. Feedback Instability of the Ionospheric Resonant Cavity. J. Geophys. Res. Space Phys. 1991, 96, 1553–1568. [Google Scholar] [CrossRef]
- Balser, M.; Wagner, C.A. Diurnal Power Variations of the Earth-Ionosphere Cavity Modes and Their Relationship to Worldwide Thunderstorm Activity. J. Geophys. Res. 1962, 67, 619–625. [Google Scholar] [CrossRef]
- Egerton, R.F. Electron Energy-Loss Spectroscopy in the TEM. Rep. Prog. Phys. 2009, 72, 016502. [Google Scholar] [CrossRef]
- Madden, T.; Thompson, W. Low-Frequency Electromagnetic Oscillations of the Earth-Ionosphere Cavity. Rev. Geophys. 1965, 3, 211. [Google Scholar] [CrossRef] [Green Version]
- Greifinger, C.; Greifinger, P. Approximate Method for Determining ELF Eigenvalues in the Earth-Ionosphere Waveguide. Radio Sci. 1978, 13, 831–837. [Google Scholar] [CrossRef]
- Mushtak, V.C.; Williams, E.R. ELF Propagation Parameters for Uniform Models of the Earth–Ionosphere Waveguide. J. Atmos. Sol.-Terr. Phys. 2002, 64, 1989–2001. [Google Scholar] [CrossRef]
- Williams, E.R.; Mushtak, V.C.; Nickolaenko, A.P. Distinguishing Ionospheric Models Using Schumann Resonance Spectra. J. Geophys. Res. 2006, 111, D16107. [Google Scholar] [CrossRef] [Green Version]
- Pechony, O.; Price, C.; Nickolaenko, A.P. Relative Importance of the Day-Night Asymmetry in Schumann Resonance Amplitude Records: Relative Importance of Day-Night Asymmetry. Radio Sci. 2007, 42, 1–12. [Google Scholar] [CrossRef] [Green Version]
- Zhou, H.; Yu, H.; Cao, B.; Qiao, X. Diurnal and Seasonal Variations in the Schumann Resonance Parameters Observed at Chinese Observatories. J. Atmos. Sol.-Terr. Phys. 2013, 98, 86–96. [Google Scholar] [CrossRef]
- Ouyang, X.Y.; Zhang, X.M.; Shen, X.H.; Miao, Y.Q. Background features of Schumann resonance observed in Yunnan, southwestern China. J. Geophys. 2013, 56, 1937–1944. (In Chinese) [Google Scholar] [CrossRef]
- Yin, F.; Zhang, Q.L.; Ji, T.T.; Jiang, S. Diurnal variations of Schumann resonances signals in the Earth-ionosphere cavity. J. Meteorol. Sci. 2015, 35, 480–487. (In Chinese) [Google Scholar] [CrossRef]
- Nickolaenko, A.P.; Schekotov, A.Y.; Hayakawa, M.; Romero, R.; Izutsu, J. Electromagnetic Manifestations of Tonga Eruption in Schumann Resonance Band. J. Atmos. Sol.-Terr. Phys. 2022, 237, 105897. [Google Scholar] [CrossRef]
- Bór, J.; Bozóki, T.; Sátori, G.; Williams, E.; Behnke, S.A.; Rycroft, M.J.; Buzás, A.; Silva, H.G.; Kubicki, M.; Said, R.; et al. Responses of the AC/DC Global Electric Circuit to Volcanic Electrical Activity in the Hunga Tonga-Hunga Ha’apai Eruption on 15 January 2022. J. Geophys. Res. Atmos. 2023, 128, e2022JD038238. [Google Scholar] [CrossRef]
- Nickolaenko, A.P.; Shvets, A.V.; Galuk, Y.P.; Schekotov, A.Y.; Hayakawa, M.; Mezentsev, A.; Romero, R.; De Rosa, R.; Kudintseva, I.G. Power Flux in the Schumann Resonance Band Linked to the Eruption of Tonga Volcano on Jan. 15, 2022. (Two Point Measurements of Umov-Poynting Vector). J. Atmos. Sol.-Terr. Phys. 2023, 247, 106078. [Google Scholar] [CrossRef]
- Izvekova, Y.N.; Popel, S.I.; Izvekov, O.Y. Dust and Dusty Plasma Effects in Schumann Resonances on Mars: Comparison with Earth. Icarus 2022, 371, 114717. [Google Scholar] [CrossRef]
- Mezentsev, A.; Nickolaenko, A.P.; Shvets, A.V.; Galuk, Y.P.; Schekotov, A.Y.; Hayakawa, M.; Romero, R.; Izutsu, J.; Kudintseva, I.G. Observational and Model Impact of Tonga Volcano Eruption on Schumann Resonance. J. Geophys. Res. Atmos. 2023, 128, e2022JD037841. [Google Scholar] [CrossRef]
- Gavrilov, B.G.; Poklad, Y.V.; Ryakhovsky, I.A.; Ermak, V.M.; Achkasov, N.S.; Kozakova, E.N. Global Electromagnetic Disturbances Caused by the Eruption of the Tonga Volcano on 15 January 2022. J. Geophys. Res. Atmos. 2022, 127, e2022JD037411. [Google Scholar] [CrossRef]
- Kong, Q.; Li, C.; Shi, K.; Guo, J.; Han, J.; Wang, T.; Bai, Q.; Chen, Y. Global Ionospheric Disturbance Propagation and Vertical Ionospheric Oscillation Triggered by the 2022 Tonga Volcanic Eruption. Atmosphere 2022, 13, 1697. [Google Scholar] [CrossRef]
- Price, C. ELF Electromagnetic Waves from Lightning: The Schumann Resonances. Atmosphere 2016, 7, 116. [Google Scholar] [CrossRef] [Green Version]
- Perotoni, M.B. Eigenmode Prediction of the Schumann Resonances. IEEE Antennas Wirel. Propag. Lett. 2018, 17, 942–945. [Google Scholar] [CrossRef]
- Ni, B.B.; Zhao, Z.Y. Spatial observations of Schumann resonance at the ionospheric altitudes. Chin. J. Geophys. 2005, 48, 744–750. (In Chinese) [Google Scholar] [CrossRef]
- Besser, B.P. Synopsis of the Historical Development of Schumann Resonances: History of Schumann Resonances. Radio Sci. 2007, 42, 1–20. [Google Scholar] [CrossRef]
- Balser, M.; Wagner, C.A. Observations of Earth–Ionosphere Cavity Resonances. Nature 1960, 188, 638–641. [Google Scholar] [CrossRef]
- Ohta, K.; Izutsu, J.; Hayakawa, M. Anomalous Excitation of Schumann Resonances and Additional Anomalous Resonances before the 2004 Mid-Niigata Prefecture Earthquake and the 2007 Noto Hantou Earthquake. Phys. Chem. Earth Parts ABC 2009, 34, 441–448. [Google Scholar] [CrossRef]
- Votis, C.I.; Tatsis, G.; Christofilakis, V.; Chronopoulos, S.K.; Kostarakis, P.; Tritakis, V.; Repapis, C. A New Portable ELF Schumann Resonance Receiver: Design and Detailed Analysis of the Antenna and the Analog Front-End. EURASIP J. Wirel. Commun. Netw. 2018, 2018, 155. [Google Scholar] [CrossRef] [Green Version]
- Cano-Domingo, C.; Castellano, N.N.; Fernandez-Ros, M.; Gazquez-Parra, J.A. Segmentation and Characteristic Extraction for Schumann Resonance Transient Events. Measurement 2022, 194, 110957. [Google Scholar] [CrossRef]
- Tatsis, G.; Christofilakis, V.; Chronopoulos, S.K.; Kostarakis, P.; Nistazakis, H.E.; Repapis, C.; Tritakis, V. Design and Implementation of a Test Fixture for ELF Schumann Resonance Magnetic Antenna Receiver and Magnetic Permeability Measurements. Electronics 2020, 9, 171. [Google Scholar] [CrossRef] [Green Version]
- Coughlin, M.W.; Cirone, A.; Meyers, P.; Atsuta, S.; Boschi, V.; Chincarini, A.; Christensen, N.L.; De Rosa, R.; Effler, A.; Fiori, I.; et al. Measurement and Subtraction of Schumann Resonances at Gravitational-Wave Interferometers. Phys. Rev. D 2018, 97, 102007. [Google Scholar] [CrossRef] [Green Version]
- Silagadze, Z.K. Schumann Resonance Transients and the Search for Gravitational Waves. Mod. Phys. Lett. A 2018, 33, 1850023. [Google Scholar] [CrossRef] [Green Version]
- Fan, Y.; Tang, J.; Zhao, G.Z.; Wang, L.F.; Wu, J.X.; Li, X.S.; Huang, T.B.; Liu, G.K. Schumann resonances variation observed from Electromagnetic monitoring stations. J. Geophys. 2013, 56, 2369–2377. [Google Scholar] [CrossRef]
- Cao, B.X.; Qiao, X.L. Schumann resonance observations in Low ionosphere. J. Electron. Inf. Technol. 2010, 32, 2002–2005. [Google Scholar] [CrossRef]
- Rodríguez-Camacho, J.; Fornieles, J.; Carrión, M.C.; Portí, J.A.; Toledo-Redondo, S.; Salinas, A. On the Need of a Unified Methodology for Processing Schumann Resonance Measurements. J. Geophys. Res. Atmos. 2018, 123, 13277–13290. [Google Scholar] [CrossRef]
- Soler-Ortiz, M.; Ros, M.F.; Castellano, N.N.; Parra, J.A.G. A New Way of Analyzing the Schumann Resonances: A Statistical Approach. IEEE Trans. Instrum. Meas. 2021, 70, 9508811. [Google Scholar] [CrossRef]
- Salinas, A.; Rodríguez-Camacho, J.; Portí, J.; Carrión, M.C.; Fornieles-Callejón, J.; Toledo-Redondo, S. Schumann Resonance Data Processing Programs and Four-Year Measurements from Sierra Nevada ELF Station. Comput. Geosci. 2022, 165, 105148. [Google Scholar] [CrossRef]
- Ogawa, T.; Kozai, K.; Kawamoto, H. Shumann Resonances Observed with a Balloon in the Stratosphere. J. Atmos. Terr. Phys. 1979, 41, 135–142. [Google Scholar] [CrossRef]
- Zhao, Z.Y.; Xie, S.G.; Masson, A.; Lefeuvre, F. Detection of Schumann Resonance in the Ionosphere F Region. Chin. J. Space Sci. 2000, 20, 113–120. [Google Scholar] [CrossRef]
- Simões, F.; Pfaff, R.; Freudenreich, H. Satellite Observations of Schumann Resonances in the Earth’s Ionosphere: Schumann Resonances in the Ionosphere. Geophys. Res. Lett. 2011, 38, L22101. [Google Scholar] [CrossRef]
- Dudkin, D.; Pilipenko, V.; Korepanov, V.; Klimov, S.; Holzworth, R. Electric Field Signatures of the IAR and Schumann Resonance in the Upper Ionosphere Detected by Chibis-M Microsatellite. J. Atmos. Sol.-Terr. Phys. 2014, 117, 81–87. [Google Scholar] [CrossRef]
- Toledo-Redondo, S.; Parrot, M.; Salinas, A. Variation of the First Cut-off Frequency of the Earth-Ionosphere Waveguide Observed by Demeter: Cut-off Frequency Observed by Demeter. J. Geophys. Res. Space Phys. 2012, 117, A04321. [Google Scholar] [CrossRef] [Green Version]
- Nickolaenko, A.P.; Rabinowicz, L.M. Study of the Annual Changes of Global Lightning Distribution and Frequency Variations of the First Schumann Resonance Mode. J. Atmos. Terr. Phys. 1995, 57, 1345–1348. [Google Scholar] [CrossRef]
- Tatsis, G.; Sakkas, A.; Christofilakis, V.; Baldoumas, G.; Chronopoulos, S.K.; Paschalidou, A.K.; Kassomenos, P.; Petrou, I.; Kostarakis, P.; Repapis, C.; et al. Correlation of Local Lightning Activity with Extra Low Frequency Detector for Schumann Resonance Measurements. Sci. Total Environ. 2021, 787, 147671. [Google Scholar] [CrossRef]
- Koloskov, A.V.; Nickolaenko, A.P.; Yampolsky, Y.M.; Hall, C.; Budanov, O.V. Variations of Global Thunderstorm Activity Derived from the Long-Term Schumann Resonance Monitoring in the Antarctic and in the Arctic. J. Atmos. Sol.-Terr. Phys. 2020, 201, 105231. [Google Scholar] [CrossRef]
- Price, C.; Melnikov, A. Diurnal, Seasonal and Inter-Annual Variations in the Schumann Resonance Parameters. J. Atmos. Sol.-Terr. Phys. 2004, 66, 1179–1185. [Google Scholar] [CrossRef]
- Ghosh, A.; Biswas, D.; Hazra, P.; Guha, G.; De, S.S. Studies on Schumann Resonance Phenomena and Some Recent Advancements. Geomagn. Aeron. 2019, 59, 980–994. [Google Scholar] [CrossRef]
- Shvets, A.V.; Hobara, Y.; Hayakawa, M. Variations of the Global Lightning Distribution Revealed from Three-Station Schumann Resonance Measurements: Global Lightning Distributions at ELF. J. Geophys. Res. Space Phys. 2010, 115, A12316. [Google Scholar] [CrossRef] [Green Version]
- Yamashita, K.; Takahashi, Y.; Sato, M.; Kase, H. Improvement in Lightning Geolocation by Time-of-Arrival Method Using Global ELF Network Data: Time-of-Arrival Method. J. Geophys. Res. Space Phys. 2011, 116, A00E61. [Google Scholar] [CrossRef]
- Prácser, E.; Bozóki, T.; Sátori, G.; Williams, E.; Guha, A.; Yu, H. Reconstruction of Global Lightning Activity Based on Schumann Resonance Measurements: Model Description and Synthetic Tests. Radio Sci. 2019, 54, 254–267. [Google Scholar] [CrossRef]
- Boldi, R.; Williams, E.; Guha, A. Determination of the Global-Average Charge Moment of a Lightning Flash Using Schumann Resonances and the LIS/OTD Lightning Data. J. Geophys. Res. Atmos. 2018, 123, 108–123. [Google Scholar] [CrossRef] [Green Version]
- Williams, E.; Mareev, E. Recent Progress on the Global Electrical Circuit. Atmos. Res. 2014, 135–136, 208–227. [Google Scholar] [CrossRef]
- Zhu, R.P.; Yuan, T.; Li, W.L.; Na, G.W. Characteristics of global lightning activities based on satellite observations. Clim. Environ. Res. 2013, 18, 639–650. (In Chinese) [Google Scholar] [CrossRef]
- Cecil, D.J.; Buechler, D.E.; Blakeslee, R.J. Gridded Lightning Climatology from TRMM-LIS and OTD: Dataset Description. Atmos. Res. 2014, 135–136, 404–414. [Google Scholar] [CrossRef] [Green Version]
- Ni, X.; Hui, W.; Zhang, Q.; Huang, F.; Liu, C. Comparison of Lightning Detection Between the FY-4A Lightning Mapping Imager and the ISS Lightning Imaging Sensor. Earth Space Sci. 2021, 8, e2020EA001099. [Google Scholar] [CrossRef]
- Rodger, C.J.; Werner, S.; Brundell, J.B.; Lay, E.H.; Thomson, N.R.; Holzworth, R.H.; Dowden, R.L. Detection Efficiency of the VLF World-Wide Lightning Location Network (WWLLN): Initial Case Study. Ann. Geophys. 2006, 24, 3197–3214. [Google Scholar] [CrossRef] [Green Version]
- Huang, E.; Williams, E.; Boldi, R.; Heckman, S.; Lyons, W.; Taylor, M.; Nelson, T.; Wong, C. Criteria for Sprites and Elves Based on Schumann Resonance Observations. J. Geophys. Res. Atmos. 1999, 104, 16943–16964. [Google Scholar] [CrossRef]
- Hayakawa, M.; Hobara, Y.; Suzuki, T. Lightning Effects in the Mesosphere and Ionosphere. Light. Electromagn. 2012, 16, 611–646. [Google Scholar] [CrossRef]
- Chern, J.L.; Hsu, R.R.; Su, H.T.; Mende, S.B.; Fukunishi, H.; Takahashi, Y.; Lee, L.C. Global Survey of Upper Atmospheric Transient Luminous Events on the ROCSAT-2 Satellite. J. Atmos. Sol.-Terr. Phys. 2003, 65, 647–659. [Google Scholar] [CrossRef]
- Neubert, T.; Allin, T.H.; Blanc, E.; Farges, T.; Haldoupis, C.; Mika, A.; Soula, S.; Knutsson, L.; van der Velde, O.; Marshall, R.A.; et al. Co-Ordinated Observations of Transient Luminous Events during the EuroSprite2003 Campaign. J. Atmos. Sol.-Terr. Phys. 2005, 67, 807–820. [Google Scholar] [CrossRef]
- Yair, Y.; Price, C.; Levin, Z.; Joseph, J.; Israelevitch, P.; Devir, A.; Moalem, M.; Ziv, B.; Asfur, M. Sprite Observations from the Space Shuttle during the Mediterranean Israeli Dust Experiment (MEIDEX). J. Atmos. Sol.-Terr. Phys. 2003, 65, 635–642. [Google Scholar] [CrossRef]
- Yair, Y.; Price, C.; Ganot, M.; Greenberg, E.; Yaniv, R.; Ziv, B.; Sherez, Y.; Devir, A.; Bór, J.; Sátori, G. Optical Observations of Transient Luminous Events Associated with Winter Thunderstorms near the Coast of Israel. Atmos. Res. 2009, 91, 529–537. [Google Scholar] [CrossRef]
- Nickolaenko, A.P.; Hayakawa, M.; Hobara, Y. Q-Bursts: Natural ELF Radio Transients. Surv. Geophys. 2010, 31, 409–425. [Google Scholar] [CrossRef]
- Ogawa, T.; Komatsu, M. Q-Bursts from Various Distances on the Earth. Atmos. Res. 2009, 91, 538–545. [Google Scholar] [CrossRef]
- Ogawa, T.; Komatsu, M. Propagation Velocity of VLF EM Waves from Lightning Discharges Producing Q-Bursts Observed in the Range 10–15Mm. Atmos. Res. 2010, 95, 101–107. [Google Scholar] [CrossRef]
- Bór, J.; Ludván, B.; Attila, N.; Steinbach, P. Systematic Deviations in Source Direction Estimates of Q-Bursts Recorded at Nagycenk, Hungary: On Deviations of ELF Source Directions. J. Geophys. Res. Atmos. 2016, 121, 5601–5619. [Google Scholar] [CrossRef] [Green Version]
- Yair, Y.; Fischer, G.; Simões, F.; Renno, N.; Zarka, P. Updated Review of Planetary Atmospheric Electricity. Space Sci. Rev. 2008, 137, 29–49. [Google Scholar] [CrossRef]
- Pechony, O.; Price, C. Schumann Resonance Parameters Calculated with a Partially Uniform Knee Model on Earth, Venus, Mars, and Titan: Schumann Resonance Model. Radio Sci. 2004, 39, 1–10. [Google Scholar] [CrossRef]
- Yang, H.; Pasko, V.P.; Yair, Y. Three-Dimensional Finite Difference Time Domain Modeling of the Schumann Resonance Parameters on Titan, Venus, and Mars: Schumann Resonances on Titan, Venus, and Mars. Radio Sci. 2006, 41, 1–10. [Google Scholar] [CrossRef]
- Béghin, C.; Canu, P.; Karkoschka, E.; Sotin, C.; Bertucci, C.; Kurth, W.S.; Berthelier, J.J.; Grard, R.; Hamelin, M.; Schwingenschuh, K.; et al. New Insights on Titan’s Plasma-Driven Schumann Resonance Inferred from Huygens and Cassini Data. Planet. Space Sci. 2009, 57, 1872–1888. [Google Scholar] [CrossRef]
- Béghin, C.; Randriamboarison, O.; Hamelin, M.; Karkoschka, E.; Sotin, C.; Whitten, R.C.; Berthelier, J.-J.; Grard, R.; Simões, F. Analytic Theory of Titan’s Schumann Resonance: Constraints on Ionospheric Conductivity and Buried Water Ocean. Icarus 2012, 218, 1028–1042. [Google Scholar] [CrossRef] [Green Version]
- Cano Domingo, C.; Fernandez Ros, M.; Novas Castellano, N.; Parra, J.A.G. Diurnal and Seasonal Results of the Schumann Resonance Observatory in Sierra De Filabres, Spain. IEEE Trans. Antennas Propag. 2021, 69, 6680–6690. [Google Scholar] [CrossRef]
- Domingo, C.C.; Castellano, N.N.; Stoean, R.; Fernandez-Ros, M.; Gazquez Parra, J.A. Schumann Resonance Modes and Ionosphere Parameters: An Annual Variability Comparison. IEEE Trans. Instrum. Meas. 2022, 71, 6005410. [Google Scholar] [CrossRef]
- Cano-Domingo, C.; Stoean, R.; Joya, G.; Novas, N.; Fernandez-Ros, M.; Gazquez, J.A. A Machine Learning Hourly Analysis on the Relation the Ionosphere and Schumann Resonance Frequency. Measurement 2023, 208, 112426. [Google Scholar] [CrossRef]
- Kulak, A. Solar Variations in Extremely Low Frequency Propagation Parameters: 1. A Two-Dimensional Telegraph Equation (TDTE) Model of ELF Propagation and Fundamental Parameters of Schumann Resonances. J. Geophys. Res. 2003, 108, 1270. [Google Scholar] [CrossRef]
- Kulak, A. Solar Variations in Extremely Low Frequency Propagation Parameters: 2. Observations of Schumann Resonances and Computation of the ELF Attenuation Parameter. J. Geophys. Res. 2003, 108, 1271. [Google Scholar] [CrossRef]
- Sátori, G.; Williams, E.; Price, C.; Boldi, R.; Koloskov, A.; Yampolski, Y.; Guha, A.; Barta, V. Effects of Energetic Solar Emissions on the Earth–Ionosphere Cavity of Schumann Resonances. Surv. Geophys. 2016, 37, 757–789. [Google Scholar] [CrossRef] [Green Version]
- Bozóki, T.; Sátori, G.; Williams, E.; Mironova, I.; Steinbach, P.; Bland, E.C.; Koloskov, A.; Yampolski, Y.M.; Budanov, O.V.; Neska, M.; et al. Solar Cycle-Modulated Deformation of the Earth–Ionosphere Cavity. Front. Earth Sci. 2021, 9, 689127. [Google Scholar] [CrossRef]
- Kudintseva, I.G.; Galuk, Y.P.; Nickolaenko, A.P.; Hayakawa, M. Modifications of Middle Atmosphere Conductivity during Sudden Ionospheric Disturbances Deduced from Changes of Schumann Resonance Peak Frequencies. Radio Sci. 2018, 53, 670–682. [Google Scholar] [CrossRef]
- Beggan, C.D.; Musur, M. Observation of Ionospheric Alfvén Resonances at 1–30 Hz and Their Superposition with the Schumann Resonances. J. Geophys. Res. Space Phys. 2018, 123, 4202–4214. [Google Scholar] [CrossRef] [Green Version]
- Pazos, M.; Mendoza, B.; Sierra, P.; Andrade, E.; Rodríguez, D.; Mendoza, V.; Garduño, R. Analysis of the Effects of Geomagnetic Storms in the Schumann Resonance Station Data in Mexico. J. Atmos. Sol.-Terr. Phys. 2019, 193, 105091. [Google Scholar] [CrossRef]
- Hayakawa, M.; Hobara, Y.; Ohta, K.; Izutsu, J.; Nickolaenko, A.P.; Sorokin, V. Seismogenic Effects in the ELF Schumann Resonance Band. IEEJ Trans. Fundam. Mater. 2011, 131, 684–690. [Google Scholar] [CrossRef]
- Schekotov, A.Y.; Molchanov, O.A.; Hayakawa, M.; Fedorov, E.N.; Chebrov, V.N.; Sinitsin, V.I.; Gordeev, E.E.; Belyaev, G.G.; Yagova, N.V. ULF/ELF Magnetic Field Variations from Atmosphere Induced by Seismicity: ULF/ELF Electromagnetic Emission. Radio Sci. 2007, 42, 1–13. [Google Scholar] [CrossRef]
- Molchanov, O.A.; Hayakawa, M. Seismo-Electromagnetics and Related Phenomena: History and Latest Results; Terrapub: Tokyo, Japan, 2008. [Google Scholar]
- Ohta, K.; Watanabe, N.; Hayakawa, M. Survey of Anomalous Schumann Resonance Phenomena Observed in Japan, in Possible Association with Earthquakes in Taiwan. Phys. Chem. Earth Parts ABC 2006, 31, 397–402. [Google Scholar] [CrossRef]
- De, S.S.; De, B.K.; Bandyopadhyay, B.; Paul, S.; Haldar, D.K.; Barui, S. Studies on the Shift in the Frequency of the First Schumann Resonance Mode during a Solar Proton Event. J. Atmos. Sol.-Terr. Phys. 2010, 72, 829–836. [Google Scholar] [CrossRef]
- Hayakawa, M.; Ohta, K.; Nickolaenko, A.P.; Ando, Y. Anomalous Effect in Schumann Resonance Phenomena Observed in Japan, Possibly Associated with the Chi-Chi Earthquake in Taiwan. Ann. Geophys. 2005, 23, 1335–1346. [Google Scholar] [CrossRef] [Green Version]
- Hayakawa, M.; Nickolaenko, A.P.; Sekiguchi, M.; Yamashita, K.; Ida, Y.; Yano, M. Anomalous ELF Phenomena in the Schumann Resonance Band as Observed at Moshiri (Japan) in Possible Association with an Earthquake in Taiwan. Nat. Hazards Earth Syst. Sci. 2008, 8, 1309–1316. [Google Scholar] [CrossRef]
- Nickolaenko, A.P.; Galuk, Y.P.; Hayakawa, M. The Effect of a Compact Ionosphere Disturbance over the Earthquake: A Focus on Schumann Resonance. Int. J. Electron. Appl. Res. 2018, 5, 11–39. [Google Scholar] [CrossRef]
- Christofilakis, V.; Tatsis, G.; Votis, C.; Contopoulos, I.; Repapis, C.; Tritakis, V. Significant ELF Perturbations in the Schumann Resonance Band before and during a Shallow Mid-Magnitude Seismic Activity in the Greek Area (Kalpaki). J. Atmos. Sol.-Terr. Phys. 2019, 182, 138–146. [Google Scholar] [CrossRef]
- Galuk, Y.P.; Kudintseva, I.G.; Nickolaenko, A.P.; Hayakawa, M. Modifications of Schumann Resonance Spectra as an Estimate of Causative Earthquake Magnitude: The Model Treatment. J. Atmos. Sol.-Terr. Phys. 2020, 209, 105392. [Google Scholar] [CrossRef]
- Sierra Figueredo, P.; Mendoza Ortega, B.; Pazos, M.; Rodríguez Osorio, D.; Andrade Mascote, E.; Mendoza, V.M.; Garduño, R. Schumann Resonance Anomalies Possibly Associated with Large Earthquakes in Mexico. Indian J. Phys. 2021, 95, 1959–1966. [Google Scholar] [CrossRef]
- Tritakis, V.; Contopoulos, I.; Mlynarczyk, J.; Christofilakis, V.; Tatsis, G.; Repapis, C. How Effective and Prerequisite Are Electromagnetic Extremely Low Frequency (ELF) Recordings in the Schumann Resonances Band to Function as Seismic Activity Precursors. Atmosphere 2022, 13, 185. [Google Scholar] [CrossRef]
- Hayakawa, M.; Izutsu, J.; Schekotov, A.Y.; Nickolaenko, A.P.; Galuk, Y.P.; Kudintseva, I.G. Anomalies of Schumann Resonances as Observed near Nagoya Associated with Two Huge (M~7) Tohoku Offshore Earthquakes in 2021. J. Atmos. Sol.-Terr. Phys. 2021, 225, 105761. [Google Scholar] [CrossRef]
- Zhou, H.; Zhou, Z.; Qiao, X.; Yu, H. Anomalous Phenomena in Schumann Resonance Band Observed in China before the 2011 Magnitude 9.0 Tohoku-Oki Earthquake in Japan: SR Anomalies before a Large Earthquake. J. Geophys. Res. Atmos. 2013, 118, 13338–13345. [Google Scholar] [CrossRef]
- Williams, E.R. The Schumann Resonance: A Global Tropical Thermometer. Science 1992, 256, 1184–1187. [Google Scholar] [CrossRef]
- Price, C.; Asfur, M. Can Lightning Observations Be Used as an Indicator of Upper-Tropospheric Water Vapor Variability? Bull. Am. Meteorol. Soc. 2006, 87, 291–298. [Google Scholar] [CrossRef]
- Sátori, G.; Williams, E.; Lemperger, I. Variability of Global Lightning Activity on the ENSO Time Scale. Atmos. Res. 2009, 91, 500–507. [Google Scholar] [CrossRef]
- Sátori, G.; Zieger, B. El Niňo Related Meridional Oscillation of Global Lightning Activity. Geophys. Res. Lett. 1999, 26, 1365–1368. [Google Scholar] [CrossRef]
- Wang, C.; Deser, C.; Yu, J.-Y.; DiNezio, P.; Clement, A. El Niño and Southern Oscillation (ENSO): A Review. In Coral Reefs of the Eastern Tropical Pacific; Glynn, P.W., Manzello, D.P., Enochs, I.C., Eds.; Coral Reefs of the World; Springer: Dordrecht, The Netherlands, 2017; Volume 8, pp. 85–106. ISBN 978-94-017-7498-7. [Google Scholar]
- Bozóki, T.; Williams, E.; Satori, G.; Beggan, C.D.; Price, C.; Steinbach, P.; Guha, A.; Liu, Y.; Neska, A.; Boldi, R.; et al. Predicting the Occurrence of Extreme El Nino Events Based on Schumann Resonancemeasurements? In Proceedings of the 24th EGU General Assembly, Vienna, Austria, 23–27 May 2022. [Google Scholar]
- Williams, E.; Bozóki, T.; Sátori, G.; Price, C.; Steinbach, P.; Guha, A.; Liu, Y.; Beggan, C.D.; Neska, M.; Boldi, R.; et al. Evolution of Global Lightning in the Transition from Cold to Warm Phase Preceding Two Super El Niño Events. J. Geophys. Res. Atmos. 2021, 126, e2020JD033526. [Google Scholar] [CrossRef]
- Beggan, C.D.; Musur, M.A. Is the Madden–Julian Oscillation Reliably Detectable in Schumann Resonances? J. Atmos. Sol.-Terr. Phys. 2019, 190, 108–116. [Google Scholar] [CrossRef] [Green Version]
- Kozlov, A.V.; Slyunyaev, N.N.; Ilin, N.V.; Sarafanov, F.G.; Frank-Kamenetsky, A.V. The Effect of the Madden–Julian Oscillation on the Global Electric Circuit. Atmos. Res. 2023, 284, 106585. [Google Scholar] [CrossRef]
- Balser, M.; Wagner, C.A. Effect of a High-Altitude Nuclear Detonation on the Earth-Ionosphere Cavity. J. Geophys. Res. 1963, 68, 4115–4118. [Google Scholar] [CrossRef]
- Wait, J. Historical Background and Introduction to the Special Issue on Extremely Low Frequency (ELF) Communications. IEEE Trans. Commun. 1974, 22, 353–354. [Google Scholar] [CrossRef]
- Wait, J. Propagation of ELF Electromagnetic Waves and Project Sanguine/Seafarer. IEEE J. Ocean. Eng. 1977, 2, 161–172. [Google Scholar] [CrossRef]
- Cherry, N.J. Human Intelligence: The Brain, an Electromagnetic System Synchronised by the Schumann Resonance Signal. Med. Hypotheses 2003, 60, 843–844. [Google Scholar] [CrossRef] [Green Version]
- Cherry, N. Schumann Resonances, a Plausible Biophysical Mechanism for the Human Health Effects of Solar. Nat. Hazards 2002, 26, 279–331. [Google Scholar] [CrossRef]
- Danho, S.; Schoellhorn, W.; Aclan, M. Innovative Technical Implementation of the Schumann Resonances and Its Influence on Organisms and Biological Cells. IOP Conf. Ser. Mater. Sci. Eng. 2019, 564, 012081. [Google Scholar] [CrossRef]
- Elhalel, G.; Price, C.; Fixler, D.; Shainberg, A. Cardioprotection from Stress Conditions by Weak Magnetic Fields in the Schumann Resonance Band. Sci. Rep. 2019, 9, 1645. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Fdez-Arroyabe, P.; Fornieles-Callejón, J.; Santurtún, A.; Szangolies, L.; Donner, R.V. Schumann Resonance and Cardiovascular Hospital Admission in the Area of Granada, Spain: An Event Coincidence Analysis Approach. Sci. Total Environ. 2020, 705, 135813. [Google Scholar] [CrossRef] [PubMed]
- Fdez-Arroyabe, P.; Kourtidis, K.; Haldoupis, C.; Savoska, S.; Matthews, J.; Mir, L.M.; Kassomenos, P.; Cifra, M.; Barbosa, S.; Chen, X.; et al. Glossary on Atmospheric Electricity and Its Effects on Biology. Int. J. Biometeorol. 2021, 65, 5–29. [Google Scholar] [CrossRef]
- Hunting, E.R.; Matthews, J.; De Arróyabe Hernáez, P.F.; England, S.J.; Kourtidis, K.; Koh, K.; Nicoll, K.; Harrison, R.G.; Manser, K.; Price, C.; et al. Challenges in Coupling Atmospheric Electricity with Biological Systems. Int. J. Biometeorol. 2021, 65, 45–58. [Google Scholar] [CrossRef]
- Price, C.; Williams, E.; Elhalel, G.; Sentman, D. Natural ELF Fields in the Atmosphere and in Living Organisms. Int. J. Biometeorol. 2021, 65, 85–92. [Google Scholar] [CrossRef]
- Sukhov, V.; Sukhova, E.; Sinitsyna, Y.; Gromova, E.; Mshenskaya, N.; Ryabkova, A.; Ilin, N.; Vodeneev, V.; Mareev, E.; Price, C. Influence of Magnetic Field with Schumann Resonance Frequencies on Photosynthetic Light Reactions in Wheat and Pea. Cells 2021, 10, 149. [Google Scholar] [CrossRef]
- Huang, J.; Shen, X.; Zhang, X.; Lu, H.; Tan, Q.; Wang, Q.; Yan, R.; Chu, W.; Yang, Y.; Liu, D.; et al. Application System and Data Description of the China Seismo-Electromagnetic Satellite. Earth Planet. Phys. 2018, 2, 444–454. [Google Scholar] [CrossRef]
- Wang, L.W.; Hu, Z.; Shen, X.H.; Zhang, X.G.; Huang, J.P.; Zhang, Y.; Yang, Y.Y. Data processing methods and procedures of CSES satellite. J. Remote Sens. 2018, 22 (Suppl. S1), 39–55. (In Chinese) [Google Scholar] [CrossRef]
- Shen, X.H.; Zhang, X.M.; Cui, J.; Zhou, X.; Jiang, W.L.; Gong, L.X.; Li, Y.S.; Liu, Q.Q. Remote sensing application in earthquake science research and geophysical fields exploration satellite mission in China. J. Remote Sens. 2018, 22 (Suppl. S1), 1–16. (In Chinese) [Google Scholar] [CrossRef]




Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, J.; Huang, J.; Li, Z.; Zhao, Z.; Zeren, Z.; Shen, X.; Wang, Q. Recent Advances and Challenges in Schumann Resonance Observations and Research. Remote Sens. 2023, 15, 3557. https://doi.org/10.3390/rs15143557
Liu J, Huang J, Li Z, Zhao Z, Zeren Z, Shen X, Wang Q. Recent Advances and Challenges in Schumann Resonance Observations and Research. Remote Sensing. 2023; 15(14):3557. https://doi.org/10.3390/rs15143557
Chicago/Turabian StyleLiu, Jinlai, Jianping Huang, Zhong Li, Zhengyu Zhao, Zhima Zeren, Xuhui Shen, and Qiao Wang. 2023. "Recent Advances and Challenges in Schumann Resonance Observations and Research" Remote Sensing 15, no. 14: 3557. https://doi.org/10.3390/rs15143557