Spatiotemporal Comparison of Drought in Shaanxi–Gansu–Ningxia from 2003 to 2020 Using Various Drought Indices in Google Earth Engine
Abstract
:1. Introduction
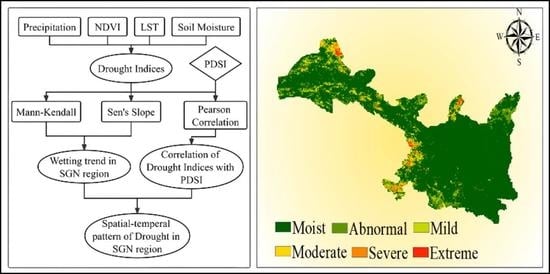
2. Materials and Methods
2.1. Study Area
2.2. Datasets and Pre-Processing
2.2.1. Precipitation Data
2.2.2. NDVI and LST Data
2.2.3. Soil Moisture Data
2.2.4. Other Data
2.3. Methods
2.3.1. SPI
2.3.2. VHI
2.3.3. NVSWI
2.3.4. SMADI
2.3.5. Trend Analysis
2.3.6. Assessment Criterion
2.3.7. Pearson Correlation Coefficient
3. Results
3.1. Temporal Comparisons
3.1.1. Time Series Comparisons
3.1.2. Trend Analysis Comparisons
3.2. Spatial Comparisons
3.3. Drought Assessment Comparisons
3.4. Correlation Comparisons
4. Discussion
4.1. Trends of Drought in SGN Area
4.2. Advantages of Comparing Various Drought Indices
4.3. Limitations
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Doughty, R.; Xiao, X.; Wu, X.; Zhang, Y.; Bajgain, R.; Zhou, Y.; Qin, Y.; Zou, Z.; McCarthy, H.; Friedman, J. Responses of gross primary production of grasslands and croplands under drought, pluvial, and irrigation conditions during 2010–2016, Oklahoma, USA. Agric. Water Manag. 2018, 204, 47–59. [Google Scholar]
- Li, Q.; Li, P.; Li, H.; Yu, M. Drought assessment using a multivariate drought index in the Luanhe River basin of Northern China. Stoch. Environ. Res. Risk Assess. 2015, 29, 1509–1520. [Google Scholar]
- Li, Q.; Zeng, M.; Wang, H.; Li, P.; Wang, K.; Yu, M. Drought assessment using a multivariate drought index in the Huaihe River basin of Eastern China. Proc. Int. Assoc. Hydrol. Sci. 2015, 369, 61–67. [Google Scholar]
- Wang, K.Y.; Li, Q.F.; Yang, Y.; Zeng, M.; Li, P.C.; Zhang, J.X. Analysis of spatio-temporal evolution of droughts in Luanhe River Basin using different drought indices. Water Sci. Eng. 2015, 8, 282–290. [Google Scholar]
- Zhang, L.; Jiao, W.; Zhang, H.; Huang, C.; Tong, Q. Studying drought phenomena in the Continental United States in 2011 and 2012 using various drought indices. Remote Sens. Environ. 2017, 190, 96–106. [Google Scholar]
- Keyantash, J.A.; Dracup, J.A. An aggregate drought index: Assessing drought severity based on fluctuations in the hydrologic cycle and surface water storage. Water Resour. Res. 2004, 40. [Google Scholar] [CrossRef] [Green Version]
- Wilhelmi, O.V.; Wilhite, D.A. Assessing vulnerability to agricultural drought: A Nebraska case study. Nat. Hazards 2002, 25, 37–58. [Google Scholar]
- Zhou, L.; Zhang, J.; Wu, J.; Zhao, L.; Liu, M.; Lü, A.; Wu, Z. Comparison of remotely sensed and meteorological data-derived drought indices in mid-eastern China. Int. J. Remote Sens. 2012, 33, 1755–1779. [Google Scholar]
- Quiring, S.M.; Papakryiakou, T.N. An evaluation of agricultural drought indices for the Canadian prairies. Agric. For. Meteorol. 2003, 118, 49–62. [Google Scholar]
- Dracup, J.A.; Lee, K.S.; Paulson, E.G., Jr. On the statistical characteristics of drought events. Water Resour. Res. 1980, 16, 289–296. [Google Scholar]
- Souza, A.G.S.S.; Neto, A.R.; de Souza, L.L. Soil moisture-based index for agricultural drought assessment: SMADI application in Pernambuco State-Brazil. Remote Sens. Environ. 2021, 252, 112124. [Google Scholar]
- Zhang, A.; Jia, G. Monitoring meteorological drought in semiarid regions using multi-sensor microwave remote sensing data. Remote Sens. Environ. 2013, 134, 12–23. [Google Scholar]
- Yao, J.; Zhao, Y.; Chen, Y.; Yu, X.; Zhang, R. Multi-scale assessments of droughts: A case study in Xinjiang, China. Sci. Total Environ. 2018, 630, 444–452. [Google Scholar] [PubMed]
- Xu, H.J.; Wang, X.P.; Zhao, C.Y.; Shan, S.Y.; Guo, J. Seasonal and aridity influences on the relationships between drought indices and hydrological variables over China. Weather. Clim. Extrem. 2021, 34, 100393. [Google Scholar]
- Ma, X.; Huete, A.; Cleverly, J.; Eamus, D.; Chevallier, F.; Joiner, J.; Poulter, B.; Zhang, Y.; Guanter, L.; Meyer, W. Drought rapidly diminishes the large net CO2 uptake in 2011 over semi-arid Australia. Sci. Rep. 2016, 6, 1–9. [Google Scholar]
- Xu, H.J.; Wang, X.P.; Zhao, C.Y. Drought sensitivity of vegetation photosynthesis along the aridity gradient in northern China. Int. J. Appl. Earth Obs. Geoinf. 2021, 102, 102418. [Google Scholar]
- Palmer, W.C. Meteorological Drought; US Department of Commerce, Weather Bureau: Washington, DC, USA, 1965; Volume 30.
- McKee, T.B.; Doesken, N.J.; Kleist, J. The relationship of drought frequency and duration to time scales. In Proceedings of the 8th Conference on Applied Climatology, Anaheim, CA, USA, 17–22 January 1993; pp. 179–183. [Google Scholar]
- Kogan, F.N. Droughts of the late 1980s in the United States as derived from NOAA polar-orbiting satellite data. Bull. Am. Meteorol. Soc. 1995, 76, 655–668. [Google Scholar]
- Kogan, F.N. Application of vegetation index and brightness temperature for drought detection. Adv. Space Res. 1995, 15, 91–100. [Google Scholar]
- Kogan, F. World droughts in the new millennium from AVHRR—Based vegetation health indices. Eos. Trans. Am. Geophys. Union 2002, 83, 557–563. [Google Scholar]
- Sandholt, I.; Rasmussen, K.; Andersen, J. A simple interpretation of the surface temperature/vegetation index space for assessment of surface moisture status. Remote Sens. Environ. 2002, 79, 213–224. [Google Scholar]
- Sadeghi, M.; Babaeian, E.; Tuller, M.; Jones, S.B. The optical trapezoid model: A novel approach to remote sensing of soil moisture applied to Sentinel-2 and Landsat-8 observations. Remote Sens. Environ. 2017, 198, 52–68. [Google Scholar]
- Zhao, X.; Xia, H.; Pan, L.; Song, H.; Niu, W.; Wang, R.; Li, R.; Bian, X.; Guo, Y.; Qin, Y. Drought monitoring over Yellow River basin from 2003–2019 using reconstructed MODIS land surface temperature in Google Earth Engine. Remote Sens. 2021, 13, 3748. [Google Scholar]
- Vicente-Serrano, S.M.; Beguería, S.; López-Moreno, J.I. A multiscalar drought index sensitive to global warming: The standardized precipitation evapotranspiration index. J. Clim. 2010, 23, 1696–1718. [Google Scholar]
- Rhee, J.; Im, J.; Carbone, G.J. Monitoring agricultural drought for arid and humid regions using multi-sensor remote sensing data. Remote Sens. Environ. 2010, 114, 2875–2887. [Google Scholar]
- Abbas, S.; Nichol, J.E.; Qamer, F.M.; Xu, J. Characterization of drought development through remote sensing: A case study in Central Yunnan, China. Remote Sens. 2014, 6, 4998–5018. [Google Scholar]
- Sánchez, N.; González-Zamora, Á.; Piles, M.; Martínez-Fernández, J. A new Soil Moisture Agricultural Drought Index (SMADI) integrating MODIS and SMOS products: A case of study over the Iberian Peninsula. Remote Sens. 2016, 8, 287. [Google Scholar]
- Trenberth, K.E.; Dai, A.; Van Der Schrier, G.; Jones, P.D.; Barichivich, J.; Briffa, K.R.; Sheffield, J. Global warming and changes in drought. Nat. Clim. Change 2014, 4, 17–22. [Google Scholar]
- Sheffield, J.; Wood, E.F.; Roderick, M.L. Little change in global drought over the past 60 years. Nature 2012, 491, 435–438. [Google Scholar]
- Dai, A. Increasing drought under global warming in observations and models. Nat. Clim. Change 2013, 3, 52–58. [Google Scholar]
- Wu, M.; Li, Y.; Hu, W.; Yao, N.; Li, L.; Liu, D.L. Spatiotemporal variability of standardized precipitation evapotranspiration index in mainland China over 1961–2016. Int. J. Climatol. 2020, 40, 4781–4799. [Google Scholar]
- Wang, Z.; Li, J.; Lai, C.; Zeng, Z.; Zhong, R.; Chen, X.; Zhou, X.; Wang, M. Does drought in China show a significant decreasing trend from 1961 to 2009? Sci. Total Environ. 2017, 579, 314–324. [Google Scholar]
- Yu, X.; He, X.; Zheng, H.; Guo, R.; Ren, Z.; Zhang, D.; Lin, J. Spatial and temporal analysis of drought risk during the crop-growing season over northeast China. Nat. Hazards 2014, 71, 275–289. [Google Scholar]
- Zhao, S.; Cong, D.; He, K.; Yang, H.; Qin, Z. Spatial-temporal variation of drought in China from 1982 to 2010 based on a modified temperature vegetation drought index (mTVDI). Sci. Rep. 2017, 7, 1–12. [Google Scholar]
- Huang, W.; Yang, X.; Li, M.; Zhang, X.; Wang, M.; Dai, S.; Ma, J. Evolution characteristics of seasonal drought in the south of China during the past 58 years based on standardized precipitation index. Trans. Chin. Soc. Agric. Eng. 2010, 26, 50–59. [Google Scholar]
- Zhu, Y.; Wang, W.; Singh, V.P.; Liu, Y. Combined use of meteorological drought indices at multi-time scales for improving hydrological drought detection. Sci. Total Environ. 2016, 571, 1058–1068. [Google Scholar]
- Mishra, D.; Goswami, S.; Matin, S.; Sarup, J. Analyzing the extent of drought in the Rajasthan state of India using vegetation condition index and standardized precipitation index. Modeling Earth Syst. Environ. 2022, 8, 601–610. [Google Scholar]
- Wei, W.; Zhang, J.; Zhou, L.; Xie, B.; Zhou, J.; Li, C. Comparative evaluation of drought indices for monitoring drought based on remote sensing data. Environ. Sci. Pollut. Res. 2021, 28, 20408–20425. [Google Scholar]
- Zhang, H.; Ali, S.; Ma, Q.; Sun, L.; Jiang, N.; Jia, Q.; Hou, F. Remote sensing strategies to characterization of drought, vegetation dynamics in relation to climate change from 1983 to 2016 in Tibet and Xinjiang Province, China. Environ. Sci. Pollut. Res. 2021, 28, 21085–21100. [Google Scholar]
- Ali, S.; Haixing, Z.; Qi, M.; Liang, S.; Ning, J.; Jia, Q.; Hou, F. Monitoring drought events and vegetation dynamics in relation to climate change over mainland China from 1983 to 2016. Environ. Sci. Pollut. Res. 2021, 28, 21910–21925. [Google Scholar]
- Salvia, M.; Sanchez, N.; Piles, M.; Ruscica, R.; Gonzalez-Zamora, A.; Roitberg, E.; Martinez-Fernandez, J. The added-value of remotely-sensed soil moisture data for agricultural drought detection in Argentina. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 6487–6500. [Google Scholar]
- Funk, C.; Peterson, P.; Landsfeld, M.; Pedreros, D.; Verdin, J.; Shukla, S.; Husak, G.; Rowland, J.; Harrison, L.; Hoell, A.; et al. The climate hazards infrared precipitation with stations—A new environmental record for monitoring extremes. Sci. Data 2015, 2, 150066. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhao, W.; He, J.; Yin, G.; Wen, F.; Wu, H. Spatiotemporal variability in land surface temperature over the mountainous region affected by the 2008 Wenchuan earthquake from 2000 to 2017. J. Geophys. Res. Atmos. 2019, 124, 1975–1991. [Google Scholar]
- Zhao, W.; Duan, S.-B. Reconstruction of daytime land surface temperatures under cloud-covered conditions using integrated MODIS/Terra land products and MSG geostationary satellite data. Remote Sens. Environ. 2020, 247, 111931. [Google Scholar]
- Pan, L.; Xia, H.; Zhao, X.; Guo, Y.; Qin, Y. Mapping winter crops using a phenology algorithm, time-series Sentinel-2 and Landsat-7/8 images, and Google Earth Engine. Remote Sens. 2021, 13, 2510. [Google Scholar]
- Guo, Y.; Xia, H.; Pan, L.; Zhao, X.; Li, R. Mapping the northern limit of double cropping using a phenology-based algorithm and Google Earth Engine. Remote Sens. 2022, 14, 1004. [Google Scholar]
- Li, W.; Perera, S.; Linstead, E.; Thomas, R.; El-Askary, H.; Piechota, T.; Struppa, D. Investigating decadal changes of multiple hydrological products and land-cover changes in the Mediterranean Region for 2009–2018. Earth Syst. Environ. 2021, 5, 285–302. [Google Scholar]
- McNally, A.; Arsenault, K.; Kumar, S.; Shukla, S.; Peterson, P.; Wang, S.; Funk, C.; Peters-Lidard, C.D.; Verdin, J.P. A land data assimilation system for sub-Saharan Africa food and water security applications. Sci. Data 2017, 4, 1–19. [Google Scholar]
- Abatzoglou, J.T.; Dobrowski, S.Z.; Parks, S.A.; Hegewisch, K.C. TerraClimate, a high-resolution global dataset of monthly climate and climatic water balance from 1958–2015. Sci. Data 2018, 5, 1–12. [Google Scholar]
- Zhao, G.; Gao, H. Estimating reservoir evaporation losses for the United States: Fusing remote sensing and modeling approaches. Remote Sens. Environ. 2019, 226, 109–124. [Google Scholar]
- Yang, J.; Dong, J.; Xiao, X.; Dai, J.; Wu, C.; Xia, J.; Zhao, G.; Zhao, M.; Li, Z.; Zhang, Y. Divergent shifts in peak photosynthesis timing of temperate and alpine grasslands in China. Remote Sens. Environ. 2019, 233, 111395. [Google Scholar]
- Fang, W.; Huang, S.; Huang, Q.; Huang, G.; Wang, H.; Leng, G.; Wang, L.; Guo, Y. Probabilistic assessment of remote sensing-based terrestrial vegetation vulnerability to drought stress of the Loess Plateau in China. Remote Sens. Environ. 2019, 232, 111290. [Google Scholar]
- Alami, M.M.; Hayat, E.; Tayfur, G. Proposing a popular method for meteorological drought monitoring in the Kabul River Basin, Afghanistan. Int. J. Adv. Eng. Res. Sci. 2017, 4, 237199. [Google Scholar]
- Alizadeh, M.R.; Nikoo, M.R. A fusion-based methodology for meteorological drought estimation using remote sensing data. Remote Sens. Environ. 2018, 211, 229–247. [Google Scholar]
- Javed, T.; Li, Y.; Rashid, S.; Li, F.; Hu, Q.; Feng, H.; Chen, X.; Ahmad, S.; Liu, F.; Pulatov, B. Performance and relationship of four different agricultural drought indices for drought monitoring in China’s mainland using remote sensing data. Sci. Total Environ. 2021, 759, 143530. [Google Scholar] [PubMed]
- Jiao, W.; Tian, C.; Chang, Q.; Novick, K.A.; Wang, L. A new multi-sensor integrated index for drought monitoring. Agric. For. Meteorol. 2019, 268, 74–85. [Google Scholar]
- Won, J.; Choi, J.; Lee, O.; Kim, S. Copula-based Joint Drought Index using SPI and EDDI and its application to climate change. Sci. Total Environ. 2020, 744, 140701. [Google Scholar]
- Lloyd-Hughes, B.; Saunders, M.A. A drought climatology for Europe. Int. J. Climatol. A J. R. Meteorol. Soc. 2002, 22, 1571–1592. [Google Scholar]
- Kogan, F.N. Operational space technology for global vegetation assessment. Bull. Am. Meteorol. Soc. 2001, 82, 1949–1964. [Google Scholar]
- Kogan, F.N. Global drought watch from space. Bull. Am. Meteorol. Soc. 1997, 78, 621–636. [Google Scholar]
- Liu, Q.; Zhang, J.; Zhang, H.; Yao, F.; Bai, Y.; Zhang, S.; Meng, X.; Liu, Q. Evaluating the performance of eight drought indices for capturing soil moisture dynamics in various vegetation regions over China. Sci. Total Environ. 2021, 789, 147803. [Google Scholar]
- Cong, D.; Zhao, S.; Chen, C.; Duan, Z. Characterization of droughts during 2001–2014 based on remote sensing: A case study of Northeast China. Ecol. Inform. 2017, 39, 56–67. [Google Scholar]
- Sánchez, N.; González-Zamora, Á.; Martínez-Fernández, J.; Piles, M.; Pablos, M. Integrated remote sensing approach to global agricultural drought monitoring. Agric. For. Meteorol. 2018, 259, 141–153. [Google Scholar]
- Carlson, T. An overview of the “triangle method” for estimating surface evapotranspiration and soil moisture from satellite imagery. Sensors 2007, 7, 1612–1629. [Google Scholar]
- Gocic, M.; Trajkovic, S. Analysis of changes in meteorological variables using Mann-Kendall and Sen’s slope estimator statistical tests in Serbia. Glob. Planet. Change 2013, 100, 172–182. [Google Scholar]
- Mann, H.B. Nonparametric tests against trend. Econom. J. Econom. Soc. 1945, 13, 245–259. [Google Scholar]
- Sen, P.K. Estimates of the regression coefficient based on Kendall’s tau. J. Am. Stat. Assoc. 1968, 63, 1379–1389. [Google Scholar]
- Ali, R.O.; Abubaker, S.R. Trend analysis using Mann-Kendall, Sen’s slope estimator test and innovative trend analysis method in Yangtze river basin, China. Int. J. Eng. Technol. 2019, 8, 110–119. [Google Scholar]
- Ali, R.; Kuriqi, A.; Abubaker, S.; Kisi, O. Long-term trends and seasonality detection of the observed flow in Yangtze River using Mann-Kendall and Sen’s innovative trend method. Water 2019, 11, 1855. [Google Scholar]
- Collaud Coen, M.; Andrews, E.; Bigi, A.; Martucci, G.; Romanens, G.; Vogt, F.; Vuilleumier, L. Effects of the prewhitening method, the time granularity, and the time segmentation on the Mann–Kendall trend detection and the associated Sen’s slope. Atmos. Meas. Tech. 2020, 13, 6945–6964. [Google Scholar]
- Dawood, M. Spatio-statistical analysis of temperature fluctuation using Mann–Kendall and Sen’s slope approach. Clim. Dyn. 2017, 48, 783–797. [Google Scholar]
- Da Silva, R.M.; Santos, C.A.; Moreira, M.; Corte-Real, J.; Silva, V.C.; Medeiros, I.C. Rainfall and river flow trends using Mann–Kendall and Sen’s slope estimator statistical tests in the Cobres River basin. Nat. Hazards 2015, 77, 1205–1221. [Google Scholar]
- Kumar, N.; Panchal, C.; Chandrawanshi, S.; Thanki, J. Analysis of rainfall by using Mann-Kendall trend, Sen’s slope and variability at five districts of south Gujarat, India. Mausam 2017, 68, 205–222. [Google Scholar]
- Zheng, S.; Zhang, B.; Peng, D.; Yu, L.; Lin, B.; Pan, Y.; Xie, Q. The trend towards a warmer and wetter climate observed in arid and semi-arid areas of northwest China from 1959 to 2019. Environ. Res. Commun. 2021, 3, 115011. [Google Scholar]
- Tramblay, Y.; Koutroulis, A.; Samaniego, L.; Vicente-Serrano, S.M.; Volaire, F.; Boone, A.; Le Page, M.; Llasat, M.C.; Albergel, C.; Burak, S.; et al. Challenges for drought assessment in the Mediterranean region under future climate scenarios. Earth-Science Reviews. Earth-Sci. Rev. 2020, 210, 103348. [Google Scholar]
- Li, B.; Chen, Y.; Chen, Z.; Xiong, H.; Lian, L. Why does precipitation in northwest China show a significant increasing trend from 1960 to 2010? Atmos. Res. 2016, 167, 275–284. [Google Scholar]
- Liu, Y.; Liu, B.; Yang, X.; Bai, W.; Wang, J. Relationships between drought disasters and crop production during ENSO episodes across the North China Plain. Reg. Environ. Change 2015, 15, 1689–1701. [Google Scholar]
- Liu, Z.; Menzel, L.; Dong, C.; Fang, R. Temporal dynamics and spatial patterns of drought and the relation to ENSO: A case study in Northwest China. Int. J. Climatol. 2016, 36, 2886–2898. [Google Scholar]
- Zhang, W.; Jin, F.F.; Turner, A. Increasing autumn drought over southern China associated with ENSO regime shift. Geophys. Res. Lett. 2014, 41, 4020–4026. [Google Scholar]
- Gong, X.; Du, S.; Li, F.; Ding, Y. Study on the Spatial and Temporal Characteristics of Mesoscale Drought in China under Future Climate Change Scenarios. Water 2021, 13, 2761. [Google Scholar]
- Collados-Lara, A.J.; Pulido-Velazquez, D.; Pardo-Igúzquiza, E. A statistical tool to generate potential future climate scenarios for hydrology applications. Sci. Program. 2020, 2020, 1–11. [Google Scholar] [CrossRef]
- Pedro-Monzonís, M.; Solera, A.; Ferrer, J.; Estrela, T.; Paredes-Arquiola, J. A review of water scarcity and drought indexes in water resources planning and management. J. Hydrol. 2015, 527, 482–493. [Google Scholar] [CrossRef] [Green Version]






| Class | SPI | VCI | TCI | VHI | NVSWI | SMCI | SMADI |
|---|---|---|---|---|---|---|---|
| Moist | >1 | >50 | >50 | >50 | >80 | <10 | 0 to 0.49 |
| Abnormal | 1 to 0 | 40 to 50 | 40 to 50 | 40 to 50 | 60 to 80 | 10 to 20 | 0.5 to 1 |
| Mild | 0 to −0.99 | 30 to 40 | 30 to 40 | 30 to 40 | 40 to 60 | 20 to 30 | 1 to 1.99 |
| Moderate | −1 to −1.49 | 20 to 30 | 20 to 30 | 20 to 30 | 20 to 40 | 30 to 40 | 2 to 2.99 |
| Severe | −1.5 to −2 | 10 to 20 | 10 to 20 | 10 to 20 | 10 to 20 | 40 to 50 | 3 to 4 |
| Extreme | <−2 | 0 to 10 | 0 to 10 | 0 to 10 | <10 | >50 | >4 |
| Class | SPI-1 | SPI-3 | SPI-12 | VCI | TCI | VHI | NVSWI | SMCI | SMADI |
|---|---|---|---|---|---|---|---|---|---|
| SW | 48.09% | 68.07% | 91.19% | 93.45% | 21.21% | 88.34% | 75.64% | 68.75% | 85.17% |
| NSW | 35.37% | 22.84% | 5.81% | 4.87% | 49.00% | 6.74% | 14.95% | 13.40% | 12.08% |
| SD | 4.10% | 1.16% | 0.91% | 0.87% | 11.63% | 2.28% | 2.61% | 2.02% | 0.57% |
| NSD | 12.43% | 7.92% | 2.10% | 0.80% | 18.16% | 2.64% | 6.80% | 15.83% | 2.17% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, X.; Xia, H.; Liu, B.; Jiao, W. Spatiotemporal Comparison of Drought in Shaanxi–Gansu–Ningxia from 2003 to 2020 Using Various Drought Indices in Google Earth Engine. Remote Sens. 2022, 14, 1570. https://doi.org/10.3390/rs14071570
Zhao X, Xia H, Liu B, Jiao W. Spatiotemporal Comparison of Drought in Shaanxi–Gansu–Ningxia from 2003 to 2020 Using Various Drought Indices in Google Earth Engine. Remote Sensing. 2022; 14(7):1570. https://doi.org/10.3390/rs14071570
Chicago/Turabian StyleZhao, Xiaoyang, Haoming Xia, Baoying Liu, and Wenzhe Jiao. 2022. "Spatiotemporal Comparison of Drought in Shaanxi–Gansu–Ningxia from 2003 to 2020 Using Various Drought Indices in Google Earth Engine" Remote Sensing 14, no. 7: 1570. https://doi.org/10.3390/rs14071570