A Neural Network-Based Spectral Approach for the Assignment of Individual Trees to Genetically Differentiated Subpopulations
Abstract
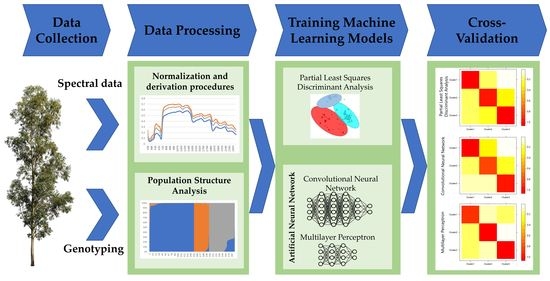
:1. Introduction
2. Materials and Methods
2.1. Study Population
2.2. High-Throughput Phenotyping
2.3. High-Throughput Genotyping and Population Genetic Structure
2.4. Classification Analysis
2.4.1. Partial Least Squares Discriminant Analysis (PLS-DA)
2.4.2. Convolutional Neural Network (CNN)
- (I)
- Input layer: used to load the input data.
- (II)
- Conv1D layer: In this layer, the high-level features from the spectral data are extracted through a kernel matrix (or weight matrix). For this, the weights rotate over the spectral matrix in a sliding window from which the convolved output is obtained and the weights are learned in order to minimize the loss function. This layer utilizes the following parameters:Kernels: The convolution output c[n] is given as:where x[n] and k[n] denote the input vector and convolution kernel, respectively, while ∗ denotes the convolution operation between both. In general, the convolved feature in the output of lth layer can be written as:where and denote the ith and jth features of the lth and (l − 1)th layers, respectively; represents the kernel linked from the ith to jth features; represents the bias for the corresponding feature; and represents the activation function used (ReLU, Sigmoid, or Tanh), which is in charge of capturing the nonlinearity of the input signal.Filters: The He uniform variance scaling initializer was used to initialize the filter weights, while the bias vector was set to zero.
- (III)
- Dense layer: The dense layer represents a deeply connected neural network layer (fully connected layer) with its preceding layer, which means the neurons between this layer and its preceding layer are fully connected. In general, the dense layer operation can be represented as:where represents a dot product between the weight vector of this layer and the , denotes the bias vector for this layer, and is the activation function (ReLU, Sigmoid, or Tanh) used.
- (IV)
- 1D max pooling layer (Maxpool1D): This layer reduces the resolution by dividing the input into 1D pooling regions and then computing the maximum value of the feature map in each region. The operation of max pooling is given as:where represents the pooling region with index .
- (V)
- Flatten layer and dropout: This layer is used to flatten the input, creating a one-dimensional vector through the input data. The dropout parameter helps reduce overfitting in the training process.
- (VI)
- Output layer (dense layer for classification): This layer employs the softmax activation function for multi-class classification problem. The softmax activation function is given by:where z is an input vector, which represents the elements of the output vector of the previous layer, M is the number of categories, and pi denotes the output domain of categorical probabilities.
2.4.3. Multilayer Perceptron (MLP)
2.4.4. Performance Metric
3. Results
3.1. Hyperparameter Optimization in the MLP and CNN Models
3.2. Spectral-Based Classification
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| Abbreviation | Definition |
| Adam | Stochastic gradient descent method that is based on adaptive estimation of first-order and second-order moments |
| CNN | Convolutional Neural Network |
| Conv1D | 1D Convolutional Neural Network |
| Dense layers | Regular deeply connected neural network layer |
| MaxPooling1D | Maximum one-dimensional sampling |
| MLP | Multilayer Perceptron |
| PLS-DA | Partial Least Squares Discriminant Analysis |
| ReLU | Rectified linear unit activation function |
| rmsprop | Root Mean Square Propagation |
| SNP | Single-Nucleotide Polymorphisms |
| softmax | Normalized exponential function activation function |
| Tanh | Hyperbolic tangent activation function |
References
- Stift, M.; Kolář, F.; Meirmans, P.G. Structure is more robust than other clustering methods in simulated mixed-ploidy populations. Heredity 2019, 123, 429–441. [Google Scholar] [CrossRef] [PubMed]
- Perez, S.D.; Grummer, J.A.; Fernandes-Santos, R.C.; Jose, C.T.; Medici, E.P.; Marcili, A. Phylogenetics, patterns of genetic variation and population dynamics of Trypanosoma terrestris support both coevolution and ecological host-fitting as processes driving trypanosome evolution. Parasit. Vectors 2019, 12, 473. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Feng, H.; Guo, Z.; Yang, W.; Huang, C.; Chen, G.; Fang, W.; Xiong, X.; Zhang, H.; Wang, G.; Xiong, L.; et al. An integrated hyperspectral imaging and genome-wide association analysis platform provides spectral and genetic insights into the natural variation in rice. Sci. Rep. 2017, 7, 4401. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lopez-Cortes, X.A.; Matamala, F.; Maldonado, C.; Mora-Poblete, F.; Scapim, C.A. A Deep Learning Approach to Population Structure Inference in Inbred Lines of Maize. Front. Genet. 2020, 11, 543459. [Google Scholar] [CrossRef] [PubMed]
- Alhusain, L.; Hafez, A.M. Nonparametric approaches for population structure analysis. Hum. Genet. 2018, 12, 25. [Google Scholar] [CrossRef] [Green Version]
- Aalbers, S.E.; Hipp, M.J.; Kennedy, S.R.; Weir, B.S. Analyzing population structure for forensic STR markers in next generation sequencing data. Forensic Sci. Int. Genet. 2020, 49, 102364. [Google Scholar] [CrossRef]
- Luo, Z.; Brock, J.; Dyer, J.M.; Kutchan, T.; Schachtman, D.; Augustin, M.; Ge, Y.; Fahlgren, N.; Abdel-Haleem, H. Genetic diversity and population structure of a Camelina sativa spring panel. Front. Plant Sci. 2019, 10, 184. [Google Scholar] [CrossRef] [Green Version]
- Porras-Hurtado, L.; Ruiz, Y.; Santos, C.; Phillips, C.; Carracedo, Á.; Lareu, M. An overview of STRUCTURE: Applications, parameter settings, and supporting software. Front. Genet. 2013, 4, 98. [Google Scholar] [CrossRef] [Green Version]
- Wambugu, P.W.; Ndjiondjop, M.N.; Henry, R.J. Role of genomics in promoting the utilization of plant genetic resources in genebanks. Brief. Funct. Genom. 2018, 17, 198–206. [Google Scholar] [CrossRef]
- Khadka, K.; Torkamaneh, D.; Kaviani, M.; Belzile, F.; Raizada, M.N.; Navabi, A. Population structure of Nepali spring wheat (Triticum aestivum L.) germplasm. BMC Plant Biol. 2020, 20, 530. [Google Scholar] [CrossRef]
- Tehseen, M.M.; Istipliler, D.; Kehel, Z.; Sansaloni, C.P.; da Silva Lopes, M.; Kurtulus, E.; Muazzam, S.; Nazari, K. Genetic diversity and population structure analysis of Triticum aestivum L. landrace panel from Afghanistan. Genes 2021, 12, 340. [Google Scholar] [CrossRef] [PubMed]
- Gordon, E.; Kaviani, M.; Kagale, S.; Payne, T.; Navabi, A. Genetic diversity and population structure of synthetic hexaploid-derived wheat (Triticum aestivum L.) accessions. Genet. Resour. Crop. Evol. 2018, 66, 335–348. [Google Scholar] [CrossRef]
- Ballesta, P.; Mora, F.; Del Pozo, A. Association mapping of drought tolerance indices in wheat: QTL-rich regions on chromosome 4A. Sci. Agric. 2020, 77, e20180153. [Google Scholar] [CrossRef] [Green Version]
- Emanuelli, F.; Lorenzi, S.; Grzeskowiak, L.; Catalano, V.; Stefanini, M.; Troggio, M.; Myles, S.; Martinez-Zapater, J.M.; Zyprian, E.; Moreira, F.M.; et al. Genetic diversity and population structure assessed by SSR and SNP markers in a large germplasm collection of grape. BMC Plant Biol. 2013, 13, 39. [Google Scholar] [CrossRef] [Green Version]
- Sant'Ana, G.C.; Espolador, F.G.; Granato, Í.S.C.; Mendonça, L.F.; Fritsche-Neto, R.; Borém, A. Population structure analysis and identification of genomic regions under selection associated with low-nitrogen tolerance in tropical maize lines. PLoS ONE 2020, 15, e0239900. [Google Scholar] [CrossRef] [PubMed]
- Tsykun, T.; Rellstab, C.; Dutech, C.; Sipos, G.; Prospero, S. Comparative assessment of SSR and SNP markers for inferring the population genetic structure of the common fungus Armillaria cepistipes. Heredity 2017, 119, 371–380. [Google Scholar] [CrossRef]
- Badu-Apraku, B.; Garcia-Oliveira, A.L.; Petroli, C.D.; Hearne, S.; Adewale, S.A.; Gedil, M. Genetic diversity and population structure of early and extra-early maturing maize germplasm adapted to sub-Saharan Africa. BMC Plant Biol. 2021, 21, 96. [Google Scholar] [CrossRef]
- Yang, X.; Tan, B.; Liu, H.; Zhu, W.; Xu, L.; Wang, Y.; Kang, H. Genetic Diversity and Population Structure of Asian and European Common Wheat Accessions Based on Genotyping-By-Sequencing. Front. Genet. 2020, 11, 1157. [Google Scholar] [CrossRef]
- Soumya, P.R.; Burridge, A.J.; Singh, N.; Batra, R.; Pandey, R.; Kalia, S.; Rai, V.; Edwards Edwards, K.J. Population structure and genome-wide association studies in bread wheat for phosphorus efficiency traits using 35 K Wheat Breeder’s Affymetrix array. Sci. Rep. 2021, 11, 7601. [Google Scholar] [CrossRef]
- Tekeu, H.; Ngonkeu, E.L.; Bélanger, S.; Djocgoué, P.F.; Abed, A.; Torkamaneh, D.; Boyle, B.; Tsimi, P.M.; Tadesse, W.; Jean, M.; et al. GWAS identifies an ortholog of the rice D11 gene as a candidate gene for grain size in an international collection of hexaploid wheat. Sci. Rep. UK 2021, 11, 19483. [Google Scholar] [CrossRef]
- Vejchasarn, P.; Shearman, J.R.; Chaiprom, U.; Phansenee, Y.; Suthanthangjai, A.; Jairin, J.; Chamarerk, V.; Tulyananda, T.; Amornbunchornvej, C. Population structure of nation-wide rice in Thailand. Rice 2021, 14, 88. [Google Scholar] [CrossRef] [PubMed]
- Aesomnuk, W.; Ruengphayak, S.; Ruanjaichon, V.; Sreewongchai, T.; Malumpong, C.; Vanavichit, A.; Toojinda, T.; Wanchana, S.; Arikit, S. Estimation of the genetic diversity and population structure of Thailand’s rice landraces using SNP markers. Agronomy 2021, 11, 995. [Google Scholar] [CrossRef]
- Pailles, Y.; Ho, S.; Pires, I.S.; Tester, M.; Negrão, S.; Schmöcke, S.M. Genetic diversity and population structure of two tomato species from the galapagos islands. Front. Plant Sci. 2017, 8, 138. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wang, X.; Gao, L.; Jiao, C.; Stravoravdis, S.; Hosmani, P.S.; Saha, S.; Zhang, J.; Mainiero, S.; Strickler, S.R.; Catala, C.; et al. Genome of Solanum pimpinellifolium provides insights into structural variants during tomato breeding. Nat. Commun. 2020, 11, 5817. [Google Scholar] [CrossRef] [PubMed]
- Mora-Poblete, F.; Ballesta, P.; Lobos, G.A.; Molina-Montenegro, M.; Gleadow, R.; Ahmar, S.; Jimenez-Aspee, F. Genome-wide association study of cyanogenic glycosides, proline, sugars, and pigments in Eucalyptus cladocalyx after 18 consecutive dry summers. Physiol. Plant. 2021, 172, 1550–1569. [Google Scholar] [CrossRef]
- Valenzuela, C.E.; Ballesta, P.; Ahmar, S.; Fiaz, S.; Heidari, P.; Maldonado, C.; Mora-Poblete, F. Haplotype-and SNP-Based GWAS for Growth and Wood Quality Traits in Eucalyptus cladocalyx Trees under Arid Conditions. Plants 2021, 10, 148. [Google Scholar] [CrossRef]
- Yang, H.; Xu, F.; Liao, H.; Zhang, W.; Yang, X.; Xu, B.; Pan, W. Correction to: Genome-wide assessment of population structure and genetic diversity of Eucalyptus urophylla based on a multi-species single-nucleotide polymorphism chip analysis. Tree Genet. Genomes 2020, 16, 39. [Google Scholar] [CrossRef]
- Kitada, S.; Nakamichi, R.; Kishino, H. Understanding population structure in an evolutionary context: Population-specific FST and pairwise FST. G3 2021, 11, jkab316. [Google Scholar] [CrossRef]
- Keller, S.R.; Olson, M.S.; Silim, S.; Schroeder, W.; Tiffin, P. Genomic diversity, population structure, and migration following rapid range expansion in the Balsam poplar, Populus balsamifera. Mol. Ecol. 2010, 19, 1212–1226. [Google Scholar] [CrossRef]
- Chen, C.; Chu, Y.; Ding, C.; Su, X.; Huang, Q. Genetic diversity and population structure of black cottonwood (Populus deltoides) revealed using simple sequence repeat markers. BMC Genet. 2020, 21, 2. [Google Scholar] [CrossRef] [Green Version]
- Gogolev, Y.V.; Ahmar, S.; Akpinar, B.A.; Budak, H.; Kiryushkin, A.S.; Gorshkov, V.Y.; Hensel, G.; Demchenko, K.N.; Kovalchuk, I.; Mora-Poblete, F.; et al. Omics, epigenetics, and genome editing techniques for food and nutritional security. Plants 2021, 10, 1423. [Google Scholar] [CrossRef] [PubMed]
- Costa, C.; Schurr, U.; Loreto, F.; Menesatti, P.; Carpentier, S. Plant Phenotyping Research Trends, a Science Mapping Approach. Front. Plant Sci. 2019, 9, 1933. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Pérez-Valencia, D.M.; Rodríguez-Álvarez, M.X.; Boer, M.P.; Kronenberg, L.; Hund, A.; Cabrera-Bosquet, L.; Millet, E.J.; van Eeuwijk, F.A. A two-stage approach for the spatio-temporal analysis of high-throughput phenotyping data. Sci. Rep. 2021, 12, 3177. [Google Scholar] [CrossRef] [PubMed]
- Awad, M.M.; Alawar, B.; Jbeily, R. A new crop spectral signatures database interactive tool (CSSIT). Data 2019, 4, 77. [Google Scholar] [CrossRef] [Green Version]
- Huang, A.; Zhou, Q.; Liu, J.; Fei, B.; Sun, S. Distinction of three wood species by Fourier transform infrared spectroscopy and two-dimensional correlation IR spectroscopy. J. Mol. Struct. 2008, 883, 160–166. [Google Scholar] [CrossRef]
- Duca, D.; Mancini, M.; Rossini, G.; Mengarelli, C.; Pedretti, E.F.; Toscano, G.; Pizzi, A. Soft independent modelling of class analogy applied to infrared spectroscopy for rapid discrimination between hardwood and softwood. Energy 2016, 117, 251–258. [Google Scholar] [CrossRef]
- Liu, J.; Zhang, K.; Wu, S.; Shi, H.; Zhao, Y.; Sun, Y.; Zhuang, H.; Fu, E. An Investigation of a Multidimensional CNN Combined with an Attention Mechanism Model to Resolve Small-Sample Problems in Hyperspectral Image Classification. Remote Sens. 2022, 14, 78. [Google Scholar] [CrossRef]
- Hu, X.; Li, T.; Zhou, T.; Peng, Y. Deep Spatial-Spectral Subspace Clustering for Hyperspectral Images Based on Contrastive Learning. Remote Sens. 2022, 13, 4418. [Google Scholar] [CrossRef]
- Lin, M.; Jing, W.; Di, D.; Chen, G.; Song, H. Multi-Scale U-Shape MLP for Hyperspectral Image Classification. IEEE Geosci. Remote Sens. Lett. 2022, 19, 6006105. [Google Scholar] [CrossRef]
- Torada, L.; Lorenzon, L.; Beddis, A.; Isildak, U.; Pattini, L.; Mathieson, S.; Fumagalli, M. ImaGene: A convolutional neural network to quantify natural selection from genomic data. BMC Bioinform. 2019, 20, 337. [Google Scholar] [CrossRef]
- Arriagada, O.; Mora, F.; Amaral Junior, A.T. Thirteen years under arid conditions: Exploring marker-trait associations in Eucalyptus cladocalyx for complex traits related to flowering, stem form and growth. Breed. Sci. 2018, 68, 367–374. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ballesta, P.; Bush, D.; Silva, F.F.; Mora, F. Genomic predictions using low-density SNP markers, pedigree and GWAS information: A case study with the non-model species Eucalyptus cladocalyx. Plants 2020, 9, 99. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2018. [Google Scholar]
- Ballesta, P.; Ahmar, S.; Lobos, G.A.; Mieres-Castro, D.; Jiménez-Aspee, F.; Mora-Poblete, F. Heritable Variation of Foliar Spectral Reflectance Enhances Genomic Prediction of Hydrogen Cyanide in a Genetically Structured Population of Eucalyptus. Front. Plant Sci. 2022, 13, 769. [Google Scholar] [CrossRef] [PubMed]
- Porebski, S.; Bailey, L.G.; Baum, B.R. Modification of a CTAB DNA extraction protocol for plants containing high polysaccharide and polyphenol components. Plant Mol. Biol. Rep. 1997, 15, 8–15. [Google Scholar] [CrossRef]
- Doyle, J.J.; Doyle, J.L. Isolation of plant DNA from fresh tissue. Focus 1990, 12, 13–15. [Google Scholar]
- Bradbury, P.J.; Zhang, Z.; Kroon, D.E.; Casstevens, T.M.; Ramdoss, Y.; Buckler, E.S. TASSEL: Software for association mapping of complex traits in diverse samples. Bioinformatics 2007, 23, 2633–2635. [Google Scholar] [CrossRef]
- Evanno, G.; Regnaut, S.; Goudet, J. Detecting the number of clusters of individuals using the software STRUCTURE: A simulation study. Mol. Ecol. 2005, 14, 2611–2620. [Google Scholar] [CrossRef] [Green Version]
- Mora, F.; Castillo, D.; Lado, B.; Matus, I.; Poland, J.; Belzile, F.; Von Zitzewitz, J.; Del Pozo, A. Genome-wide association mapping of agronomic traits and carbon isotope discrimination in a worldwide germplasm collection of spring wheat using SNP markers. Mol. Breed. 2015, 35, 69. [Google Scholar] [CrossRef]
- Lottering, R.T.; Govender, M.; Peerbhay, K.; Lottering, S. Comparing Partial Least Squares (PLS) Discriminant Analysis and Sparse PLS Discriminant Analysis in Detecting and Mapping Solanum Mauritianum in Commercial Forest Plantations Using Image Texture. ISPRS J. Photogramm. Remote Sens. 2020, 159, 271–280. [Google Scholar] [CrossRef]
- Sanchez, G. Package ‘DiscriMiner’. 2013. Available online: https://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.408.5145&rep=rep1&type=pdf (accessed on 3 January 2022).
- Nezami, S.; Khoramshahi, E.; Nevalainen, O.; Pölönen, I.; Honkavaara, E. Tree species classification of drone hyperspectral and rgb imagery with deep learning convolutional neural networks. Remote Sens. 2020, 12, 1070. [Google Scholar] [CrossRef] [Green Version]
- Kawamura, K.; Nishigaki, T.; Andriamananjara, A.; Rakotonindrina, H.; Tsujimoto, Y.; Moritsuka, N.; Rabenarivo, M.; Razafimbelo, T. Using a One-Dimensional Convolutional Neural Network on Visible and Near-Infrared Spectroscopy to Improve Soil Phosphorus Prediction in Madagascar. Remote Sens. 2021, 13, 1519. [Google Scholar] [CrossRef]
- Zhang, L.; Ding, X.; Hou, R. Classification modeling method for near-infrared spectroscopy of tobacco based on multimodal convolution neural networks. J. Anal. Methods Chem. 2020, 22, 1–13. [Google Scholar] [CrossRef] [PubMed]
- Peng, D.; Liu, Z. A Novel Deeper One-Dimensional CNN with Residual Learning for Fault Diagnosis of Wheelset Bearings in High-Speed Trains. IEEE Access 2018, 99, 10278–10293. [Google Scholar] [CrossRef]
- Botalb, A.; Moinuddin, M.; Al-Saggaf, U.M.; Ali, S.S.A. Contrasting convolutional neural network (CNN) with multi-layer perceptron (MLP) for big data analysis. In Proceedings of the 2018 International Conference on Intelligent and Advanced System, Kuala Lumpur, Malaysia, 13–14 August 2018. [Google Scholar]
- Taravat, A.; Proud, S.; Peronaci, S.; Del Frate, F.; Oppelt, N. Multilayer Perceptron Neural Networks Model for Meteosat Second Generation SEVIRI Daytime Cloud Masking. Remote Sens. 2015, 7, 1529–1539. [Google Scholar] [CrossRef] [Green Version]
- Hauser, L.T.; Timmermans, J.; van der Windt, N.; Sil, Â.F.; César de Sá, N.; Soudzilovskaia, N.A.; van Bodegom, P.M. Explaining discrepancies between spectral and in-situ plant diversity in multispectral satellite earth observation. Remote Sens. Environ. 2021, 265, 112684. [Google Scholar] [CrossRef]
- Zeng, F.; Peng, W.; Kang, G.; Feng, Z.; Yue, X. Spectral Data Classification by One-Dimensional Convolutional Neural Networks. In Proceedings of the 2021 IEEE International Performance, Computing, and Communications Conference (IPCCC), Austin, TX, USA, 29–31 October 2021; pp. 1–6. [Google Scholar]
- Britz, R.; Barta, N.; Schaumberger, A.; Klingler, A.; Bauer, A.; Pötsch, E.M.; Gronauer, A.; Motsch, V. Spectral-Based Classification of Plant Species Groups and Functional Plant Parts in Managed Permanent Grassland. Remote Sens. 2022, 14, 1154. [Google Scholar] [CrossRef]
- Pritchard, J.K.; Stephens, M.; Donnelly, P. Inference of population structure using multilocus genotype data. Genetics 2000, 155, 945–959. [Google Scholar] [CrossRef]
- Tonkin-Hill, G.; Lees, J.A.; Bentley, S.D.; Frost, S.D.; Corander, J. Fast hierarchical Bayesian analysis of population structure. Nucleic Acids Res. 2019, 47, 5539–5549. [Google Scholar] [CrossRef] [Green Version]
- Raj, A.; Stephens, M.; Pritchard, J.K. fastSTRUCTURE: Variational inference of population structure in large SNP data sets. Genetics 2014, 197, 573–589. [Google Scholar] [CrossRef] [Green Version]
- Alexander, D.H.; Novembre, J.; Lange, K. Fast model-based estimation of ancestry in unrelated individuals. Genome Res. 2009, 19, 1655–1664. [Google Scholar] [CrossRef] [Green Version]
- Ferreira, F.; Scapim, C.A.; Maldonado, C.; Mora, F. SSR-based genetic analysis of sweet corn inbred lines using artificial neural networks. Crop Breed. Appl. Biotechnol. 2018, 18, 309–313. [Google Scholar] [CrossRef]
- Kulka, V.P.; Silva, T.A.D.; Contreras-Soto, R.I.; Maldonado, C.; Mora, F.; Scapim, C.A. Diallel analysis and genetic differentiation of tropical and temperate maize inbred lines. Crop Breed. Appl. Biotechnol. 2018, 18, 31–38. [Google Scholar] [CrossRef] [Green Version]
- Costa, M.O.; Capel, L.S.; Maldonado, C.; Mora, F.; Mangolin, C.A.; Machado, M.D. High genetic differentiation of grapevine rootstock varieties determined by molecular markers and artificial neural networks. Acta Sci. Agron. 2019, 42, e43475. [Google Scholar] [CrossRef] [Green Version]
- Jombart, T. adegent: A R package for the multivariate analysis of genetic markers. Bioinformatics 2008, 24, 1403–1405. [Google Scholar] [CrossRef] [Green Version]
- Jetz, W.; Cavender-Bares, J.; Pavlick, R.; Schimel, D.; Davis, F.W.; Asner, G.P.; Guralnick, R.; Kattge, J.; Latimer, A.M.; Moorcroft, P.; et al. Monitoring plant functional diversity from space. Nat. Plants 2016, 2, 16024. [Google Scholar] [CrossRef] [Green Version]
- Wang, R.; Gamon, J.A. Remote sensing of terrestrial plant biodiversity. Remote Sens. Environ. 2019, 231, 111218. [Google Scholar] [CrossRef]
- Schwager, P.; Berg, C. Remote sensing variables improve species distribution models for alpine plant species. Basic Appl. Ecol. 2021, 54, 1–13. [Google Scholar] [CrossRef]
- Monteiro, A.T.; Alves, P.; Carvalho-Santos, C.; Lucas, R.; Cunha, M.; Marques da Costa, E.; Fava, F. Monitoring Plant Diversity to Support Agri-Environmental Schemes: Evaluating Statistical Models Informed by Satellite and Local Factors in Southern European Mountain Pastoral Systems. Diversity 2021, 14, 8. [Google Scholar] [CrossRef]
- Zhang, J.; He, Y.; Yuan, L.; Liu, P.; Zhou, X.; Huang, Y. Machine Learning-Based Spectral Library for Crop Classification and Status Monitoring. Agronomy 2019, 9, 496. [Google Scholar] [CrossRef] [Green Version]
- Yu, Z.; Fang, H.; Zhangjin, Q.; Mi, C.; Feng, X.; He, Y. Hyperspectral imaging technology combined with deep learning for hybrid okra seed identification. Biosyst. Eng. 2021, 212, 46–61. [Google Scholar] [CrossRef]
- Qiu, Z.J.; Chen, J.; Zhao, Y.Y.; Zhu, S.S.; He, Y.; Zhang, C. Variety Identification of Single Rice Seed Using Hyperspectral Imaging Combined with Convolutional Neural Network. Appl. Sci. 2018, 8, 212. [Google Scholar] [CrossRef] [Green Version]
- Naeem, S.; Ali, A.; Chesneau, C.; Tahir, M.H.; Jamal, F.; Sherwani, R.A.K.; Ul Hassan, M. The Classification of Medicinal Plant Leaves Based on Multispectral and Texture Feature Using Machine Learning Approach. Agronomy 2021, 11, 263. [Google Scholar] [CrossRef]
- Yu, H.; Samuels, D.C.; Zhao, Y.Y.; Guo, Y. Architectures and accuracy of artificial neural network for disease classification from omics data. BMC Genom. 2019, 20, 167. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Fernandez, A.; Garcìa, S.; Galar, M.; Prati, R.C.; Krawczyk, B.; Herrera, F. Learning from Imbalanced Data Sets; Springer: New York, NY, USA, 2018; ISBN 978-3-319-98073-7. [Google Scholar]
- Rincent, R.; Charpentier, J.; Faivre-Rampant, P.; Paux, E.; Le Gouis, J.; Bastien, C.; Segura, V. Phenomic Selection Is a Low-Cost and High-Throughput Method Based on Indirect Predictions: Proof of Concept on Wheat and Poplar. G3 Genes Genomes Genet. 2018, 8, 3961–3972. [Google Scholar] [CrossRef] [Green Version]


| Parameter | Values Used |
|---|---|
| Activation functions | ReLU, Tanh and Sigmoid |
| Dense layers | MLP: 1 or 2; CNN: 1 or 2 extra |
| Optimizer algorithm | Adam and rmsprop |
| Batch size | 10, 20 and 40 |
| Activation Function | Layers (N°) | Optimizer | Batch Size | MLP | CNN |
|---|---|---|---|---|---|
| ReLu | 1 | Adam | 10 | 0.87 * | 0.85 * |
| 20 | 0.82 | 0.82 | |||
| 40 | 0.84 | 0.77 | |||
| rmsprop | 10 | 0.66 | 0.76 | ||
| 20 | 0.73 | 0.78 | |||
| 40 | 0.67 | 0.72 | |||
| 2 | Adam | 10 | 0.80 | 0.69 | |
| 20 | 0.84 | 0.8 | |||
| 40 | 0.79 | 0.78 | |||
| rmsprop | 10 | 0.66 | 0.78 | ||
| 20 | 0.70 | 0.79 | |||
| 40 | 0.63 | 0.8 | |||
| Sigmoid | 1 | Adam | 10 | 0.84 | 0.78 |
| 20 | 0.73 | 0.63 | |||
| 40 | 0.79 | 0.51 | |||
| rmsprop | 10 | 0.80 | 0.76 | ||
| 20 | 0.77 | 0.72 | |||
| 40 | 0.64 | 0.63 | |||
| 2 | Adam | 10 | 0.62 | 0.49 | |
| 20 | 0.63 | 0.52 | |||
| 40 | 0.73 | 0.54 | |||
| rmsprop | 10 | 0.64 | 0.5 | ||
| 20 | 0.85 | 0.51 | |||
| 40 | 0.79 | 0.49 | |||
| Tanh | 1 | Adam | 10 | 0.69 | 0.77 |
| 20 | 0.77 | 0.76 | |||
| 40 | 0.68 | 0.74 | |||
| rmsprop | 10 | 0.79 | 0.74 | ||
| 20 | 0.65 | 0.66 | |||
| 40 | 0.63 | 0.78 | |||
| 2 | Adam | 10 | 0.82 | 0.8 | |
| 20 | 0.75 | 0.75 | |||
| 40 | 0.68 | 0.74 | |||
| rmsprop | 10 | 0.79 | 0.7 | ||
| 20 | 0.81 | 0.69 | |||
| 40 | 0.81 | 0.67 |
| Classification Accuracy * | ||||
|---|---|---|---|---|
| Model | Overall | Class 1 | Class 2 | Class 3 |
| Multilayer Perceptron | 0.87 (0.03) | 0.84 (0.05) | 0.92 (0.08) | 0.91 (0.08) |
| Convolutional Neural Network | 0.86 (0.03) | 0.87 (0.07) | 0.76 (0.14) | 0.88 (0.10) |
| Partial Least-Squares Discriminant Analysis | 0.81 (0.03) | 0.82 (0.05) | 0.78 (0.14) | 0.82 (0.09) |
| Individuals in class | 296 | 155 | 52 | 89 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Maldonado, C.; Mora-Poblete, F.; Echeverria, C.; Baettig, R.; Torres-Díaz, C.; Contreras-Soto, R.I.; Heidari, P.; Lobos, G.A.; do Amaral Júnior, A.T. A Neural Network-Based Spectral Approach for the Assignment of Individual Trees to Genetically Differentiated Subpopulations. Remote Sens. 2022, 14, 2898. https://doi.org/10.3390/rs14122898
Maldonado C, Mora-Poblete F, Echeverria C, Baettig R, Torres-Díaz C, Contreras-Soto RI, Heidari P, Lobos GA, do Amaral Júnior AT. A Neural Network-Based Spectral Approach for the Assignment of Individual Trees to Genetically Differentiated Subpopulations. Remote Sensing. 2022; 14(12):2898. https://doi.org/10.3390/rs14122898
Chicago/Turabian StyleMaldonado, Carlos, Freddy Mora-Poblete, Cristian Echeverria, Ricardo Baettig, Cristian Torres-Díaz, Rodrigo Iván Contreras-Soto, Parviz Heidari, Gustavo Adolfo Lobos, and Antônio Teixeira do Amaral Júnior. 2022. "A Neural Network-Based Spectral Approach for the Assignment of Individual Trees to Genetically Differentiated Subpopulations" Remote Sensing 14, no. 12: 2898. https://doi.org/10.3390/rs14122898