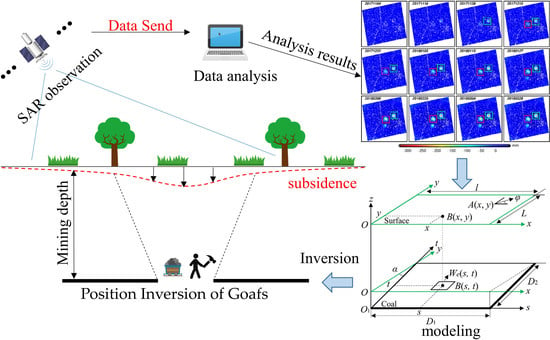
Position Inversion of Goafs in Deep Coal Seams Based on DS-InSAR Data and the Probability Integral Methods
Abstract
:1. Introduction
2. Materials and Methods
2.1. DS-InSAR Method
2.2. Probability Integral Model
2.3. Establishment of Inversion Model
3. Results
3.1. Simulations
Numerical Simulations
3.2. Experiments with Real Data
3.2.1. Study Area
3.2.2. SAR Data Processing
3.2.3. Inversion of Goaf Parameters
4. Discussion
4.1. Goaf Inversion with Known PIM Parameters
4.2. Influence of the LOS Deformation Obtained by DS-InSAR
5. Conclusions
- (1)
- The amount of surface deformation data used is very important to constrain the inversion model. Therefore, DS-InSAR is applied to reduce the influence of spatio-temporal incoherence, and this can effectively increase the density and accuracy of the field-observed deformations.
- (2)
- For mining subsidence caused by exploitation of deep coal seams, the center of the surface deformation deviates from the position of the underground goaf due to the coal seam dip angle. Thus, the center deviation caused by inclined coal seams in the model must be considered, or the inversion error in the center coordinate will be larger.
- (3)
- Simulation results show that it is feasible to use the PIM parameters as unknown parameters in goaf inversion, and the inversion errors are relatively small. Experiments with real data verified the results of the simulations. In the case of the PIM parameters being involved in the inversion, the goaf position parameters can still be obtained with a high accuracy. Because the PIM parameters are difficult to obtain accurately, the method in this paper avoids the need for their selection according to experience in goaf location inversion.
- (4)
- The maximum relative error of the simulations was 2.11%, the maximum relative error in the experiments with real data was 26.67%, and the errors in other inversion parameters were relatively small. The experimental results show that the method has a good effect on the inversion of underground goaf locations and has the advantage of a large range of non-contact measurements.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wu, W.D.; Bai, J.B.; Yan, S.; Wang, X.Y.; Wu, B.W. Planning and design of underground space construction during longwall mining in coal mines. Energy Sources 2020. [Google Scholar] [CrossRef]
- Liu, H.; Zhang, M.; Su, L.J.; Chen, X.X.; Liu, C.F.; Sun, A.G. A boundary model of terrain reconstruction in a coal-mining subsidence waterlogged area. Environ. Earth Sci. 2021, 80, 187. [Google Scholar] [CrossRef]
- Blanchette, M.L.; Mark, A.L. Pit lakes are a global legacy of mining: An integrated approach to achieving sustainable ecosystems and value for communities. Curr. Opin. Environ. Sustain. 2016, 23, 28–34. [Google Scholar] [CrossRef]
- Cui, X.M.; Gao, Y.G.; Yuan, D.B. Sudden surface collapse disasters caused by shallow partial mining in Datong coalfield, China. Nat. Hazards 2014, 74, 911–929. [Google Scholar] [CrossRef]
- Guo, Q.B.; Guo, G.L.; Li, Y.M.; Wang, L.; Zhao, X.W. Stability evaluation of an expressway construction site above an abandoned coal mine based on the overlay and index method. Sustainability 2019, 11, 5163. [Google Scholar] [CrossRef] [Green Version]
- Bell, F.G.; Stacey, T.R.; Genske, D.D. Mining subsidence and its effect on the environment: Some differing examples. Environ. Geol. 2000, 40, 135–152. [Google Scholar] [CrossRef]
- Liu, B.C.; Dai, H.Y. Research development and origin of probability integral method. Coal Min. Technol. 2016, 21, 1–3. [Google Scholar]
- Wang, L.; Wei, T.; Li, N.; Chi, S.S.; Jiang, C.; Fang, S.Y. Research on probability integration parameter inversion of mining-induced surface subsidence based on quantum annealing. Environ. Earth Sci. 2018, 77, 740. [Google Scholar] [CrossRef]
- Yang, Z.F.; Li, Z.W.; Zhu, J.J.; Yi, H.W.; Feng, G.C.; Hu, J.; Wu, L.X.; Preusse, A.; Wang, Y.J.; Papst, M. Locating and defining underground goaf caused by coal mining from space-borne SAR interferometry. ISPRS J. Photogramm. Remote Sens. 2018, 135, 112–126. [Google Scholar] [CrossRef]
- Shi, Y.; Li, Q.W.; Meng, X.; Zhang, T.K.; Shi, J.J. On time-series InSAR by SA-SVR algorithm: Prediction and analysis of mining subsidence. J. Sens. 2020, 2020, 8860225. [Google Scholar] [CrossRef]
- Fan, H.D.; Wang, L.; Wen, B.F.; Du, S. A new model for three-dimensional deformation extraction with single-track InSAR based on mining subsidence characteristics. Int. J. Appl. Earth Obs. Geoinf. 2021, 94, 102223. [Google Scholar] [CrossRef]
- Kamali, M.E.; Abuelgasim, A.; Papoutsis, I.; Loupasakis, C.; Kontoes, C. A reasoned bibliography on SAR interferometry applications and outlook on big interferometric data processing. Remote Sens. Appl. Soc. Environ. 2020, 19, 100358. [Google Scholar]
- Du, W.B.; Ji, W.Q.; Xu, L.J.; Wang, S.T. Deformation time series and driving-force analysis of glaciers in the eastern Tienshan mountains using the SBAS InSAR method. Int. J. Environ. Res. Public Health 2020, 17, 2836. [Google Scholar] [CrossRef] [Green Version]
- Baffelli, S.; Frey, O.; Hajnsek, I. Geostatistical analysis and mitigation of the atmospheric phase screens in Ku-band terrestrial radar interferometric observations of an Alpine glacier. IEEE Trans. Geosci. Remote Sens. 2020, 58, 7533–7556. [Google Scholar] [CrossRef]
- Delgado, F. Rhyolitic volcano dynamics in the Southern Andes: Contributions from 17 years of InSAR observations at Cordón Caulle volcano from 2003 to 2020. J. South Am. Earth Sci. 2021, 106, 102841. [Google Scholar] [CrossRef]
- Gaddes, M.E.; Hooper, A.; Bagnardi, M.; Inman, H.; Albino, F. Blind signal separation methods for InSAR: The potential to automatically detect and monitor signals of volcanic deformation. J. Geophys. Res. Solid Earth 2018, 123, 10226–10251. [Google Scholar] [CrossRef] [Green Version]
- Pepe, A.; Calò, F. A review of interferometric synthetic aperture radar (InSAR) multi-track approaches for the retrieval of earth’s surface displacements. Appl. Sci. 2017, 7, 1264. [Google Scholar] [CrossRef] [Green Version]
- Xu, G.Y.; Xu, C.J.; Wen, Y.M.; Jiang, G.Y. Source parameters of the 2016–2017 central Italy earthquake sequence from the Sentinel-1, Alos-2 and GPS data. Remote Sens. 2017, 9, 1182. [Google Scholar] [CrossRef] [Green Version]
- Zheng, M.N.; Deng, K.Z.; Fan, H.D.; Du, S. Monitoring and analysis of surface deformation in mining area based on InSAR and grace. Remote Sens. 2018, 10, 1392. [Google Scholar] [CrossRef] [Green Version]
- Fan, H.D.; Gu, W.; Qin, Y.; Xue, J.Q.; Chen, B.Q. A model for extracting large deformation mining subsidence using D-InSAR technique and probability integral method. Trans. Nonferrous Met. Soc. China 2014, 24, 1242–1247. [Google Scholar] [CrossRef]
- Bu, P.; Li, C.K.; Liao, M.G.; Yang, W.T.; Zhu, C.G.; Fang, J. An approach for estimating underground-goaf boundaries based on combining DInSAR with a graphical method. Adv. Civ. Eng. 2020, 2020, 9375056. [Google Scholar]
- Hu, Z.; Ge, L.L.; Li, X.J.; Zhang, K.; Zhang, L. An underground-mining detection system based on DInSAR. IEEE Trans. Geosci. Remote Sens. 2013, 51, 615–625. [Google Scholar] [CrossRef]
- Xia, Y.P.; Wang, Y.J. InSAR-and PIM-based inclined goaf determination for illegal mining detection. Remote Sens. 2020, 12, 3884. [Google Scholar] [CrossRef]
- Du, S.; Wang, Y.J.; Zheng, M.N.; Zhou, D.W.; Xia, Y.P. Goaf locating based on InSAR and probability integration method. Remote Sens. 2019, 11, 812. [Google Scholar] [CrossRef] [Green Version]
- Wang, L.; Jiang, K.G.; Wei, T.; Jiang, C.; Zha, J.F.; Chi, S.S. Estimation of parameters of probability integral method model based on improved fireworks algorithm. Surv. Rev. 2020, 53, 366–382. [Google Scholar] [CrossRef]
- Li, P.X.; Peng, D.; Tan, Z.X.; Deng, K.Z. Study of probability integration method parameter inversion by the genetic algorithm. Int. J. Min. Sci. Technol. 2017, 27, 1073–1079. [Google Scholar] [CrossRef]
- Yang, J.Y.; Liu, C.; Chen, T.Y.; Zhang, Y.M. The invasive weed optimization-based inversion of parameters in probability integral model. Arab. J. Geosci. 2019, 12, 424. [Google Scholar] [CrossRef]
- Ferretti, A.; Fumagalli, A.; Novali, F.; Prati, C.; Rocca, F.; Rucci, A. A new algorithm for processing interferometric data-stacks: SqueeSAR. IEEE Trans. Geosci. Remote Sens. 2011, 49, 3460–3470. [Google Scholar] [CrossRef]
- Jiang, M.; Ding, X.L.; Hanssen, R.F.; Malhotra, R.; Chang, L. Fast statistically homogeneous pixel selection for covariance matrix estimation for multitemporal InSAR. IEEE Trans. Geosci. Remote Sens. 2015, 53, 1213–1224. [Google Scholar] [CrossRef]
- Cao, N.; Lee, H.; Jung, H.C. A phase-decomposition-based PSInSAR processing method. IEEE Trans. Geosci. Remote Sens. 2016, 54, 1074–1090. [Google Scholar] [CrossRef]
- Berardino, P.; Fornaro, G.; Lanari, R.; Sansosti, E. A new algorithm for surface deformation monitoring based on small baseline differential SAR interferograms. IEEE Trans. Geosci. Remote Sens. 2002, 40, 2375–2383. [Google Scholar] [CrossRef] [Green Version]








| Parameter | Simulated | Estimated | Absolute Error | Relative Error |
|---|---|---|---|---|
| D1 (m) | 1000 | 999.75 | 0.25 | 0.03% |
| D2 (m) | 500 | 501.67 | 1.67 | 0.33% |
| Xc (m) | 1013 | 1010.70 | 2.30 | - |
| Yc (m) | 1000 | 999.20 | 0.80 | - |
| H (m) | 900 | 893.50 | 6.50 | 0.72% |
| φn (°) | 90 | 90.00 | 0.00 | - |
| α (°) | 25 | 24.47 | 0.53 | 2.11% |
| m (m) | 6 | 5.93 | 0.07 | 1.21% |
| q | 0.75 | 0.75 | 0.00 | 0.42% |
| b | 0.35 | 0.35 | 0.00 | 0.33% |
| tanβ | 2.24 | 2.23 | 0.01 | 0.45% |
| Serial Number | Date | Vertical Baseline/m | Time Baseline/Day |
|---|---|---|---|
| 1 | 4 November 2017 | 0 | 0 |
| 2 | 16 November 2017 | 21.33 | 12 |
| 3 | 28 November 2017 | 90.05 | 24 |
| 4 | 10 December 2017 | 49.24 | 36 |
| 5 | 26 December 2017 | 42.51 | 48 |
| 6 | 3 January 2018 | 59.73 | 60 |
| 7 | 15 January 2018 | 1.00 | 72 |
| 8 | 27 January 2018 | 38.52 | 84 |
| 9 | 8 February 2018 | 99.09 | 96 |
| 10 | 20 February 2018 | 87.94 | 108 |
| 11 | 4 March 2018 | 71.14 | 120 |
| 12 | 28 March 2018 | 36.35 | 144 |
| Parameter | Simulated | Estimated | Absolute Error | Relative Error |
|---|---|---|---|---|
| D1 (m) | 437 | 461.90 | 24.90 | 5.70% |
| D2 (m) | 160 | 186.57 | 26.57 | 16.61% |
| Xc (m) | 395 | 351.97 | 43.03 | - |
| Yc (m) | 265 | 229.02 | 35.98 | - |
| H (m) | 946 | 951.89 | 5.89 | 0.62% |
| φn (°) | 254 | 262.04 | 8.04 | - |
| α (°) | 23 | 22.25 | 0.75 | 3.28% |
| m (m) | 2.75 | 2.74 | 7.89 | 0.29% |
| q | 0.83 | 0.79 | 0.04 | 4.56% |
| b | 0.3 | 0.22 | 0.08 | 26.67% |
| tanβ | 1.8 | 1.35 | 0.45 | 24.98% |
| Parameters | Simulated | Estimated | Absolute Error | Relative Error |
|---|---|---|---|---|
| D1 (m) | 1000 | 999.88 | 0.12 | 0.01% |
| D2 (m) | 500 | 499.23 | 0.77 | 0.15% |
| Xc (m) | 1013 | 1013.45 | 0.45 | - |
| Yc (m) | 1000 | 1000.08 | 0.08 | - |
| H (m) | 900 | 901.15 | 1.15 | 0.13% |
| φn (°) | 90 | 90.00 | 0.00 | - |
| α (°) | 25 | 25.21 | 0.21 | 0.85% |
| m (m) | 6 | 0.03 | 0.03 | 0.53% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, T.; Zhang, H.; Fan, H.; Zheng, C.; Liu, J. Position Inversion of Goafs in Deep Coal Seams Based on DS-InSAR Data and the Probability Integral Methods. Remote Sens. 2021, 13, 2898. https://doi.org/10.3390/rs13152898
Li T, Zhang H, Fan H, Zheng C, Liu J. Position Inversion of Goafs in Deep Coal Seams Based on DS-InSAR Data and the Probability Integral Methods. Remote Sensing. 2021; 13(15):2898. https://doi.org/10.3390/rs13152898
Chicago/Turabian StyleLi, Tengteng, Hongzhen Zhang, Hongdong Fan, Chunliu Zheng, and Jiuli Liu. 2021. "Position Inversion of Goafs in Deep Coal Seams Based on DS-InSAR Data and the Probability Integral Methods" Remote Sensing 13, no. 15: 2898. https://doi.org/10.3390/rs13152898