Regional Assessments of Surface Ice Elevations from Swath-Processed CryoSat-2 SARIn Data
Abstract
:1. Introduction
2. Data and Regions of Interest
2.1. CS2 Data
2.2. Airborne-Laser-Scanner Data over Austfonna Ice Cap
2.3. Airborne X-Band Radar Data over Petermann Glacier
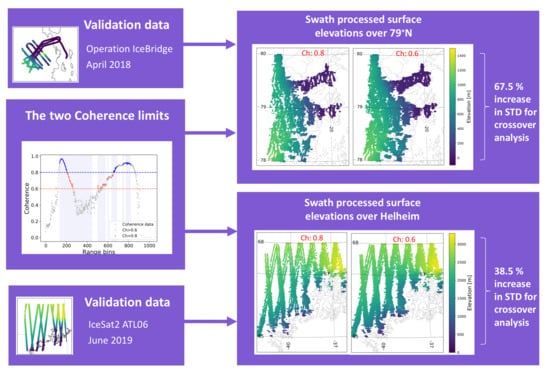
2.4. Operation Icebridge Airborne Topographic Mapper (ATM) Data over Nioghalvfjerdsfjorden Glacier
2.5. ICESat-2 Laser Data over Helheim Glacier
3. Swath Processing
4. Validation Methods
5. Results
6. Discussion
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| ALS | Airbornelaser-scanner data |
| ATLAS | Advanced Topographic Laser Altimeter System |
| ATM | Airborne Topographic Mapper |
| CryoVEx | Cryosat Validation Experiment |
| CS2 | CryoSat-2 |
| DEM | Digital elevation model |
| DTU | Danish Technical University |
| ESA | European Space Agency |
| IS2 | ICESat-2 |
| LRM | Low-resolution mode |
| OIB | Operation ICEbridge |
| POCA | Point of closest approach |
| SAR | Synthetic aperture radar |
| SARIn | interferometric SAR |
| SIRAL | Synthetic Aperture Interferometric Radar Altimeter |
| STD | Standard deviation |
References
- Wingham, D.J.; Francis, C.R.; Baker, S.; Bouzinac, C.; Brockley, D.; Cullen, R.; de Chateau-Thierry, P.; Laxon, S.W.; Mallow, U.; Mavrocordatos, C.; et al. CryoSat: A mission to determine the fluctuations in Earth’s land and marine ice fields. Adv. Space Res. 2006, 37, 841–871. [Google Scholar] [CrossRef]
- Sørensen, L.S.; Simonsen, S.B.; Forsberg, R.; Stenseng, L.; Skourup, H.; Kristensen, S.S.; Colgan, W. Circum-greenland, ice-thickness measurements collected during PROMICE airborne surveys in 2007, 2011 and 2015. Geol. Surv. Den. Greenl. Bull. 2018, 41, 79–82. [Google Scholar]
- Foresta, L.; Gourmelen, N.; Pálsson, F.; Nienow, P.; Björnsson, H.; Shepherd, A. Surface Elevation Change and Mass Balance Of Icelandic Ice Caps Derived From Swath Mode CryoSat-2 Altimetry. Geophys. Res. Lett. 2016, 1–8. [Google Scholar] [CrossRef] [Green Version]
- Shepherd, A.; Ivins, E.; Rignot, E.; Smith, B.; Van Den Broeke, M.; Velicogna, I.; Whitehouse, P.; Briggs, K.; Joughin, I.; Krinner, G.; et al. Mass balance of the Antarctic Ice Sheet from 1992 to 2017. Nature 2018, 558, 219–222. [Google Scholar] [CrossRef] [Green Version]
- Shepherd, A.; Ivins, E.; Rignot, E.; Smith, B.; van den Broeke, M.; Velicogna, I.; Whitehouse, P.; Briggs, K.; Joughin, I.; Krinner, G.; et al. Mass balance of the Greenland Ice Sheet from 1992 to 2018. Nature 2020, 579, 233–239. [Google Scholar] [CrossRef]
- McMillan, M.; Shepherd, A.; Muir, A.; Gaudelli, J.; Hogg, A.E.; Cullen, R. Assessment of CryoSat-2 interferometric and non-interferometric SAR altimetry over ice sheets. Adv. Space Res. 2017, 62, 1281–1291. [Google Scholar] [CrossRef]
- Helm, V.; Humbert, A.; Miller, H. Elevation and elevation change of Greenland and Antarctica derived from CryoSat-2. Cryosphere 2014, 8, 1539–1559. [Google Scholar] [CrossRef] [Green Version]
- Slater, T.; Lawrence, I.R.; Otosaka, I.N.; Shepherd, A.; Gourmelen, N.; Jakob, L.; Tepes, P.; Gilbert, L. Review Article: Earth’s ice imbalance. Cryosphere Discuss. 2021, 15, 233–246. [Google Scholar] [CrossRef]
- Simonsen, S.B.; Barletta, V.R.; Colgan, W.; Sørensen, L.S. Greenland Ice Sheet mass balance (1992–2020) from calibrated radar altimetry. Geophys. Res. Lett. 2021, 48. [Google Scholar] [CrossRef]
- Hawley, R.L.; Shepherd, A.; Cullen, R.; Helm, V.; Wingham, D.J. Ice-sheet elevations from across-track processing of airborne interferometric radar altimetry. Geophys. Res. Lett. 2009, 36, 1–5. [Google Scholar] [CrossRef] [Green Version]
- Gourmelen, N.; Escorihuela, M.J.; Shepherd, A.; Foresta, L.; Muir, A.; Garcia-Mondéjar, A.; Roca, M.; Baker, S.G.; Drinkwater, M.R. CryoSat-2 swath interferometric altimetry for mapping ice elevation and elevation change. Adv. Space Res. 2018, 62, 1226–1242. [Google Scholar] [CrossRef] [Green Version]
- Gray, L.; Burgess, D.; Copland, L.; Cullen, R.; Galin, N.; Hawley, R.; Helm, V. Interferometric swath processing of Cryosat data for glacial ice topography. Cryosphere 2013, 7, 1857–1867. [Google Scholar] [CrossRef] [Green Version]
- Gray, L.; Burgess, D.; Copland, L.; Demuth, M.N.; Dunse, T.; Langley, K.; Schuler, T.V. CryoSat-2 delivers monthly and inter-annual surface elevation change for Arctic ice caps. Cryosphere 2015, 9, 1895–1913. [Google Scholar] [CrossRef] [Green Version]
- McMillan, M.; Corr, H.; Shepherd, A.; Ridout, A.; Laxon, S.; Cullen, R. Three-dimensional mapping by CryoSat-2 of subglacial lake volume changes. Geophys. Res. Lett. 2013, 40, 4321–4327. [Google Scholar] [CrossRef] [Green Version]
- Levinsen, J.F.; Simonsen, S.B.; Sørensen, L.S. Altimetry Data Over Ice Sheets. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 3158–3163. [Google Scholar] [CrossRef]
- Hurkmans, R.T.; Bamber, J.L.; Griggs, J.A. Brief communication: “Importance of slope-induced error correction in volume change estimates from radar altimetry”. Cryosphere 2012, 6, 447–451. [Google Scholar] [CrossRef] [Green Version]
- Nilsson, J.; Sandberg Sørensen, L.; Barletta, V.R.; Forsberg, R. Mass changes in Arctic ice caps and glaciers: Implications of regionalizing elevation changes. Cryosphere 2015, 9, 139–150. [Google Scholar] [CrossRef] [Green Version]
- Hurkmans, R.T.; Bamber, J.L.; Srensen, L.S.; Joughin, I.R.; Davis, C.H.; Krabill, W.B. Spatiotemporal interpolation of elevation changes derived from satellite altimetry for Jakobshavn Isbr, Greenland. J. Geophys. Res. Earth Surf. 2012, 117, 1–16. [Google Scholar] [CrossRef] [Green Version]
- Strößenreuther, U.; Horwath, M.; Schröder, L. How Different Analysis and Interpolation Methods Affect the Accuracy of Ice Surface Elevation Changes Inferred from Satellite Altimetry. Math. Geosci. 2020, 52, 499–525. [Google Scholar] [CrossRef] [Green Version]
- Foresta, L.; Gourmelen, N.; Weissgerber, F.; Nienow, P.; Williams, J.J.; Shepherd, A.; Drinkwater, M.R.; Plummer, S. Heterogeneous and rapid ice loss over the Patagonian Ice Fields revealed by CryoSat-2 swath radar altimetry. Remote Sens. Environ. 2018, 211, 441–455. [Google Scholar] [CrossRef]
- Garcia-Mondéjar, A.; Gourmelen, N.; Escorihuela, M.J.; Roca, M.; Shepherd, A.; Plummer, S. Multisurface Retracker for Swath Processing of Interferometric Radar Altimetry. IEEE Geosci. Remote Sens. Lett. 2019, 16, 1839–1843. [Google Scholar] [CrossRef]
- Garcia-mond, A.; Scagliola, M.; Gourmelen, N.; Bouffard, J. Roll Calibration for CryoSat-2: A Comprehensive Approach. Remote Sens. 2021, 13, 302. [Google Scholar] [CrossRef]
- ESA. CryoSat-2 Product Handbook Baseline D 1.1, C2-LI-ACS-ESL-5319; Technical Report; ESA: Frascati, Italy, 2019. [Google Scholar]
- Krieger, L.; Strößenreuther, U.; Helm, V.; Floricioiu, D.; Horwath, M. Synergistic use of single-pass interferometry and radar altimetry to measure mass loss of NEGIS outlet glaciers between 2011 and 2014. Remote Sens. 2020, 12, 996. [Google Scholar] [CrossRef] [Green Version]
- Atkinson, P.M. Downscaling in remote sensing. Int. J. Appl. Earth Obs. Geoinf. 2013, 22, 106–114. [Google Scholar] [CrossRef]
- European Space Agency; Mullar Space Science Laboratory. CryoSat Product Handbook; Technical Report April; ESRIN-ESA and Mullard Space Science Laboratory—University College: London, UK; Rome, Italy, 2012. [Google Scholar]
- Moholdt, G.; Kääb, A. A new DEM of the Austfonna ice cap by combining differential SAR interferometry with icesat laser altimetry. Pol. Res. 2012, 31, 1–11. [Google Scholar] [CrossRef] [Green Version]
- Wingham, D.; Forsberg, R.; Laxon, S.; Lemke, P.; Miller, H.; Raney, K.; Sandven, S.; Vincent, P.; Rebhan, H. CryoSat Calibration and Validiation Concept; Technical Report November; ESA/CPOM; Centre for Polar Observation and Modelling Department of Space and Climate Physics, University College London: London, UK, 2001. [Google Scholar]
- Sørensen, L.S.; Simonsen, S.B.; Langley, K.; Gray, L.; Helm, V.; Nilsson, J.; Stenseng, L.; Skourup, H.; Forsberg, R.; Davidson, M.W. Validation of CryoSat-2 SARIn data over Austfonna ice cap using airborne laser scanner measurements. Remote Sens. 2018, 10, 1354. [Google Scholar] [CrossRef] [Green Version]
- Meloni, M.; Bouffard, J.; Parrinello, T.; Dawson, G.; Garnier, F.; Helm, V.; Di Bella, A.; Hendricks, S.; Ricker, R.; Webb, E.; et al. CryoSat Ice Baseline-D Validation and Evolutions. Cryosphere 2019, 14, 1889–1907. [Google Scholar] [CrossRef]
- Fugro. GeoSAR Product Handbook; Technical Report May; Fugro EarthData, Inc.: Frederick, MD, USA, 2009. [Google Scholar]
- Mayer, C.; Schaffer, J.; Hattermann, T.; Floricioiu, D.; Krieger, L.; Dodd, P.A.; Kanzow, T.; Licciulli, C.; Schannwell, C. Large ice loss variability at Nioghalvfjerdsfjorden Glacier, Northeast-Greenland. Nat. Commun. 2018, 9, 2768. [Google Scholar] [CrossRef] [Green Version]
- Studinger, M. Operation IceBridge ATM L2 Icessn Elevation Data, Slope, and Roughness, Version 2; 2014, Updated 2020; [INioghalvfjerdfjorden Glacier March 22 and 28, and April 3, 2017]; NASA National Snow and Ice Data Center Distributed Active Archive Center: Boulder, CO, USA, 2014. [CrossRef]
- Howat, I.M.; Joughin, I.; Tulaczyk, S.; Gogineni, S. Rapid retreat and acceleration of Helheim Glacier, east Greenland. Geophys. Res. Lett. 2005, 32, 1–4. [Google Scholar] [CrossRef] [Green Version]
- Smith, B.; Hancock, D.; Harbeck, K.; Roberts, L.; Neumann, T.; Brunt, K.; Fricker, H.; Gardner, A.; Siegfried, M.; Adusumilli, S.; et al. Algorithm Theoretical Basis Document (ATBD) for Land Ice Along-Track Height Product (ATL06); Technical Report; NASA/University of Washington Applied Physics Lab: Seattle, WA, USA, 2019. [CrossRef]
- Nilsson, J.; Gardner, A.; Sørensen, L.S.; Forsberg, R. Improved retrieval of land ice topography from CryoSat-2 data and its impact for volume-change estimation of the Greenland Ice Sheet. Cryosphere 2016, 10, 2953–2969. [Google Scholar] [CrossRef] [Green Version]
- ESA. ENVISAT RA2/MWR Product Handbook; European Space Agency: Paris, France, 2007; p. 204. [Google Scholar]
- Porter, C.; Morin, P.; Howat, I.; Noh, M.J.; Bates, B.; Peterman, K.; Keesey, S.; Schlenk, M.; Gardiner, J.; Tomko, K.; et al. ArcticDEM [Date Accessed 03-01-2020]; Technical Report; Polar Geospatial Center (PGC), Harvard Dataverse: Minneapolis, MN, USA, 2018. [Google Scholar] [CrossRef]
- Consortium RGI. Randolph Glacier Inventory—A Dataset of Global Glacier Outlines: Version 6.0: Technical Report, Global Land Ice Measurements from Space, Colorado; Technical Report; Digital Media: Boulder, CO, USA, 2017. [Google Scholar] [CrossRef]
- Dunse, T.; Schellenberger, T.; Hagen, J.O.; Kääb, A.; Schuler, T.V.; Reijmer, C.H. Glacier-surge mechanisms promoted by a hydro-thermodynamic feedback to summer melt. Cryosphere 2015, 9, 197–215. [Google Scholar] [CrossRef] [Green Version]
- Brunt, K.M.; Smith, B.E.; Sutterley, T.C.; Kurtz, N.T.; Neumann, T.A. Comparisons of Satellite and Airborne Altimetry With Ground-Based Data From the Interior of the Antarctic Ice Sheet. Geophys. Res. Lett. 2021, 48, 1–9. [Google Scholar] [CrossRef]
- Otosaka, I.N.; Shepherd, A.; Casal, T.G.; Coccia, A.; Davidson, M.; Di Bella, A.; Fettweis, X.; Forsberg, R.; Helm, V.; Hogg, A.E.; et al. Surface Melting Drives Fluctuations in Airborne Radar Penetration in West Central Greenland. Geophys. Res. Lett. 2020, 47. [Google Scholar] [CrossRef]





| Study Region | Period | Instrument | |
|---|---|---|---|
| A | Austfonna ice cap | 1–30 April 2016 | ALS |
| B | Petermann glacier | 1–30 April 2014 | X-band Radar |
| C | Nioghalvfjerdsfjorden glacier | 1–30 April 2018 | OIB ATM |
| D | Helheim glacier | 9–24 June 2019 | ICESat-2 |
| Area | Coherence Threshold | Crossover Points | Median [m] | Standard Deviation | Instrument | |
|---|---|---|---|---|---|---|
| Intra-mission | Petermann | 0.8 | 41,712 | −0.003 | 7.12 | CS2 |
| 0.6 | 66,104 | 0.03 | 9.50 (33.4%) | |||
| Helheim | 0.8 | 13,140 | 0.07 | 7.18 | CS2 | |
| 0.6 | 28,138 | 0.03 | 10.84 (50.9%) | |||
| 79 N | 0.8 | 21,659 | −0.03 | 10.46 | CS2 | |
| 0.6 | 39,002 | −0.02 | 14.01 (33.9%) | |||
| Austfonna | 0.8 | 15,703 | −0.06 | 8.63 | CS2 | |
| 0.6 | 25,139 | 0.04 | 13.78 (64.8%) | |||
| External-mission | Petermann | 0.8 | 270,612 | 1.66 | 6.35 | X-band |
| 0.6 | 178,432 | 1.61 | 8.56 (34.8%) | |||
| Helheim | 0.8 | 9397 | −0.15 | 7.55 | IS2 | |
| 0.6 | 15,521 | −0.3 | 10.46 (38.5%) | |||
| 79 N | 0.8 | 4171 | −1.19 | 10.41 | ALS | |
| 0.6 | 6376 | −1.13 | 17.42 (67.3%) | |||
| Austfonna | 0.8 | 3800 | −1.44 | 8.28 | ALS | |
| 0.6 | 5573 | −1.48 | 10.83 (30.7%) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Andersen, N.H.; Simonsen, S.B.; Winstrup, M.; Nilsson, J.; Sørensen, L.S. Regional Assessments of Surface Ice Elevations from Swath-Processed CryoSat-2 SARIn Data. Remote Sens. 2021, 13, 2213. https://doi.org/10.3390/rs13112213
Andersen NH, Simonsen SB, Winstrup M, Nilsson J, Sørensen LS. Regional Assessments of Surface Ice Elevations from Swath-Processed CryoSat-2 SARIn Data. Remote Sensing. 2021; 13(11):2213. https://doi.org/10.3390/rs13112213
Chicago/Turabian StyleAndersen, Natalia Havelund, Sebastian Bjerregaard Simonsen, Mai Winstrup, Johan Nilsson, and Louise Sandberg Sørensen. 2021. "Regional Assessments of Surface Ice Elevations from Swath-Processed CryoSat-2 SARIn Data" Remote Sensing 13, no. 11: 2213. https://doi.org/10.3390/rs13112213