Skills of Thunderstorm Prediction by Convective Indices over a Metropolitan Area: Comparison of Microwave and Radiosonde Data
Abstract
:1. Introduction
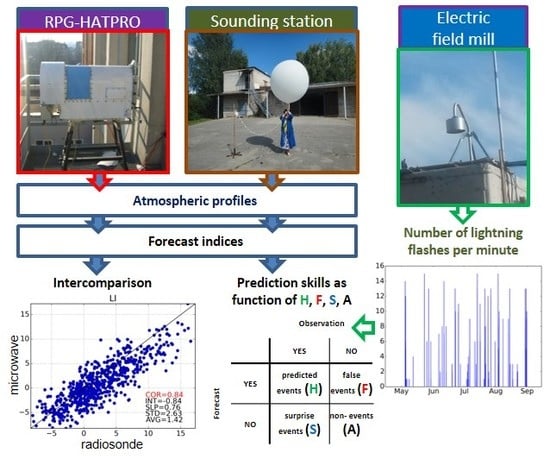
2. Materials and Methods
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Anquetin, S.; Yates, E.; Ducrocq, V.; Samouillan, S.; Chancibault, K.; Davolio, S.; Accadia, C.; Casaioli, M.; Mariani, S.; Ficca, G.; et al. The 8 and 9 September 2002 flash flood event in France: A model intercomparison. Nat. Hazards Earth Syst. Sci. 2005, 5, 741–754. [Google Scholar] [CrossRef]
- Meißner, C.; Kalthoff, N.; Kunz, M.; Adrian, G. Initiation of shallow convection in the Black Forest Mountains. Atmos. Res. 2007, 86, 42–60. [Google Scholar] [CrossRef]
- Rajeevan, M.; Kesarkar, A.; Thampi, S.B.; Rao, T.N.; Radhakrishna, B.; Rajasekhar, M. Sensitivity of WRF cloud microphysics to simulations of a severe thunderstorm event over southeast India. Ann. Geophys. 2010, 28, 603–619. [Google Scholar] [CrossRef]
- Showalter, A.K. A stability index for forecasting thunderstorms. Bull. Am. Meteorol. Soc. 1947, 34, 250–252. [Google Scholar] [CrossRef] [Green Version]
- Fawbush, E.J.; Miller, R.C. A Basis for Forecasting PeakWind Gusts in Non-Frontal Thunderstorms. Bull. Am. Meteorol. Soc. 1954, 35, 14–19. [Google Scholar] [CrossRef] [Green Version]
- Galway, J.G. The lifted index as a predictor of latent instability. Bull. Am. Meteorol. Soc. 1956, 37, 528–529. [Google Scholar] [CrossRef] [Green Version]
- De Coning, E.; Koenig, M.; Olivier, J. The combined instability index: A new very-short range convection forecasting technique for southern Africa. Meteorol. Appl. 2011, 18, 421–439. [Google Scholar] [CrossRef]
- Jürgen Grieser, Convection Parameters. 26 June 2012. Available online: http://www.juergen-grieser.de/ConvectionParameters/ConvectionParameters.pdf (accessed on 16 November 2019).
- Andersson, T.; Andersson, M.; Jacobsson, C.; Nilsson, S. Thermodynamic indices for forecasting thunderstorms in southern Sweden. Meteorol. Mag. 1989, 116, 141–146. [Google Scholar]
- Haklander, A.J.; Van Delden, A. Thunderstorm predictors and their forecast skill for the Netherlands. Atmos. Res. 2003, 67–68, 273–299. [Google Scholar] [CrossRef]
- Manzato, A. A climatology of instability indices derived from Friuli Venezeilia Giulia soundings using three different methods. Atmos. Res. 2003, 67, 417–454. [Google Scholar] [CrossRef]
- Manzato, A. The use of sounding-derived indices for a neural network short-term thunderstorm forecast. Weather Forecast. 2005, 20, 896–917. [Google Scholar] [CrossRef]
- Kunz, M. The skill of convective parameters and indices to predict isolated and severe thunderstorms. Nat. Hazards Earth Syst. Sci. 2007, 7, 327–342. [Google Scholar] [CrossRef] [Green Version]
- Holtslag, M.C.; Steeneveld, G.J.; Holtslag, A.A.M. Fog forecasting: “old fashioned” semi-empirical methods from radio sounding observations versus “modern” numerical models. In Proceedings of the 5th International Conference on Fog, Fog Collection and Dew (FOGDEW2010), Münster, Germany, 25–30 July 2010; Available online: http://meetingorganizer.copernicus.org/FOGDEW2010/FOGDEW2010-69.pdf (accessed on 16 November 2019).
- Kuhlman, C.J. Evaluation of Convective Wind Forecasting Methods During High Wind Events. Master’s Thesis, Naval Postgraduate School, Monterey, CA, USA, 2006. [Google Scholar]
- Gijben, M.; Dyson, L.L.; Loots, M.T. A statistical scheme to forecast the daily lightning threat over southern Africa using the Unified Model. Atmos. Res. 2017, 194, 78–88. [Google Scholar] [CrossRef]
- Marinaki, A.; Spiliotopoulos, M.; Michalopoulou, H. Evaluation of atmospheric instability indices in Greece. Adv. Geosci. 2006, 7, 131–135. [Google Scholar] [CrossRef] [Green Version]
- Koenig, M.; de Coning, E. The MSG Global Instability Indices product and its use as a nowcasting tool. Weather Forecast. 2009, 24, 272–285. [Google Scholar] [CrossRef]
- Güldner, J. A model-based approach to adjust microwave observations for operational applications: Results of a campaign at Munich Airport in winter 2011/2012. Atmos. Meas. Technol. 2013, 6, 2879–2891. [Google Scholar] [CrossRef]
- Cimini, D.; Rizi, V.; Di Girolamo, P.; Marzano, F.S.; Macke, A.; Pappalardo, G.; Richter, A. Overview: Tropospheric profiling: State of the art and future challenges – introduction to the AMT special issue. Atmos. Meas. Technol. 2014, 7, 2981–2986. [Google Scholar] [CrossRef]
- Ware, R.; Cimini, D.; Campos, E.; Giuliani, G.; Albers, S.; Nelson, M.; Koch, S.E.; Joe, P.; Cober, S. Thermodynamic and liquid profiling during the 2010 Winter Olympics. Atmos. Res. 2013, 132–133, 278–290. [Google Scholar] [CrossRef]
- Chan, P.W. Performance and application of a multiwavelength, ground-based microwave radiometer in intense convective weather. Meteorol. Z. 2009, 18, 253–265. [Google Scholar] [CrossRef]
- Chan, P.W.; Hon, K.K. Application of ground-based, multichannel microwave radiometer in the nowcasting of intense convective weather through instability indices of the atmosphere. Meteorol. Z. 2011, 20, 431–440. [Google Scholar] [CrossRef]
- Madhulatha, A.; Rajeevan, M.; Venkat Ratnam, M.; Bhate, J.; Naidu, C.V. Nowcasting severe convective activity over southeast India using ground-based microwave radiometer observations. J. Geophys. Res. Atmos. 2013, 118, 1–13. [Google Scholar] [CrossRef] [Green Version]
- Venkat Ratnam, M.; Durga Santhi, Y.; Rajeevan, M.; Vijaya Bhaskara Rao, S. Diurnal variability of stability indices observed using radiosonde observations over a tropical station: Comparison with microwave radiometer measurements. Atmos. Res. 2013, 124, 21–33. [Google Scholar] [CrossRef]
- Cimini, D.; Nelson, M.; Güldner, J.; Ware, R. Forecast indices from a ground-based microwave radiometer for operational meteorology. Atmos. Meas. Technol. 2015, 8, 315–333. [Google Scholar] [CrossRef] [Green Version]
- Klimenko, V.V.; Mareev, E.A.; Shatalina, M.V.; Shlyugaev, Y.V.; Sokolov, V.V.; Bulatov, A.A.; Denisov, V.P. On Statistical Characteristics of Electric Fields of the Thunderstorm Clouds in the Atmosphere. Radiophys. Quant. Electron. 2014, 56, 778–787. [Google Scholar] [CrossRef]



| Radiosonde Index | TSSmax | λttpTSS | POD | FAR | CSI | HSSmax | λtppHSS | POD | FAR | CSI |
|---|---|---|---|---|---|---|---|---|---|---|
| Perfect/worse forecast | 1/−1 | 1/0 | 0/1 | 1/0 | 1/<0 | 1/0 | 0/1 | 1/0 | ||
| JI | 0.4 | 25.4 | 0.8 | 0.59 | 0.36 | 0.31 | 26 | 0.76 | 0.59 | 0.36 |
| KI | 0.37 | 24.1 | 0.68 | 0.58 | 0.35 | 0.3 | 24.7 | 0.65 | 0.57 | 0.35 |
| SI | 0.36 | 35.5 | 0.83 | 0.63 | 0.35 | 0.29 | 39 | 0.69 | 0.59 | 0.35 |
| TI | 0.34 | 20.4 | 0.76 | 0.62 | 0.34 | 0.28 | 27 | 0.5 | 0.56 | 0.31 |
| TQ | 0.3 | 12.9 | 0.74 | 0.64 | 0.32 | 0.22 | 12.9 | 0.74 | 0.64 | 0.32 |
| ShowI | 0.3 | 4.2 | 0.8 | 0.65 | 0.32 | 0.21 | 4.2 | 0.8 | 0.65 | 0.32 |
| TT | 0.26 | 44.7 | 0.71 | 0.65 | 0.3 | 0.2 | 45.4 | 0.64 | 0.64 | 0.3 |
| MUCAPE | 0.25 | 58.7 | 0.57 | 0.63 | 0.29 | 0.22 | 210.2 | 0.4 | 0.58 | 0.26 |
| EPI | 0.22 | 2.4 | 0.64 | 0.66 | 0.29 | 0.17 | 2.4 | 0.64 | 0.66 | 0.29 |
| LI | 0.18 | −0.52 | 0.43 | 0.63 | 0.24 | 0.17 | −6.85 | 0.4 | 0.63 | 0.24 |
| MDPI | 0.15 | 15.2 | 0.37 | 0.64 | 0.22 | 0.15 | 15.2 | 0.37 | 0.64 | 0.22 |
| CAPE | 0.14 | 164 | 0.41 | 0.66 | 0.23 | 0.15 | 918 | 0.2 | 0.53 | 0.16 |
| KOI | 0.13 | 0.45 | 0.65 | 0.7 | 0.26 | 0.13 | −5.3 | 0.26 | 0.63 | 0.18 |
| CIN | 0.13 | −876 | 0.53 | 0.69 | 0.24 | 0.12 | −100 | 0.22 | 0.61 | 0.16 |
| FT | 0.08 | 2.1 | 0.32 | 0.69 | 0.19 | 0.08 | 2.1 | 0.32 | 0.69 | 0.19 |
| Microwave Index | TSSmax | λttpTSS | POD | FAR | CSI | HSSmax | λttpHSS | POD | FAR | CSI |
|---|---|---|---|---|---|---|---|---|---|---|
| Perfect/worse forecast | 1/−1 | 1/0 | 0/1 | 1/0 | 1/<0 | 1/0 | 0/1 | 1/0 | ||
| ShowI | 0.43 | 2.3 | 0.81 | 0.64 | 0.33 | 0.33 | −0.8 | 0.64 | 0.59 | 0.33 |
| MUCAPE | 0.43 | 6.3 | 0.8 | 0.63 | 0.34 | 0.33 | 56 | 0.64 | 0.58 | 0.34 |
| TT | 0.42 | 47.8 | 0.74 | 0.61 | 0.34 | 0.35 | 48.8 | 0.59 | 0.56 | 0.34 |
| TQ | 0.42 | 15 | 0.78 | 0.63 | 0.33 | 0.33 | 16.7 | 0.57 | 0.57 | 0.33 |
| JI | 0.41 | 27.6 | 0.76 | 0.63 | 0.33 | 0.35 | 30.2 | 0.51 | 0.52 | 0.33 |
| SI | 0.41 | 41.3 | 0.79 | 0.64 | 0.33 | 0.34 | 45.2 | 0.54 | 0.55 | 0.33 |
| KI | 0.4 | 26.3 | 0.72 | 0.62 | 0.33 | 0.32 | 39.3 | 0.55 | 0.57 | 0.32 |
| TI | 0.4 | 25.2 | 0.77 | 0.64 | 0.32 | 0.34 | 32.9 | 0.48 | 0.52 | 0.31 |
| EPI | 0.37 | 2.5 | 0.86 | 0.68 | 0.3 | 0.27 | −2.1 | 0.5 | 0.6 | 0.28 |
| LI | 0.37 | −0.3 | 0.7 | 0.64 | 0.31 | 0.32 | −2.5 | 0.5 | 0.55 | 0.31 |
| CAPE | 0.33 | 335 | 0.6 | 0.63 | 0.3 | 0.31 | 974 | 0.38 | 0.49 | 0.28 |
| KOI | 0.31 | −4.2 | 0.52 | 0.6 | 0.29 | 0.28 | −4.2 | 0.52 | 0.6 | 0.29 |
| FT | 0.31 | 3.5 | 0.68 | 0.67 | 0.28 | 0.23 | 3.35 | 0.64 | 0.66 | 0.28 |
| CIN | 0.29 | −651 | 0.74 | 0.7 | 0.27 | 0.25 | −138 | 0.49 | 0.62 | 0.27 |
| MDPI | 0.29 | 7.5 | 0.62 | 0.66 | 0.28 | 0.22 | 7.5 | 0.62 | 0.66 | 0.28 |
| Index | ΔTmax | ΔHmax | CORs | CORs from [26] |
|---|---|---|---|---|
| ShowI | 0.13 | 0.12 | 0.74 | 0.74 |
| MUCAPE | 0.18 | 0.11 | 0.39 | - |
| TT | 0.16 | 0.15 | 0.68 | 0.74 |
| TQ | 0.12 | 0.11 | 0.75 | 0.80 |
| JI | 0.01 | 0.04 | 0.78 | 0.81 |
| SI | 0.05 | 0.05 | 0.78 | 0.82 |
| KI | 0.03 | 0.02 | 0.81 | 0.82 |
| TI | 0.06 | 0.06 | 0.86 | 0.85 |
| EPI | 0.15 | 0.1 | 0.75 | - |
| LI | 0.19 | 0.15 | 0.84 | 0.92 |
| CAPE | 0.19 | 0.16 | 0.74 | 0.82 |
| KOI | 0.18 | 0.15 | 0.84 | 0.85 |
| FT | 0.23 | 0.15 | 0.56 | 0.77 |
| CIN | 0.16 | 0.13 | 0.86 | 0.21 |
| MDPI | 0.14 | 0.07 | 0.71 | 0.68 |
| Radiosonde index | TSSmax | λttpTSS | POD | FAR | CSI | HSSmax | λttpHSS | POD | FAR | CSI |
|---|---|---|---|---|---|---|---|---|---|---|
| Perfect/worse forecast | 1/−1 | 1/0 | 0/1 | 1/0 | 1/<0 | 1/0 | 0/1 | 1/0 | ||
| TI | 0.36 | 19.1 | 0.82 | 0.68 | 0.3 | 0.31 | 27.7 | 0.51 | 0.57 | 0.3 |
| KI | 0.36 | 22.3 | 0.78 | 0.67 | 0.3 | 0.25 | 24.1 | 0.68 | 0.65 | 0.3 |
| JI | 0.36 | 25.4 | 0.79 | 0.67 | 0.3 | 0.25 | 26.1 | 0.74 | 0.66 | 0.3 |
| SI | 0.34 | 35.2 | 0.84 | 0.69 | 0.29 | 0.24 | 41.5 | 0.55 | 0.64 | 0.28 |
| TQ | 0.33 | 11.4 | 0.9 | 0.7 | 0.29 | 0.22 | 16.4 | 0.41 | 0.62 | 0.24 |
| ShowI | 0.32 | 4.2 | 0.82 | 0.7 | 0.28 | 0.24 | 1.8 | 0.54 | 0.64 | 0.27 |
| EPI | 0.29 | 2.5 | 0.71 | 0.69 | 0.28 | 0.2 | 2.5 | 0.71 | 0.69 | 0.28 |
| TT | 0.28 | 44.7 | 0.73 | 0.7 | 0.27 | 0.22 | 51 | 0.26 | 0.51 | 0.2 |
| LI | 0.28 | 1.6 | 0.71 | 0.7 | 0.27 | 0.22 | −1.8 | 0.34 | 0.6 | 0.23 |
| MUCAPE | 0.26 | 129 | 0.5 | 0.64 | 0.26 | 0.23 | 129 | 0.5 | 0.64 | 0.26 |
| KOI | 0.23 | 0.5 | 0.74 | 0.72 | 0.26 | 0.2 | −4.2 | 0.4 | 0.64 | 0.23 |
| CIN | 0.21 | −876 | 0.6 | 0.71 | 0.24 | 0.18 | −48 | 0.23 | 0.56 | 0.18 |
| MDPI | 0.2 | 9.6 | 0.62 | 0.72 | 0.24 | 0.17 | 15.7 | 0.38 | 0.66 | 0.22 |
| CAPE | 0.19 | 118 | 0.51 | 0.7 | 0.23 | 0.21 | 529 | 0.32 | 0.6 | 0.22 |
| FT | 0.06 | 9.4 | 0.97 | 0.78 | 0.22 | 0.04 | −1.1 | 0.36 | 0.5 | 0.03 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kulikov, M.Y.; Belikovich, M.V.; Skalyga, N.K.; Shatalina, M.V.; Dementyeva, S.O.; Ryskin, V.G.; Shvetsov, A.A.; Krasil’nikov, A.A.; Serov, E.A.; Feigin, A.M. Skills of Thunderstorm Prediction by Convective Indices over a Metropolitan Area: Comparison of Microwave and Radiosonde Data. Remote Sens. 2020, 12, 604. https://doi.org/10.3390/rs12040604
Kulikov MY, Belikovich MV, Skalyga NK, Shatalina MV, Dementyeva SO, Ryskin VG, Shvetsov AA, Krasil’nikov AA, Serov EA, Feigin AM. Skills of Thunderstorm Prediction by Convective Indices over a Metropolitan Area: Comparison of Microwave and Radiosonde Data. Remote Sensing. 2020; 12(4):604. https://doi.org/10.3390/rs12040604
Chicago/Turabian StyleKulikov, Mikhail Yu., Mikhail V. Belikovich, Natalya K. Skalyga, Maria V. Shatalina, Svetlana O. Dementyeva, Vitaly G. Ryskin, Alexander A. Shvetsov, Alexander A. Krasil’nikov, Evgeny A. Serov, and Alexander M. Feigin. 2020. "Skills of Thunderstorm Prediction by Convective Indices over a Metropolitan Area: Comparison of Microwave and Radiosonde Data" Remote Sensing 12, no. 4: 604. https://doi.org/10.3390/rs12040604