Hyperspectral Image Denoising Based on Nonlocal Low-Rank and TV Regularization
Abstract
:1. Introduction
2. Notations and Preliminaries
3. Proposed Model
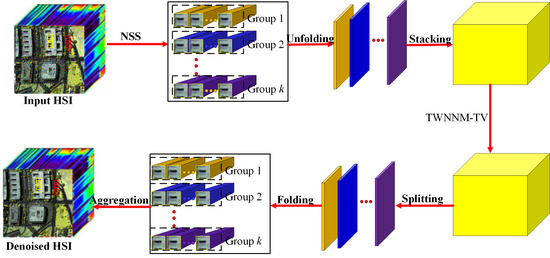
3.1. From WNNM to TWNNM
3.2. Weighted Tensor Total Variation Regularization
3.3. Nonlocal Low-Rank Tensor Construction
3.4. Model Proposal and Optimization
| Algorithm 1 Optimization Process for Proposed Solver |
|
| Output: The restoration result . |
4. Experimental Results and Analysis
4.1. Experiment with Simulated Data
4.2. Real-World Data Experiments
4.2.1. HYDICE Urban Dataset
4.2.2. AVIRIS Salinas Dataset
4.3. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Shomorony, I.; Avestimehr, A.S. Is Gaussian noise the worst-case additive noise in wireless networks? In Proceedings of the 2012 IEEE International Symposium on Information Theory Proceedings (ISIT), Cambridge, MA, USA, 1–6 July 2012. [Google Scholar] [CrossRef]
- Yang, J.; Zhao, Y.; Chan, J.C. Learning and Transferring Deep Joint Spectral–Spatial Features for Hyperspectral Classification. IEEE Trans. Geosci. Remote Sens. 2017, 55, 4729–4742. [Google Scholar] [CrossRef]
- Yi, C.; Zhao, Y.Q.; Chan, J.C.W. Spectral super-resolution for multispectral image based on spectral improvement strategy and spatial preservation strategy. IEEE Trans. Geosci. Remote Sens. 2019. [Google Scholar] [CrossRef]
- Bu, Y.; Zhao, Y.; Xue, J. Hyperspectral and Multispectral Image Fusion via Graph Laplacian-Guided Coupled Tensor Decomposition. IEEE Trans. Geosci. Remote Sens. 2020, 99, 1–15. [Google Scholar] [CrossRef]
- Xue, J.; Zhao, Y.; Liao, W.; Chan, J.C.-W. Hyper-Laplacian Regularized Nonlocal Low-rank Matrix Recovery for Hyperspectral Image Compressive Sensing Reconstruction. Inf. Sci. 2019, 501, 406–420. [Google Scholar] [CrossRef]
- Xue, J.; Zhao, Y.; Liao, W.; Chan, J.-W. Nonlocal Tensor Sparse Representation and Low-Rank Regularization for Hyperspectral Image Compressive Sensing Reconstruction. Remote Sens. 2019, 11, 193. [Google Scholar] [CrossRef] [Green Version]
- Elad, M.; Aharon, M. Image denoising via sparse and redundant representations over learned dictionaries. IEEE Trans. Image Process. 2006, 15, 3736–3745. [Google Scholar] [CrossRef]
- He, W.; Zhang, H.; Zhang, L.; Shen, H. Total-variation-regularized low-rank matrix factorization for hyperspectral image restoration. IEEE Trans. Geosci. Remote Sens. 2016, 54, 178–188. [Google Scholar] [CrossRef]
- Othman, H.; Qian, S.-E. Noise reduction of hyperspectral imagery using hybrid spatial-spectral derivative-domain wavelet shrinkage. IEEE Trans. Geosci. Remote Sens. 2006, 44, 397–408. [Google Scholar] [CrossRef]
- Yuan, Q.; Zhang, L.; Shen, H. Hyperspectral image denoising employing a spectral–spatial adaptive total variation model. IEEE Trans. Geosci. Remote Sens. 2012, 50, 3660–3677. [Google Scholar] [CrossRef]
- Qian, Y.; Ye, M. Hyperspectral imagery restoration using nonlocal spectral-spatial structured sparse representation with noise estimation. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2013, 6, 499–515. [Google Scholar] [CrossRef]
- Wang, Y.; Niu, R.; Yu, X. Anisotropic diffusion for hyperspectral imagery enhancement. IEEE Sens. J. 2010, 10, 469–477. [Google Scholar] [CrossRef]
- Wright, J.; Ganesh, A.; Rao, S.; Peng, Y.; Ma, Y. Robust Principal Component Analysis: Exact Recovery of Corrupted Low-Rank Matrices via Convex Optimization. In Proceedings of the Neural Information Processing Systems 2009, Vancouver, BC, Canada, 6–8 December 2009; pp. 2080–2088. [Google Scholar] [CrossRef]
- Xue, J.; Zhao, Y.; Liao, W.; Chan, J.C.-W. Nonlocal Low-Rank Regularized Tensor Decomposition for Hyperspectral Image Denoising. IEEE Trans. Geosci. Remote Sens. 2019. [Google Scholar] [CrossRef]
- Dong, W.; Shi, G.; Li, X. Nonlocal image restoration with bilateral variance estimation: A low-rank approach. IEEE Trans. Image Process. 2013, 22, 700–711. [Google Scholar] [CrossRef] [PubMed]
- Xue, J.; Zhao, Y.; Liao, W.; Kong, S.G. Joint Spatial and Spectral Low-Rank Regularization for Hyperspectral Image Denoising. IEEE Trans. Geosci. Remote Sens. 2017, 99, 1–19. [Google Scholar] [CrossRef]
- Zheng, Y.; Liu, G.; Sugimoto, S.; Yan, S.; Okutomi, M. Practical Low-Rank Matrix Approximation under Robust L1-Norm. In Proceedings of the 2012 Computer Vision and Pattern Recognition (CVPR), Providence, RI, USA, 16–21 June 2012; pp. 1410–1417. [Google Scholar] [CrossRef]
- Zhang, H.; He, W.; Zhang, L.; Shen, H.; Yuan, Q. Hyperspectral image restoration using low-rank matrix recovery. IEEE Trans. Geosci. Remote Sens. 2013, 52, 4729–4743. [Google Scholar] [CrossRef]
- Gu, S.; Zhang, L.; Zuo, W.; Feng, X. Weighted nuclear norm minimization with application to image denoising. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Columbus, OH, USA, 23–28 June 2014; pp. 2862–2869. [Google Scholar] [CrossRef] [Green Version]
- Gu, S.; Xie, Q.; Meng, D.; Zuo, W.; Feng, X.; Zhang, L. Weighted nuclear norm minimization and its applications to low level vision. Int. J. Comput. Vis. 2017, 121, 183–208. [Google Scholar] [CrossRef]
- Cai, J.; Candes, E.J.; Shen, Z. A singular value thresholding algorithm for matrix completion. SIAM J. Optim. 2010, 20, 1956–1982. [Google Scholar] [CrossRef]
- Wu, Z.; Wang, Q.; Wu, Z.; Shen, Y. Total Variation-Regularized Weighted Nuclear Norm Minimization for Hyperspectral Image Mixed Denoising. J. Electron. Imaging 2016, 25, 13037. [Google Scholar] [CrossRef]
- Du, B.; Huang, Z.; Wang, N.; Zhang, Y.; Jia, X. Joint weighted nuclear norm and total variation regularization for hyperspectral image denoising. Int. J. Remote Sens. 2018, 39, 334–355. [Google Scholar] [CrossRef]
- Kong, X.; Zhao, Y.; Xue, J.; Chan, J.-W. Hyperspectral Image Denoising Using Global Weighted Tensor Norm Minimum and Nonlocal Low-Rank Approximation. Remote Sens. 2019, 11, 2281. [Google Scholar] [CrossRef] [Green Version]
- Wu, Z.; Wang, Q.; Jin, J.; Shen, Y. Structure tensor total variation regularized weighted nuclear norm minimization for hyperspectral image mixed denoising. Signal Process. 2017, 131, 202–219. [Google Scholar] [CrossRef]
- Lefkimmiatis, S.; Roussos, A.; Maragos, P.; Unser, M. Structure tensor total variation. SIAM J. Imaging Sci. 2015, 8, 1090–1122. [Google Scholar] [CrossRef]
- Berchtold, S.; Ertl, B.; Keim, D.A.; Kriegel, H.-P.; Seidl, T. Fast Nearest Neighbor Search in High-Dimensional Space. In Proceedings of the 14th International Conference on Data Engineering, Orlando, FL, USA, 23–27 February 1998; pp. 209–218. [Google Scholar] [CrossRef]
- Kolda, T.G.; Bader, B.W. Tensor decompositions and applications. SIAM Rev. 2009, 51, 455–500. [Google Scholar] [CrossRef]
- Xue, J.; Zhao, Y.; Liao, W.; Chan, J.C.; Kong, S.G. Enhanced Sparsity Prior Model for Low-Rank Tensor Completion. IEEE Trans. Neural Netw. Learn. Syst. 2019, 12, 1–15. [Google Scholar] [CrossRef] [PubMed]
- Boyd, S.; Parikh, N.; Chu, E.; Peleato, B.; Eckstein, J. Distributed optimization and statistical learning via the alternating direction method of multipliers. Found. Trends Mach. Learn. 2011, 3, 1–122. [Google Scholar] [CrossRef]
- Donoho, D.L. De-noising by soft-thresholding. IEEE Trans. Inf. Theory 1995, 41, 613–627. [Google Scholar] [CrossRef] [Green Version]
- Zhang, C.; Hu, W.; Jin, T.; Mei, Z. Nonlocal image denoising via adaptive tensor nuclear norm minimization. Neural Comput. Appl. 2015. [Google Scholar] [CrossRef]
- Rasti, B.; Ulfarsson, M.O.; Ghamisi, P. Automatic hyperspectral image restoration using sparse and low-rank modeling. IEEE Geosci. Remote Sens. Lett. 2017, 14, 2335–2339. [Google Scholar] [CrossRef] [Green Version]
- He, W.; Zhang, H.; Zhang, L.; Shen, H. Hyperspectral Image Denoising via Noise-Adjusted Iterative Low-Rank Matrix Approximation. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 3050–3061. [Google Scholar] [CrossRef]
- Wang, Y.; Peng, J.; Zhao, Q.; Leung, Y.; Zhao, X.-L.; Meng, D. Hyperspectral image restoration via total variation regularized low-rank tensor decomposition. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 11, 1227–1243. [Google Scholar] [CrossRef] [Green Version]
- Available online: http://www.ehu.eus/ccwintco/index.php?title=Hyperspectral_Remote_Sensing_Scenes (accessed on 11 May 2020).
- Wang, Z.; Bovik, A.C.; Sheikh, H.R.; Simoncelli, E.P. Image quality assessment: From error visibility to structural similarity. IEEE Trans. Image Process. 2004, 13, 600–612. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yuhas, R.H.; Goetz, A.F.H.; Boardman, J.W. Discrimination among Semi-Arid Landscape Endmembers Using the Spectral Angle Mapper (SAM) Algorithm. In Proceedings of the 1992 Summaries of the 3rd Annual JPL Airborne Geoscience Workshop, Pasadena, CA, USA, 1–5 June 1992; JPL: Pasadena, CA, USA; pp. 147–149. [Google Scholar]
- Kong, X.; Zhao, Y.; Xue, J.; Chan, J.-W.; Kong, S.G. Global and Local Tensor Sparse Approximation Models for Hyperspectral Image Destriping. Remote Sens. 2020, 12, 704. [Google Scholar] [CrossRef] [Green Version]
- Available online: http://www.tec.army.mil/hypercube (accessed on 11 May 2020).
- Yuan, J. MRI denoising via sparse tensors with reweighted regularization. Appl. Math. Model. 2019, 69, 552–562. [Google Scholar] [CrossRef]
- Turani, Z.; Fatemizadeh, E.; Blumetti, T.; Daveluy, S.; Moraes, A.F.; Chen, W.; Mehregan, D.; Andersen, P.E.; Nasiriavanak, M. Optical Radiomic Signatures Derived from Optical Coherence Tomography Images to Improve Identification of Melanoma. Cancer Res. 2019, 79, 2021–2030. [Google Scholar] [CrossRef] [Green Version]
- Adabi, S.; Rashedi, E.; Clayton, A.; Mohebbi-Kalkhoran, H.; Chen, X.-W.; Conforto, S.; Nasiriavanaki, M. Learnable despeckling framework for optical coherence tomography images. J. Biomed. Opt. 2018, 23, 1–12. [Google Scholar] [CrossRef] [Green Version]
- Eybposh, M.H.; Turani, Z.; Mehregan, D.; Nasiriavanaki, M. Cluster-based filtering framework for speckle reduction in OCT images. Biomed. Opt. Express 2018, 9, 6359–6373. [Google Scholar] [CrossRef]













| Natation | Description |
|---|---|
| x, x, X, | scalar, vector, matrix, tensor |
| xi | i-th entry of a vector x |
| xij | element (i, j) of a matrix X |
| the element in location (i, j, k) of a three-order tensor | |
| Frobenius norm of an N order tensor |
| Variance | Index | Noisy | HyRes | LRTV | LRMR | NAIRLMA | LRTDTV | Proposed |
|---|---|---|---|---|---|---|---|---|
| MPSNR | 26.780 | 42.395 | 41.066 | 42.503 | 43.088 | 43.503 | 49.79 | |
| 10 | MSSIM | 0.6566 | 0.9874 | 0.9958 | 0.9849 | 0.9845 | 0.9976 | 0.9987 |
| MSAM | 0.0789 | 0.0116 | 0.108 | 0.0114 | 0.0104 | 0.0100 | 0.0038 | |
| ERGAS | 91.77 | 16.02 | 20.36 | 15.25 | 14.22 | 15.17 | 7.22 | |
| MPSNR | 20.763 | 37.469 | 38.815 | 36.522 | 38.214 | 41.092 | 43.330 | |
| MSSIM | 0.4366 | 0.9665 | 0.9927 | 0.9472 | 0.9586 | 0.990 | 0.9953 | |
| 20 | MSAM | 0.1565 | 0.0200 | 0.0143 | 0.0227 | 0.0174 | 0.0136 | 0.0090 |
| ERGAS | 183.45 | 28.26 | 25.82 | 30.412 | 25.22 | 19.32 | 14.891 | |
| MPSNR | 17.24 | 34.75 | 35.65 | 32.95 | 34.97 | 37.84 | 40.16 | |
| 30 | MSSIM | 0.3240 | 0.9417 | 0.9863 | 0.8949 | 0.9219 | 0.9685 | 0.9902 |
| MSAM | 0.2316 | 0.0270 | 0.0205 | 0.0343 | 0.0248 | 0.0204 | 0.0127 | |
| ERGAS | 275.15 | 38.30 | 33.94 | 46.10 | 36.15 | 27.44 | 20.48 | |
| MPSNR | 14.741 | 32.860 | 33.798 | 30.418 | 33.105 | 35.017 | 38.012 | |
| 40 | MSSIM | 0.2528 | 0.9150 | 0.9787 | 0.8379 | 0.8933 | 0.931 | 0.9830 |
| MSAM | 0.3037 | 0.0332 | 0.0252 | 0.0461 | 0.0299 | 0.0285 | 0.0157 | |
| ERGAS | 366.98 | 47.708 | 42.389 | 61.367 | 45.078 | 37.76 | 23.67 | |
| MPSNR | 12.80 | 31.44 | 32.10 | 28.51 | 31.22 | 32.76 | 35.78 | |
| MSSIM | 0.2031 | 0.8964 | 0.9697 | 0.7807 | 0.8524 | 0.8846 | 0.9734 | |
| 50 | MSAM | 0.3719 | 0.0385 | 0.0309 | 0.0574 | 0.0367 | 0.0371 | 0.0212 |
| ERGAS | 458.73 | 56.21 | 50.51 | 76.09 | 55.77 | 49.12 | 34.81 | |
| MPSNR | 11.219 | 30.279 | 30.898 | 26.981 | 29.723 | 30.821 | 34.983 | |
| 60 | MSSIM | 0.1688 | 0.8687 | 0.9620 | 0.7259 | 0.8126 | 0.8339 | 0.9649 |
| MSAM | 0.4359 | 0.0438 | 0.0360 | 0.0683 | 0.0432 | 0.0464 | 0.0228 | |
| ERGAS | 550.44 | 64.06 | 59.84 | 91.33 | 66.51 | 61.47 | 37.81 | |
| MPSNR | 9.88 | 29.24 | 29.71 | 25.61 | 28.58 | 29.26 | 32.70 | |
| 70 | MSSIM | 0.1388 | 0.8488 | 0.9514 | 0.6745 | 0.7812 | 0.7806 | 0.9521 |
| MSAM | 0.4964 | 0.0496 | 0.0428 | 0.0800 | 0.0485 | 0.0552 | 0.0321 | |
| ERGAS | 642.04 | 71.60 | 69.80 | 105.44 | 75.02 | 72.97 | 48.95 | |
| MPSNR | 8.717 | 28.459 | 28.787 | 24.572 | 27.582 | 27.939 | 32.202 | |
| 80 | MSSIM | 0.1167 | 0.8262 | 0.9415 | 0.6297 | 0.7465 | 0.7314 | 0.9425 |
| MSAM | 0.5523 | 0.0539 | 0.0472 | 0.0906 | 0.0544 | 0.0646 | 0.0333 | |
| ERGAS | 734.13 | 78.09 | 75.95 | 119.77 | 85.11 | 85.01 | 51.61 | |
| MPSNR | 7.70 | 27.72 | 27.68 | 23.52 | 26.61 | 26.71 | 31.62 | |
| 90 | MSSIM | 0.0992 | 0.7981 | 0.9272 | 0.5856 | 0.7122 | 0.6806 | 0.9288 |
| MSAM | 0.6044 | 0.0592 | 0.0584 | 0.1024 | 0.0606 | 0.0747 | 0.0354 | |
| ERGAS | 825.26 | 84.92 | 86.87 | 135.19 | 95.01 | 97.08 | 54.24 | |
| MPSNR | 6.78 | 27.10 | 26.60 | 22.62 | 25.71 | 25.72 | 31.13 | |
| 100 | MSSIM | 0.0855 | 0.7827 | 0.9118 | 0.5463 | 0.6792 | 0.6396 | 0.9184 |
| MSAM | 0.6528 | 0.0632 | 0.0665 | 0.1136 | 0.0668 | 0.0835 | 0.0362 | |
| ERGAS | 917.09 | 91.87 | 99.68 | 149.93 | 103.87 | 108.51 | 57.96 |
| Method | HyRes | LRMR | LRTV | NAIRLMA | LRTDTV | Proposed |
|---|---|---|---|---|---|---|
| Time (second) | 29 | 0.209 | 483.42 | 439.21 | 942.92 | 587.08 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kong, X.; Zhao, Y.; Xue, J.; Chan, J.C.-W.; Ren, Z.; Huang, H.; Zang, J. Hyperspectral Image Denoising Based on Nonlocal Low-Rank and TV Regularization. Remote Sens. 2020, 12, 1956. https://doi.org/10.3390/rs12121956
Kong X, Zhao Y, Xue J, Chan JC-W, Ren Z, Huang H, Zang J. Hyperspectral Image Denoising Based on Nonlocal Low-Rank and TV Regularization. Remote Sensing. 2020; 12(12):1956. https://doi.org/10.3390/rs12121956
Chicago/Turabian StyleKong, Xiangyang, Yongqiang Zhao, Jize Xue, Jonathan Cheung-Wai Chan, Zhigang Ren, HaiXia Huang, and Jiyuan Zang. 2020. "Hyperspectral Image Denoising Based on Nonlocal Low-Rank and TV Regularization" Remote Sensing 12, no. 12: 1956. https://doi.org/10.3390/rs12121956