Sub-Nyquist SAR via Quadrature Compressive Sampling with Independent Measurements
Abstract
:1. Introduction
Notation
2. SAR Imaging and Sub-Nyquist SAR Model
2.1. SAR Imaging
2.2. Sub-Nyquist SAR
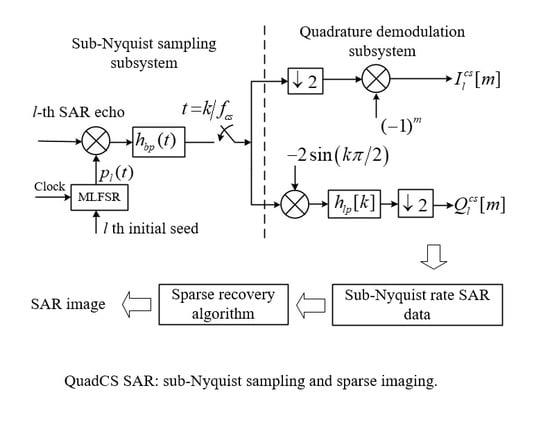
3. Quadrature Compressive Sampling for SAR with Independent Measurements
3.1. Sampling SAR Echoes via QuadCS
3.2. Frequency-Domain Representation
3.3. Remarks
4. Fast Sparse Imaging with QuadCS Measurements
4.1. Fast Matrix-Vector Products
4.2. FISTA-Based Fast Imaging Algorithm
| Algorithm 1: Fast sparse imaging with QuadCS measurements |
| Input: Operators , and their adjoints; QuadCS measurement ; number of iterations ; ; Output: Sparse SAR image ;
|
4.3. Complexity
5. Restricted Isometry Property (RIP) Analysis
6. Simulations
6.1. Simulations with Synthetic Data
6.2. Simulations with Real SAR Data
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| SAR | Synthetic aperture radar |
| RIP | Restricted isometry property |
| CS | Compressive sensing |
| ADC | Analog-to-digital converter |
| MLFSR | Maximal-length linear feedback shift register |
| FFT | Fast Fourier transform |
| PRI | Pulse repetition interval |
| CSA | Chirp scaling algorithm |
| IF | Intermediate frequency |
| DFT | Discrete Fourier transform |
| FISTA | Fast iterative shrinkage-thresholding algorithm |
| BPDN | Basis pursuit denoising |
| RRMSE | Relative root-mean-square error |
Appendix A
Appendix A.1.
Appendix A.2.
Appendix A.3.
References
- Candès, E.J.; Wakin, M.B. An introduction to compressive sampling. IEEE Signal Process Mag. 2008, 25, 21–30. [Google Scholar] [CrossRef]
- Ender, J.H.G. On compressive sensing applied to radar. Signal Process. 2010, 90, 1402–1414. [Google Scholar] [CrossRef]
- Cetin, M.; Stojanovic, I.; Onhon, O.; Varshney, K.; Samadi, S.; Karl, W.C.; Willsky, A.S. Sparsity-driven synthetic aperture radar imaging: Reconstruction, autofocusing, moving targets, and compressed sensing. IEEE Signal Process Mag. 2014, 31, 27–40. [Google Scholar] [CrossRef]
- Aberman, K.; Eldar, Y.C. Sub-Nyquist SAR via Fourier domain range-Doppler processing. IEEE Trans. Geosci. Remote Sens. 2017, 55, 6228–6244. [Google Scholar] [CrossRef]
- Dong, X.; Zhang, Y. A novel compressive sensing algorithm for SAR imaging. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 708–720. [Google Scholar] [CrossRef]
- Kirolos, S.; Laska, J.; Wakin, M.; Duarte, M.; Baron, D.; Ragheb, T.; Massoud, Y.; Baraniuk, R. Analog-to-information conversion via random demodulation. In Proceedings of the IEEE Dallas/CAS Workshop on Design, Applications, Integration and Software, Richardson, TX, USA, 29–30 October 2006; pp. 71–74. [Google Scholar]
- Duarte, M.F.; Eldar, Y.C. Structured compressed sensing: From theory to applications. IEEE Trans. Signal Process. 2011, 59, 4053–4085. [Google Scholar] [CrossRef]
- Laska, J.; Kirolos, S.; Massoud, Y.; Baraniuk, R.; Gilbert, A.; Iwen, M.; Strauss, M. Random sampling for analog-to-information conversion of wideband signals. In Proceedings of the IEEE Dallas/CASWorkshop on Design, Applications, Integration and Software, Richardson, TX, USA, 29–30 October 2006; pp. 119–122. [Google Scholar]
- Wakin, M.; Becker, S.; Nakamura, E.; Grant, M.; Sovero, E.; Ching, D.; Yoo, J.; Romberg, J.; Emami-Neyestanak, A.; Candès, E.J. A nonuniform sampler for wideband spectrally-sparse environments. IEEE J. Emerg. Sel. Top. Circuits Syst. 2012, 2, 516–529. [Google Scholar] [CrossRef]
- Xi, F.; Chen, S.; Liu, Z. Quadrature compressive sampling for radar signals. IEEE Trans. Signal Process. 2014, 62, 2787–2802. [Google Scholar]
- Mishali, M.; Eldar, Y.C.; Dounaevsky, O.; Shoshan, E. Xampling: Analog to digital at sub-Nyquist rates. IET Circuits Devices Syst. 2011, 5, 8–20. [Google Scholar] [CrossRef]
- Baransky, E.; Itzhak, G.; Wagner, N.; Shmuel, I.; Shoshan, E.; Eldar, Y.C. Sub-Nyquist radar prototype: Hardware and algorithm. IEEE Trans. Aerosp. Electron. Syst. 2014, 50, 809–822. [Google Scholar] [CrossRef]
- Song, S.; Xu, B.; Yang, J. Ship detection in polarimetric sar images using targets’ sparse property. In Proceedings of the 2016 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Beijing, China, 10–15 July 2016; pp. 5706–5709. [Google Scholar]
- Liu, Y.; Quan, Y.; Li, J.; Zhang, L.; Xing, M. SAR imaging of multiple ships based on compressed sensing. In Proceedings of the 2009 2nd Asian-Pacific Conference on Synthetic Aperture Radar, Xi’an, China, 26–30 October 2009; pp. 112–115. [Google Scholar]
- Mallat, S.G.; Zhang, Z. Matching pursuits with time-frequency dictionaries. IEEE Trans. Signal Process. 1993, 41, 3397–3415. [Google Scholar] [CrossRef] [Green Version]
- Donoho, D.L.; Elad, M. Optimally sparse representation in general (non-orthogonal) dictionaries via l1 minimization. Proc. Nalt. Acad. Sci. USA 2003, 100, 2197–2202. [Google Scholar] [CrossRef]
- Liu, C.; Xi, F.; Chen, S.; Zhang, Y.D.; Liu, Z. Pulse-Doppler signal processing with quadrature compressive sampling. IEEE Trans. Aerosp. Electron. Syst. 2015, 51, 1217–1230. [Google Scholar] [CrossRef]
- Chen, S.; Xi, F.; Liu, Z. A general sequential delay-Doppler estimation scheme for sub-Nyquist pulse-Doppler radar. Signal Process. 2017, 135, 210–217. [Google Scholar] [CrossRef] [Green Version]
- Chen, S.; Xi, F.; Liu, Z. A general and yet efficient scheme for sub-Nyquist radar processing. Signal Process. 2018, 142, 206–211. [Google Scholar] [CrossRef] [Green Version]
- Ho, K.C.; Chan, Y.T.; Inkol, R. A digital quadrature demodulation system. IEEE Trans. Aerosp. Electron. Syst. 1996, 32, 1218–1227. [Google Scholar] [CrossRef]
- Yang, H.; Chen, S.; Xi, F.; Liu, Z. Quadrature compressive sampling SAR imaging. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium, Valencia, Spain, 22–27 July 2018; pp. 5847–5850. [Google Scholar]
- Kim, S.; Koh, K.; Lustig, M.; Boyd, S.; Gorinevsky, D. An interior-point method for large-scale ℓ1-regularized least squares. IEEE J. Sel. Top. Signal Process. 2007, 1, 606–617. [Google Scholar] [CrossRef]
- Nesterov, Y. A method of solving a convex programming problem with convergence rate o(1/k2). Sov. Math. Dokl. 1983, 27, 372–376. [Google Scholar]
- Donoho, D.L.; Maleki, A.; Montanari, A. Message-passing algorithms for compressed sensing. Proc. Nalt. Acad. Sci. USA 2009, 106, 18914–18919. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Beck, A.; Teboulle, M. A fast iterative shrinkage-thresholding algorithm for linear inverse problems. SIAM J. Imaging Sci. 2009, 2, 183–202. [Google Scholar] [CrossRef]
- Becker, S.R.; Candès, E.J.; Grant, M.C. Templates for convex cone problems with applications to sparse signal recovery. Math. Program. Comput. 2011, 3, 165. [Google Scholar] [CrossRef]
- Bhattacharya, S.; Blumensath, T.; Mulgrew, B.; Davies, M. Fast encoding of synthetic aperture radar raw data using compressed sensing. In Proceedings of the IEEE/SP 14th Workshop on Statistical Signal Processing, Madison, WI, USA, 26–29 August 2007; pp. 448–452. [Google Scholar]
- Alonso, M.T.; Lopez-Dekker, P.; Mallorqui, J.J. A novel strategy for radar imaging based on compressive sensing. IEEE Trans. Geosci. Remote Sens. 2010, 48, 4285–4295. [Google Scholar] [CrossRef]
- Chen, S.; Xi, F. Quadrature compressive sampling for multiband radar echo signals. IEEE Access. 2017, 5, 19742–19760. [Google Scholar] [CrossRef]
- Michael, N.; Shah, S.; Das, J.; Sandeep, M.M.; Vijaykumar, C. Non uniform digitizer for alias-free sampling of wideband analog signals. In Proceedings of the In TENCON 2007—2007 IEEE Region 10 Conference, Taipei, Taiwan, 30 October–2 November 2007; pp. 1–4. [Google Scholar]
- Baraniuk, R.; Davenport, M.; Duarte, M.; Hegde, C. An Introduction to Compressive Sensing; Connexions e-Textbook. 2011. Available online: http://cnx.org/content/col11133/1.5 (accessed on 14 May 2015).
- Beck, A.; Teboulle, M. Guide to the Matlab Code for Wavelet-Based Deblurring with FISTA. Available online: http://iew3.technion.ac.il/~becka/papers/wavelet_FISTA.zip (accessed on 19 June 2018).
- Wright, S.J.; Nowak, R.D.; Figueiredo, M.A.T. Sparse reconstruction by separable approximation. IEEE Trans. Signal Process. 2009, 57, 2479–2493. [Google Scholar] [CrossRef]
- Fang, J.; Xu, Z.; Zhang, B.; Hong, W.; Wu, Y. Fast compressed sensing SAR imaging based on approximated observation. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 352–363. [Google Scholar] [CrossRef]
- Cumming, I.G.; Wong, F.H. Digital Signal Processing of Synthetic Aperture Radar Data: Algorithms and Implementation; Artech House: Norwood, MA, USA, 2004. [Google Scholar]
- Ledoux, M. The Concentration of Measure Phenomenon; American Mathematical Society: Washington, DC, USA, 2001. [Google Scholar]
- Sanandaji, B.M.; Vincent, T.L.; Wakin, M.B. Concentration of measure inequalities for Toeplitz matrices with applications. IEEE Trans. Signal Process. 2013, 61, 109–117. [Google Scholar] [CrossRef]
- Foucart, S.; Rauhut, H. A Mathematical Introduction to Compressive Sensing; Springer: New York, USA, 2013. [Google Scholar]
- Figueiredo, M.A.T.; Nowak, R.D.; Wright, S.J. Gradient projection for sparse reconstruction: Application to compressed sensing and other inverse problems. IEEE J. Sel. Top. Signal Process. 2007, 1, 586–597. [Google Scholar] [CrossRef]
- Rockafellar, R.T. Convex Analysis; Princeton University Press: Princeton, NJ, USA, 1970. [Google Scholar]
- Khwaja, A.S.; Ferro-Famil, L.; Pottier, E. Efficient SAR raw data generation for anisotropic urban scenes based on inverse processing. IEEE Geosci. Remote Sens. Lett. 2009, 6, 757–761. [Google Scholar] [CrossRef]
- Qiu, X.; Hu, D.; Zhou, L.; Ding, C. A bistatic SAR raw data simulator based on inverse ω-k algorithm. IEEE Trans. Geosci. Remote Sens. 2010, 48, 1540–1547. [Google Scholar]
- Deledalle, C. Probabilistic Patch-Based Filter (ppb). Available online: http://www.ceremade.dauphine.fr/~deledall/ppb.php (accessed on 16 June 2018).
- Tao, T. Topics in Random Matrix Theory; American Mathematical Society: Washington, DC, USA, 2012. [Google Scholar]
- Massart, P. About the constants in Talagrand’s concentration inequalities for empirical processes. Ann. Probab. 2000, 28, 863–884. [Google Scholar] [CrossRef]
- Candès, E.J. The restricted isometry property and its implications for compressed sensing. C. R. Math. 2008, 346, 589–592. [Google Scholar] [CrossRef]









| Parameter | Value |
|---|---|
| Carrier frequency | 5.3 GHz |
| Fast-time frequency bandwidth | 30.11 MHz |
| Pulse width | 41.74 s |
| Pulse repetition frequency | 1256.98 Hz |
| Effective radar velocity | 7062 m/s |
| Slant range of scene center | 150.1 km |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, H.; Chen, C.; Chen, S.; Xi, F. Sub-Nyquist SAR via Quadrature Compressive Sampling with Independent Measurements. Remote Sens. 2019, 11, 472. https://doi.org/10.3390/rs11040472
Yang H, Chen C, Chen S, Xi F. Sub-Nyquist SAR via Quadrature Compressive Sampling with Independent Measurements. Remote Sensing. 2019; 11(4):472. https://doi.org/10.3390/rs11040472
Chicago/Turabian StyleYang, Huizhang, Chengzhi Chen, Shengyao Chen, and Feng Xi. 2019. "Sub-Nyquist SAR via Quadrature Compressive Sampling with Independent Measurements" Remote Sensing 11, no. 4: 472. https://doi.org/10.3390/rs11040472