An Adaptive Denoising and Detection Approach for Underwater Sonar Image
Abstract
:1. Introduction
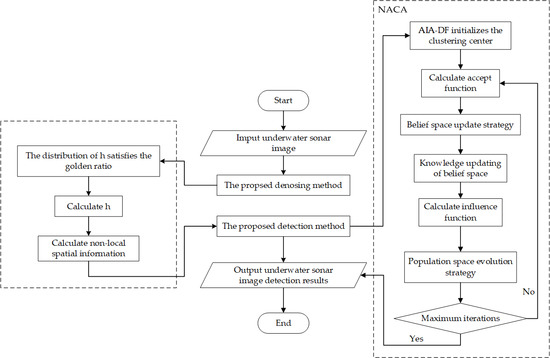
2. Non-Local Spatial Information Denoising Method
2.1. Non-Local Spatial Information
2.2. Our Proposed Denoising Method—An Adaptive Non-Local Spatial Information Denoising Algorithm Based on the Golden Ratio
| Algorithm 1: the proposed denoising method |
| Input: Original sonar image; |
| Output: Denoising image; |
| Initialization: (the radius of search window), (the radius of neighbourhood window); |
| Procedure: |
| 1: For to do: |
| 2: Calculate using Equation (6); |
| 3: Calculate using Equation (5); |
| 4: For every search window in the input image, do: |
| 5: For any two different neighbourhood windows in the search window, do: |
| 6: Calculate the weighted Euclidean distance using Equation (4); |
| 7: Calculate the filtering degree parameter using Equation (9); |
| 8: Calculate and when the result of Equation (8) satisfies the golden ratio; |
| 9: For every search window in the input image, do: |
| 10: Calculate the filtering degree parameter using Equation (8); |
| 11: Calculate using Equation (3); |
| 12: Calculate using Equation (2); |
| 13: Calculate non-local spatial information using Equation (1). |
3. Culture Algorithm
3.1. Cultural Algorithm Framework
3.2. Our Proposed Cultural Algorithm—A New Adaptive Culture Algorithm
3.2.1. Adaptive Initialization Algorithm Based on Data Field
| Algorithm 2: the proposed AIA-DF |
| Input: Denoising image; |
| Output: Initialized image; |
| Initialization: (the radius of the neighbourhood window), (the number of the optimal threshold), (the set of optimal threshold potential solutions); |
| Procedure: |
| 1: For every pixel in the input image, do: |
| 2: Calculate the mean grey of its neighbourhood; |
| 3: Establish the two-dimensional grey histogram of the input image; |
| 4: Establish the data field according to the grey histogram; |
| 5: repeat: |
| 6: Calculate the entropy of using Equation (15); |
| 7: Calculate the entropy of using Equation (16); |
| 8: Calculate the optimal threshold when the maximum of Equation (17) is obtained; |
| 9: Calculate using Equation (19); |
| 10: Update using Equation (18): |
| 11: Update using : |
| 12: Until: the stopping criteria are met. |
3.2.2. New Update Strategy
4. Experiments and Discussion
4.1. The Characteristics of the Underwater Sonar Images
4.2. The Effectiveness Verification of the Proposed Denoising Method
4.3. The Effectiveness Demonstration of the Proposed Detection Method
4.4. The Performance Analysis of the New Update Strategy in NACA
4.5. The Adaptability Demonstration of the Proposed Denoising Method and Detection Method
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Wang, X.; Guo, L.; Yin, J.; Liu, Z.; Han, X. Narrowband Chan-Vese model of sonar image segmentation: An adaptive ladder initialization approach. Appl. Acoust. 2016, 113, 238–254. [Google Scholar] [CrossRef]
- Ye, X.; Zhang, Z.; Liu, P.; Guan, H. Sonar image segmentation based on GMRF and Level-set models. Ocean Eng. 2010, 37, 891–901. [Google Scholar] [CrossRef]
- Wang, X.; Liu, S.; Teng, X.; Sun, J.; Jiao, J. SFLA with PSO local search for detection sonar image. In Proceedings of the 2016 35th Chinese Control Conference, Chengdu, China, 27–29 July 2016; pp. 3852–3857. [Google Scholar]
- Wu, J.P.; Guo, H. A method for sonar image segmentation based on combination of MRF and region growing. In Proceedings of the 2015 5th International Conference on Communication Systems and Network Technologies, Gwalior, India, 4–6 April 2015; pp. 457–460. [Google Scholar]
- Zhu, Z.; Yin, H.; Chai, Y.; Li, Y.; Qi, G. A novel multi-modality image fusion method based on image decomposition and sparse representation. Inf. Sci. 2018, 432, 516–529. [Google Scholar] [CrossRef]
- Li, H.; Qiu, H.; Yu, Z.; Li, B. Multifocus image fusion via fixed window technique of multiscale images and non-local means filtering. Signal Process. 2017, 138, 71–85. [Google Scholar] [CrossRef]
- Wang, X.; Liu, S.; Liu, Z. Underwater sonar image detection: A combination of non-local spatial information and quantum-inspired shuffled frog leaping algorithm. PLoS ONE 2017, 12, e0177666. [Google Scholar] [CrossRef]
- Zhao, F.; Jiao, L.; Liu, H.; Gao, X. A novel fuzzy clustering algorithm with non-local adaptive spatial constraint for image segmentation. Signal Process. 2011, 91, 988–999. [Google Scholar] [CrossRef]
- Zhao, F. Fuzzy clustering algorithms with self-tuning non-local spatial information for image segmentation. Neurocomputing 2013, 106, 115–125. [Google Scholar] [CrossRef]
- Wang, L. Segmentation algorithm of fuzzy clustering on side scan sonar image. J. Huazhong Univ. Sci. Technol. 2012, 40, 25–29. [Google Scholar]
- Mignotte, M.; Collect, C.; Perez, P.; Bouthemy, P. Three-class markovian segmentation of high-resolution sonar image. Comput. Vis. Image Underst. 1999, 76, 191–204. [Google Scholar] [CrossRef]
- Mignotte, M.; Collect, C.; Perez, P.; Bouthemy, P. Sonar image segmentation using an unsupervised hierarchical MRF model. IEEE Trans. Signal Process. 2000, 9, 1216–1231. [Google Scholar] [CrossRef]
- Vese, L.; Chan, T. A multiphase level set framework for image segmentation using the mumford and shah model. Int. J. Comput. Vis. 2002, 50, 271–293. [Google Scholar] [CrossRef]
- Lianantonakis, M.; Petillot, Y. Sidescan sonar segmentation using active contours and level set methods. In Proceedings of the Oceans Europe 2005, Brest, France, France, 20–23 June 2005; pp. 719–724. [Google Scholar]
- Lianantonakis, M.; Petillot, Y. Sidescan sonar segmentation using texture descriptors and active contours. IEEE J. Ocean. Eng. 2007, 32, 744–752. [Google Scholar] [CrossRef]
- Liu, G.; Bian, H.; Shi, H. Sonar image segmentation based on an improved level set method. Phys. Procedia 2012, 33, 1168–1175. [Google Scholar] [CrossRef]
- Awad, N.; Ali, M.; Suganthan, P.; Reynolds, R. CADE: A Hybridization of cultural algorithm and differential evolution for numerical optimization. Inf. Sci. 2017, 378, 215–241. [Google Scholar] [CrossRef]
- Khatami, A.; Mirghasemi, S.; Khosravi, A.; Lim, C.P.; Nahavandi, S. A new PSO-based approach to fire flame detection using K-Medoids clustering. Expert Syst. Appl. 2017, 68, 69–80. [Google Scholar] [CrossRef]
- Morra, L.; Coccia, N.; Cerquitelli, T. Optimization of computer aided detection systems: An evolutionary approach. Expert Syst. Appl. 2018, 100, 45–156. [Google Scholar] [CrossRef]
- Wei, Z.; Bu, Y. Cultural particle swarm optimization algorithm and its application. In Proceedings of the 2012 24th Chinese Control and Decision Conference, Taiyuan, China, 23–25 May 2012; pp. 740–744. [Google Scholar]
- Liu, T.; Jiao, L.; Ma, W.; Ma, J.; Shang, R. A new quantum-behaved particle swarm optimization based on cultural evolution mechanism for multiobjective problems. Knowl. Based Syst. 2016, 101, 90–99. [Google Scholar] [CrossRef]
- Wang, X.; Hao, W.; Li, Q. An adaptive cultural algorithm with improved quantum-behaved particle swarm optimization for sonar image detection. Sci. Rep. 2017, 7, 17733. [Google Scholar] [CrossRef]
- Wang, S.; Wang, D.; Li, C.; Li, Y.; Ding, G. Clustering by fast search and find of density peaks with data field. Chin. J. Electron. 2016, 25, 397–402. [Google Scholar] [CrossRef]
- Zhang, Y.; Lu, K.; Gao, Y. Quantum algorithms and quantum-inspired algorithms. Chin. J. Comput. 2013, 36, 1835–1842. [Google Scholar] [CrossRef]
- Wang, X.; Liu, S.; Li, Q.; Liu, Z. Underwater sonar image detection: A novel quantum-inspired shuffled frog leaping algorithm. Chin. J. Electron. 2018, 27, 588–594. [Google Scholar] [CrossRef]
- Ding, W.; Wang, J.; Guan, Z.; Shi, Q. Enhanced minimum attribute reduction based on quantum-inspired shuffled frog leaping algorithm. J. Syst. Eng. Electron. 2013, 24, 426–434. [Google Scholar] [CrossRef]
- Ding, W.; Wang, J.; Guan, Z. A minimum attribute self-adaptive cooperative co-evolutionary reduction algorithm based on quantum elitist frogs. J. Comput. Res. Dev. 2014, 51, 743–753. [Google Scholar]
- Zhang, B.; Qi, H.; Sun, S.; Ruan, L.; Tan, H. Solving inverse problems of radiative heat transfer and phase change in semitransparent medium by using improved quantum particle swarm optimization. Int. J. Heat Mass Transf. 2015, 85, 300–310. [Google Scholar] [CrossRef]




















| - | |||
|---|---|---|---|
| 1 | 0.030 | 0.050 | 0.539 |
| 2 | 0.040 | 0.200 | 0.609 |
| 3 | 0.015 | 0.030 | 0.689 |
| 4 | 0.020 | 0.035 | 0.624 |
| 5 | 0.010 | 0.050 | 0.634 |
| 6 | 0.010 | 0.040 | 0.584 |
| 7 | 0.005 | 0.040 | 0.617 |
| 8 | 0.010 | 0.035 | 0.681 |
| 9 | 0.005 | 0.030 | 0.532 |
| 10 | 0.010 | 0.040 | 0.575 |
| 11 | 0.002 | 0.005 | 0.567 |
| 12 | 0.030 | 0.100 | 0.604 |
| 13 | 0.005 | 0.040 | 0.676 |
| 14 | 0.010 | 0.060 | 0.636 |
| 15 | 0.005 | 0.015 | 0.650 |
| 16 | 0.005 | 0.020 | 0.649 |
| 17 | 0.010 | 0.025 | 0.605 |
| 18 | 0.020 | 0.035 | 0.571 |
| 19 | 0.005 | 0.070 | 0.556 |
| 20 | 0.030 | 0.050 | 0.539 |
| Iterative Times | NACA | QSFLA-NSM | ACA-IQPSO | QSFLA | CPSO | QPSO |
|---|---|---|---|---|---|---|
| 1 | 3.024 | 2.188 | 2.028 | 1.969 | 1.737 | 1.724 |
| 2 | 3.024 | 2.495 | 2.320 | 2.554 | 2.100 | 2.024 |
| 3 | 3.024 | 2.695 | 2.520 | 2.554 | 2.236 | 2.083 |
| 4 | 3.024 | 2.695 | 2.520 | 2.554 | 2.315 | 2.083 |
| 5 | 3.024 | 2.695 | 2.520 | 2.554 | 2.417 | 2.241 |
| 6 | 3.087 | 2.695 | 2.806 | 2.554 | 2.417 | 2.241 |
| 7 | 3.087 | 2.695 | 2.806 | 2.554 | 2.421 | 2.241 |
| 8 | 3.087 | 2.862 | 2.806 | 2.727 | 2.475 | 2.410 |
| 9 | 3.087 | 2.862 | 2.806 | 2.727 | 2.475 | 2.410 |
| 10 | 3.087 | 2.862 | 2.806 | 2.727 | 2.475 | 2.410 |
| Iterative Times | NACA | QSFLA-NSM | ACA-IQPSO | QSFLA | CPSO | QPSO |
|---|---|---|---|---|---|---|
| 1 | 2.365 | 2.184 | 2.003 | 1.956 | 1.794 | 2.066 |
| 2 | 2.477 | 2.184 | 2.003 | 2.080 | 1.951 | 2.066 |
| 3 | 2.477 | 2.212 | 2.003 | 2.080 | 2.103 | 2.170 |
| 4 | 2.477 | 2.212 | 2.133 | 2.312 | 2.103 | 2.170 |
| 5 | 2.532 | 2.212 | 2.133 | 2.337 | 2.162 | 2.170 |
| 6 | 2.532 | 2.426 | 2.133 | 2.337 | 2.226 | 2.170 |
| 7 | 2.532 | 2.426 | 2.273 | 2.337 | 2.226 | 2.184 |
| 8 | 2.532 | 2.426 | 2.273 | 2.337 | 2.253 | 2.209 |
| 9 | 2.532 | 2.426 | 2.273 | 2.337 | 2.253 | 2.209 |
| 10 | 2.532 | 2.426 | 2.273 | 2.337 | 2.253 | 2.209 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, X.; Li, Q.; Yin, J.; Han, X.; Hao, W. An Adaptive Denoising and Detection Approach for Underwater Sonar Image. Remote Sens. 2019, 11, 396. https://doi.org/10.3390/rs11040396
Wang X, Li Q, Yin J, Han X, Hao W. An Adaptive Denoising and Detection Approach for Underwater Sonar Image. Remote Sensing. 2019; 11(4):396. https://doi.org/10.3390/rs11040396
Chicago/Turabian StyleWang, Xingmei, Qiming Li, Jingwei Yin, Xiao Han, and Wenqian Hao. 2019. "An Adaptive Denoising and Detection Approach for Underwater Sonar Image" Remote Sensing 11, no. 4: 396. https://doi.org/10.3390/rs11040396