Establishment of a Real-Time Local Tropospheric Fusion Model
Abstract
:1. Introduction
2. Materials and Methods
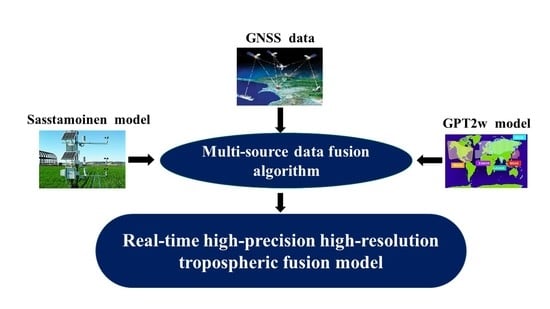
2.1. Multisource Tropospheric Data
2.1.1. Zenith Tropospheric Delay Obtained by GNSS Processing
2.1.2. Zenith Tropospheric Delay Obtained by the Saastamoinen Model
2.1.3. Zenith Tropospheric Delay Obtained by the GPT2w Model
2.2. Methods for Establishing the Local Tropospheric Fusion Model
2.2.1. Tropospheric Fusion Modeling
2.2.2. Precise Weights Determination
- The prior weights of the different observed values, i.e., the initial values of the weight of each type of observation (P1, P2, …), are assigned.
- A first adjustment is made, to obtain the values of .
- In accordance with Equations (10) or (11) for the first-time variance component estimation, the first value of the unit weight variance of various observations is obtained, and then the weights are determined according to the following formula:where c is a constant. Generally, one of the values is selected.
2.3. Data Description and Processing Strategy
3. Results and Discussion
3.1. Verification of the Systematic Bias Estimation
3.2. Verification of the Zenith Tropospheric Delay
3.2.1. Active Troposphere Condition
3.2.2. Quiet Troposphere Condition
3.3. Impact of the dDstribution of Modeling Station Elevations on Model Precision
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Yao, Y.; Xu, X.; Xu, C.; Peng, W.; Wan, Y. GGOS tropospheric delay forecast product performance evaluation and its application in real-time PPP. J. Atmos. Sol.-Terr. Phys. 2018, 175, 1–17. [Google Scholar] [CrossRef]
- Kim, J.; Song, J.; No, H.; Han, D.; Kim, D.; Park, B.; Kee, C. Accuracy Improvement of DGPS for Low-Cost Single-Frequency Receiver Using Modified Flächen Korrektur Parameter Correction. ISPRS Int. J. Geo-Inf. 2017, 6, 222. [Google Scholar] [CrossRef]
- Ahn, Y.W.; Kim, D.; Dare, P. Local tropospheric anomaly effects on GPS RTK performance. Proc. ION GNSS 2006, 2006, 1925–1935. [Google Scholar]
- Song, J.; Park, B.; Kee, C. Comparative Analysis of Height-Related Multiple Correction Interpolation Methods with Constraints for Network RTK in Mountainous Areas. J. Navig. 2016, 69, 991–1010. [Google Scholar] [CrossRef] [Green Version]
- Collins, J.P.; Langley, R. The residual tropospheric propagation delay: How bad can it get? In Proceedings of Ion gps. Inst. Navig. 1998, 11, 729–738. [Google Scholar]
- Collins, J.P.; Langley, R.B. A Tropospheric Delay Model for the User of the Wide Area Augmentation System; Department of Geodesy and Geomatics Engineering, University of New Brunswick: Fredericton, NB, USA, 1997. [Google Scholar]
- MOPS, W. Minimum Operational Performance Standards for Global Positioning System/Wide Area Augmentation System Airborne Equipment; RTCA Inc.: Washington, DC, USA, 1999; Documentation No. RTCA/DO-229B, 6. [Google Scholar]
- Penna, N.; Dodson, A.; Chen, W. Assessment of EGNOS Tropospheric Correction Model. J. Navig. 2001, 54, 37–55. [Google Scholar] [CrossRef] [Green Version]
- Ueno, M.; Hoshinoo, K.; Matsunaga, K.; Kawai, M.; Nakao, H.; Langley, R.B.; Bisnath, S.B. Assessment of atmospheric delay correction models for the Japanese MSAS. In Proceedings of the 14th International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GPS 2001), Salt Lake City, UT, USA, 11–14 September 2001; pp. 2341–2350. [Google Scholar]
- Boehm, J.; Heinkelmann, R.; Schuh, H.; Böhm, J. Short Note: A global model of pressure and temperature for geodetic applications. J. Geod. 2007, 81, 679–683. [Google Scholar] [CrossRef]
- Kouba, J. Testing of global pressure/temperature (GPT) model and global mapping function (GMF) in GPS analyses. J. Geod. 2009, 83, 199–208. [Google Scholar] [CrossRef]
- Petit, G.; Luzum, B. IERS conventions 2010, IERS Technical Note; IERS Conventions Centre: Paris, France, 2010. [Google Scholar]
- Lu, C.; Zus, F.; Ge, M.; Heinkelmann, R.; Dick, G.; Wickert, J.; Schuh, H. Tropospheric delay parameters from numerical weather models for multi-GNSS precise positioning. Atmos. Meas. Techn. 2016, 9, 5965–5973. [Google Scholar] [CrossRef] [Green Version]
- Lagler, K.; Schindelegger, M.; Böhm, J.; Krásná, H.; Nilsson, T. GPT2: Empirical slant delay model for radio space geodetic techniques. Geophys. Lett. 2013, 40, 1069–1073. [Google Scholar] [CrossRef] [Green Version]
- Böhm, J.; Möller, G.; Schindelegger, M.; Pain, G.; Weber, R. Development of an improved empirical model for slant delays in the troposphere (GPT2w). GPS Solut. 2014, 19, 433–441. [Google Scholar] [CrossRef] [Green Version]
- Hopfield, H.S. Two-quartic Tropospheric Refractivity Profile for Correcting Satellite Data. J. Geophys. Res. 1969, 74, 4487–4499. [Google Scholar] [CrossRef]
- Saastamoinen, J. Atmospheric Correction for Troposphere and Stratosphere in Radio Ranging of Satellites. Use Artif. Satell. Geod. 1972, 15, 247–251. [Google Scholar]
- Black, H.D. An easily implemented algorithm for the tropospheric range correction. J. Geophy. Res. Solid Earth 1978, 83, 1825–1828. [Google Scholar] [CrossRef]
- Qu, W.; Zhu, W.; Song, S.; Ping, J. Three kinds of tropospheric delay correction model accuracy evaluation. J. Astron. 2008, 49, 113–122. [Google Scholar]
- Tao, W. Near real-time GPS PPP-inferred water vapor system development and evaluation. Master’s Thesis, Department of Geomatics Engineering, University of Calgary, Calgary, AB, Canada, 2008. [Google Scholar]
- Ye, S.; Zhang, S.; Liu, J. Precision single point positioning method is used to estimate the accuracy of tropospheric delay. J. Wuhan Univ. (Inf. Sci. Ed.) 2008, 33, 788–791. [Google Scholar]
- Wang, M.; Chai, H.; Xie, K.; Chen, Y. PWV inversion based on CNES realtime orbits and clocks. J. Geod. Geodyn. 2013, 33, 137–140. [Google Scholar]
- Shi, J.; Xu, C.; Guo, J.; Gao, Y. Local troposphere augmentation for real-time precise point positioning. Earth Planets Space 2014, 66, 1–13. [Google Scholar] [CrossRef]
- Douša, J.; Václavovic, P.; Zhao, L.; Kačmařík, M. New adaptable all-in-one strategy for estimating advanced tropospheric parameters and using real-time orbits and clocks. Remote Sens. 2018, 10, 232. [Google Scholar] [CrossRef]
- Douša, J.; Eliaš, M.; Václavovic, P.; Eben, K.; Krč, P. A two-stage tropospheric correction model combining data from GNSS and numerical weather model. GPS Solut. 2018, 22, 77. [Google Scholar] [CrossRef]
- Rocken, C.; Ware, R.; Hove, T.V.; Solheim, F.; Alber, C.; Johnson, J.; Bevis, M.; Businger, S. Sensing atmospheric water vapor with the global positioning system. Geophys. Res. Lett. 2013, 20, 2631–2634. [Google Scholar] [CrossRef]
- Ifadis, I.I. The Atmospheric Delay of Radio Waves: Modeling the Elevation Dependence on a Global Scale; Technical Report No. 38L; Chalmers, U. of Technology: Goteburg, Sweden, 1986. [Google Scholar]
- Askne, J.; Nordius, H. Estimation of Tropospheric Delay for Mircowaves from Surface Weather Data. Radio Sci. 1987, 22, 379–386. [Google Scholar] [CrossRef]
- Thayer, G.D. An improved equation for the radio refractive index of air. Radio Sci. 1974, 9, 803–807. [Google Scholar] [CrossRef]
- Teunissen, P.J.G.; Amiri-Simkooei, A.R. Least-squares variance component estimation. J. Geod. 2008, 82, 65–82. [Google Scholar] [CrossRef]
- Grafarend, E.; Kleusberg, A.; Schaffrin, B. An introduction to the variance-covariance component estimation of Helmert type. Zeitschrift für Vermessungswesen 1980, 105, 161–180. [Google Scholar]
- Cui, X.Z.; Yu, Z.C.; Tao, B.Z.; Liu, D.J. Generalized Surveying Adjustment (New Edition); Wuhan University Press: Wuhan, China, 2005. [Google Scholar]
- Chen, Q.; Song, S.; Heise, S.; Liou, Y.; Zhu, W.; Zhao, J. Assessment of ZTD derived from ECMWF/NCEP data with GPS ZTD over China. GPS Solut. 2011, 15, 415–425. [Google Scholar] [CrossRef]
- Hua, Z.; Liu, L.; Liang, X. An Assessment of GPT2w Model and Fusion of a Troposphere Model with in Situ Data; Geomatics & Information Science of Wuhan University: Wuhan, China, 2017. [Google Scholar]
- Kouba, J.; Héroux, P. Precise Point Positioning Using IGS Orbit and Clock Products. GPS Solut. 2001, 5, 12–28. [Google Scholar] [CrossRef]









| Data source | Period | CORS Station | Weather Station | GPT2w |
|---|---|---|---|---|
| Grid Points | ||||
| Hong Kong | 20 July 2015~26 July 2015 1 August 2015~7 August 2015 | 15 | 14 | 4 (1°×1°) 21.5°~22.5° 113.5°~114.5° |
| DOY | Helmert | Comprehensive | ||
|---|---|---|---|---|
| Bias (cm) | RMS (cm) | Bias (cm) | RMS (cm) | |
| 201.00 | 0.00 | 1.33 | 0.04 | 1.28 |
| 202.00 | 0.35 | 1.84 | 0.22 | 1.73 |
| 203.00 | −0.40 | 1.10 | −0.28 | 1.13 |
| 204.00 | −0.23 | 1.05 | −0.06 | 1.05 |
| 205.00 | −0.06 | 1.58 | 0.22 | 1.59 |
| 206.00 | 0.58 | 1.98 | 0.53 | 1.93 |
| 207.00 | 0.82 | 2.02 | 0.70 | 1.55 |
| 213.00 | 0.97 | 2.86 | 0.60 | 2.19 |
| 214.00 | 0.55 | 1.82 | 0.50 | 1.53 |
| 215.00 | −0.11 | 1.31 | 0.13 | 1.21 |
| 216.00 | −0.28 | 1.30 | 0.15 | 1.30 |
| 217.00 | -0.62 | 1.97 | -0.16 | 1.41 |
| 218.00 | -0.23 | 1.40 | -0.06 | 1.10 |
| 219.00 | -0.12 | 2.71 | -0.18 | 1.38 |
| Mean | 0.0871 | 1.7336 | 0.1679 | 1.4557 |
| DOY | Fusion-Model | PPP-Model | GPT2w | SAAS | ||||
|---|---|---|---|---|---|---|---|---|
| bias | RMS | bias | RMS | bias | RMS | bias | RMS | |
| 201 | 0.04 | 1.28 | −0.19 | 1.43 | −8.59 | 8.66 | −13.02 | 13.10 |
| 202 | 0.27 | 1.82 | −0.44 | 1.43 | −6.55 | 6.59 | −11.08 | 11.22 |
| 203 | −0.29 | 1.15 | 0.14 | 0.81 | −7.12 | 7.17 | −8.90 | 9.04 |
| 204 | −0.06 | 1.04 | 0.20 | 0.89 | −6.52 | 6.57 | −8.67 | 8.78 |
| 205 | 0.22 | 1.60 | −0.93 | 2.03 | −3.99 | 4.11 | −6.10 | 6.41 |
| 206 | 0.52 | 1.91 | −0.55 | 2.01 | −1.83 | 2.27 | −4.75 | 5.11 |
| 207 | 0.70 | 1.56 | −0.05 | 1.51 | −0.01 | 1.03 | −2.37 | 2.90 |
| mean | 0.20 | 1.48 | −0.26 | 1.44 | −4.94 | 5.20 | −7.84 | 8.08 |
| DOY | Fusion-Model | PPP-Model | GPT2w | SAAS | ||||
|---|---|---|---|---|---|---|---|---|
| bias | RMS | bias | RMS | bias | RMS | bias | RMS | |
| 213 | 0.61 | 2.20 | −0.26 | 2.01 | 7.37 | 7.47 | 2.79 | 4.44 |
| 214 | 0.49 | 1.49 | −0.56 | 1.49 | 9.72 | 9.75 | 5.68 | 5.88 |
| 215 | 0.14 | 1.20 | −0.15 | 1.03 | 10.15 | 10.18 | 6.34 | 6.57 |
| 216 | 0.16 | 1.32 | 0.15 | 1.15 | 8.07 | 8.11 | 2.64 | 3.27 |
| 217 | −0.16 | 1.41 | 0.24 | 1.12 | 7.75 | 7.87 | 2.98 | 3.87 |
| 218 | −0.04 | 1.08 | −0.09 | 0.90 | 7.09 | 7.16 | 2.04 | 3.49 |
| 219 | −0.24 | 1.42 | −0.16 | 0.86 | 6.34 | 6.40 | 0.08 | 4.87 |
| mean | 0.14 | 1.45 | −0.12 | 1.22 | 8.07 | 8.13 | 3.22 | 4.63 |
| DOY | Site Involved in Modeling | HKNP | HKST | ||||||
|---|---|---|---|---|---|---|---|---|---|
| bias | RMS | bias | RMS | ||||||
| 201 | HKKS(44.69 m) | HKKT(34.54 m) | HKLM(8.53 m) | HKLT(125.90 m) | HKMW(194.94 m) | 2.10 | 2.75 | 1.29 | 1.64 |
| 202 | HKKS(44.69 m) | HKKT(34.54 m) | HKLM(8.53 m) | HKLT(125.89 m) | HKMW(194.94 m) | 3.91 | 4.68 | 2.34 | 2.75 |
| 203 | HKKS(44.69 m) | HKKT(34.54 m) | HKLT(125.89 m) | HKMW(194.94 m) | HKNP(350.67 m) | 0.27 | 0.37 | 0.85 | 1.43 |
| 204 | HKKS(44.69 m) | HKKT(34.54 m) | HKLM(8.53 m) | HKLT(125.89 m) | HKNP(350.67 m) | 0.41 | 0.44 | 1.44 | 2.11 |
| 205 | HKKS(44.69 m) | HKKT(34.54 m) | HKLM(8.53 m) | HKLT(125.89 m) | HKMW(194.94 m) | 2.83 | 3.04 | 2.17 | 2.40 |
| 206 | HKKS(44.69 m) | HKKT(34.54 m) | HKLM(8.53 m) | HKLT(125.89 m) | HKMW(194.94 m) | 3.91 | 4.71 | 2.60 | 2.90 |
| 207 | HKKS(44.69 m) | HKKT(34.54 m) | HKLM(8.53 m) | HKLT(125.89 m) | HKMW(194.94 m) | 1.89 | 3.44 | 2.60 | 2.82 |
| 213 | HKKS(44.69 m) | HKKT(34.54 m) | HKLM(8.53 m) | HKLT(125.89 m) | HKMW(194.94 m) | 3.74 | 5.61 | 3.26 | 3.49 |
| 214 | HKKS(44.69 m) | HKKT(34.54 m) | HKLM(8.53 m) | HKLT(125.89 m) | HKMW(194.94 m) | 3.36 | 3.94 | 2.44 | 2.73 |
| 215 | HKKS(44.69 m) | HKKT(34.54 m) | HKLM(8.53 m) | HKLT(125.89 m) | HKNP(350.67 m) | 0.03 | 0.04 | 2.20 | 2.73 |
| 216 | HKKS(44.69 m) | HKKT(34.54 m) | HKLM(8.53 m) | HKLT(125.89 m) | HKNP(350.67 m) | 0.04 | 0.06 | 2.09 | 2.69 |
| 217 | HKKS(44.69 m) | HKKT(34.54 m) | HKLM(8.53 m) | HKLT(125.89 m) | HKNP(350.67 m) | 0.01 | 0.04 | 1.23 | 2.47 |
| 218 | HKKS(44.69 m) | HKKT(34.54 m) | HKLM(8.53 m) | HKLT(125.89 m) | HKNP(350.67 m) | 0.00 | 0.03 | 1.21 | 1.96 |
| 219 | HKKS(44.69 m) | HKKT(34.54 m) | HKLM(8.53 m) | HKLT(125.89 m) | HKNP(350.67 m) | 0.01 | 0.02 | -1.43 | 2.95 |
| Station | Height (m) | DOY203 | |
|---|---|---|---|
| bias | RMS | ||
| HKKS | 44.692 | 0.13 | 0.40 |
| HKKT | 34.538 | −0.59 | 0.73 |
| HKLT | 125.89 | 0.02 | 0.42 |
| HKMW | 194.936 | 0.17 | 0.29 |
| HKNP | 350.666 | 0.27 | 0.37 |
| HKOH | 166.375 | 0.69 | 1.48 |
| HKPC | 18.083 | −1.03 | 1.50 |
| HKSC | 20.204 | −0.56 | 1.17 |
| HKSL | 95.266 | 0.42 | 0.56 |
| HKSS | 38.684 | −0.66 | 0.89 |
| HKST | 258.687 | 0.85 | 1.43 |
| HKTK | 22.497 | −1.09 | 1.35 |
| HKWS | 63.762 | −0.08 | 0.52 |
| T430 | 41.29 | -1.10 | 1.20 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yao, Y.; Xu, X.; Xu, C.; Peng, W.; Wan, Y. Establishment of a Real-Time Local Tropospheric Fusion Model. Remote Sens. 2019, 11, 1321. https://doi.org/10.3390/rs11111321
Yao Y, Xu X, Xu C, Peng W, Wan Y. Establishment of a Real-Time Local Tropospheric Fusion Model. Remote Sensing. 2019; 11(11):1321. https://doi.org/10.3390/rs11111321
Chicago/Turabian StyleYao, Yibin, Xingyu Xu, Chaoqian Xu, Wenjie Peng, and Yangyang Wan. 2019. "Establishment of a Real-Time Local Tropospheric Fusion Model" Remote Sensing 11, no. 11: 1321. https://doi.org/10.3390/rs11111321