Introduction of the Double-Differenced Ambiguity Resolution into Precise Point Positioning
Abstract
:1. Introduction
2. Mathematical Models
2.1. DD AR
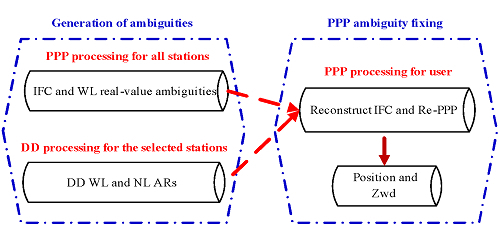
2.2. PPP AR and Positioning
3. Data and Experiments
4. Discussion
4.1. PPP Solutions
4.2. Application in Displacement Monitoring of the Reference Station
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| AR | Ambiguity resolution |
| DCB | Differential code bias |
| DD | Double-differenced |
| FCB | Fractional cycle bias |
| GNSS | Global navigation satellite system |
| IFC | Ionosphere-free combination |
| NL | Narrow lane |
| PCV | Phase center variation |
| PPP | Precise point positioning |
| RMS | Root mean square |
| WL | Wide lane |
References
- Zumberge, J.F.; Heflin, M.B.; Jefferson, D.C.; Watkins, M.M.; Webb, F.H. Precise point positioning for the efficient and robust analysis of GPS d networks. J. Geophys. Res. 1997, 102, 5005–5017. [Google Scholar] [CrossRef]
- Kouba, J. A possible detection of the 26 December 2004 Great Sumatra Andaman Islands earthquake with solution products of the international GNSS service. Stud. Geophys. Geod. 2005, 49, 463–483. [Google Scholar] [CrossRef]
- Rodrigo, F.; Marcelo, C.; Richard, B. Analyzing GNSS data in precise point positioning software. GPS Solut. 2011, 15, 1–13. [Google Scholar]
- Li, H.; Chen, J.; Wang, J.; Hu, C.; Liu, Z. Network based Real-time Precise Point Positioning. Adv. Space Res. 2010, 46, 1218–1224. [Google Scholar] [CrossRef]
- Li, H.; Wang, J.; Chen, J.; Hu, C.; Wang, H. The realization and analysis of GNSS Network based Real-time Precise Point Positioning. Chin. J. Geophys. 2010, 53, 1302–1307. [Google Scholar]
- Yu, W.; Ding, X.; Chen, W.; Dai, W.; Yi, Z.; Zhang, B. Precise point positioning with mixed use of time-differenced and undifferenced carrier phase from multiple GNSS. J. Geod. 2018. [Google Scholar] [CrossRef]
- Bock, H.; Dach, R.; Jäggi, A.; Beutler, G. High-rate GPS clock corrections from CODE: Support of 1 Hz applications. J. Geod. 2009, 83, 1083–1094. [Google Scholar] [CrossRef]
- Li, H.; Chen, J.; Wang, J.; Wu, B. Satellite- and epoch differenced precise point positioning based on regional augmentation network. Sensors 2012, 12, 7518–7528. [Google Scholar] [CrossRef] [PubMed]
- Fang, R.; Shi, C.; Song, W.; Wang, G.; Liu, J. Determination of earthquake magnitude using GPS displacement waveforms from real-time precise point positioning. Geophys. J. Int. 2014, 196, 461–472. [Google Scholar] [CrossRef]
- Geng, T.; Xie, X.; Fang, R.; Su, X.; Zhao, Q.; Liu, G.; Li, H.; Shi, C.; Liu, J. Real-time capture of seismic waves using high-rate multi-GNSS observations: Application to the 2015 Mw7.8 Nepal earthquake. Geophys. Res. Lett. 2016, 43, 161–167. [Google Scholar] [CrossRef]
- Wubbena, G.; Schmitz, M.; Bagg, A. PPP-RTK: Precise point positioning using state-space representation in RTK networks. In Proceedings of the 18th International Technical Meeting of the Satellite Division of the Institute of Navigation (ION GNSS 2005), Long Beach, CA, USA, 13–16 September 2005; pp. 13–16. [Google Scholar]
- Laurichesse, D.; Mercier, F. Integer ambiguity resolution on undifferenced GPS phase measurements and its application to PPP. In Proceedings of the 20th International Technical Meeting of the Satellite Division of the Institute of Navigation (ION GNSS 2007), Fort Worth, TX, USA, 25–28 September 2007; pp. 839–848. [Google Scholar]
- Collins, P. Isolating and estimating undifferenced GPS integer ambiguities. In Proceedings of the 2008 National Technical Meeting of the Institute of Navigation, San Diego, CA, USA, 28–30 January 2008; pp. 720–732. [Google Scholar]
- Ge, M.; Gendt, G.; Rothacher, M.; Shi, C.; Liu, J. Resolution of GPS carrier-phase ambiguities in precise point positioning (PPP) with daily observations. J. Geod. 2008, 82, 389–399. [Google Scholar] [CrossRef]
- Geng, J.; Meng, X.; Dodson, A.H.; Teferle, F.N. Integer ambiguity resolution in precise point positioning: Method comparison. J. Geod. 2010, 84, 569–581. [Google Scholar] [CrossRef]
- Teunissen, P.J.G.; Odijk, D.; Zhang, B. PPP-RTK: Results of CORS network-based PPP with integer ambiguity resolution. J. Aeronaut. Astronaut. Aviat. 2010, 42, 223–229. [Google Scholar]
- Loyer, S.; Perosanz, F.; Mercier, F.; Capdeville, H.; Marty, J.C. Zero difference GPS ambiguity resolution at CNES-CLS IGS analysis center. J. Geod. 2012, 86, 991–1003. [Google Scholar] [CrossRef]
- Lannes, A.; Prieur, J. Calibration of the clock-phase biases of GNSS networks: The closure-ambiguity approach. J. Geod. 2013, 87, 709–731. [Google Scholar] [CrossRef] [Green Version]
- Zhang, X.; Li, P.; Guo, F. Ambiguity resolution in precise point positioning with hourly data for global single receiver. Adv. Space Res. 2013, 51, 153–161. [Google Scholar] [CrossRef]
- Teunissen, P.J.G.; Khodabandeh, A. An analytical study of PPP-RTK corrections: Precision, correlation and user-impact. J. Geod. 2015, 89, 1109–1132. [Google Scholar]
- Katsigianni, G.; Loyer, S.; Perosanz, F.; Mercier, F.; Zajdel, R.; Sośnica, K. Improving Galileo orbit determination using zero-difference ambiguity fixing in a Multi-GNSS processing. Adv. Space Res. 2018. [Google Scholar] [CrossRef]
- Odijk, D.; Zhang, B.; Khodabandeh, A.; Odolinsk, R.; Teunissen, P.J.G. On the estimability of parameters in undifferenced, uncombined GNSS network and PPP-RTK user models by means of S-system theory. J. Geod. 2016, 90, 15–44. [Google Scholar] [CrossRef]
- Li, X.; Zhang, X.; Ge, M. Regional reference network augmented precise point positioning for instantaneous ambiguity resolution. J. Geod. 2011, 85, 151–158. [Google Scholar] [CrossRef]
- Tang, X.; Roberts, G.; Li, X.; Hancock, C. Real-time kinematic PPP GPS for structure monitoring applied on the Severn Suspension Bridge, UK. Adv. Space Res. 2017, 60, 925–937. [Google Scholar] [CrossRef]
- Paziewski, J.; Sieradzki, R.; Baryla, R. Multi-GNSS high-rate RTK, PPP and novel direct phase observation processing method: Application to precise dynamic displacement detection. Meas. Sci. Technol. 2018, 29, 035002. [Google Scholar] [CrossRef]
- Blewitt, G. Fixed point theorems of GPS carrier phase ambiguity resolution and their application to massive network processing: Ambizap. J. Geophys. Res. 2008, 113, B12410. [Google Scholar] [CrossRef]
- Bertiger, W.; Desai, S.; Haines, B.; Harvey, N.; Moore, A.; Owen, S.; Weiss, J. Single receiver phase ambiguity resolution with GPS data. J. Geod. 2010, 84, 327–337. [Google Scholar] [CrossRef]
- Dong, D.; Bock, Y. Global positioning system network analysis with phase ambiguity resolution applied to crustal deformation studies in California. J. Geophys. Res. 1989, 94, 3949–3966. [Google Scholar] [CrossRef]
- Teunissen, P.J.G. The least-squares ambiguity decorrelation adjustment: A method for fast GPS integer ambiguity estimation. J. Geod. 1995, 70, 65–82. [Google Scholar] [CrossRef]
- Chang, X.; Yang, X.; Zhou, T. MLAMBDA: A modified LAMBDA method for integer least-squares estimation. J. Geod. 2005, 79, 552–565. [Google Scholar] [CrossRef]
- Li, B.; Teunissen, P.J.G. High dimensional integer ambiguity resolution: A first comparison between LAMBDA and Bernese. J. Navig. 2011, 64, S192–S210. [Google Scholar] [CrossRef]
- Verhagen, S. The GNSS Integer Ambiguities: Estimation and Validation. Ph.D. Thesis, Delft University of Technology, Delft, The Netherlands, 2005. [Google Scholar]
- Teunissen, P.J.G.; Verhagen, S. The GNSS ambiguity ratio-test revisited: A better way of using it. Surv. Rev. 2009, 41, 138–151. [Google Scholar] [CrossRef]
- Li, H.; Xu, T.; Li, B.; Huang, S.; Wang, J. A new differential code bias (C1–P1) estimation method and its performance evaluation. GPS Solut. 2016, 20, 321–329. [Google Scholar] [CrossRef]
- Dow, J.; Neilan, R.; Rizos, C. The International GNSS Service in a changing landscape of Global Navigation Satellite Systems. J. Geod. 2009, 83, 191–198. [Google Scholar] [CrossRef] [Green Version]
- Hadas, T.; Jaroslaw, B. IGS RTS precise orbits and clocks verification and quality degradation over time. GPS Solut. 2015, 19, 93–105. [Google Scholar] [CrossRef]
- Chen, Y.; Yuan, Y.; Zhang, B.; Liu, T.; Ding, W.; Ai, Q. A modified mix-differenced approach for estimating multi-GNSS real-time satellite clock offsets. GPS Solut. 2018, 22, 72. [Google Scholar] [CrossRef]
- Kazmierski, K.; Sośnica, S.; Hadas, T. Quality assessment of multi-GNSS orbits and clocks for real-time precise point positioning. GPS Solut. 2018, 22, 11. [Google Scholar] [CrossRef]









| Model | Settings | |
|---|---|---|
| Measurements | Ionosphere-free code and phase combination | |
| Adjustment | Least square | |
| Weighting | Elevation-dependent function | |
| Corrections | DCB(P1-C1) | Products provided by CODE |
| Tides corrections | Solid tide and ocean tide correction | |
| Phase center variation(PCV) | Absolute IGS 08 correction mode | |
| Relativity | Corrected | |
| Parameters | Station coordinates | Estimated |
| Troposphere | Correction: Saastamoinen model Residual: Estimate as piece wise mode | |
| Receiver clock error | Solved for at each epoch as white noise | |
| Phase ambiguity | Float and fixing results |
| Strategy | 1 h | 2 h | 4 h | ||||||
|---|---|---|---|---|---|---|---|---|---|
| North | East | Up | North | East | Up | North | East | Up | |
| #1 | 2.30 | 2.87 | 3.12 | 1.92 | 2.01 | 2.27 | 0.80 | 1.01 | 1.23 |
| #2 | 2.03 | 2.41 | 2.75 | 1.43 | 1.55 | 2.09 | 0.62 | 0.86 | 0.91 |
| #3 | 1.76 | 2.22 | 2.56 | 1.41 | 1.52 | 1.83 | 0.53 | 0.58 | 0.77 |
| Improvement (%) | 12 | 16 | 12 | 26 | 23 | 8 | 23 | 15 | 26 |
| 23 | 23 | 18 | 27 | 24 | 19 | 34 | 43 | 37 | |
| Strategy | 1 h | 2 h | 4 h | ||||||
|---|---|---|---|---|---|---|---|---|---|
| North | East | Up | North | East | Up | North | East | Up | |
| #1 | 2.28 | 2.89 | 3.15 | 1.93 | 2.03 | 2.25 | 0.80 | 1.01 | 1.23 |
| #2 | 2.09 | 2.44 | 2.79 | 1.47 | 1.58 | 2.10 | 0.62 | 0.86 | 0.91 |
| #3 | 1.71 | 2.19 | 2.53 | 1.38 | 1.49 | 1.83 | 0.53 | 0.58 | 0.77 |
| Improvement (%) | 8 | 16 | 11 | 24 | 22 | 7 | 23 | 15 | 26 |
| 25 | 24 | 20 | 28 | 27 | 19 | 34 | 43 | 37 | |
| Strategy | 1 h | 2 h | 4 h | ||||||
|---|---|---|---|---|---|---|---|---|---|
| North | East | Up | North | East | Up | North | East | Up | |
| #1 | 0.93 | 0.95 | 0.99 | 0.85 | 0.92 | 0.97 | 0.77 | 0.65 | 0.25 |
| #2 | 0. 89 | 0.90 | 0.91 | 0.80 | 0.88 | 0.91 | 0.76 | 0.64 | 0.22 |
| #3 | 0.84 | 0.85 | 0.89 | 0.78 | 0.82 | 0.88 | 0.72 | 0.60 | 0.20 |
| Improvement (%) | 4 | 5 | 8 | 6 | 4 | 6 | 1 | 2 | 12 |
| 10 | 11 | 10 | 8 | 11 | 9 | 6 | 8 | 20 | |
| Strategy | 1 h | 2 h | 4 h | ||||||
|---|---|---|---|---|---|---|---|---|---|
| North | East | Up | North | East | Up | North | East | Up | |
| #1 | 0.94 | 0.96 | 0.98 | 0.86 | 0.91 | 0.98 | 0.78 | 0.64 | 0.26 |
| #2 | 0.90 | 0.90 | 0.89 | 0.81 | 0.87 | 0.93 | 0.76 | 0.63 | 0.23 |
| #3 | 0.85 | 0.87 | 0.89 | 0.77 | 0.82 | 0.89 | 0.71 | 0.62 | 0.19 |
| Improvement (%) | 4 | 6 | 9 | 6 | 4 | 5 | 3 | 2 | 12 |
| 10 | 9 | 9 | 10 | 10 | 9 | 9 | 3 | 27 | |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, H.; Xiao, J.; Zhang, S.; Zhou, J.; Wang, J. Introduction of the Double-Differenced Ambiguity Resolution into Precise Point Positioning. Remote Sens. 2018, 10, 1779. https://doi.org/10.3390/rs10111779
Li H, Xiao J, Zhang S, Zhou J, Wang J. Introduction of the Double-Differenced Ambiguity Resolution into Precise Point Positioning. Remote Sensing. 2018; 10(11):1779. https://doi.org/10.3390/rs10111779
Chicago/Turabian StyleLi, Haojun, Jingxin Xiao, Shoujian Zhang, Jin Zhou, and Jiexian Wang. 2018. "Introduction of the Double-Differenced Ambiguity Resolution into Precise Point Positioning" Remote Sensing 10, no. 11: 1779. https://doi.org/10.3390/rs10111779