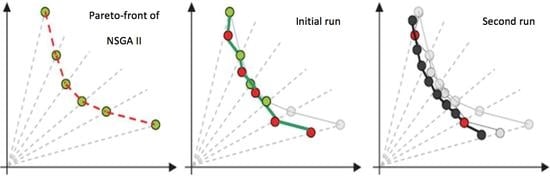
2-Phase NSGA II: An Optimized Reward and Risk Measurements Algorithm in Portfolio Optimization
Abstract
:1. Introduction
2. Related Work
3. Statement of Problem and Notation
- (i)
- for , This limitation ensures that at least one asset from each class should be chosen;
- (ii)
- , which means the portfolio should have more assets that classes (this note is concluded from the first point).
4. Methodologies
4.1. NSGA II Algorithm
4.2. The Proposed 2-Phase NSGA II Algorithm
4.3. The Algorithms Procedure
- (1)
- Set and produce the random population of size N.
- (2)
- Assess the objective functions and sort the solutions based on dominance and non-dominance relation operator.
- (3)
- Select the solutions as parents based on uniform selection.
- (4)
- Affect the selected solutions by crossover and mutation operators to produce offspring population of size N.
- (5)
- Evaluate the new offspring based on objective functions.
- (6)
- and sort the solution based on dominance and non-dominance relation (swift non-dominated kind) and make fronts (, , …).
- (7)
- and .
- (8)
- Until , , .
- (9)
- If , calculate crowding distance for all solutions in .
- (10)
- Sort (, )
- (11)
- (12)
- Stopping criteria: End the algorithm if the stopping criterion is met; otherwise, go to step 2.
- (1)
- After normalizing array A, the weight of one or more classes may not be within the lower and upper limits. For overbearing this problem, the weight of that class or those classes should be calculated again using Equation (11). This process is continued until the weight of all classes lies within their lower and upper limits.
- (2)
- The weight of each class should equal the sum of the weights of the assets existed in that class. When there is only one asset in a given class, it is clear that the weight of this asset is unlikely to be equal to the weight of the class that it belongs to. Therefore, we consider the weight of the class for the asset and investigate whether this new weight satisfies quantity constraint. If this provision is not confirmed, the weight is calculated for the second time. If the weight violates the upper limit, the new weight is replaced with upper limit and the other weights are normalized again. This process continues until all weights are located in the lower and upper bounds span.
- (3)
- Given the fact that selecting at least one asset from each class is essential in the model (), we are assured of choosing one asset from each class at the same time as filling the cells of B chromosome.
4.4. Genetic Operators
5. Performance Evaluation
5.1. Scenario Description
5.1.1. Data Sets
5.1.2. Comparison Metrics
- (1)
- (2)
- NPS: number of solutions in the Pareto-front;
- (3)
- MS: the maximum spread that is the Euclidean distance between boundary solutions;
- (4)
- S: the spacing which is proceeded to calculate the space between two adjacent solutions;
- (5)
- CS: the coverage set which is used to survey the preference of the algorithms.
5.1.3. Parameter Settings
5.2. Experimental Results
Analysis of the Results
6. Conclusions and Future Developments
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Markowitz, H. Portfolio selection. J. Financ. 1952, 7, 77–91. [Google Scholar]
- Markowitz, H.M. Portfolio Selection: Efficient Diversification of Investments; Yale University Press: New Haven, CT, USA, 1968; Volume 16. [Google Scholar]
- Chang, T.J.; Meade, N.; Beasley, J.E.; Sharaiha, Y.M. Heuristics for cardinality constrained portfolio optimisation. Comput. Oper. Res. 2000, 27, 1271–1302. [Google Scholar] [CrossRef]
- Crama, Y.; Schyns, M. Simulated annealing for complex portfolio selection problems. Eur. J. Oper. Res. 2003, 150, 546–571. [Google Scholar] [CrossRef]
- Gilli, M.; Këllezi, E. A global optimization heuristic for portfolio choice with VaR and expected shortfall. In Computational Methods in Decision-Making, Economics and Finance; Springer: Berlin, Germany, 2002; pp. 167–183. [Google Scholar]
- Shojafar, M.; Cordeschi, N.; Baccarelli, E. Energy-efficient adaptive resource management for real-time vehicular cloud services. IEEE Trans. Cloud Comput. 2016, 99, 1–14. [Google Scholar] [CrossRef]
- Metawa, N.; Hassan, M.K.; Elhoseny, M. Genetic algorithm based model for optimizing bank lending decisions. Expert Syst. Appl. 2017, 80, 75–82. [Google Scholar] [CrossRef]
- Dueck, G.; Winker, P. New concepts and algorithms for portfolio choice. Appl. Stoch. Models Data Anal. 1992, 8, 159–178. [Google Scholar] [CrossRef]
- Celikyurt, U.; Özekici, S. Multiperiod portfolio optimization models in stochastic markets using the mean–variance approach. Eur. J. Oper. Res. 2007, 179, 186–202. [Google Scholar] [CrossRef]
- Allen, L.; Saunders, A. Incorporating systemic influences into risk measurements: A survey of the literature. J. Financ. Serv. Res. 2004, 26, 161–191. [Google Scholar] [CrossRef]
- Anagnostopoulos, K.; Mamanis, G. A portfolio optimization model with three objectives and discrete variables. Comput. Oper. Res. 2010, 37, 1285–1297. [Google Scholar] [CrossRef]
- Chiam, S.; Tan, K.; Al Mamum, A. Evolutionary multi-objective portfolio optimization in practical context. Int. J. Autom. Comput. 2008, 5, 67–80. [Google Scholar] [CrossRef]
- Duellmann, K.; Masschelein, N. A tractable model to measure sector concentration risk in credit portfolios. J. Financ. Serv. Res. 2007, 32, 55–79. [Google Scholar] [CrossRef]
- Pelusi, D.; Tivegna, M.; Ippoliti, P. Improving the profitability of technical analysis through intelligent algorithms. J. Interdiscip. Math. 2013, 16, 203–215. [Google Scholar] [CrossRef]
- Pelusi, D.; Mascella, R.; Tallini, L. Revised gravitational search algorithms based on evolutionary-fuzzy systems. Algorithms 2017, 10, 44. [Google Scholar] [CrossRef]
- Deng, G.F.; Lin, W.T.; Lo, C.C. Markowitz-based portfolio selection with cardinality constraints using improved particle swarm optimization. Expert Syst. Appl. 2012, 39, 4558–4566. [Google Scholar] [CrossRef]
- Lin, C.C.; Liu, Y.T. Genetic algorithms for portfolio selection problems with minimum transaction lots. Eur. J. Oper. Res. 2008, 185, 393–404. [Google Scholar] [CrossRef]
- Fernández, A.; Gómez, S. Portfolio selection using neural networks. Comput. Oper. Res. 2007, 34, 1177–1191. [Google Scholar] [CrossRef]
- Chang, T.J.; Yang, S.C.; Chang, K.J. Portfolio optimization problems in different risk measures using genetic algorithm. Expert Syst. Appl. 2009, 36, 10529–10537. [Google Scholar] [CrossRef]
- Yu, L.; Wang, S.; Lai, K.K. Neural network-based mean–variance–skewness model for portfolio selection. Comput. Oper. Res. 2008, 35, 34–46. [Google Scholar] [CrossRef]
- Cura, T. Particle swarm optimization approach to portfolio optimization. Nonlinear Anal. Real World Appl. 2009, 10, 2396–2406. [Google Scholar] [CrossRef]
- Chen, W.; Zhang, W.G. The admissible portfolio selection problem with transaction costs and an improved PSO algorithm. Phys. A Stat. Mech. Appl. 2010, 389, 2070–2076. [Google Scholar] [CrossRef]
- Soleimani, H.; Golmakani, H.R.; Salimi, M.H. Markowitz-based portfolio selection with minimum transaction lots, cardinality constraints and regarding sector capitalization using genetic algorithm. Expert Syst. Appl. 2009, 36, 5058–5063. [Google Scholar] [CrossRef]
- Ong, C.S.; Huang, J.J.; Tzeng, G.H. A novel hybrid model for portfolio selection. Appl. Math. Comput. 2005, 169, 1195–1210. [Google Scholar] [CrossRef]
- Armananzas, R.; Lozano, J.A. A Multiobjective Approach to the Portfolio Optimization Problem. In Proceedings of the IEEE 2005 IEEE Congress on Evolutionary Computation, Edinburgh, Scotland, 2–5 September 2005; pp. 1388–1395. [Google Scholar]
- Diosan, L. A Multi-Objective Evolutionary Approach to the Portfolio Optimization Problem. In Proceedings of the IEEE International Conference on Computational Intelligence for Modelling, Control and Automation and International Conference on Intelligent Agents, Web Technologies and Internet Commerce (CIMCA-IAWTIC’06), Vienna, Austria, 28–30 November 2005; Volume 2, pp. 183–187. [Google Scholar]
- Subbu, R.; Bonissone, P.P.; Eklund, N.; Bollapragada, S.; Chalermkraivuth, K. Multiobjective Financial Portfolio Design: A Hybrid Evolutionary Approach. In Proceedings of the 2005 IEEE Congress on Evolutionary Computation, Edinburgh, UK, 2–5 September 2005; Volume 2, pp. 1722–1729. [Google Scholar]
- Branke, J.; Scheckenbach, B.; Stein, M.; Deb, K.; Schmeck, H. Portfolio optimization with an envelope-based multi-objective evolutionary algorithm. Eur. J. Oper. Res. 2009, 199, 684–693. [Google Scholar] [CrossRef]
- Lwin, K.; Qu, R.; Kendall, G. A learning-guided multi-objective evolutionary algorithm for constrained portfolio optimization. Appl. Soft Comput. 2014, 24, 757–772. [Google Scholar] [CrossRef]
- Hallerbach, W.G.; Spronk, J. The relevance of MCDM for financial decisions. J. Multi-Criteria Decis. Anal. 2002, 11, 187–195. [Google Scholar] [CrossRef]
- Pindoriya, N.; Singh, S.; Singh, S. Multi-objective mean–variance–skewness model for generation portfolio allocation in electricity markets. Electr. Power Syst. Res. 2010, 80, 1314–1321. [Google Scholar] [CrossRef]
- Jana, P.; Roy, T.; Mazumder, S. Multi-objective mean-variance-skewness model for portfolio optimization. Adv. Model. Optim. 2007, 9, 181–193. [Google Scholar]
- Abdelaziz, F.B.; Aouni, B.; El Fayedh, R. Multi-objective stochastic programming for portfolio selection. Eur. J. Oper. Res. 2007, 177, 1811–1823. [Google Scholar] [CrossRef]
- Lo, A.W.; Petrov, C.; Wierzbicki, M. It’s 11 p.m.—Do you know where your liquidity is? The mean-variance-liquidity frontier. World Risk Manag. 2003, 1, 47. [Google Scholar]
- Yakut, E.; Çankal, A. Portfolio Optimzation Using of Metods Multi Objective Genetic Algorithm and Goal Programming: An Application in BIST-30. Bus. Econ. Res. J. 2016, 7, 43–62. [Google Scholar] [CrossRef]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- Anagnostopoulos, K.P.; Mamanis, G. Multiobjective evolutionary algorithms for complex portfolio optimization problems. Comput. Manag. Sci. 2011, 8, 259–279. [Google Scholar] [CrossRef]
- Behnamian, J.; Ghomi, S.F.; Zandieh, M. A multi-phase covering Pareto-optimal front method to multi-objective scheduling in a realistic hybrid flowshop using a hybrid metaheuristic. Expert Syst. Appl. 2009, 36, 11057–11069. [Google Scholar] [CrossRef]




| Problem Index | Data Source | Number of Assets |
|---|---|---|
| Port 1 | Hong Kong, hang seng | 31 |
| Port 2 | German, Dax 100 | 85 |
| Port 3 | British, FTSE 100 | 89 |
| Port 4 | US, S&P 100 | 98 |
| Port 5 | Japanese, Nikkei 225 | 225 |
| Metric | Formula |
|---|---|
| MID | , |
| MS | |
| S | |
| CS |
| Problems | k | M | ||
|---|---|---|---|---|
| Port 1 | 400 | 100 | 10 | 8 |
| Port 2 | 500 | 200 | 20 | 17 |
| Port 3 | 300 | 200 | 20 | 18 |
| Port 4 | 500 | 200 | 20 | 14 |
| Port 5 | 300 | 200 | 30 | 23 |
| Problem Size | Algorithm and Index | ||||
| MID | NPS | ||||
| Port | N | NSGA II | 2-p NSGA II | NSGA II | 2-p NSGA II |
| Port 1 | 31 | 0.28343 | 0.27433 | 273 | 6481 |
| Port 2 | 85 | 0.07428 | 0.07281 | 1451 | 51,032 |
| Port 3 | 89 | 0.13528 | 0.1381 | 1358 | 43,487 |
| Port 4 | 98 | 0.10234 | 0.1011 | 678 | 36,348 |
| Port 5 | 225 | 0.31602 | 0.31365 | 742 | 49,061 |
| MS | S | ||||
| Port | N | NSGA II | 2-p NSGA II | NSGA II | 2-p NSGA II |
| Port 1 | 31 | 0.12025 | 0.11623 | 0.20062 | 0.01591 |
| Port 2 | 85 | 0.06574 | 0.06453 | 0.06887 | 0.00284 |
| Port 3 | 89 | 0.1132 | 0.11276 | 0.15946 | 0.0056 |
| Port 4 | 98 | 0.19875 | 0.19848 | 0.34357 | 0.00777 |
| Port 5 | 225 | 0.31602 | 0.31365 | 0.22209 | 0.00558 |
| C | |||||
| Port | N | NSGA II | 2-p NSGA II | ||
| Port 1 | 31 | 0.00694 | 0.80952 | ||
| Port 2 | 85 | 0.01813 | 0.77739 | ||
| Port 3 | 89 | 0.03507 | 0.8947 | ||
| Port 4 | 98 | 0.01618 | 0.82006 | ||
| Port 5 | 225 | 0.01861 | 0.90701 | ||
| Metric | p-Value |
|---|---|
| MID | 0.852 |
| NPS | 0.000 |
| MS | 0.027 |
| S | 0.000 |
| CS | 0.000 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Eftekharian, S.E.; Shojafar, M.; Shamshirband, S. 2-Phase NSGA II: An Optimized Reward and Risk Measurements Algorithm in Portfolio Optimization. Algorithms 2017, 10, 130. https://doi.org/10.3390/a10040130
Eftekharian SE, Shojafar M, Shamshirband S. 2-Phase NSGA II: An Optimized Reward and Risk Measurements Algorithm in Portfolio Optimization. Algorithms. 2017; 10(4):130. https://doi.org/10.3390/a10040130
Chicago/Turabian StyleEftekharian, Seyedeh Elham, Mohammad Shojafar, and Shahaboddin Shamshirband. 2017. "2-Phase NSGA II: An Optimized Reward and Risk Measurements Algorithm in Portfolio Optimization" Algorithms 10, no. 4: 130. https://doi.org/10.3390/a10040130