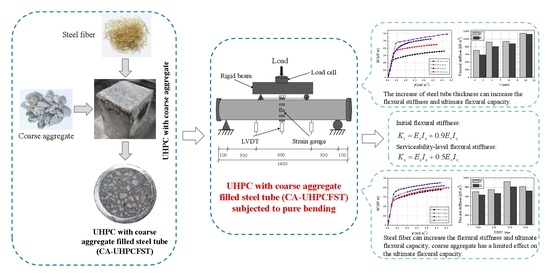
Experimental Investigation of Flexural Behavior of Ultra-High-Performance Concrete with Coarse Aggregate-Filled Steel Tubes
Abstract
:1. Introduction
2. Experimental Program
2.1. Test Design
2.2. Materials Properties
2.2.1. Steel
2.2.2. UHPC with Coarse Aggregate
2.3. Experimental Setup and Loading Procedure
3. Test Results and Discussion
3.1. Failure Modes
3.2. Overall Deflection Curves
3.3. Moment–Curvature Relationship
- (1)
- Elastic stage: the moment increases linearly with the curvature until the moment reaches 70~80% of ultimate flexural capacity. The moment increases sharply in this stage, while the increase of the curvature is mild. The stiffness remains almost constant, while the steel tube and the compression zone of the CA-UHPC infill remain in an elastic state during this stage. When the load reaches 30~40% of ultimate flexural capacity, the tensile stress in the tensile flange of the concrete exceeds the tensile strength, resulting in transverse cracking. With regard to the core CA-UHPC infilled with steel fiber, the steel fiber is able to restrain the initiation and extension of tensile cracks triggered during this stage, thus enhancing the flexural performance of the concrete core.
- (2)
- Elastic–plastic stage: the moment increases moderately while the curvature increases rapidly. The specimen presents nonlinear response as the gradient of the curves decreases. The yield zone at the bottom flange of the steel tube gradually extends to the compression zone, while the top region of the steel tube and the CA-UHPC are still in an elastic state. The yielding of steel tube tensile flange and the cracking of the concrete core in the tensile zone accelerate the degradation of the section flexural stiffness of the CA-UHPCFST beam. The interaction between the steel tube and the UHPC infill is triggered in this stage, and this can restrict the development of cracks in the CA-UHPC core along the height of the section.
- (3)
- Plastic hardening stage: there is a nearly linear relationship between the bending moment and curvature; however, the slope of the curve is much lower than during the elastic stage. The moment increases at a moderate rate, but nevertheless the curvature increases rapidly. Near point C, the top edge of the steel tube has yielded and the compressive top fiber of CA-UHPC infill is crushed. The stiffness of the specimen decreases dramatically due to the gradual yielding of the steel tube from the tensile flange and the compression edge to the neutral axis. Until the termination of the test, the curve still increases continually, and no distinct softening stage can be observed; the increasing rate of moment in plastic hardening stage is distinctly higher than that of the normal- and high-strength concrete-filled steel tubes or stainless steel tubes. It is demonstrated that the CA-UHPCFST beams under pure bending have better ductility than conventional CFSTs [18,34,35]. This may be ascribed to the higher flexural strength of UHPC and the interaction effect between the steel tube and the CA-UHPC core, where the CA-UHPC prevents the inward local buckling of the steel tube, and accordingly, the further strength degradation and cracking of the core CA-UHPC is restricted due to the confinement provided by the external steel tube.
3.4. Moment–Strain Relationship
3.5. Ultimate Flexural Capacity
3.6. Flexural Stiffness
3.7. Ductility and Energy Dissipation Capacity
3.8. Strain Ratio
4. Design Guidelines
4.1. Comparisons of Flexural Stiffness
4.2. Comparisons of Ultimate Flexural Capacity
5. Conclusions
- (1)
- All the CA-UHPCFST members behaved in a good ductile manner. The failure mode of specimens was similar to that of conventional CFST specimens. The addition of steel fiber had a limited effect on the global failure mode, whereas it was able to effectively reduce the number and depth of the tensile cracks, as well as mitigating the crushing in the compressive zone of the CA-UHPC infill.
- (2)
- The flexural stiffness, ultimate flexural capacity and hardening stage flexural moment were significantly enhanced with increased steel tube thickness. The increase in concrete strength for CA-UHPC without steel fiber had a limited effect on the flexural capacity. The incorporation of steel fiber was able to moderately increase the ultimate flexural capacity of the CA-UHPCFST members as well as lengthen the elastic stage of moment-versus-curvature curve.
- (3)
- The yield flexural moment of the CA-UHPCFST members under bending was approximately 0.7 times the ultimate flexural strength. The confinement effect in the compressive zone and the centroidal plane was triggered after the specimen entered the elastic–plastic stage, while the confinement effect in the tensile flange was minor or even negligible throughout the whole loading process.
- (4)
- Two empirical formulas were developed to predict the initial flexural stiffness and serviceability-level flexural stiffness of circular CA-UHPCFSTs. EC 4, AIJ, AS 5100 presented conservative results for the initial flexural stiffness, BS 5400-5 and AISC/LRFD gave the most accurate prediction on the value of Ki. Additionally, EC 4, AS 5100, BS 5400-5 and AISC/LRFD overestimated the serviceability-level flexural stiffness.
- (5)
- The current design rules are imprecise for calculating the ultimate flexural moment of CA-UHPCFSTs, with AIJ and BS 5400 presenting conservative results for the flexural capacity of circular CA-UHPCFST beams subjected to pure bending load, while EC 4, GB 50936, and the formula proposed by Han overestimate the ultimate flexural capacity. Further research is still required to propose accurate design formulas for the ultimate flexural capacity of CA-UHPCFSTs.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ellobody, E.; Young, B.; Lam, D. Behaviour of Normal and High Strength Concrete-Filled Compact Steel Tube Circular Stub Columns. J. Constr. Steel Res. 2006, 62, 706–715. [Google Scholar] [CrossRef]
- Yoo, D.; Banthia, N. Mechanical Properties of Ultra-High-Performance Fiber-Reinforced Concrete: A Review. Cem. Concr. Compos. 2016, 73, 267–280. [Google Scholar] [CrossRef]
- Yoo, D.; Kim, S.; Park, J. Comparative Flexural Behavior of Ultra-High-Performance Concrete Reinforced with Hybrid Straight Steel Fibers. Constr. Build. Mater. 2017, 132, 219–229. [Google Scholar] [CrossRef]
- Yoo, D.; Yoon, Y. Structural Performance of Ultra-High-Performance Concrete Beams with Different Steel Fibers. Eng. Struct. 2015, 102, 409–423. [Google Scholar] [CrossRef]
- Hassan, A.M.T.; Jones, S.W.; Mahmud, G.H. Experimental Test Methods to Determine the Uniaxial Tensile and Compressive Behaviour of Ultra High Performance Fibre Reinforced Concrete (UHPFRC). Constr. Build. Mater. 2012, 37, 874–882. [Google Scholar] [CrossRef]
- Xu, L.; Wu, F.; Chi, Y.; Cheng, P.; Zeng, Y.; Chen, Q. Effects of Coarse Aggregate and Steel Fibre Contents On Mechanical Properties of High Performance Concrete. Constr. Build. Mater. 2019, 206, 97–110. [Google Scholar]
- Hannawi, K.; Bian, H.; Prince-Agbodjan, W.; Raghavan, B. Effect of Different Types of Fibers On the Microstructure and the Mechanical Behavior of Ultra-High Performance Fiber-Reinforced Concretes. Compos. Part B Eng. 2016, 86, 214–220. [Google Scholar] [CrossRef] [Green Version]
- Wang, Q.; Shi, Q.; Lui, E.M.; Xu, Z. Axial Compressive Behavior of Reactive Powder Concrete-Filled Circular Steel Tube Stub Columns. J. Constr. Steel Res. 2019, 153, 42–54. [Google Scholar] [CrossRef]
- Hoang, A.L.; Fehling, E.; Lai, B.; Thai, D.; Chau, N.V. Experimental study on structural performance of UHPC and UHPFRC columns confined with steel tube. Eng. Struct. 2019, 187, 457–477. [Google Scholar] [CrossRef]
- Xiong, M.; Xiong, D.; Liew, J.Y.R. Behaviour of Steel Tubular Members Infilled with Ultra High Strength Concrete. J. Constr. Steel Res. 2017, 138, 168–183. [Google Scholar] [CrossRef]
- Guler, S.; Çopur, A.; Aydogan, M. Axial capacity and ductility of circular UHPC-filled steel tube columns. Mag. Concr. Res. 2013, 65, 898–905. [Google Scholar] [CrossRef]
- An, L.H.; Fehling, E. Analysis of Circular Steel Tube Confined UHPC Stub Columns. Steel Compos. Struct. 2017, 23, 669–682. [Google Scholar]
- Huang, W.; Fan, Z.; Shen, P.; Lu, L.; Zhou, Z. Experimental and Numerical Study On the Compressive Behavior of Micro-Expansive Ultra-High-Performance Concrete-Filled Steel Tube Columns. Constr. Build. Mater. 2020, 254, 119150. [Google Scholar] [CrossRef]
- Chen, S.; Zhang, R.; Jia, L.; Wang, J.; Gu, P. Structural Behavior of UHPC Filled Steel Tube Columns Under Axial Loading. Thin Wall. Struct. 2018, 130, 550–563. [Google Scholar] [CrossRef]
- Yan, Y.; Xu, L.; Li, B.; Chi, Y.; Yu, M.; Zhou, K.; Song, Y. Axial Behavior of Ultra-High Performance Concrete (UHPC) Filled Stocky Steel Tubes with Square Sections. J. Constr. Steel Res. 2019, 158, 417–428. [Google Scholar] [CrossRef]
- Xu, L.; Lu, Q.; Chi, Y.; Yang, Y.; Yu, M.; Yan, Y. Axial Compressive Performance of UHPC Filled Steel Tube Stub Columns Containing Steel-Polypropylene Hybrid Fiber. Constr. Build. Mater. 2019, 204, 754–767. [Google Scholar] [CrossRef]
- Wei, J.; Xie, Z.; Zhang, W.; Luo, X.; Yang, Y.; Chen, B. Experimental Study On Circular Steel Tube-Confined Reinforced UHPC Columns Under Axial Loading. Eng. Struct. 2021, 230, 111599. [Google Scholar] [CrossRef]
- Xiong, M.; Xiong, D.; Liew, J.Y.R. Flexural Performance of Concrete Filled Tubes with High Tensile Steel and Ultra-High Strength Concrete. J. Constr. Steel Res. 2017, 132, 191–202. [Google Scholar] [CrossRef]
- EN 1994-1-1. Eurocode 4: Design of Composite Steel and Concrete Structures—Part 1-1: General Rules and Rules for Buildings; European Committee for Standardization: Brussels, Belgium, 2004. [Google Scholar]
- Guler, S.; Copur, A.; Aydogan, M. Flexural Behaviour of Square UHPC-filled Hollow Steel Section Beams. Struct. Eng. Mech. 2012, 43, 225–237. [Google Scholar] [CrossRef]
- Li, J.; Deng, Z.; Sun, T. Flexural Behavior of Ultra-High Performance Concrete Filled High-Strength Steel Tube. Struct. Concr. 2021, 22, 1688–1707. [Google Scholar] [CrossRef]
- Yang, I.; Joh, C.; Kim, B. Flexural Response Predictions for Ultra-High-Performance Fibre-Reinforced Concrete Beams. Mag. Concr. Res. 2012, 64, 113–127. [Google Scholar] [CrossRef]
- Wu, Z.; Khayat, K.H.; Shi, C. How Do Fiber Shape and Matrix Composition Affect Fiber Pullout Behavior and Flexural Properties of UHPC? Cem. Concr. Comp. 2018, 90, 193–201. [Google Scholar] [CrossRef] [Green Version]
- AISC/LRFD. Load and Resistance Factor Design Specification for Structural Steel Buildings; American Institute of Steel Construction: Chicago, IL, USA, 2005. [Google Scholar]
- AIJ. Recommendations for Design and Structures of Concrete Filled Steel Tubular Structures; Architectural Institute of Japan: Tokyo, Japan, 1997. [Google Scholar]
- AS 5100.6. Bridge Design—Part 6: Steel and Composite Construction; Australian Standards: Sydney, Australia, 2004. [Google Scholar]
- BS 5400-5. Steel, Concrete and Composite Bridges—Part 5: Code of Practice for Design of Composite Bridges; British Standards Institution: London, UK, 2005. [Google Scholar]
- GB 50936-2014. Technical Code for Concrete-Filled Steel Tubular Structures; Architecture & Buliding Press: Beijing, China, 2014. (In Chinese) [Google Scholar]
- GB/T228. 1–2010. Metallic Materials-Tensile Testing—Part1: Method of Test at Room Temperature; China Standard Press: Beijing, China, 2010. (In Chinese) [Google Scholar]
- Lu, Y.; Liu, Z.; Li, S.; Li, W. Behavior of steel fibers reinforced self-stressing and self-compacting concrete-filled steel tube subjected to bending. Constr. Build. Mater. 2017, 156, 639–651. [Google Scholar] [CrossRef]
- Han, L. Flexural behaviour of concrete-filled steel tubes. J. Constr. Steel Res. 2004, 60, 313–337. [Google Scholar] [CrossRef]
- Al-Shaar, A.A.M.; Göğüş, M.T. Flexural behavior of lightweight concrete and self-compacting concrete-filled steel tube beams. J. Constr. Steel Res. 2018, 149, 153–164. [Google Scholar] [CrossRef]
- Li, G.; Liu, D.; Yang, Z.; Zhang, C. Flexural Behavior of High Strength Concrete Filled High Strength Square Steel Tube. J. Constr. Steel Res. 2017, 128, 732–744. [Google Scholar] [CrossRef]
- Han, L.; Lu, H.; Yao, G.; Liao, F. Further Study On the Flexural Behaviour of Concrete-Filled Steel Tubes. J. Constr. Steel Res. 2006, 62, 554–565. [Google Scholar] [CrossRef]
- Chen, Y.; Feng, R.; Wang, L. Flexural Behaviour of Concrete-Filled Stainless Steel SHS and RHS Tubes. Eng. Struct. 2017, 134, 159–171. [Google Scholar] [CrossRef]
- Wu, F.; Xu, L.; Chi, Y.; Zeng, Y.; Deng, F.; Chen, Q. Compressive and flexural properties of ultra-high performance fiber-reinforced cementitious composite: The effect of coarse aggregate. Compos. Struct. 2020, 236, 111810. [Google Scholar] [CrossRef]
- Zhang, T.; Gong, Y.; Ding, F.; Liu, X.; Yu, Z. Experimental and Numerical Investigation On the Flexural Behavior of Concrete-Filled Elliptical Steel Tube (CFET). J. Build. Eng. 2021, 41, 102412. [Google Scholar] [CrossRef]














| Specimen | L (mm) | D (mm) | t (mm) | fy (MPa) | As (mm2) | fck (MPa) | Ac (mm2) | ξ | Mu (kN∙m) | Ke (kN∙m2) | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Ki | Ks | ||||||||||
| BC20S6 | 1400 | 114 | 6 | 406 | 2035 | 101 | 8167 | 1.00 | 30.52 | 709 | 636 |
| BC30S6 | 1400 | 114 | 6 | 406 | 2035 | 108 | 8167 | 0.94 | 30.66 | 749 | 671 |
| BC32S6 | 1400 | 114 | 6 | 406 | 2035 | 124 | 8167 | 0.82 | 38.52 | 924 | 809 |
| BC02S6 | 1400 | 114 | 6 | 406 | 2035 | 112 | 8167 | 0.90 | 33.68 | 819 | 728 |
| BC32S4.5 | 1400 | 114 | 4.5 | 420 | 1547 | 124 | 8655 | 0.61 | 27.72 | 706 | 587 |
| BC32S8 | 1400 | 114 | 8 | 400 | 2662 | 124 | 7539 | 1.14 | 43.66 | 940 | 879 |
| BC32S10 | 1400 | 114 | 10 | 429 | 3285 | 124 | 6936 | 1.63 | 53.24 | 1154 | 1132 |
| Thickness (mm) | fy (MPa) | fu (MPa) | Es (GPa) |
|---|---|---|---|
| 4.5 | 420 | 603 | 205 |
| 6 | 406 | 589 | 206 |
| 8 | 400 | 592 | 206 |
| 10 | 429 | 587 | 205 |
| Mix | Content (kg/m3) | fcu (MPa) | fck (MPa) | Ec (GPa) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Cement | Silica Fume | Fly Ash | Steel Fiber | PPF | Water | SP | Sand | Granite | ||||
| C20 | 599.24 | 138.29 | 184.38 | 0.0 | 0.9 | 165.94 | 23.05 | 1014.10 | 430 | 113 | 101 | 39 |
| C30 | 493.49 | 113.88 | 151.84 | 0.0 | 0.9 | 136.66 | 18.98 | 835.14 | 817 | 117 | 108 | 42 |
| C32 | 449.22 | 103.67 | 138.22 | 157.0 | 0.9 | 124.40 | 17.28 | 760.22 | 817 | 139 | 124 | 48 |
| C02 | 660.72 | 152.47 | 203.30 | 157.0 | 0.9 | 182.97 | 25.41 | 1118.13 | 0 | 126 | 112 | 41 |
| Composition | Na2O | MgO | Al2O3 | SiO2 | SO3 | Fe2O3 | P2O5 | CaO | K2O | MnO | ZnO | SrO |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Cement | 0.079 | 2.14 | 4.5 | 19.58 | 3.06 | 3.119 | 0.128 | 64.94 | 0.75 | 0.127 | 0.024 | 0.148 |
| Silica fume | 0.068 | 0.224 | 0.354 | 92.87 | 1.26 | 0.113 | 0.11 | 0.213 | 0.332 | 0.008 | 0.019 | 0.005 |
| Fly ash | 0.552 | 0.575 | 30.63 | 48.74 | 0.706 | 2.611 | 0.247 | 2.44 | 1.25 | 0.016 | 0.013 | 0.060 |
| Specimen | My (kN∙m) | Mu (kN∙m) | δy (mm) | δu (mm) | Ey (kN∙m) | Eu (kN∙m) | My/Mu | μ = δu/δy | Eu/Ey |
|---|---|---|---|---|---|---|---|---|---|
| BC20S6 | 20.04 | 30.52 | 5.14 | 20.22 | 254.42 | 2313.45 | 0.66 | 3.93 | 9.09 |
| BC30S6 | 20.8 | 30.66 | 5.63 | 20.43 | 277.05 | 2330.89 | 0.68 | 3.63 | 8.41 |
| BC32S6 | 28.96 | 38.52 | 6.28 | 20.04 | 464.46 | 2845.67 | 0.75 | 3.19 | 6.13 |
| BC02S6 | 22.63 | 33.68 | 5.92 | 21.16 | 325.15 | 2562.51 | 0.67 | 3.57 | 7.88 |
| BC32S4.5 | 18.91 | 27.72 | 5.63 | 21.41 | 259.34 | 2264.70 | 0.68 | 3.80 | 8.73 |
| BC32S8 | 32.72 | 43.66 | 8.34 | 23.78 | 640.45 | 3561.25 | 0.75 | 2.85 | 5.56 |
| BC32S10 | 38.52 | 53.24 | 10.56 | 23.70 | 944.75 | 4072.25 | 0.72 | 2.24 | 4.31 |
| Design Codes | Formula |
| EC 4 (2005) [19] | |
| AISC/LRFD (1999) [24] | |
| AS 5100.6 (2004) [26] | |
| AIJ (1997) [25] | |
| BS 5400-5 (2005) [27], GB 50936 (2014) [28] |
| Specimen Label | Ki (kN∙m2) | EC 4 | AIJ | AS 5100 | BS 5400 | AISC/LRFD | Equation (6) | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Kic | Kic/Ki | Kic | Kic/Ki | Kic | Kic/Ki | Kic | Kic/Ki | Kic | Kic/Ki | Kic | Kic/Ki | ||
| BC20S6 | 707 | 730 | 1.03 | 652 | 0.92 | 728 | 1.03 | 809 | 1.14 | 769 | 1.09 | 789 | 1.12 |
| BC30S6 | 749 | 732 | 0.98 | 653 | 0.87 | 730 | 0.98 | 811 | 1.08 | 772 | 1.03 | 792 | 1.06 |
| BC23S6 | 924 | 760 | 0.82 | 662 | 0.72 | 772 | 0.84 | 858 | 0.93 | 809 | 0.87 | 833 | 0.90 |
| BC02S6 | 819 | 707 | 0.86 | 644 | 0.79 | 693 | 0.85 | 770 | 0.94 | 739 | 0.90 | 754 | 0.92 |
| BC23S4.5 | 706 | 643 | 0.91 | 533 | 0.76 | 678 | 0.96 | 753 | 1.07 | 698 | 0.99 | 726 | 1.03 |
| BC23S8 | 940 | 900 | 0.96 | 816 | 0.87 | 885 | 0.94 | 983 | 1.05 | 942 | 1.00 | 963 | 1.02 |
| BC23S10 | 1116 | 1024 | 0.92 | 953 | 0.85 | 985 | 0.88 | 1094 | 0.98 | 1059 | 0.95 | 1077 | 0.97 |
| Mean value | 0.926 | 0.825 | 0.925 | 1.027 | 0.977 | 1.002 | |||||||
| COV | 0.077 | 0.090 | 0.078 | 0.078 | 0.076 | 0.077 | |||||||
| Specimen Label | Ks (kN∙m2) | EC 4 | AIJ | AS 5100 | BS 5400 | AISC/LRFD | Equation (7) | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Ksc | Ksc/Ks | Ksc | Ksc/Ks | Ksc | Ksc/Ks | Ksc | Ksc/Ks | Ksc | Ksc/Ks | Ksc | Ksc/Ks | ||
| BC20S6 | 636 | 730 | 1.15 | 652 | 1.02 | 728 | 1.14 | 809 | 1.27 | 769 | 1.21 | 711 | 1.12 |
| BC30S6 | 671 | 732 | 1.09 | 653 | 0.97 | 730 | 1.09 | 811 | 1.21 | 772 | 1.15 | 712 | 1.06 |
| BC23S6 | 809 | 760 | 0.94 | 662 | 0.82 | 772 | 0.95 | 858 | 1.06 | 809 | 1.00 | 735 | 0.91 |
| BC02S6 | 728 | 707 | 0.97 | 644 | 0.89 | 693 | 0.95 | 770 | 1.06 | 739 | 1.02 | 692 | 0.95 |
| BC23S4.5 | 587 | 643 | 1.10 | 533 | 0.91 | 678 | 1.15 | 753 | 1.28 | 698 | 1.19 | 616 | 1.05 |
| BC23S8 | 879 | 900 | 1.02 | 816 | 0.93 | 885 | 1.01 | 983 | 1.12 | 942 | 1.07 | 879 | 1.00 |
| BC23S10 | 1132 | 1024 | 0.90 | 953 | 0.84 | 985 | 0.87 | 1094 | 0.97 | 1059 | 0.94 | 1006 | 0.89 |
| Mean value | 1.025 | 0.912 | 1.024 | 1.138 | 1.082 | 0.997 | |||||||
| COV | 0.088 | 0.079 | 0.105 | 0.105 | 0.096 | 0.085 | |||||||
| Codes | Formulation |
| EC4 [19] | |
| AIJ [25] | |
| BS 5400-5 [27] | |
| GB 50936 [28] | |
| Han [34] |
| Specimen Label | Mu (kN∙m) | EC 4 | AIJ | BS 5400-5 | GB 50936 | Han | |||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Muc | Muc/Mu | Muc | Muc/Mu | Muc | Muc/Mu | Muc | Muc/Mu | Muc | Muc/Mu | ||
| BC20S6 | 30.5 | 41.5 | 1.36 | 29.5 | 0.97 | 29.5 | 0.97 | 38.6 | 1.27 | 36.4 | 1.19 |
| BC30S6 | 30.6 | 41.5 | 1.35 | 29.5 | 0.96 | 29.7 | 0.97 | 39.1 | 1.28 | 36.6 | 1.19 |
| BC32S6 | 38.5 | 41.7 | 1.08 | 29.5 | 0.77 | 30.1 | 0.78 | 41.3 | 1.07 | 37.6 | 0.98 |
| BC02S6 | 33.7 | 41.6 | 1.23 | 29.5 | 0.88 | 29.9 | 0.89 | 39.9 | 1.19 | 36.9 | 1.10 |
| BC32S4.5 | 27.7 | 33.5 | 1.21 | 23.2 | 0.84 | 23.9 | 0.86 | 36.8 | 1.33 | 29.6 | 1.07 |
| BC32S8 | 43.6 | 52.3 | 1.20 | 38.1 | 0.87 | 38.2 | 0.87 | 42.7 | 0.98 | 49.9 | 1.14 |
| BC32S10 | 53.2 | 67.1 | 1.26 | 50.1 | 0.94 | 48.9 | 0.92 | 32.6 | 0.61 | 68.8 | 1.29 |
| Mean value | 1.242 | 0.890 | 0.895 | 1.103 | 1.137 | ||||||
| COV | 0.077 | 0.083 | 0.073 | 0.226 | 0.090 | ||||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, F.; Zeng, Y.; Li, B.; Lyu, X. Experimental Investigation of Flexural Behavior of Ultra-High-Performance Concrete with Coarse Aggregate-Filled Steel Tubes. Materials 2021, 14, 6354. https://doi.org/10.3390/ma14216354
Wu F, Zeng Y, Li B, Lyu X. Experimental Investigation of Flexural Behavior of Ultra-High-Performance Concrete with Coarse Aggregate-Filled Steel Tubes. Materials. 2021; 14(21):6354. https://doi.org/10.3390/ma14216354
Chicago/Turabian StyleWu, Fanghong, Yanqin Zeng, Ben Li, and Xuetao Lyu. 2021. "Experimental Investigation of Flexural Behavior of Ultra-High-Performance Concrete with Coarse Aggregate-Filled Steel Tubes" Materials 14, no. 21: 6354. https://doi.org/10.3390/ma14216354