Atomic Scale Simulation on the Anti-Pressure and Friction Reduction Mechanisms of MoS2 Monolayer
Abstract
:1. Introduction
2. Simulation Details
3. Results and Discussions
3.1. Indentation Process
3.2. Structural Deformation
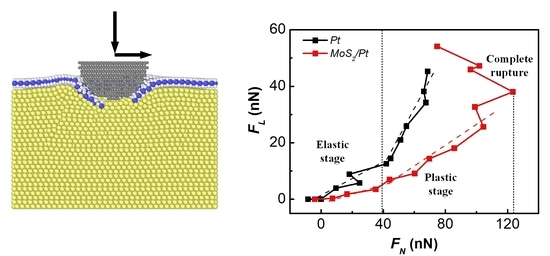
3.3. Scratch Process
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Gupta, A.; Sakthivel, T.; Seal, S. Recent Development in 2D Materials beyond Graphene. Prog. Mater. Sci. 2015, 73, 44–126. [Google Scholar] [CrossRef]
- Zhu, Y.; Murali, S.; Cai, W.; Li, X.; Suk, J.W.; Potts, J.R.; Ruoff, R.S. Graphene and Graphene Oxide: Synthesis, Properties and Applications. Adv. Mater. 2010, 22, 3906–3924. [Google Scholar] [CrossRef] [PubMed]
- Le, D.; Rawal, T.B.; Rahman, T.S. Single-Layer MoS2 with Sulfur Vacancies: Structure and Catalytic Application. J. Phys. Chem. C 2014, 118, 5346–5351. [Google Scholar] [CrossRef]
- Castellanos-Gomez, A. Black Phosphorus: Narrow Gap, Wide Applications. J. Phys. Chem. Lett. 2015, 6, 4280–4291. [Google Scholar] [CrossRef] [PubMed]
- Li, C.; Xie, Z.; Chen, Z.; Cheng, N.; Wang, J.; Zhu, G. Tunable Bandgap and Optical Properties of Black Phosphorene Nanotubes. Materials 2018, 11, 304. [Google Scholar] [CrossRef] [PubMed]
- Nemilentsau, A.; Low, T.; Hanson, G. Anisotropic 2D Materials for Tunable Hyperbolic Plasmonics. Phys. Rev. Lett. 2016, 116, 066804. [Google Scholar] [CrossRef] [PubMed]
- Yang, N.; Yang, D.; Chen, L.; Liu, D.; Cai, M.; Fan, X. A First-Principle Theoretical Study of Mechanical and Electronic Properties in Graphene Single-Walled Carbon Nanotube Junctions. Materials 2017, 10, 1300. [Google Scholar] [CrossRef] [PubMed]
- Lee, S.K.; Rana, K.; Ahn, J.H. Graphene Films for Flexible Organic and Energy Storage Devices. J. Phys. Chem. Lett. 2013, 4, 831–841. [Google Scholar] [CrossRef] [PubMed]
- Soldano, C.; Mahmood, A.; Dujardin, E. Production, Properties and Potential of Graphene. Carbon 2010, 48, 2127–2150. [Google Scholar] [CrossRef]
- Meng, F.; Han, H.; Gao, X.; Yang, C.; Zheng, Z. Experiment Study On Tribological Performances of GNPs/MoS2 Coating. Tribol. Int. 2018, 118, 400–407. [Google Scholar] [CrossRef]
- Luo, J.K.; Fu, Y.Q.; Le, H.R.; Williams, J.A.; Spearing, S.M.; Milne, W.I. Diamond and Diamond-Like Carbon MEMS. J. Micromech. Microeng. 2007, 17, S147. [Google Scholar] [CrossRef]
- Bhushan, B. Nanotribology and Nanomechanics of Mems/Nems and Biomems/Bionems Materials and Devices. Microelectron. Eng. 2007, 84, 387–412. [Google Scholar] [CrossRef]
- Zhong, M.; Zhang, C.; Luo, J.; Lu, X. The Protective Properties of Ultra-Thin Diamond Like Carbon Films for High Density Magnetic Storage Devices. Appl. Surf. Sci. 2009, 256, 322–328. [Google Scholar] [CrossRef]
- Wang, N.; Komvopoulos, K.; Rose, F.; Marchon, B. Structural Stability of Hydrogenated Amorphous Carbon Overcoats Used in Heat-Assisted Magnetic Recording Investigated by Rapid Thermal Annealing. J. Appl. Phys. 2013, 113, 083517. [Google Scholar] [CrossRef]
- Kim, K.; Lee, H.; Lee, C.; Lee, S.; Jang, H.; Ahn, J.; Kim, J.; Lee, H. Chemical Vapor Deposition-Grown Graphene: The Thinnest Solid Lubricant. ACS Nano 2011, 5, 5107–5114. [Google Scholar] [CrossRef] [PubMed]
- Berman, D.; Erdemir, A.; Sumant, A.V. Few Layer Graphene to Reduce Wear and Friction on Sliding Steel Surfaces. Carbon 2013, 54, 454–459. [Google Scholar] [CrossRef]
- Xie, H.; Jiang, B.; Dai, J.; Peng, C.; Li, C.; Li, Q.; Pan, F. Tribological Behaviors of Graphene and Graphene Oxide as Water-Based Lubricant Additives for Magnesium Alloy/Steel Contacts. Materials 2018, 11, 206. [Google Scholar] [CrossRef] [PubMed]
- Berman, D.; Erdemir, A.; Sumant, A.V. Graphene: A New Emerging Lubricant. Mater. Today 2014, 17, 31–42. [Google Scholar] [CrossRef]
- Bertolazzi, S.; Brivio, J.; Kis, A. Stretching and Breaking of Ultrathin MoS2. ACS Nano 2011, 5, 9703–9709. [Google Scholar] [CrossRef] [PubMed]
- Klemenz, A.; Pastewka, L.; Balakrishna, S.G.; Caron, A.; Bennewitz, R.; Moseler, M. Atomic Scale Mechanisms of Friction Reduction and Wear Protection by Graphene. Nano Lett. 2014, 14, 7145–7152. [Google Scholar] [CrossRef] [PubMed]
- Zhao, J.; He, Y.; Wang, Y.; Wang, W.; Yan, L.; Luo, J. An Investigation on the Tribological Properties of Multilayer Graphene and MoS2 Nanosheets as Additives Used in Hydraulic Applications. Tribol. Int. 2016, 97, 14–20. [Google Scholar] [CrossRef]
- Chen, Z.; Liu, X.; Liu, Y.; Gunsel, S.; Luo, J. Ultrathin MoS2 Nanosheets with Superior Extreme Pressure Property as Boundary Lubricants. Sci. Rep. 2015, 5, 12869. [Google Scholar] [CrossRef] [PubMed]
- Dong, Y.; Li, Q.; Martini, A. Molecular Dynamics Simulation of Atomic Friction: A Review and Guide. J. Vac. Sci. Technol. A 2013, 31, 30801. [Google Scholar] [CrossRef]
- Jiang, J.; Park, H.S.; Rabczuk, T. Molecular Dynamics Simulations of Single-Layer Molybdenum Disulphide (MoS2): Stillinger-Weber Parametrization, Mechanical Properties and Thermal Conductivity. J. Appl. Phys. 2013, 114, 064307. [Google Scholar] [CrossRef]
- Tersoff, J. Chemical Order in Amorphous Silicon Carbide. Phys. Rev. B 1994, 49, 16349–16352. [Google Scholar] [CrossRef]
- Zhou, X.W.; Johnson, R.A.; Wadley, H. Misfit-Energy-Increasing Dislocations in Vapor-Deposited Cofe/Nife Multilayers. Phys. Rev. B 2004, 69, 144113. [Google Scholar] [CrossRef]
- Li, L.; Xia, Z.H.; Curtin, W.A.; Yang, Y.Q. Molecular Dynamics Simulations of Interfacial Sliding in Carbon-Nanotube/Diamond Nanocomposites. J. Am. Ceram. Soc. 2009, 92, 2331–2336. [Google Scholar] [CrossRef]
- Girifalco, L.A.; Hodak, M.; Lee, R.S. Carbon Nanotubes, Buckyballs, Ropes and a Universal Graphitic Potential. Phys. Rev. B 2000, 62, 13104. [Google Scholar] [CrossRef]
- Toghraie, D.; Mokhtari, M.; Afrand, M. Molecular Dynamic Simulation of Copper and Platinum Nanoparticles Poiseuille Flow in a Nanochannels. Phys. E 2016, 84, 152–161. [Google Scholar] [CrossRef]
- Varshney, V.; Patnaik, S.S.; Muratore, C.; Roy, A.K.; Voevodin, A.A.; Farmer, B.L. MD Simulations of Molybdenum Disulphide (MoS2): Force-Field Parameterization and Thermal Transport Behavior. Comput. Mater. Sci. 2010, 48, 101–108. [Google Scholar] [CrossRef]
- Plimpton, S. Fast Parallel Algorithms for Short-Range Molecular Dynamics. J. Comput. Phys. 1995, 117, 1–19. [Google Scholar] [CrossRef]
- Lee, C.; Wei, X.; Kysar, J.W.; Hone, J. Measurement of the Elastic Properties and Intrinsic Strength of Monolayer Graphene. Science 2008, 321, 385–388. [Google Scholar] [CrossRef] [PubMed]
- Komaragiri, U.; Begley, M.R.; Simmonds, J.G. The Mechanical Response of Freestanding Circular Elastic Films Under Point and Pressure Loads. J. Appl. Mech. 2005, 72, 203–212. [Google Scholar] [CrossRef]
- Lovell, M.R.; Khonsari, M.M.; Marangoni, R.D. A Finite Element Analysis of the Frictional Forces Between a Cylindrical Bearing Element and MoS2 Coated and Uncoated Surfaces. Wear 1996, 194, 60–70. [Google Scholar] [CrossRef]
- Castellanos Gomez, A.; Poot, M.; Steele, G.A.; van der Zant, H.S.; Agraït, N.; Rubio Bollinger, G. Elastic Properties of Freely Suspended MoS2 Nanosheets. Adv. Mater. 2012, 24, 772–775. [Google Scholar] [CrossRef] [PubMed]
- Xiong, S.; Cao, G. Molecular Dynamics Simulations of Mechanical Properties of Monolayer MoS2. Nanotechnology 2015, 26, 185705. [Google Scholar] [CrossRef] [PubMed]
- Peña-Álvarez, M.; del Corro, E.; Morales-García, Á.; Kavan, L.; Kalbac, M.; Frank, O. Single Layer Molybdenum Disulfide Under Direct Out-of-Plane Compression: Low-Stress Band-Gap Engineering. Nano Lett. 2015, 15, 3139–3146. [Google Scholar] [CrossRef] [PubMed]
- Lorenz, T.; Joswig, J.; Seifert, G. Stretching and Breaking of Monolayer MoS2—An Atomistic Simulation. 2D Mater. 2014, 1, 011007. [Google Scholar] [CrossRef]





| Pair | C-Mo | C-S | C-Pt | Pt-Mo | Pt-S |
|---|---|---|---|---|---|
| εij (meV) | 48.962 | 13.165 | 38.635 | 661.41 | 177.840 |
| σij (Å) | 3.009 | 3.418 | 2.971 | 2.513 | 2.922 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Y.; Liu, Y.; Ma, T.; Luo, J. Atomic Scale Simulation on the Anti-Pressure and Friction Reduction Mechanisms of MoS2 Monolayer. Materials 2018, 11, 683. https://doi.org/10.3390/ma11050683
Liu Y, Liu Y, Ma T, Luo J. Atomic Scale Simulation on the Anti-Pressure and Friction Reduction Mechanisms of MoS2 Monolayer. Materials. 2018; 11(5):683. https://doi.org/10.3390/ma11050683
Chicago/Turabian StyleLiu, Yang, Yuhong Liu, Tianbao Ma, and Jianbin Luo. 2018. "Atomic Scale Simulation on the Anti-Pressure and Friction Reduction Mechanisms of MoS2 Monolayer" Materials 11, no. 5: 683. https://doi.org/10.3390/ma11050683