Coupling a Chlor-Alkali Membrane Electrolyzer Cell to a Wind Energy Source: Dynamic Modeling and Simulations
Abstract
:1. Introduction
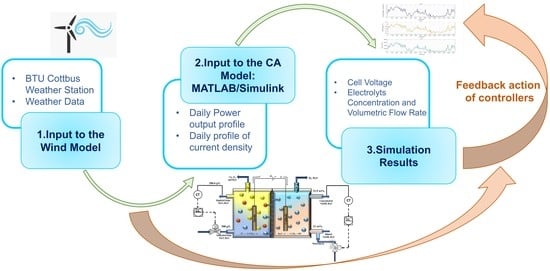
2. Materials and Methods
2.1. Description of the CA Membrane Electrolysis
2.2. Model Development
2.2.1. Mole Balance Model
- Anode Compartment
- Cathode Compartment
2.2.2. Electrochemical Model
- Reversible Voltage
- Activation Overpotential
- Ohmic Overpotential
2.2.3. Controllers
2.3. Input Parameters and Simulation Approach
3. Results and Discussion
3.1. Steady State Simulations
3.2. Dynamic Simulations
3.3. Simulation with Wind Power Profile
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
List of Symbols and Abbreviations
| Abbreviations | |
| CA | Chlor-alkali |
| CEM | Cation exchange membrane |
| CSTR | Continuously stirred tank reactor |
| DAEs | Differential algebraic equations |
| DSA® | Dimensionally stable anode |
| HER | Hydrogen evolution reaction |
| PI | Proportional-integral feedback controller |
| Greek Symbols | |
| Anodic overpotential (V) | |
| Cathodic overpotential (V) | |
| Mean activity coefficient | |
| Faradaic efficiency/Permselectivity (%) | |
| ϱ | |
| Latin Symbols | |
| Thermodynamic potential (V) | |
| Activation overpotential (V) | |
| Total cell voltage (V) | |
| Standard potential (V) | |
| Vapor pressure of pure water (bar) | |
| Saturation pressure (bar) | |
| Transport number of sodium ion | |
| A | Effective area of MEA (m2) |
| b | Parameter in various correlations |
| C | |
| d | Parameter in various correlations |
| e | Parameter in various correlations |
| F | Faraday’s constant (A s mol−1) |
| f | Parameter in various correlations |
| g | Parameter in various correlations |
| i | |
| I | Current (kA) |
| K | Electrical conductivity (Ω−1 cm−1) |
| k | |
| l | Length of resistance (cm) |
| p | Partial pressure (bar) |
| P | Total pressure (bar) |
| R | |
| t | Time |
| T | Cell temperature (°C) |
| V | Volume of cell compartment (L) |
| W | Concentration of electrolyte (wt%) |
| X | |
| y | |
| Superscripts | |
| * | In pure form |
| back | Back transported |
| cons | Consumed |
| in | Inlet flow |
| mem | Membrane |
| out | Outlet flow |
| prod | Produced |
| react | Reacted |
| sat | Saturated |
| Subscripts | |
| act | Activation |
| an | Anode compartment |
| aq | Aqueous |
| cat | Cathode compartment |
| elec | Electrolyte |
| eled | Electrode |
| g | Gaseous |
| L | Liquid |
| (Brine) or sodium chloride solution | |
| (Caustic) or caustic soda solution | |
| ohm | Ohmic |
| OX | Oxidation |
| RED | Reduction |
| rev | Reversible |
References
- Arbeitsgruppe Erneuerbare Energien-Statistik (AGEE-Stat)/Umweltbundesamt. Erneuerbare Energien in Zahlen. November 2021. Available online: https://www.umweltbundesamt.de/themen/klima-energie/erneuerbare-energien/erneuerbare-energien-in-zahlen#uberblick (accessed on 8 December 2021).
- European Commission, Directorate-General for Research and Innovation, Velte D, Kuittinen H. Mission-Oriented R&I Policies: In-Depth Case Studies: Energiewende (Germany): Case Study Report; Publications Office: Bonn, Germany, 2018. [Google Scholar] [CrossRef]
- Hoffmann, C.; Weigert, J.; Esche, E.; Repke, J.-U. Towards demand-side management of the chlor-alkali electrolysis: Dynamic, pressure-driven modeling and model validation of the 1,2-dichloroethane synthesis. Chem. Eng. Sci. 2020, 214, 115358. [Google Scholar] [CrossRef] [Green Version]
- Stadler, I. Power grid balancing of energy systems with high renewable energy penetration by demand response. Util. Policy 2008, 16, 90–98. [Google Scholar] [CrossRef]
- Dehmer, D. The German Energiewende: The First Year. Electr. J. 2013, 26, 71–78. [Google Scholar] [CrossRef]
- Ausfelder, F.; Seitz, A.; von Roon, S. Flexibilitätsoptionen in der Grundstoffindustrie: Methodik, Potenziale, Hemmnisse. July 2018. Available online: https://nbn-resolving.org/html/urn:nbn:de:bsz:wup4-opus-70910 (accessed on 10 March 2020).
- Simkoff, J.M.; Baldea, M. Stochastic Scheduling and Control Using Data-Driven Nonlinear Dynamic Models: Application to Demand Response Operation of a Chlor-Alkali Plant. Ind. Eng. Chem. Res. 2020, 59, 10031–10042. [Google Scholar] [CrossRef]
- Roh, K.; Brée, L.C.; Perrey, K.; Bulan, A.; Mitsos, A. Flexible operation of switchable chlor-alkali electrolysis for demand side management. Appl. Energy 2019, 255, 113880. [Google Scholar] [CrossRef]
- Daryanian, B.; Bohn, R.; Tabors, R. Optimal demand-side response to electricity spot prices for storage-type customers. IEEE Trans. Power Syst. 1989, 4, 897–903. [Google Scholar] [CrossRef]
- Xenos, D.P.; Noor, I.M.; Matloubi, M.; Cicciotti, M.; Haugen, T.; Thornhill, N.F. Demand-side management and optimal operation of industrial electricity consumers: An example of an energy-intensive chemical plant. Appl. Energy 2016, 182, 418–433. [Google Scholar] [CrossRef] [Green Version]
- Kelley, M.; Pattison, R.C.; Baldick, R.; Baldea, M. An MILP framework for optimizing demand response operation of air separation units. Appl. Energy 2018, 222, 951–966. [Google Scholar] [CrossRef]
- Otashu, J.I.; Baldea, M. Demand response-oriented dynamic modeling and operational optimization of membrane-based chlor-alkali plants. Comput. Chem. Eng. 2019, 121, 396–408. [Google Scholar] [CrossRef]
- Brée, L.C.; Perrey, K.; Bulan, A.; Mitsos, A. Demand side management and operational mode switching in chlorine production. AIChE J. 2019, 65, e16352. [Google Scholar] [CrossRef]
- Klaucke, F.; Hoffmann, C.; Hofmann, M.; Tsatsaronis, G. Impact of the chlorine value chain on the demand response potential of the chloralkali process. Appl. Energy 2020, 276, 115366. [Google Scholar] [CrossRef]
- Chlor, E. Questions and Answers on the Chlor-Alkali Sector and the EU Emission Trading System (ETS). Brussels, Belgium. 2010. Available online: http://www.eurochlor.org/media/9379/3-2-questionsandanswersonthechlor-alkalisectorandtheeuemissiontradingsystem.pdf (accessed on 13 August 2020).
- Joint Research Centre, Institute for Prospective Technological Studies; Brinkmann, T.; Giner Santonja, G.; Delgado Sancho, L.; Schorcht, F.; Roudier, S. Best Available Techniques (BAT) Reference Document for the Production of Chlor-Alkali: Industrial Emissions Directive 2010/75/EU (Integrated Pollution Prevention and Control); Publications Office: Bonn, Germany, 2014. [Google Scholar] [CrossRef]
- Schmittinger, P.; Florkiewicz, T.; Curlin, L.C.; Lüke, B.; Scannell, R.; Navin, T.; Zelfel, E.; Bartsch, R. Chlorine, in: Ullmann’s Encyclopedia of Industrial Chemistry; Wiley-VCH Verlag GmbH & Co. KGaA: Weinheim, Germany, 2012. [Google Scholar] [CrossRef]
- Nagy, Z. A Mechanistic Model for the Calculation of Material Balance for a Diaphragm-Type Chlorine Caustic Cell. J. Electrochem. Soc. 1977, 124, 91–95. [Google Scholar] [CrossRef]
- Van Zee, J.; White, R.E. Using Parameter Estimation Techniques with a Simple Model of a Diaphragm-Type Electrolyzer to Predict the Electrical Energy Cost for NaOH Production. J. Electrochem. Soc. 1985, 132, 818–826. [Google Scholar] [CrossRef]
- Van Zee, J.; White, R.E. Simple Models for Diaphragm-Type Chlorine/Caustic Cells: II. Effect of Acidic Anolyte on Steady-State Caustic Yield. J. Electrochem. Soc. 1986, 133, 508–515. [Google Scholar] [CrossRef] [Green Version]
- Van Zee, J.; White, R.E.; Watson, A.T. Simple Models for Diaphragm-Type Chlorine/Caustic Cells: I. Dynamic Behavior. J. Electrochem. Soc. 1986, 133, 501–507. [Google Scholar] [CrossRef]
- Chavan, N.; Pinnow, S.; Polcyn, G.D.; Turek, T. Non-isothermal model for an industrial chlor-alkali cell with oxygen-depolarized cathode. J. Appl. Electrochem. 2015, 45, 899–912. [Google Scholar] [CrossRef]
- Chen, C.-P.; Tilak, B.V. A model for the determination of chloride and chlorate levels in the caustic product of ion-exchange membrane chlor-alkali cells. J. Appl. Electrochem. 1996, 26, 235. [Google Scholar] [CrossRef]
- Chandran, R.; Chin, D.-T. Reactor analysis of a chlor—alkali membrane cell. Electrochimica Acta 1986, 31, 39–50. [Google Scholar] [CrossRef]
- Babu, C.A.; Ashok, S. Peak Load Management in Electrolytic Process Industries. IEEE Trans. Power Syst. 2008, 23, 399–405. [Google Scholar] [CrossRef]
- Richstein, J.C.; Hosseinioun, S.S. Industrial demand response: How network tariffs and regulation (do not) impact flexibility provision in electricity markets and reserves. Appl. Energy 2020, 278, 115431. [Google Scholar] [CrossRef]
- Brée, L.C.; Bulan, A.; Herding, R.; Kuhlmann, J.L.; Mitsos, A.; Perrey, K.; Roh, K. Techno-Economic Comparison of Flexibility Options in Chlorine Production. Ind. Eng. Chem. Res. 2020, 59, 12186–12196. [Google Scholar] [CrossRef]
- Agachi, P.S.; Nagy, Z.K.; Cristea, M.V.; Imre-Lucaci, Á. Model Based Control: Case Studies in Process Engineering; Wiley-VCH Verlag GmbH & Co. KGaA: Weinheim, Germany, 2007. [Google Scholar]
- Budiarto, T.; Esche, E.; Repke, J.; Leksono, E. Dynamic Model of Chloralkali Membrane Process. Procedia Eng. 2017, 170, 473–481. [Google Scholar] [CrossRef]
- Otashu, J.I.; Baldea, M. Scheduling chemical processes for frequency regulation. Appl. Energy 2020, 260, 114125. [Google Scholar] [CrossRef]
- Weigert, J.; Hoffmann, C.; Esche, E.; Fischer, P.; Repke, J.-U. Towards demand-side management of the chlor-alkali electrolysis: Dynamic modeling and model validation. Comput. Chem. Eng. 2021, 149, 107287. [Google Scholar] [CrossRef]
- 32. Dias and Ana Catarina de Bastos Vidal. Chlor-Alkali Membrane Cell Process: Study and Characterization. Ph.D. Thesis, University of Porto, Porto, Portugal, 2010.
- Valderrama, C. Ion-Exchange Membranes in Chlor-Alkali Process. In Encyclopedia of Membranes; Springer: Singapore, 2015; pp. 1–4. [Google Scholar]
- O’Brien, T.F.; Bommaraju, T.V.; Hine, F. Handbook of Chlor-Alkali Technology. In Handbook of Chlor-Alkali Technology; Fundamentals; Springer: New York, NY, USA, 2005; Volume I. [Google Scholar]
- Domga, D.; Domga, R.; Noumi, G.; Tchatchueng, J. Study of Some Electrolysis Parameters for Chlorine and Hydrogen Production Using a New Membrane Electrolyzer. Int. J. Chem. Eng. Anal. Sci. 2017, 2, 1–8. [Google Scholar]
- Jung, J.; Postels, S.; Bardow, A. Cleaner chlorine production using oxygen depolarized cathodes? A life cycle assessment. J. Clean. Prod. 2014, 80, 46–56. [Google Scholar] [CrossRef]
- Paidar, M.; Fateev, V.; Bouzek, K. Membrane electrolysis—History, current status and perspective. Electrochimica Acta 2016, 209, 737–756. [Google Scholar] [CrossRef] [Green Version]
- Mendoza, P.G. Intensification of the Chlor-Alkali Process Using a Rotor-Stator Spinning Disc Membrane Electro-Chemical Reactor. PhD Thesis, Technical University of Eindhoven, Eindhoven, The Netherlands, 2016. Available online: https://research.tue.nl/nl/publications/intensification-of-the-chlor-alkali-process-using-a-rotor-stator- (accessed on 13 August 2020).
- Wellington, T.C. Modern Chlor-Alkali Technology; Elsevier Applied Science: New York, NY, USA, 2012; Volume 5, pp. 93–104. ISBN 1-85166-778-4. [Google Scholar]
- Bergner, D. Reduction of by-product formation in alkali chloride membrane electrolysis. J. Appl. Electrochem. 1990, 20, 716–722. [Google Scholar] [CrossRef]
- Akerlof, G.; Kegeles, G. The Density of Aqueous Solutions of Sodium Hydroxide. J. Am. Chem. Soc. 1939, 61, 1027–1032. [Google Scholar] [CrossRef]
- Twardowski, Z.; Yeager, H.L.; O’Dell, B. A Comparison of Perfluorinated Carboxylate and Sulfonate Ion Exchange Polymers: II. Sorption and Transport Properties in Concentrated Solution Environments. J. Electrochem. Soc. 1982, 129, 328–332. [Google Scholar] [CrossRef]
- Hogendoorn, J.; van der Veen, A.; van der Stegen, J.; Kuipers, H.; Versteeg, G. Application of the Maxwell–Stefan theory to the membrane electrolysis process: Model development and simulations. Comput. Chem. Eng. 2001, 25, 1251–1265. [Google Scholar] [CrossRef]
- Yeo, R.S.; Buck, R.P. Proceedings of the Symposium on Ion Exchange–Transport and Interfacial Properties; The Electrochemical Society: Pennington, NJ, USA, 1981. [Google Scholar]
- Shibli, S.M.A.; Noel, M. Evaluation of transport properties of cation exchange membranes for application in alkali concentrators. J. Appl. Electrochem. 1993, 23, 1147–1150. [Google Scholar] [CrossRef]
- Leah, R.T.; Brandon, N.P.; Vesovic, V.; Kelsall, G.H. Numerical Modeling of the Mass Transport and Chemistry of a Simplified Membrane-Divided Chlor-Alkali Reactor. J. Electrochem. Soc. 2000, 147, 4173. [Google Scholar] [CrossRef]
- Beckmann, R.; Lüke, B. Know-how and technology—improving the return on investment for conversions, expansions and new chlorine plants. Modern Chlor-Alkali Technology. In Proceedings of the 2000 London International Chlorine Symposium Organized by SCI’s Electrochemical Technology Group, London, UK, 31 May–2 June 2000; pp. 196–212. [Google Scholar]
- Ukihashi, H.; Yamabe, M. Perfluorocarboxylate Polymer Membranes. In ACS Symposium Series; American Chemical Society (ACS): Washington, DC, USA, 1982; pp. 427–451. [Google Scholar]
- Pfennig, A.; Schabel, W.; Wolf, H. D5 Properties of Multicomponent Fluid Mixtures. In VDI Heat Atlas; Springer: Singapore, 2010; pp. 513–550. [Google Scholar]
- MacMullin, R.B. Algorithms for the Vapor Pressure of Water Over Aqueous Solutions of Salt and Caustic Soda. J. Electrochem. Soc. 1969, 116, 416–419. [Google Scholar] [CrossRef]
- Sijabat, R.R.; De Groot, M.T.; Moshtarikhah, S.; Van Der Schaaf, J. Maxwell–Stefan model of multicomponent ion transport inside a monolayer Nafion membrane for intensified chlor-alkali electrolysis. J. Appl. Electrochem. 2019, 49, 353–368. [Google Scholar] [CrossRef] [Green Version]
- Adams, J.J.; Bachu, S. Equations of state for basin geofluids: Algorithm review and intercomparison for brines. Geofluids 2002, 2, 257–271. [Google Scholar] [CrossRef]
- Dittman, G.L. Calculation of Brine Properties; Lawrence Livermore National Lab (LLNL): Livermore, CA, USA, February 1977. Available online: https://www.osti.gov/biblio/7111583 (accessed on 13 August 2020).
- Keating, J.T. Modern Chlor-Alkali Technology. J. Membr. Sci. 1996, 115, 109–110. [Google Scholar] [CrossRef]
- Caldwell, D.L. Production of chlorine. In Comprehensive Treatise of Electrochemistry; Springer: Boston, MA, USA, 1981; pp. 105–166. [Google Scholar]
- Bratsch, S.G. Standard Electrode Potentials and Temperature Coefficients in Water at 298.15 K. J. Phys. Chem. Ref. Data 1989, 18, 1–21. [Google Scholar] [CrossRef] [Green Version]
- Suhara, M.; Oda, D. Transport Number through the Perfluorinated Cation Membrane, Flemion. J. Electrochem. Soc. 1980, 127, C407. [Google Scholar]
- Åkerlöf, G. Activity Coefficients of sodium, potassium and lithium chlorides and hydrochloric acid at infinite dilution in water-methyl alcohol mixtures. J. Am. Chem. Soc. 1930, 52, 2353–2368. [Google Scholar] [CrossRef]
- Marangio, F.; Santarelli, M.; Cali, M. Theoretical model and experimental analysis of a high pressure PEM water electrolyser for hydrogen production. Int. J. Hydrogen Energy 2009, 34, 1143–1158. [Google Scholar] [CrossRef]
- Trasatti, S. Progress in the understanding of the mechanism of chlorine evolution at oxide electrodes. Electrochim. Acta 1987, 32, 369–382. [Google Scholar] [CrossRef]
- Moorhouse, J. Modern Chlor-Alkali Technology; John Wiley & Sons: Hoboken, NJ, USA, 2008. [Google Scholar]
- Tilak, B. Chlorine and hydrogen evolution characteristics of ion implanted electrode materials. Mater. Chem. Phys. 1989, 22, 149–161. [Google Scholar] [CrossRef]
- Tilak, B.V.; Chen, C.-P. Generalized analytical expressions for Tafel slope, reaction order and a.c. impedance for the hydrogen evolution reaction (HER): Mechanism of HER on platinum in alkaline media. J. Appl. Electrochem. 1993, 23, 631–640. [Google Scholar] [CrossRef]
- Houda, H. Recent development of Asahi Kasei Chemicals’s IM technology (TSEM 08/358). April 2018. Available online: https://www.eurochlor.org/document/tsem-08-358-recent-development-of-asahi-kasei-chemicalss-im-technology-h-houda/ (accessed on 15 September 2020).
- Campione, A.; Cipollina, A.; Calise, F.; Tamburini, A.; Galluzzo, M.; Micale, G. Coupling electrodialysis desalination with photovoltaic and wind energy systems for energy storage: Dynamic simulations and control strategy. Energy Convers. Manag. 2020, 216, 112940. [Google Scholar] [CrossRef]
- Takahashi, Y.; Obanawa, H.; Noaki, Y. New Electrolyser Design for High Current Density. In Modern Chlor-Alkali Technology; John Wiley & Sons: Hoboken, NJ, USA, 2001; Volume 8, pp. 213–224. [Google Scholar]
- Bergner, D.; Hartmann, M.; Kirsch, H. Voltage-Current Curves: Application to Membrane Cells. In Modern Chlor-Alkali Technology; Springer: Singapore, 1990; pp. 159–170. [Google Scholar]













| Parameter | Value |
|---|---|
| b | 7.95190 |
| d | 1659.793 |
| e | 45.854 |
| Controlled Parameter | Set Point | Manipulated Parameter | Proportional (P) | Integral (I) |
|---|---|---|---|---|
| 0.12 | 0.28 | |||
| 32.5 wt% | 74.27 | 7.42 |
| Parameter | Symbol | Unit | Value | Ref. |
|---|---|---|---|---|
| Inlet temperature of brine | °C | 85 | [34] | |
| Inlet temperature of the caustic solution | °C | 85 | [34] | |
| Inlet volumetric flow rate of the brine | L min−1 | 5 | [11,64] | |
| Inlet volumetric flow rate of the caustic solution | L min−1 | 6 | [12,34] | |
| Inlet density of the brine | g L−1 | 1114 | [34] | |
| Inlet density of the caustic solution | g L−1 | 1299 | [41,51] | |
| Anode and cathode compartment volume per unit cell | L | 100 | [12] | |
| Inlet concentration of NaCl in the brine | g L−1 | 300 | [34] | |
| Inlet concentration of NaOH in the caustic solution | wt% | 31 | [34] | |
| Current density | i | kA m−2 | 3–6 | [34] |
| Water transport number | tH2O | molH2O/molNa+ | 4.1 | [43,44,45] |
| Effective electrode area | A | m2 | 2.7 | [34] |
| Faradaic efficiency/permselectivity | % | 96 | [34] | |
| Reversible voltage | V | 2.1884 | [56] | |
| Exchange current density for the anode | mAcm−2 | 1.2 | [34] | |
| Exchange current density for the cathode | mAcm−2 | 3 | [34] | |
| Tafel slope of anode based) | 0.03 | [60] | ||
| Tafel slope of cathode (Ni coated with Ni–Al) | 0.05 | [62] | ||
| Absolute pressure inside the anode compartment | bar | 1.01 | [34] | |
| Absolute pressure inside the cathode compartment | bar | 1.05 | [34] | |
| Ramping rate | 0.1 | [34] |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Thummar, K.; Abang, R.; Menzel, K.; de Groot, M.T. Coupling a Chlor-Alkali Membrane Electrolyzer Cell to a Wind Energy Source: Dynamic Modeling and Simulations. Energies 2022, 15, 606. https://doi.org/10.3390/en15020606
Thummar K, Abang R, Menzel K, de Groot MT. Coupling a Chlor-Alkali Membrane Electrolyzer Cell to a Wind Energy Source: Dynamic Modeling and Simulations. Energies. 2022; 15(2):606. https://doi.org/10.3390/en15020606
Chicago/Turabian StyleThummar, Krunalkumar, Roger Abang, Katharina Menzel, and Matheus Theodorus de Groot. 2022. "Coupling a Chlor-Alkali Membrane Electrolyzer Cell to a Wind Energy Source: Dynamic Modeling and Simulations" Energies 15, no. 2: 606. https://doi.org/10.3390/en15020606