Influence of Microstepping Signal Shape on Shaft Movement Precision and Torque Variation of the Stepper Motor
Abstract
:1. Introduction
Stepper Motor Principle of Operation
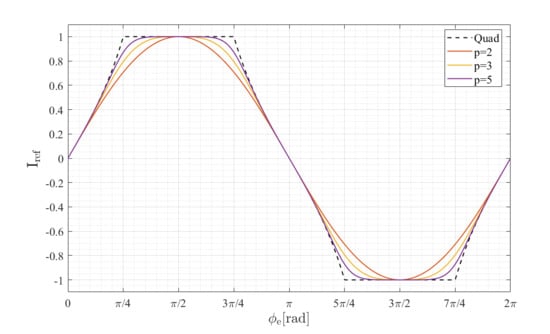
2. Derivation of -Circle Signals
3. Materials and Methods
4. Results
5. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zribi, M.; Chiasson, J. Position control of a PM stepper motor by exact linearization. IEEE Trans. Autom. Control 1991, 36, 620–625. [Google Scholar] [CrossRef]
- Bodson, M.; Chiasson, J.N.; Novotnak, R.T.; Rekowski, R.B. High-performance nonlinear feedback control of a permanent magnet stepper motor. IEEE Trans. Control. Syst. Technol. 1993, 1, 5–14. [Google Scholar] [CrossRef]
- Marino, R.; Peresada, S.; Tomei, P. Nonlinear adaptive control of permanent magnet step motors. Automatica 1995, 31, 1595–1604. [Google Scholar] [CrossRef]
- Shin, D.; Kim, W.; Lee, Y.; Chung, C.C. Phase-Compensated Microstepping for Permanent-Magnet Stepper Motors. IEEE Trans. Ind. Electron. 2013, 60, 5773–5780. [Google Scholar] [CrossRef]
- Anish, N.K.; Krishnan, D.; Moorthi, S.; Selvan, M.P. FPGA based microstepping scheme for stepper motor in Space-Based Solar Power Systems. In Proceedings of the 2012 IEEE 7th International Conference on Industrial and Information Systems (ICIIS), Chennai, India, 6–9 August 2012; pp. 1–5. [Google Scholar] [CrossRef]
- Angadi, S.; Saikumar, V.; Satyanarayana Kumari, B. A novel digital controller for microstepping stepper motor drive using FPGA for Solar Array Drive Assembly in satellites-A comparison With alternative schemes. In Proceedings of the 2013 International Conference on Advances in Computing, Communications and Informatics (ICACCI), Mysore, India, 22–25 August 2013; pp. 1724–1729. [Google Scholar] [CrossRef]
- Richter, W.D. Generalized spherical and simplicial coordinates. J. Math. Anal. Appl. 2007, 336, 1187–1202. [Google Scholar] [CrossRef] [Green Version]
- Khorrami, F.; Krishnamurthy, P.; Melkote, H. Modeling and Adaptive Nonlinear Control of Electric Motors; Springer: Berlin/Heidelberg, Germany, 2003. [Google Scholar]
- Ionică, I.; Modreanu, M.; Morega, A.; Boboc, C. Design and modeling of a hybrid stepper motor. In Proceedings of the 2017 10th International Symposium on Advanced Topics in Electrical Engineering (ATEE), Bucharest, Romania, 23–25 March 2017; pp. 192–195. [Google Scholar] [CrossRef]
- Kim, W.; Shin, D.; Chung, C.C. Microstepping Using a Disturbance Observer and a Variable Structure Controller for Permanent-Magnet Stepper Motors. IEEE Trans. Ind. Electron. 2013, 60, 2689–2699. [Google Scholar] [CrossRef]
- Microstepping of Stepping Motors, The University of Iowa, Department of Computer Science. Available online: http://homepage.divms.uiowa.edu/~jones/step/index.html (accessed on 2 May 2021).
- Wang, C.; Cao, D. New Sensorless Speed Control of a Hybrid Stepper Motor Based on Fuzzy Sliding Mode Observer. Energies 2020, 13, 4939. [Google Scholar] [CrossRef]
- Ganeshanathan, V.; Munasinghe, S.R. High resolution stepper motor controller for tunable laser. In Proceedings of the 2013 IEEE 8th International Conference on Industrial and Information Systems, Peradeniya, Sri Lanka, 17–20 December 2013; pp. 36–41. [Google Scholar] [CrossRef]
- Mukherjee, A.; Karmakar, P.; Kumar Shome, S.; Sen, S.; Datta, U. Precision positioning system for long travel range and submicron resolution. In Proceedings of the 2016 2nd International Conference on Control, Instrumentation, Energy & Communication (CIEC), Kolkata, India, 28–30 January 2016; pp. 83–87. [Google Scholar]
- Szabó, Z.; Bokor, J. L/sup p/norm convergence of rational orthonormal basis function expansions. In Proceedings of the 38th IEEE Conference on Decision and Control (Cat. No.99CH36304), Phoenix, AZ, USA, 7–10 December 1999; Volume 4, pp. 3218–3223. [Google Scholar]
- Data Sheet 6020-1104-01 Rev B MCA1101-xx-3, ACEINNA. Available online: https://www.mouser.com/datasheet/2/940/6020-1104-01_B_Datasheet_2c_Current_Sensor_Fix_Gai-1622847.pdf (accessed on 23 September 2021).
- Data Sheet L-9517-9678-05-A. In VIONIC® Series Encoder System; Renishaw PLC.: Wotton-under-Edge, UK, 2020.
- Jackiewicz, K.; Stras, A.; Ufnalski, B.; Grzesiak, L. Comparative study of two repetitive process control techniques for a grid-tie converter under distorted grid voltage conditions. Int. J. Electr. Power Energy Syst. 2019, 113, 164–175. [Google Scholar] [CrossRef]
- Galecki, A.; Grzesiak, L.; Ufnalski, B.; Kaszewski, A.; Michalczuk, M. Multi-oscillatory current control with anti-windup for grid-connected VSCs operated under distorted grid voltage conditions. In Proceedings of the 2017 19th European Conference on Power Electronics and Applications (EPE’17 ECCE Europe), Warsaw, Poland, 11–14 September 2017; pp. 1–10. [Google Scholar] [CrossRef]
- Kaszewski, A.; Grzesiak, L.; Ufnalski, B. Sterowanie Napędów Elektrycznych, 1st ed.; Wydawnictwo Naukowe PWN: Warsaw, Poland, 2016. [Google Scholar]




























| A | B |
|---|---|
| 0.114 | 0.0581 | 6.67 | 3.09 | 2.16 | 50 |
| spr | |||||
|---|---|---|---|---|---|
| 2.8 | 1.13 | 3.6 | 18.9 | 0.48 | 200 |
| x8 | x16 | x32 |
|---|---|---|
| rpm | rpm | rpm |
| x8 | x16 | x32 |
|---|---|---|
| 552 | 552 | 783 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bednarski, B.; Jackiewicz, K.; Gałecki, A. Influence of Microstepping Signal Shape on Shaft Movement Precision and Torque Variation of the Stepper Motor. Energies 2021, 14, 6107. https://doi.org/10.3390/en14196107
Bednarski B, Jackiewicz K, Gałecki A. Influence of Microstepping Signal Shape on Shaft Movement Precision and Torque Variation of the Stepper Motor. Energies. 2021; 14(19):6107. https://doi.org/10.3390/en14196107
Chicago/Turabian StyleBednarski, Bogdan, Krzysztof Jackiewicz, and Andrzej Gałecki. 2021. "Influence of Microstepping Signal Shape on Shaft Movement Precision and Torque Variation of the Stepper Motor" Energies 14, no. 19: 6107. https://doi.org/10.3390/en14196107