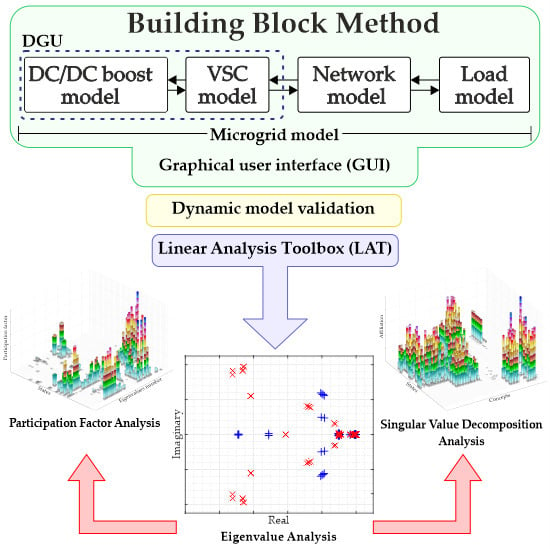
A Building Block Method for Modeling and Small-Signal Stability Analysis of the Autonomous Microgrid Operation
Abstract
:1. Introduction
- The presented modeling approach provides higher flexibility through modularity, less chance for error through a better model overview, and easier microgrid analysis with tested toolboxes compared to traditional state-space matrix obtainment.
- When models are created using the graphical building blocks method, elements in it are connected with other elements in the way to imitate the physical layout of the microgrid; thus, more natural modeling of the complex network configuration with different types of sources and loads is possible.
- More detailed AC/DC and DC/DC converter models than those available in the literature are presented and analyzed as a direct benefit of the proposed modeling approach.
- To support scientific collaboration and microgrid research, MATLAB/Simulink models from this paper, with accompanying documentation, are published on this paper’s MDPI webpage.
2. Autonomous Microgrid Small-Signal State-Space Modeling
- Boost converter subsystem (power model, voltage and current controllers, digital control emulator models);
- VSC subsystem (VSC with LCL filter model, power controller with virtual impedance loop, voltage and current controllers, dead-time, digital control emulator models);
- Network subsystem (a resistive/indictive nature of power lines);
- Load mode subsystem (a resistive/inductive load model).
2.1. State-Space Model of the DC/DC Boost Converter Subsystem
2.1.1. DC/DC Boost Converter Power Model
2.1.2. Voltage and Current Controllers
2.1.3. Digital Control Emulator Model
2.2. State-Space Model of the DC/AC Voltage Source Converter Subsystem
2.2.1. Reference Frame Transformation
2.2.2. Power Controller
2.2.3. Virtual Impedance
2.2.4. VSC Voltage and Current Controllers
2.2.5. Three-Phase Two-Level Three-Wire VSC with Space Vector Modulation and LCL Filter
2.2.6. Digital Control Emulator for VSC
2.3. State-Space Model of the Equivalent Power Line Subsystem
2.4. State-Space Model of the Load Subsystem
3. Proposed Building Block Modeling Method
3.1. State-Space Model Creation
- The converter matrix creation only with an appropriate connection of consisted elements, in a physically logical way. It allows the complex system modeling through the creation of individual control and power stage blocks, and their appropriate graphical connection to form the models of the microgrid subsystems.
- The easy debugging procedure, since the inspection of the variable of interest requires an only connection with a scope, as in any MATLAB/Simulink simulation. Greater clarity and monitoring of the model input/output signals in the blocks reduce the possibility of modeling errors.
- The easy modification of the desired element and with it model complexity. Greater flexibility and modularity of the system modeling is allowed, and also the spent time is significantly reduced. It is possible to easily remove, modify, or insert new blocks of different complexity in a model.
3.2. The Overview of the DGU Model
3.2.1. Boost Converter Subsystem
3.2.2. VSC Subsystem
3.3. Network Subsystem
3.4. Load Subsystem
3.5. A Complete Microgrid Model
- Fast parameter and control structure change, as can be seen from the example of DGU1 showed in Figure 16b.
- An easy selection of the elements and control structure blocks that should be included in the analysis. Model scalability is achieved through the simple selection of the desired elements.
- The switch between the dynamic model and linear model by a simple selection in the GUI. The dynamic model can be compared to the model made of SimPowerSystem components.
3.6. Procedure for Small-Signal Model Analysis
4. Demonstration of the Applied Methodology
4.1. Building Block Model Validation
4.2. Eigenvalue Analysis Using LAT
4.3. Participation Factor Analysis
4.4. Singular Value Decomposition Analysis
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A


References
- Hirsch, A.; Parag, Y.; Guerrero, J. Microgrids: A review of technologies, key drivers, and outstanding issues. Renew. Sustain. Energy Rev. 2018, 90, 402–411. [Google Scholar] [CrossRef]
- Gaur, P.; Singh, S. Investigations on Issues in Microgrids. J. Clean Energy Technol. 2017, 5, 47–51. [Google Scholar] [CrossRef] [Green Version]
- Badal, F.R.; Das, P.; Sarker, S.K.; Das, S.K. A survey on control issues in renewable energy integration and microgrid. Prot. Control Mod. Power Syst. 2019, 4, 8. [Google Scholar] [CrossRef] [Green Version]
- Parhizi, S.; Lotfi, H.; Khodaei, A.; Bahramirad, S. State of the art in research on microgrids: A review. IEEE Access 2015, 3, 890–925. [Google Scholar] [CrossRef]
- Brearley, B.J.; Prabu, R.R. A review on issues and approaches for microgrid protection. Renew. Sustain. Energy Rev. 2017, 67, 988–997. [Google Scholar] [CrossRef]
- Mahmoud, M.S.; Alyazidi, N.M. Pilot-Scale Implementation of Coordinated Control for Autonomous Microgrids. In Microgrid: Advanced Control Methods and Renewable Energy System Integration; Elsevier: Cambridge, MA, USA, 2017; pp. 341–367. ISBN 9780081012628. [Google Scholar]
- Du, W.; Lasseter, R.H.; Khalsa, A.S. Survivability of autonomous microgrid during overload events. IEEE Trans. Smart Grid 2019, 10, 3515–3524. [Google Scholar] [CrossRef]
- Shuai, Z.; Sun, Y.; Shen, Z.J.; Tian, W.; Tu, C.; Li, Y.; Yin, X. Microgrid stability: Classification and a review. Renew. Sustain. Energy Rev. 2016, 58, 167–179. [Google Scholar] [CrossRef]
- Farrokhabadi, M.; Canizares, C.A.; Simpson-Porco, J.W.; Nasr, E.; Fan, L.; Mendoza-Araya, P.; Tonkoski, R.; Tamrakar, U.; Hatziargyriou, N.D.; Lagos, D.; et al. Microgrid Stability Definitions, Analysis, and Examples. IEEE Trans. Power Syst. 2019, 35, 13–29. [Google Scholar] [CrossRef]
- Vadi, S.; Padmanaban, S.; Bayindir, R.; Blaabjerg, F.; Mihet-Popa, L. A review on optimization and control methods used to provide transient stability in microgrids. Energies 2019, 12, 3582. [Google Scholar] [CrossRef] [Green Version]
- Coelho, E.A.A.; Cortizo, P.C.; Garcia, P.F.D. Small-signal stability for parallel-connected inverters in stand-alone ac supply systems. IEEE Trans. Ind. Appl. 2002, 38, 533–542. [Google Scholar] [CrossRef]
- Pogaku, N.; Prodanović, M.; Green, T.C. Modeling, analysis and testing of autonomous operation of an inverter-based microgrid. IEEE Trans. Power Electron. 2007, 22, 613–625. [Google Scholar] [CrossRef] [Green Version]
- Yu, K.; Ai, Q.; Wang, S.; Ni, J.; Lv, T. Analysis and Optimization of Droop Controller for Microgrid System Based on Small-Signal Dynamic Model. IEEE Trans. Smart Grid 2016, 7, 695–705. [Google Scholar] [CrossRef]
- Díaz, G.; González-Morán, C.; Gómez-Aleixandre, J.; Diez, A. Scheduling of droop coefficients for frequency and voltage regulation in isolated microgrids. IEEE Trans. Power Syst. 2010, 25, 489–496. [Google Scholar] [CrossRef]
- Rasheduzzaman, M.; Mueller, J.A.; Kimball, J.W. An accurate small-signal model of inverter-dominated islanded microgrids using (dq) reference frame. IEEE J. Emerg. Sel. Top. Power Electron. 2014, 2, 1070–1080. [Google Scholar] [CrossRef]
- Leitner, S.; Yazdanian, M.; Mehrizi-Sani, A.; Muetze, A. Small-Signal Stability Analysis of an Inverter-Based Microgrid with Internal Model-Based Controllers. IEEE Trans. Smart Grid 2018, 9, 5393–5402. [Google Scholar] [CrossRef]
- Krismanto, A.; Mithulananthan, N.; Lee, K.Y. Comprehensive Modelling and Small Signal Stability Analysis of RES-based Microgrid. IFAC-Pap. 2015, 48, 282–287. [Google Scholar] [CrossRef]
- Tang, X.; Deng, W.; Qi, Z. Investigation of the dynamic stability of microgrid. IEEE Trans. Power Syst. 2014, 29, 698–706. [Google Scholar] [CrossRef]
- Mohammadi, F.D.; Vanashi, H.K.; Feliachi, A. State-Space Modeling, Analysis, and Distributed Secondary Frequency Control of Isolated Microgrids. IEEE Trans. Energy Convers. 2018, 33, 155–165. [Google Scholar] [CrossRef]
- Begum, M.; Li, L.; Zhu, J.; Li, Z. State-Space Modeling and Stability Analysis for Microgrids with Distributed Secondary Control. In Proceedings of the 2018 IEEE 27th International Symposium on Industrial Electronics (ISIE), Cairns, Australia, 13–15 June 2018; pp. 1201–1206. [Google Scholar]
- Wang, Y.; Lu, Z.; Min, Y.; Wang, Z. Small signal analysis of microgrid with multiple micro sources based on reduced order model in islanding operation. In Proceedings of the IEEE Power and Energy Society General Meeting, Detroit, MI, USA, 24–29 July 2011. [Google Scholar]
- Mariani, V.; Vasca, F.; Vásquez, J.C.; Guerrero, J.M. Model Order Reductions for Stability Analysis of Islanded Microgrids with Droop Control. IEEE Trans. Ind. Electron. 2015, 62, 4344–4354. [Google Scholar] [CrossRef] [Green Version]
- Rasheduzzaman, M.; Mueller, J.A.; Kimball, J.W. Reduced-order small-signal model of microgrid systems. IEEE Trans. Sustain. Energy 2015, 6, 1292–1305. [Google Scholar] [CrossRef]
- Taoufik, Q.; Quentin, C.; Li, C.; Xavier Guillaud, F.; Colas; François Gruson, X.K. WP3—Control and Operation of a Grid with 100 % Converter-Based Devices Deliverable 3.2: Local Control and Simulation Tools for Large Transmission Systems; Horizon 2020—LCE-6 project report; Project MIGRATE: Bayreuth, Germany, 2018. [Google Scholar]
- Wang, L.; Guo, X.Q.; Gu, H.R.; Wu, W.Y.; Guerrero, J.M. Precise modeling based on dynamic phasors for droop-controlled parallel-connected inverters. In Proceedings of the IEEE International Symposium on Industrial Electronics, Hangzhou, China, 28–31 May 2012; pp. 475–480. [Google Scholar]
- Mendoza-Araya, P.A.; Venkataramanan, G. Dynamic phasor models for AC Microgrids stability studies. In Proceedings of the 2014 IEEE Energy Conversion Congress and Exposition, ECCE, Pittsburgh, PA, USA, 14–18 September 2014; pp. 3363–3370. [Google Scholar]
- Mariani, V.; Vasca, F.; Guerrero, J.M. Dynamic-phasor-based nonlinear modelling of AC islanded microgrids under droop control. In Proceedings of the 2014 IEEE 11th International Multi-Conference on Systems, Signals and Devices, SSD, Castelldefels-Barcelona, Spain, 11–14 February 2014. [Google Scholar]
- Guo, X.; Lu, Z.; Wang, B.; Sun, X.; Wang, L.; Guerrero, J.M. Dynamic phasors-based modeling and stability analysis of droop-controlled inverters for microgrid applications. IEEE Trans. Smart Grid 2014, 5, 2980–2987. [Google Scholar] [CrossRef] [Green Version]
- Wang, Y.; Wang, X.; Blaabjerg, F.; Chen, Z. Harmonic instability assessment using state-space modeling and participation analysis in inverter-fed power systems. IEEE Trans. Ind. Electron. 2017, 64, 806–816. [Google Scholar] [CrossRef]
- Wang, R.; Sun, Q.; Ma, D.; Liu, Z. The Small-Signal Stability Analysis of the Droop-Controlled Converter in Electromagnetic Timescale. IEEE Trans. Sustain. Energy 2019, 10, 1459–1469. [Google Scholar] [CrossRef]
- Rodriguez-Cabero, A.; Prodanovic, M.; Roldan-Perez, J. Analysis of dynamic properties of VSCs connected to weak grids including the effects of dead time and time delays. IEEE Trans. Sustain. Energy 2019, 10, 1066–1075. [Google Scholar] [CrossRef]
- Modabbernia, M.R.; Sahab, A.R.; Mirzaee, M.T.; Ghorbany, K. The state space average model of boost switching regulator including all of the system uncertainties. Adv. Mater. Res. 2012, 403, 3476–3483. [Google Scholar] [CrossRef]
- Erickson, R.W.; Maksimović, D. Fundamentals of Power Electronics; Kluwer Academic: New York, NY, USA, 2001; pp. 15–27. ISBN 9780792372707. [Google Scholar]
- Corradini, L.; Maksimović, D.; Mattavelli, P.; Zane, R. Digital Control of High-Frequency Switched-Mode Power Converters; John Wiley & Sons: Hoboken, NJ, USA, 2015; pp. 51–70. ISBN 9781119025498. [Google Scholar]
- Franklin, G.F.; Powell, J.D.; Workman, M.L. Digital control of Dynamic Systems; Addison-Wesley: Menlo Park, CA, USA, 1998; pp. 155–180. ISBN 0201820544. [Google Scholar]
- Zhang, X. Modelling and Control of Power Inverters in Microgrids. Ph.D. Thesis, University of Liverpool, Liverpool, UK, 2012. [Google Scholar]
- Agorreta, J.L.; Borrega, M.; López, J.; Marroyo, L. Modeling and control of N-paralleled grid-connected inverters with LCL filter coupled due to grid impedance in PV plants. IEEE Trans. Power Electron. 2011, 26, 770–785. [Google Scholar] [CrossRef]
- Levine, W.S. Control System Fundamentals; CRC Press: Boca Raton, FL, USA, 2010; Chapter 5; pp. 2–32. ISBN 9781420073621. [Google Scholar]
- Hou, X.; Sun, Y.; Yuan, W.; Han, H.; Zhong, C.; Guerrero, J.M. Conventional P-ω/Q-V droop control in highly resistive line of low-voltage converter-based AC microgrid. Energies 2016, 9, 943. [Google Scholar] [CrossRef] [Green Version]
- Rodriguez-Cabero, A.; Roldan-Perez, J.; Prodanovic, M. Virtual Impedance Design Considerations for Virtual Synchronous Machines in Weak Grids. IEEE J. Emerg. Sel. Top. Power Electron. 2019. [Google Scholar] [CrossRef]
- Ahmed, S.; Shen, Z.; Mattavelli, P.; Boroyevich, D.; Karimi, K.J. Small-Signal Model of Voltage Source Inverter (VSI) and Voltage Source Converter (VSC) Considering the DeadTime Effect and Space Vector Modulation Types. IEEE Trans. Power Electron. 2017, 32, 4145–4156. [Google Scholar] [CrossRef]
- Wu, X.; Shen, C. Distributed Optimal Control for Stability Enhancement of Microgrids with Multiple Distributed Generators. IEEE Trans. Power Syst. 2017, 32, 4045–4059. [Google Scholar] [CrossRef]
- Xue, D.; Chen, Y. System Simulation Techniques with MATLAB and Simulink; John Wiley & Sons: Chichester, UK, 2013; pp. 278–280. ISBN 9781118694374. [Google Scholar]
- Pal, B.; Chaudhuri, B. Robust Control in Power Systems; Springer: New York, NY, USA, 2005; pp. 17–19. ISBN 9780387259499. [Google Scholar]
- Leskovec, J.; Rajaraman, A.; Ullman, J.D. Mining of Massive Datasets, 2nd ed.; Cambridge University Press: Cambridge, UK, 2014; pp. 418–422. ISBN 9781107077232. [Google Scholar]






















| STATE-SPACE MICROGRID MODEL I (67 states) | ||
| Blocks | Subsection in paper | Number of states |
| Load in nodes 1,2,3,4,5 and 6 | 2.4 | 12 |
| Network | 2.3 | 10 |
| LCL-filter without dead-time effect and VSC model | 2.2.5 * | 6 per DGU |
| Power controller | 2.2.2 | 3 per DGU |
| Virtual impedance with LPF | 2.2.3 | 2 per DGU |
| VSC current and voltage controllers | 2.2.4 | 4 per DGU |
| STATE-SPACE MICROGRID MODEL II (247 states) | ||
| Additional blocks to MODEL I | Subsection in paper | Number of states |
| LCL-filter with dead-time effect and VSC model | 2.2.5 | 6 per DGU |
| Digital control emulator | 2.2.6 | 42 per DGU |
| Boost converter model | 2.1.1 | 2 per DGU |
| Boost current and voltage controllers | 2.1.2 | 2 per DGU |
| Digital control emulator of boost | 2.2.6 | 14 per DGU |
| * Can be obtained by setting Tdt = 0 in Equations (41) and (42) | ||
| DGU1 = DGU2 = DGU3 | |||
|---|---|---|---|
| Parameter | Value | ||
| Nominal active power Pn | 100 kW | ||
| Nominal phase grid voltage Vn | 230 V | ||
| Nominal grid frequency fg | 50 HZ | ||
| VSC parameters | Value | VSC parameters | Value |
| Switching frequency fsw | 10 kHz | Power coefficient mp | 3.14 × 10−6 |
| Dead time Tdt | 2 μs | Power coefficient nq | 9 × 10−4 |
| Equivalent sampling frequency Ts | 0.5*100 μs | LPF cut-off frequency ωc | 62.8 rad/s |
| Output voltage Vc | 230 V | VC proportional gain Kpu | 0.2475 |
| Filter inductance Li | 163 μH | VC integral gain Kiu | 437.5 |
| Filter resistance Ri | 3 mΩ | CC proportional gain Kpi | 1.4224 |
| Filter capacitance Cf | 70 μF | CC integral gain Kii | 1241.3 |
| Filter damping resistor Rf | 0.21 Ω | Virtual impedance Zvsc1 | (19.6 + j3.9) mΩ |
| Filter inductance Lg | 34 μH | Virtual impedance Zvsc2 | (0 + j0) mΩ |
| Filter resistance Rg | 1 mΩ | Virtual impedance Zvsc3 | (38.7 + j7.8) mΩ |
| Virtual impedance LPF ωc | 62.8 rad/s | ||
| Boost parameters | Value | Boost parameters | Value |
| DC-link voltage Vdc | 800 V | Switching resistance Ronb | 2 mΩ |
| DC-link capacitor Cdc | 10 mF | Diode voltage drop VDb | 1.1 V |
| Input voltage Vinb | 540 V | VC proportional gain Kpub | 11.869 |
| Filter inductance Llb | 300 μH | VC integral gain Kiub | 364.07 |
| Filter resistance Rlb | 1 mΩ | CC proportional gain Kpib | 0.0011 |
| Switching frequency fswb | 10 kHz | CC integral gain Kiib | 1.3229 |
| Grid parameters | Value | Load parameters | Value |
| Line impedance Zl14 | (0.1162 + j0.0233) Ω | Load impedance Zload1 | (7 + j2.198) Ω |
| Line impedance Zl25 | (0.1356 + j0.0271) Ω | Load impedance Zload2 | (14 + j4.396) Ω |
| Line impedance Zl36 | (0.0969 + j0.0194) Ω | Load impedance Zload3 | (4.85 + j1.445) Ω |
| Line impedance Zl45 | (0.0193 + j0.0091) Ω | Load impedance Zload4 | (2.4 + j0.7536) Ω |
| Line impedance Zl56 | (0.0231 + j0.011) Ω | Load impedance Zload5,6 | (1.6 + j0.5024) Ω |
| Steady-state operating points (DGU1 = 1, DGU2 = 2, DGU3 = 3) | |||
|---|---|---|---|
| Parameter | Value | Parameter | Value |
| Iid1, Iid2, Iid3 [A] | [180, 177, 182] | Ilb1,Ilb2 Ilb3 [A] | [148, 148, 148] |
| Iiq1, Iiq2, Iiq3 [A] | [−51, −45, −52] | Db1, Db2, Db3 | [0.326, 0.326, 0.326] |
| Ucd1, Ucd2, Ucd3 [V] | [299, 304, 295] | I14D, I14Q [A] | [141, −42] |
| Ucq1, Ucq2, Ucq3 [V] | [0.5, 0, 1] | I25D, I25Q [A] | [156, −42] |
| Igd1, Igd2, Igd3 [A] | [179, 175, 181] | I36D, I36Q [A] | [127, −40] |
| Igq1, Igq2, Igq3 [A] | [−57, −51, −58] | I45D, I45Q [A] | [34.5, −11] |
| UgD1, UgD2, UgD3 [V] | [296, 302, 292] | I56D, I56Q [A] | [32, −6] |
| UgQ1, UgQ2, UgQ3 [V] | [3, 3, 3] | Iload1D, Iload1Q [A] | [39, −12] |
| δ01, δ02, δ03 [rad] | [0, −3.88 × 10−4, −3.3 × 10−3] | Iload2D, Iload2Q [A] | [19.6, −6] |
| Dd1, Dd2, Dd3 | [0.375, 0.381, 0.37] | Iload3D, Iload3Q [A] | [55, −16] |
| Dq1, Dq2, Dq3 | [0.017, 0.017, 0.017] | Iload4D, Iload4Q [A] | [106, −31] |
| Udc1, Udc2, Udc3, [V] | [800, 800, 800] | Iload5D, Iload5Q [A] | [159, −47] |
| Iload6D, Iload6Q [A] | [158, −47] | ||
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Banković, B.; Filipović, F.; Mitrović, N.; Petronijević, M.; Kostić, V. A Building Block Method for Modeling and Small-Signal Stability Analysis of the Autonomous Microgrid Operation. Energies 2020, 13, 1492. https://doi.org/10.3390/en13061492
Banković B, Filipović F, Mitrović N, Petronijević M, Kostić V. A Building Block Method for Modeling and Small-Signal Stability Analysis of the Autonomous Microgrid Operation. Energies. 2020; 13(6):1492. https://doi.org/10.3390/en13061492
Chicago/Turabian StyleBanković, Bojan, Filip Filipović, Nebojša Mitrović, Milutin Petronijević, and Vojkan Kostić. 2020. "A Building Block Method for Modeling and Small-Signal Stability Analysis of the Autonomous Microgrid Operation" Energies 13, no. 6: 1492. https://doi.org/10.3390/en13061492