The Enhanced Average Model of the Smart Transformer with the Wye-Delta Connection of Dual Active Bridges
Abstract
:1. Introduction
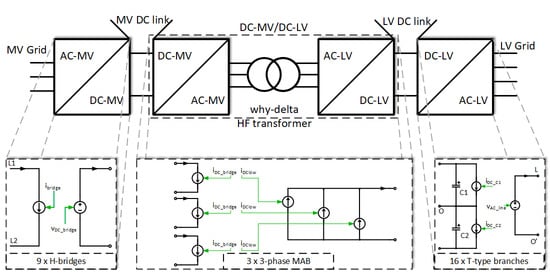
2. Average Model of the ST
2.1. Model of the AC-MV/DC-MV Side of ST
2.2. Model of the Isolated DC-DC Converter with Wye-Delta Transformer
2.3. Model of the DC-LV/AC-LV Side of ST
3. Results
3.1. Study of the AC-MV/DC-MV Side of ST
3.2. Study of the DC-MV/DC-LV Power Stage of ST—the Isolated MAB DC-DC Converter with Wye-Delta Transformer
3.3. Study of the DC-LV/AC-LV Side of ST
3.4. The Complete ST Average Model Analysis
4. Discussion
Author Contributions
Funding
Conflicts of Interest
Appendix A
| Symbol | Description |
| σ | index of the created state-space matrices by the simulation software |
| ϕ | phase shift between high frequency voltages vAC_High and vAC_Low |
| αx | angle of the AC voltage vector of the x H-bridge in CHBC |
| ϕx1, ..x2, ..x3 | phase shift between high frequency voltages vAC_High and vAC_Low for each phase x and module of the MAB in the ST |
| αz* | Referenced voltage vector angle for T-type converters working as a controlled current source |
| ..* | indication of referenced values |
| ..’, ..’’, ..’’’ | indication of H-bridges in each phase of the cascaded H-bridge converter (CHBC) |
| Aσ, Bσ, Cσ, Dσ | state matrix, input matrix, output matrix, direct transition matrix respectively |
| a, b, c, n | phases of the grid voltages and currents in abc reference system |
| D | modulation index |
| D | phase shift ratio for DAB converter |
| dx | modulation index of the x H-bridge in CHBC |
| dz1, ..z_m, ..n1 ..n_m | modulation indexes for T-type converters |
| fs | switching frequency |
| i*MVDC | referenced current value for each H-bridge in Multiple Active Bridge (MAB) from the high voltage side |
| iAC | AC current of the one H-bridge in CHBC |
| iAC_High | AC high frequency current of the transformer primary side in the one Dual Active Bridge (DAB) |
| iAC_Low | AC high frequency current of the transformer secondary side in the one Dual Active Bridge (DAB) |
| iDC | DC current of the one H-bridge in CHBC |
| iDC_High | DC current of the one Dual Active Bridge (DAB) from the high voltage side |
| iDC_Low | DC current of the one Dual Active Bridge (DAB) from the low voltage side |
| iDC_Low_X1 | reference current value for current source of DC-link upper capacitor for phase X, where X indicates A, B, C, N phase |
| iDC_Low_X2 | reference current value for current source of DC-link lower capacitor for phase X, where X indicates A, B, C, N phase |
| iLVAC,n1 | AV current of the T-type converter working as a controlled voltage source in phase n |
| iLVAC,z_m ..n_m | AV current of the T-type converter working as a controlled current source in phase z, where z indicates a, b, c and n is the neutral wire |
| iLVAC,z1 | AV current of the T-type converter working as a controlled voltage source in phase z, where z indicates a, b, c |
| iMVAC,x | AC current of the x H-bridge in CHBC |
| iMVDC,x | DC current of the x H-bridge in CHBC |
| iMVDC,x1 ..2 ..3 | current values of each H-bridge in Multiple Active Bridge (MAB) from the high voltage side |
| iMVgrid | AC current of the connected grid form the ST MV side |
| ipeak_1 | current peak value when the current rises |
| ipeak_2 | current peak value when the current start falling |
| L1, L2, L3, N | Output lines of the LV T-type converter |
| Leq | equivalent leakage inductance referred to the transformer primary side |
| Lp | inductance of the transformer primary winding |
| Ls | inductance of the transformer secondary winding |
| m | transformer turn ratio |
| P | active power |
| pAC | Instantaneous active power from AC side of the one H-bridge in CHBC |
| pDC | active power from DC side of the one H-bridge in CHBC |
| PLVAC,z_m | Average active power of the T-type converter |
| Pz | Total average active power of all T-type converters used in the ST LV side |
| Rc | conduction resistance of the transistor in the DAB converter |
| Req | equivalent resistance referred to the transformer primary side |
| Rp | resistance of the transformer primary winding |
| Rs | resistance of the transformer secondary winding |
| T | high frequency transformer current period |
| Ts | switching period |
| u | input of the dynamic system |
| V*LVAC,z_m | Referenced voltage amplitude in phase z, where z indicates a, b, c |
| vAC | AC voltage of the one H-bridge in CHBC |
| vAC_High | AC high frequency voltage of the transformer primary side in the one Dual Active Bridge (DAB) |
| vAC_Low | AC high frequency voltage of the transformer secondary side in the one Dual Active Bridge (DAB) |
| vConv,x | AC referenced voltage of the x H-bridge in CHBC |
| vDC | DC voltage of the one H-bridge in CHBC |
| vDC_High | DC voltage of the one Dual Active Bridge (DAB) from the high voltage side |
| vDC_Low | DC voltage of the one Dual Active Bridge (DAB) from the low voltage side |
| vDC_Low_1, VC1 | average voltage values across DC-link upper capacitor in T-type converter |
| vDC_Low_2, VC2 | average voltage values across DC-link lower capacitor in T-type converter |
| vLVAC,z_m | AV voltage of the T-type converter working as a controlled current source in phase z, where z indicates a, b, c |
| vLVAC,z1 | AV voltage of the T-type converter working as a controlled voltage source in phase z, where z indicates a, b, c |
| vLVDC | DC voltage of the one Dual Active Bridge (DAB) from the low voltage side |
| vLVDC | DC voltage of the T-type converter |
| vMVAC,x | AC voltage of the x H-bridge in CHBC |
| vMVDC,x | DC voltage of the x H-bridge in CHBC |
| vMVgrid | AC voltage of the connected grid form the ST MV side |
| x, | state-transition matrix of the dynamic system and the derivative of the state-transition matrix respectively |
| y | output of the dynamic system |
References
- Mcmurray, W. Power Converter Circuits Having a High Frequency Link. U.S. Patent 3,517,300, 23 June 1970. [Google Scholar]
- She, X.; Huang, A.Q.; Burgos, R. Review of solid-state transformer technologies and their application in power distribution systems. IEEE J. Emerg. Sel. Top. Power Electron. 2013, 1, 186–198. [Google Scholar] [CrossRef]
- Liserre, M.; Buticchi, G.; Andresen, M.; De Carne, G.; Costa, L.F.; Zou, Z.X. The Smart Transformer: Impact on the Electric Grid and Technology Challenges. IEEE Ind. Electron. Mag. 2016, 10, 46–58. [Google Scholar] [CrossRef] [Green Version]
- Jiang, Y.; Breazeale, L.; Ayyanar, R.; Mao, X. Simplified Solid State Transformer modeling for Real Time Digital Simulator (RTDS). In Proceedings of the 2012 IEEE Energy Conversion Congress and Exposition (ECCE), Raleigh, NC, USA, 15–20 September 2012; pp. 1447–1452. [Google Scholar]
- Milczarek, A.; Malinowski, M. Comparison of Classical and Smart Transformers Impact on MV Distribution Grid. IEEE Trans. Power Deliv. 2019, 35, 1339–1347. [Google Scholar]
- Allende, F.R.; Perez, M.A.; Espinosa, J.R.; Gajowik, T.; Stynski, S.; Malinowski, M. Surveying Solid-State Transformer Structures and Controls: Providing Highly Efficient and Controllable Power Flow in Distribution Grids. IEEE Ind. Electron. Mag. 2020, 14, 56–70. [Google Scholar]
- Rong, J.; Ai, X.; Li, Y.; Ren, D. Research on the structure and control strategy of a novel power electronic transformer for AC/DC hybrid distribution network. Appl. Sci. 2019, 9, 727. [Google Scholar] [CrossRef] [Green Version]
- Abu-Siada, A.; Budiri, J.; Abdou, A.F. Solid state transformers topologies, controllers, and applications: State-of-the-art literature review. Electronics 2018, 7, 298. [Google Scholar] [CrossRef] [Green Version]
- Gajowik, T.; Sobol, C.; Stynski, S.; Malinowski, M. Post-fault operation of hybrid DC-DC converter for Solid-State Transformer. In Proceedings of the IECON 2017—43rd Annual Conference of the IEEE Industrial Electronics Society, Beijing, China, 18 December 2017; pp. 5373–5379. [Google Scholar]
- Martin, S.; Agarwal, R.; Shi, Y.; Li, H. Averaged and Small-Signal Models for Modular Multilevel Converter with Square-wave Modulation. In Proceedings of the 2019 IEEE Electric Ship Technologies Symposium (ESTS), Washington, DC, USA, 14–6 August 2019; pp. 577–582. [Google Scholar]
- Mei, N.; Yin, S.; Wei, Z.; Li, Z.; Yin, T.; Wang, Z. Small-signal Modeling and Stability Analysis of MMC Considering Internal Harmonic Interactions. Dianwang Jishu/Power Syst. Technol. 2019, 43, 4495–4501. [Google Scholar]
- Qin, Y.; Wang, K.; Tan, Z.; Xia, Y.; Chen, Y.; Song, Y. Simulation and Analysis of Multilevel DC Transformer Using Different Dual-Active-Bridge DC-DC Converter Models. In Proceedings of the 2019 IEEE Innovative Smart Grid Technologies—Asia (ISGT Asia), Chengdu, China, 21–24 May 2019; pp. 3914–3919. [Google Scholar]
- Shah, S.S.; Bhattacharya, S. Large & small signal modeling of dual active bridge converter using improved first harmonic approximation. In Proceedings of the 2017 IEEE Applied Power Electronics Conference and Exposition (APEC), Tampa, FL, USA, 26–30 March 2017; pp. 1175–1182. [Google Scholar]
- Schweizer, M.; Kolar, J.W. Design and implementation of a highly efficient three-level T-type converter for low-voltage applications. IEEE Trans. Power Electron. 2013, 28, 899–907. [Google Scholar] [CrossRef]
- Saad, H.; Peralta, J.; Dennetiere, S.; Mahseredjian, J.; Jatskevich, J.; Martinez, J.A.; Davoudi, A.; Saeedifard, M.; Sood, V.; Wang, X.; et al. Dynamic averaged and simplified models for MMC-based HVDC transmission systems. IEEE Trans. Power Deliv. 2013, 28, 1723–1730. [Google Scholar]
- Erickson, R.W.; Maksimović, D. Fundamentals of Power Electronics; Springer: Boston, MA, USA, 2001. [Google Scholar]
- Busarello, T.D.C.; Mortezaei, A.; Paredes, H.K.M.; Al-Durra, A.; Pomilio, J.A.; Simoes, M.G. Simplified Small-Signal Model for Output Voltage Control of Asymmetric Cascaded H-Bridge Multilevel Inverter. IEEE Trans. Power Electron. 2018, 33, 3509–3519. [Google Scholar] [CrossRef] [Green Version]
- Sirisukprasert, S.; Huang, A.Q.; Lai, J.-S. Modeling, analysis and control of cascaded-multilevel converter-based STATCOM. In Proceedings of the 2003 IEEE Power Engineering Society General Meeting (IEEE Cat. No.03CH37491), Toronto, YTO, Canada, 13–17 July 2003; pp. 2561–2568. [Google Scholar]
- Di Capua, G.; Shirsavar, S.A.; Hallworth, M.A.; Femia, N. An enhanced model for small-signal analysis of the phase-shifted full-bridge converter. IEEE Trans. Power Electron. 2015, 30, 1567–1576. [Google Scholar] [CrossRef]
- Perez, M.A.; Ruiz, F.; Espinoza, J.R.; Malinowski, M. Control of Solid State Transformer based on Modular Multilevel Converters with Interconnecting Dual Active Bridges. In Proceedings of the IEEE International Symposium on Industrial Electronics, Vancouver, BC, Canada, 12–14 June 2019; pp. 2343–2348. [Google Scholar]
- Mao, S.; Popovic, J.; Ramabhadran, R.; Ferreira, J.A. Comparative study of half-bridge LCC and LLC resonant DC-DC converters for ultra-wide output power range applications. In Proceedings of the 2015 17th European Conference on Power Electronics and Applications (EPE’15 ECCE-Europe), Geneva, Switzerland, 8–10 September 2015. [Google Scholar]
- Zhang, K.; Shan, Z.; Jatskevich, J. Large- and Small-Signal Average-Value Modeling of Dual-Active-Bridge DC-DC Converter Considering Power Losses. IEEE Trans. Power Electron. 2017, 32, 1964–1974. [Google Scholar] [CrossRef]
- Anthon, A.; Zhang, Z.; Andersen, M.A.E.; Holmes, D.G.; McGrath, B.; Teixeira, C.A. The benefits of SiC mosfets in a T-type inverter for grid-tie applications. IEEE Trans. Power Electron. 2017, 32, 2808–2821. [Google Scholar] [CrossRef] [Green Version]
- Jadon, A.S.; Bansal, P.; Department, A.R.S. Design and Implementation of 3-Phase 3-Level T-type Inverter with Different PWM Techniques. Int. J. Electron. Electr. Comput. Syst. 2016, 5, 15–24. [Google Scholar]
- Rafal, K.; Bobrowska-Rafal, M.; Piasecki, S.; Jasinski, M. Coordinated control of grid-connected three-level NPC converter under distorted grid voltage. In Proceedings of the 2011 IEEE International Symposium on Industrial Electronics, Gdansk, Poland, 27–30 June 2011; pp. 1011–1016. [Google Scholar]
- Dannehl, J.; Wessels, C.; Fuchs, F.W. Limitations of Voltage-Oriented PI Current Control of Grid-Connected PWM Rectifiers with LCL Filters. IEEE Trans. Ind. Electron. 2009, 56, 380–388. [Google Scholar] [CrossRef]
- Malinowski, M.; Kazmierkowski, M.P.; Trzynadlowski, A.M. A comparative study of control techniques for PWM rectifiers in AC adjustable speed drives. Power Electron. IEEE Trans. 2003, 18, 1390–1396. [Google Scholar] [CrossRef]
- Han, Y.; Luo, M.; Zhao, X.; Guerrero, J.M.; Xu, L. Comparative Performance Evaluation of Orthogonal-Signal-Generators-Based Single-Phase PLL Algorithms—A Survey. IEEE Trans. Power Electron. 2016, 31, 3932–3944. [Google Scholar] [CrossRef] [Green Version]
- Mlodzikowski, P.; Milczarek, A.; Stynski, S.; Malinowski, M.; Kouro, S. Control of simplified multilevel AC-DC-AC converter for small power generation systems. In Proceedings of the IECON 2013—39th Annual Conference of the IEEE Industrial Electronics. Societyin, Vienna, Austria, 10–13 November 2013; pp. 5951–5956. [Google Scholar]
- Milczarek, A.; Malinowski, M. Monitoring and Control Algorithms Applied to Small Wind Turbine with Grid-Connected/Stand-Alone Mode of Operation. Prz. Elektrotechniczny 2012, 2, 6–11. [Google Scholar]













| Parameter | Value | Parameter | Value |
|---|---|---|---|
| Operating System | Microsoft Windows 10 Home | Graphic Card | NVIDIA GeForce MX150, with 2 GB GDDR5 VRAM |
| Processor | Intel Core i7-8550U CPU @ 1.8 GHz, 4 cores | Hard Drive Type | SATA 3.0 M.2 SSD 256 GB |
| RAM Memory | 16 GB DDR4 | - | - |
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| AC grid voltage—rms (L-L) (AC-MV side of ST) | 3 × 400 (V) | LV DC link capacitors for DAB model | 3.96 (mF) |
| Rated power | 10 (kVA) | LC DV link reference value | 270 (V) |
| Grid resistance (AC-MV side of ST) | 3 (mΩ) | LV DC link capacitors for T-type converter | 2 × 5.28 (mF) |
| Grid inductance (AC-MV side of ST) | 1 (mH) | LC filter single inductance | 0.5 (mH) |
| AC-MV/DC-MV DC link capacitors | 9 × 1.65 (mF) | LC filter single capacitance | 10 (µF) |
| AC-MV/DC-MV DC link reference values | 9 × 270 (V) | Switching frequency | 100 (kHz) |
| Transformer equivalent leakage inductance | 9 × 10 (µH) | LV side AC voltage reference—rms (L-N) | 3 × 70.71 (V) |
| Transformer equivalent winding resistances | 9 × 10 (mΩ) | - | - |
| Power Stage | Average Model | Switching Model |
|---|---|---|
| AC-MV/DC-MV side of ST | 6.89 s | 100.8 s |
| MAB DC-DC Converter with HF transformer | 12.48 s | 400.9 s |
| DC-LV/AC-LV side of ST | 19.78 s | 723.9 s |
| Whole ST topology | 139.6 s | - |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Milczarek, A.; Michna, M. The Enhanced Average Model of the Smart Transformer with the Wye-Delta Connection of Dual Active Bridges. Energies 2020, 13, 4613. https://doi.org/10.3390/en13184613
Milczarek A, Michna M. The Enhanced Average Model of the Smart Transformer with the Wye-Delta Connection of Dual Active Bridges. Energies. 2020; 13(18):4613. https://doi.org/10.3390/en13184613
Chicago/Turabian StyleMilczarek, Adam, and Mariusz Michna. 2020. "The Enhanced Average Model of the Smart Transformer with the Wye-Delta Connection of Dual Active Bridges" Energies 13, no. 18: 4613. https://doi.org/10.3390/en13184613