Assessing the Performance of Sustainable Development Goals of EU Countries: Hard and Soft Data Integration
Abstract
:1. Introduction
2. Background Literature
- utilization of equations describing relations [22];
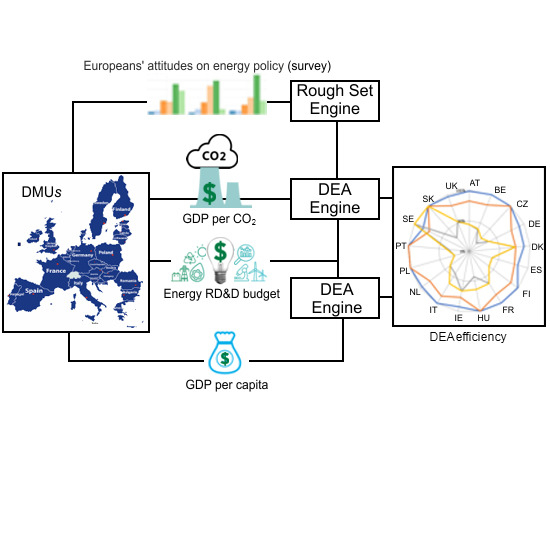
3. Methods
4. Results
4.1. Discussion of Data and Models
4.2. Data Analysis
- SE—the leader, which obtains the high score despite high social awareness and the high GDP per capita;
- FR and IT—with above average GDP per capita and under average agreement;
- RO, BG, and SK—where the score is due to low GDP per capita and low agreement;
- MT—despite a high agreement with average GDP per capita;
- LV—with an average agreement but low GDP per capita.
- with stabile, equal pessimistic, and optimistic results: BG, CY, EL, ES, HR, HU, LT, LV, MT, RO, SE, SI, PT;
- with small, less than 0.2, differences: DE, EE, FR;
- with average, from 0.2 to 0.4, differences: DK, IE, IT, LU, NL, UK;
- with extreme, over 0.4, differences: AT, BE, CZ, FI, PL, SK.
5. Discussion
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| AT | Austria |
| BE | Belgium |
| BG | Bulgaria |
| CY | Cyprus |
| CZ | Czechia |
| DE | Germany |
| DK | Denmark |
| EE | Estonia |
| EL | Greece |
| ES | Spain |
| FI | Finland |
| FR | France |
| HR | Croatia |
| HU | Hungary |
| IE | Ireland |
| IT | Italy |
| LT | Lithuania |
| LV | Latvia |
| LU | Luxembourg |
| MT | Malta |
| NL | The Netherlands |
| PT | Portugal |
| PL | Poland |
| RO | Romania |
| SE | Sweden |
| SI | Slovenia |
| SK | Slovakia |
| UK | United Kingdom |
References
- Mavi, N.K.; Mavi, R.K. Energy and environmental efficiency of OECD countries in the context of the circular economy: Common weight analysis for Malmquist productivity index. J. Environ. Manag. 2019, 247, 651–661. [Google Scholar] [CrossRef]
- Foresight 2020. ISI Emerging Markets Report; ISI Emerging Market Group: London, UK, 2019; Available online: https://info.ceicdata.com/isi-group-foresight-2019-report-download (accessed on 4 April 2020).
- UN General Assembly, Transforming our world: The 2030 Agenda for Sustainable Development, 21 October 2015, A/RES/70/1. Available online: https://www.refworld.org/docid/57b6e3e44.html (accessed on 4 April 2020).
- Siksnelyte, I.; Zavadskas, E.K. Achievements of the European Union Countries in Seeking a Sustainable Electricity Sector. Energies 2019, 12, 2254. [Google Scholar] [CrossRef] [Green Version]
- Malinauskaite, J.; Jouhara, H.; Ahmad, L.; Milani, M.; Montorsi, L.; Venturelli, M. Energy efficiency in industry: EU and national policies in Italy and the UK. Energy 2019, 172, 255–269. [Google Scholar] [CrossRef]
- Lindberg, M.B.; Markard, J.; Andersen, A.D. Policies, actors and sustainability transition pathways: A study of the EU’s energy policy mix. Res. Policy 2019, 48, 103668. [Google Scholar] [CrossRef]
- Nazarko, L.; Melnikas, B. Operationalising Responsible Research and Innovation – tools for enterprises. Eng. Manag. Prod. Serv. 2019, 11, 21–28. [Google Scholar] [CrossRef] [Green Version]
- Nazarko, L. Responsible Research and Innovation in Enterprises: Benefits, Barriers and the Problem of Assessment. J. Open Innov. Technol. Mark. Complex 2020, 6, 12. [Google Scholar] [CrossRef] [Green Version]
- Nazarko, Ł. Future-Oriented Technology Assessment. Proced. Eng. 2017, 182, 504–509. [Google Scholar] [CrossRef]
- International Energy Agency (IEA). Available online: https://www.iea.org (accessed on 4 April 2020).
- Cîrstea, S.; Moldovan-Teselios, C.; Cîrstea, A.; Turcu, A.; Darab, C. Evaluating Renewable Energy Sustainability by Composite Index. Sustainability 2018, 10, 811. [Google Scholar] [CrossRef] [Green Version]
- Momete, D. Measuring Renewable Energy Development in the Eastern Bloc of the European Union. Energies 2017, 10, 2120. [Google Scholar] [CrossRef] [Green Version]
- Arbolino, R.; Boffardi, R.; De Simone, L.; Ioppolo, G. Who achieves the efficiency? A new approach to measure “local energy efficiency.”. Ecol. Ind. 2020, 110, 105875. [Google Scholar] [CrossRef]
- Kaplinski, O.; Peldschus, F.; Nazarko, J.; Kaklauskas, A.; Baušys, R. MCDM, operational research and sustainable development in the trans-border Lithuanian–German– Polish co-operation. Eng. Manag. Prod. Serv. 2019, 11, 7–18. [Google Scholar] [CrossRef] [Green Version]
- Papież, M.; Śmiech, S.; Frodyma, K. Determinants of renewable energy development in the EU countries. A 20-year perspective. Renew. Sustain. Energy Rev. 2018, 91, 918–934. [Google Scholar] [CrossRef]
- Pietrapertosa, F.; Khokhlov, V.; Salvia, M.; Cosmi, C. Climate change adaptation policies and plans: A survey in 11 South East European countries. Renew. Sustain. Energy Rev. 2018, 81, 3041–3050. [Google Scholar] [CrossRef]
- Holma, A.; Leskinen, P.; Myllyviita, T.; Manninen, K.; Sokka, L.; Sinkko, T.; Pasanen, K. Environmental impacts and risks of the national renewable energy targets-A review and a qualitative case study from Finland. Renew. Sustain. Energy Rev. 2018, 82, 1433–1441. [Google Scholar] [CrossRef]
- Neofytou, H.; Karakosta, C.; Gómez, N.C. Impact Assessment of Climate and Energy Policy Scenarios: A Multi-Criteria Approach. In Understanding Risks and Uncertainties in Energy and Climate Policy; Doukas, H., Flamos, A., Lieu, J., Eds.; Springer International Publishing: Cham, Germany, 2019; pp. 123–142. ISBN 978-3-030-03151-0. [Google Scholar]
- Bigerna, S.; Andrea Bollino, C.; Micheli, S. Costs assessments of European environmental policies. Comput. Oper. Res. 2016, 66, 327–335. [Google Scholar] [CrossRef]
- D’Adamo, I.; Rosa, P. Current state of renewable energies performances in the European Union: A new reference framework. Energy Convers. Manag. 2016, 121, 84–92. [Google Scholar] [CrossRef]
- Duscha, V.; Fougeyrollas, A.; Nathani, C.; Pfaff, M.; Ragwitz, M.; Resch, G.; Schade, W.; Breitschopf, B.; Walz, R. Renewable energy deployment in Europe up to 2030 and the aim of a triple dividend. Energy Policy 2016, 95, 314–323. [Google Scholar] [CrossRef]
- DeLlano-Paz, F.; Martínez Fernandez, P.; Soares, I. Addressing 2030 EU policy framework for energy and climate: Cost, risk and energy security issues. Energy 2016, 115, 1347–1360. [Google Scholar] [CrossRef]
- Pacesila, M.; Burcea, S.G.; Colesca, S.E. Analysis of renewable energies in European Union. Renew. Sustain. Energy Rev. 2016, 56, 156–170. [Google Scholar] [CrossRef]
- Cilinskis, E.; Indzere, Z.; Blumberga, D. Prioritization methodology for the determination of national targets. Energy Proced. 2017, 128, 215–221. [Google Scholar] [CrossRef]
- Nikolaev, A.; Konidari, P. Development and assessment of renewable energy policy scenarios by 2030 for Bulgaria. Renew. Energy 2017, 111, 792–802. [Google Scholar] [CrossRef]
- Capros, P.; Kannavou, M.; Evangelopoulou, S.; Petropoulos, A.; Siskos, P.; Tasios, N.; Zazias, G.; DeVita, A. Outlook of the EU energy system up to 2050: The case of scenarios prepared for European Commission’s “clean energy for all Europeans” package using the PRIMES model. Energy Strategy Rev. 2018, 22, 255–263. [Google Scholar] [CrossRef]
- Radulescu, M.; Fedajev, A.; Sinisi, C.; Popescu, C.; Iacob, S. Europe 2020 Implementation as Driver of Economic Performance and Competitiveness. Panel Analysis of CEE Countries. Sustainability 2018, 10, 566. [Google Scholar] [CrossRef] [Green Version]
- Soava, G.; Mehedintu, A.; Sterpu, M.; Raduteanu, M. Impact of Renewable Energy Consumption on Economic Growth: Evidence from European Union Countries. Technol. Econ. Dev. Econ. 2018, 24, 914–932. [Google Scholar] [CrossRef]
- Arbolino, R.; Boffardi, R.; Ioppolo, G. The effectiveness of European energy policy on the Italian system: Regional evidences from a hierarchical cluster analysis approach. Energy Policy 2019, 132, 47–61. [Google Scholar] [CrossRef]
- Bórawski, P.; Bełdycka-Bórawska, A.; Szymańska, E.J.; Jankowski, K.J.; Dubis, B.; Dunn, J.W. Development of renewable energy sources market and biofuels in The European Union. J. Clean. Prod. 2019, 228, 467–484. [Google Scholar] [CrossRef]
- Brożyna, J.; Mentel, G.; Ivanová, E.; Sorokin, G. Classification of Renewable Sources of Electricity in the Context of Sustainable Development of the New EU Member States. Energies 2019, 12, 2271. [Google Scholar] [CrossRef] [Green Version]
- Cirstea, S.D.; Tiron-Tudor, A.; Nistor, R.L.; Cirstea, A.; Fulop, M.T. Renewable Energy and Economic Development ‘Distances’ in Eastern Europe. J. Environ. Prot. Ecol. 2019, 20, 254–264. [Google Scholar]
- Lyeonov, S.; Pimonenko, T.; Bilan, Y.; Štreimikienė, D.; Mentel, G. Assessment of Green Investments’ Impact on Sustainable Development: Linking Gross Domestic Product Per Capita, Greenhouse Gas Emissions and Renewable Energy. Energies 2019, 12, 3891. [Google Scholar] [CrossRef] [Green Version]
- Mikalauskiene, A.; Štreimikis, J.; Mikalauskas, I.; Stankūnienė, G.; Dapkus, R. Comparative Assessment of Climate Change Mitigation Policies in Fuel Combustion Sector of Lithuania and Bulgaria. Energies 2019, 12, 529. [Google Scholar] [CrossRef] [Green Version]
- Pach-Gurgul, A.; Ulbrych, M. Progress of the V4 Countries towards the EU’s Energy and Climate Targets in the Context of Energy Security Improvement. EBER 2019, 7, 175–197. [Google Scholar] [CrossRef]
- Siksnelyte, I.; Zavadskas, E.K.; Bausys, R.; Streimikiene, D. Implementation of EU energy policy priorities in the Baltic Sea Region countries: Sustainability assessment based on neutrosophic MULTIMOORA method. Energy Policy 2019, 125, 90–102. [Google Scholar] [CrossRef] [Green Version]
- Fedajev, A.; Stanujkic, D.; Karabašević, D.; Brauers, W.K.M.; Zavadskas, E.K. Assessment of progress towards “Europe 2020” strategy targets by using the MULTIMOORA method and the Shannon Entropy Index. J. Clean. Prod. 2020, 244, 118895. [Google Scholar] [CrossRef]
- Swain, R.B.; Karimu, A. Renewable electricity and sustainable development goals in the EU. World Dev. 2020, 125, 104693. [Google Scholar] [CrossRef]
- Chodakowska, E.; Nazarko, J. Hybrid Rough Set and Data Envelopment Analysis Approach to Technology Prioritisation. Technol. Econ. Dev. Econ. 2020, 26, 1–22. [Google Scholar] [CrossRef]
- Chodakowska, E.; Nazarko, J. Environmental DEA Method for Assessing Productivity of European Countries. Technol. Econ. Dev. Econ. 2017, 23, 589–607. [Google Scholar] [CrossRef] [Green Version]
- Grochová, L.I.; Myšková, K. How Efficiently are The EU Countries Coping with the Discrepancy Between Economic and Environmental Goals. Soc. Econ. 2016, 38, 319–329. [Google Scholar] [CrossRef]
- Iftikhar, Y.; He, W.; Wang, Z. Energy and CO2 emissions efficiency of major economies: A non-parametric analysis. J. Clean. Prod. 2016, 139, 779–787. [Google Scholar] [CrossRef]
- Madaleno, M.; Moutinho, V.; Robaina, M. Economic and Environmental Assessment: EU Cross-country Efficiency Ranking Analysis. Energy Proced. 2016, 106, 134–154. [Google Scholar] [CrossRef]
- Sanz, T.; Velasco, F.; Yñiguez, R. Is Spain More Efficient Than the Other Countries of EU-28? Searching the Answer through DEA and Malmquist Index. 2016. Available online: http://ceur-ws.org/Vol-1812/JARCA16-paper-7.pdf (accessed on 4 April 2020).
- Moutinho, V.; Madaleno, M.; Robaina, M. The economic and environmental efficiency assessment in EU cross-country: Evidence from DEA and quantile regression approach. Ecol. Ind. 2017, 78, 85–97. [Google Scholar] [CrossRef]
- Gökgöz, F.; Güvercin, M.T. Energy security and renewable energy efficiency in EU. Renew. Sustain. Energy Rev. 2018, 96, 226–239. [Google Scholar] [CrossRef]
- Mezősi, A.; Szabó, L.; Szabó, S. Cost-efficiency benchmarking of European renewable electricity support schemes. Renew. Sustain. Energy Rev. 2018, 98, 217–226. [Google Scholar] [CrossRef]
- Hsieh, J.; Lu, C.; Li, Y.; Chiu, Y.; Xu, Y. Environmental Assessment of European Union Countries. Energies 2019, 12, 295. [Google Scholar] [CrossRef] [Green Version]
- Teng, X.; Lu, L.C.; Chiu, Y.-H. How the European Union reaches the target of CO 2 emissions under the Paris Agreement. Eur. Plan. Stud. 2019, 1–22. [Google Scholar] [CrossRef]
- Zurano-Cervelló, P.; Pozo, C.; Mateo-Sanz, J.M.; Jiménez, L.; Guillén-Gosálbez, G. Sustainability efficiency assessment of the electricity mix of the 28 EU member countries combining data envelopment analysis and optimized projections. Energy Policy 2019, 134, 110921. [Google Scholar] [CrossRef]
- Wernet, G.; Bauer, C.; Steubing, B.; Reinhard, J.; Moreno-Ruiz, E.; Weidema, B. The ecoinvent database version 3 (part I): Overview and methodology. Int. J. Life Cycle Assess. 2016, 21, 1218–1230. [Google Scholar] [CrossRef]
- Banker, R.D.; Charnes, A.; Cooper, W.W. Some Models for Estimating Technical and Scale Inefficiencies in Data Envelopment Analysis. Manag. Sci. 1984, 30, 1078–1092. [Google Scholar] [CrossRef] [Green Version]
- Charnes, A.; Cooper, W.W.; Rhodes, E. Measuring the efficiency of decision making units. Eur. J. Oper. Res. 1978, 2, 429–444. [Google Scholar] [CrossRef]
- A Policy Framework for Climate and Energy in the Period from 2020 to 2030; COM(2014) 15; European Commission: Brussels, Belgium, 2014; Available online: https://eur-lex.europa.eu/legal-content/EN/ALL/?uri=CELEX:52014DC0015 (accessed on 4 April 2020).
- Energy Roadmap 2050. In Brochure; European Commission: Brussels, Belgium, 2012; Available online: https://ec.europa.eu/energy/sites/ener/files/documents/2012_energy_roadmap_2050_en_0.pdf (accessed on 4 April 2020).
- EU Energy 2020—A Strategy for Competitive, Sustainable and Secure Energy; COM(2010) 639; European Commission: Brussels, Belgium, 2010; Available online: http://eur-lex.europa.eu/LexUriServ/LexUriServ.do?uri=COM:2010:0639:FIN:En:PDF (accessed on 4 April 2020).
- Clean Energy for All Europeans—Unlocking Europe’s Growth Potential; European Commission: Brussels, Belgium, 2016; Available online: https://ec.europa.eu/commission/presscorner/detail/en/IP_16_4009 (accessed on 4 April 2020).
- Guidelines on State aid for Environmental Protection and Energy; European Commission: Brussels, Belgium, 2014; Available online: https://eur-lex.europa.eu/legal-content/EN/ALL/?uri=CELEX:52014XC0628(01) (accessed on 4 April 2020).
- Climate Action—Paris Agreement; European Commission: Brussels, Belgium, 2015; Available online: https://ec.europa.eu/clima/policies/international/negotiations/paris_en (accessed on 4 April 2020).
- Climate and Energy Goals for a Competitive, Secure and Low-Carbon EU Economy; European Commission: Brussels, Belgium, 2014; Available online: https://ec.europa.eu/commission/presscorner/detail/en/IP_14_54 (accessed on 4 April 2020).
- European Commission. Energy Strategy and Energy Union. Available online: https://ec.europa.eu/energy/en/topics/energy-strategy-and-energyunion/2030-energy-strategy (accessed on 4 April 2020).
- A Sustainable European Future: The EU Response to the 2030 Agenda for Sustainable Development; Council of the European Union: Brussels, Belgium, 2017; Available online: https://www.consilium.europa.eu/media/23989/st10370-en17.pdf (accessed on 4 April 2020).
- United Nations. The Sustainable Development Goals. Available online: http://www.un.org/sustainabledevelopment/sustainable-development-goals (accessed on 4 April 2020).
- Energy Indicators for Sustainable Development: Guidelines and Methodologies, IAEA, Vienna (2005); International Atomic Energy Agency: Vienna, Austria, 2005; Available online: https://www-pub.iaea.org/MTCD/Publications/PDF/Pub1222_web.pdf (accessed on 4 April 2020).
- Eurostat. Available online: https://ec.europa.eu/eurostat/home? (accessed on 4 April 2020).
- The European Environment Agency (EEA). Available online: https://www.eea.europa.eu (accessed on 4 April 2020).
- Europe 2020 Targets: Statistics and Indicators at EU Level. Available online: https://ec.europa.eu/info/business-economy-euro/economic-and-fiscal-policy-coordination/eu-economic-governance-monitoring-prevention-correction_en (accessed on 4 April 2020).
- The World Bank. Available online: https://www.worldbank.org (accessed on 4 April 2020).
- The World Energy Council. Available online: https://www.worldenergy.org (accessed on 4 April 2020).
- European Investment Bank. Available online: https://www.eib.org/en/index.htm (accessed on 4 April 2020).
- Enerdata, Global Energy Statistical Yearbook. Available online: https://yearbook.enerdata.net (accessed on 4 April 2020).
- IEA (2019), CO2 Emissions from Fuel Combustion. Available online: https://iea.blob.core.windows.net/assets/38460ae3-b53d-4d47-af2a-d6180377e2e0/CO2Highlights2019-Excelfile.XLS (accessed on 4 April 2020).
- Europeans’ Attitudes on EU Energy Policy; Special Eurobarometer 492; Survey conducted by Kantar Belgium at the request of the European Commission, Directorate-General for Energy: Brussels, Belgium, 2019. [CrossRef]
- Cooper, W.W.; Deng, H.; Huang, Z.; Li, S.X. Chance constrained programming approaches to congestion in stochastic data envelopment analysis. Eur. J. Op. Res. 2004, 155, 487–501. [Google Scholar] [CrossRef]
- Agarwal, S. Efficiency Measure by Fuzzy Data Envelopment Analysis Model. Fuzzy Inf. Eng. 2014, 6, 59–70. [Google Scholar] [CrossRef] [Green Version]
- Emrouznejad, A.; Tavana, M.; Hatami-Marbini, A. The State of the Art in Fuzzy Data Envelopment Analysis. In Performance Measurement with Fuzzy Data Envelopment Analysis; Emrouznejad, A., Tavana, M., Eds.; Studies in Fuzziness and Soft Computing; Springer: Berlin/Heidelberg, Germany, 2014; Volume 309, pp. 1–45. ISBN 978-3-642-41371-1. [Google Scholar]
- Kolagar, M.; Hosseini, S.M.H.; Felegari, R.; Fattahi, P. Policy-making for renewable energy sources in search of sustainable development: A hybrid DEA-FBWM approach. Environ. Syst. Decis. 2019, 1–25. [Google Scholar] [CrossRef]
- Zeng, Y.; Guo, W.; Zhang, F. Comprehensive evaluation of renewable energy technical plans based on data envelopment analysis. Energy Proced. 2019, 158, 3583–3588. [Google Scholar] [CrossRef]
- Atanassov, K. Type-1 Fuzzy Sets and Intuitionistic Fuzzy Sets. Algorithms 2017, 10, 106. [Google Scholar] [CrossRef] [Green Version]
- Zimmermann, H.-J. Fuzzy Set Theory—And Its Applications; Springer: Dordrecht, The Netherlands, 2001; ISBN 978-94-010-3870-6. [Google Scholar]
- Chodakowska, E. A Hybrid Approach in Future-Oriented Technology Assessment. In Proceedings of the Future Technologies Conference (FTC) 2019; San Francisco, CA, USA, 14–15 November 2019, Arai, K., Bhatia, R., Kapoor, S., Eds.; Advances in Intelligent Systems and Computing; Springer International Publishing: Cham, Germany, 2020; Volume 1069, pp. 512–525. ISBN 978-3-030-32519-0. [Google Scholar]
- Farrell, M.J. The Measurement of Productive Efficiency. J. R. Stat. Soc. Ser. A 1957, 120, 253. [Google Scholar] [CrossRef]
- Hollingsworth, B.; Smith, P. Use of ratios in data envelopment analysis. Appl. Econ. Lett. 2003, 10, 733–735. [Google Scholar] [CrossRef]
- Hatami-Marbini, A.; Toloo, M. Data envelopment analysis models with ratio data: A revisit. Comput. Ind. Eng. 2019, 133, 331–338. [Google Scholar] [CrossRef]
- Emrouznejad, A.; Amin, G.R. DEA models for ratio data: Convexity consideration. Appl. Math. Model. 2009, 33, 486–498. [Google Scholar] [CrossRef]
- Olesen, O.B.; Petersen, N.C.; Podinovski, V.V. Efficiency measures and computational approaches for data envelopment analysis models with ratio inputs and outputs. Eur. J. Oper. Res. 2017, 261, 640–655. [Google Scholar] [CrossRef] [Green Version]
- Chodakowska, E. Hybrydowy Model Priorytetyzacji Technologii; Oficyna Wydawnicza Politechniki Białostockiej: Białystok, Poland, 2019; ISBN 978-83-65596-90-1. [Google Scholar]
- Pawlak, Z. Rough sets. Int. J. Comput. Inf. Sci. 1982, 11, 341–356. [Google Scholar] [CrossRef]
- Xu, J.; Li, B.; Wu, D. Rough data envelopment analysis and its application to supply chain performance evaluation. Int. J. Prod. Econ. 2009, 122, 628–638. [Google Scholar] [CrossRef]
- Chodakowska, E.; Nazarko, J. Network DEA Models for Evaluating Couriers and Messengers. Proced. Eng. 2017, 182, 106–111. [Google Scholar] [CrossRef]
- Chen, Y.; Zhu, J. Measuring Information Technology’s Indirect Impact on Firm Performance. Inf. Technol. Manag. 2004, 5, 9–22. [Google Scholar] [CrossRef]
- Nazarko, L. Technology Assessment in Construction Sector as a Strategy towards Sustainability. Proced. Eng. 2015, 122, 290–295. [Google Scholar] [CrossRef] [Green Version]
- Ejdys, J.; Halicka, K. Sustainable Adaptation of New Technology—The Case of Humanoids Used for the Care of Older Adults. Sustainability 2018, 10, 3770. [Google Scholar] [CrossRef] [Green Version]








| Author | Methods and Main Indicators | Aims |
|---|---|---|
| Bigerna, Bollino, and Micheli (2016) [19] | Simulation model and general equilibrium model data: GDP, CO2 emission, RES development targets | To construct a model that identifies and estimates potential costs of non-compliance with RES targets in some counties; to present a simulation |
| D’Adamo and Rosa (2016) [20] | Growing steps structure of RE share and average values data: share of RE production and consumption per capita | To assess the EC RES trajectory toward 2020 strategy |
| Duscha, Fougeyrollas, Nathani, Pfaff, Ragwitz, Resch, Schade, Breitschopf, and Walz (2016) [21] | Macroeconomic models: NEMESIS and ASTRA with scenario simulation based on PRIMES data: CO2 reduction, consumption and import of fossil fuels, GDP, employment, RE deployment, costs related to RE deployment | To assess whether RES can positively contribute to the objectives of the European energy policy: combating climate change, improving the security of supply and resulting in economic benefits (job creation and economic growth) |
| deLlano-Paz, Fernandez, and Soares (2016) [22] | Markowitz portfolio theory data: cost and risk of RES technologies (e.g., production costs investment, GHG emissions, plant accident) from other studies | To analyze the EU policy framework goals, cost, risk, and security issues |
| Pacesila, Burcea, and Colesca (2016) [23] | K-means CA data: renewables data (RES share, RES for heating and cooling, transport, energy dependence | To analyze the RE sector in the EU |
| Cilinskis, Indzere, and Blumberga (2017) [24] | TOPSIS data: non-ETS emissions of GHG by different sectors | To introduce a methodology based on multi-criteria analysis TOPSIS to policy planning aimed at climate goals using a Latvian example |
| Momete (2017) [12] | Composite index of RE development based on aggregation data: production and consumption mix: fossil fuels oil, gas, coal, solid fuels, nuclear energy, and RES shares | To investigate the energy development in terms of RE in the Eastern Bloc of the EU |
| Nikolaev and Konidari (2017) [25] | LEAP (Long-range Energy Alternatives Planning) and the MCDM AMS (the combination of three standard MCMs: AHP, MAUT and SMART data: structure of the final energy consumption by fuels, total contribution (capacity, electricity generation) of RES technologies, and policy packages assumptions | To identify the most feasible level of ambition up to 2030 for the Bulgarian RE policy by simulating three scenarios aiming for different RES targets |
| Capros, Kannavou, Evangelopoulou, Petropoulos, Siskos, Tasios, Zazias, and DeVita (2018) [26] | PRIMES model that simulates energy consumption and the energy supply system data: GHG emissions, energy efficiency, RES, energy demand, with costs and required investments | To present a set of scenarios quantified by the PRIMES energy systems model |
| Cîrstea, Moldovan-Teselios, Cîrstea, Turcu, and Darab (2018) [11] | Index construction based on weighting and aggregation data: RE mix shares, indicators from sustainability dimensions of the energy system (environmental, e.g., quality of the natural environment, renewable energy consumption; institutional, e.g., transparency of policymaking; GDP per capita; social, e.g., availability of latest technology, spending on R&D; economic, e.g., production of RE, inflation rate). The index uses other rankings scores. | To design a composite index: RE Sustainability Index and use it to examine European countries |
| Holma, Leskinen, Myllyviita, Manninen, Sokka, Sinkko, and Pasanen (2018) [17] | Qualitative expert judgment methods data: share of energy from RES | To discuss expert assessment of the impacts and risks of RE production in Finland |
| Papież, Śmiech, and Frodyma (2018) [15] | LARS (least angle regression), PCA data: the share of RES in RE mix; indicators from 4 dimensions: environmental, e.g., CO2 emissions per capita; security, e.g., energy import; economic, e.g., GDP per capita, energy consumption per capita and per GDP, cost of energy; political (dummy variables) | To identify factors which determine energy policy in EU countries on the basis on the share of RES in the RE mix |
| Pietrapertosa, Khokhlov, Salvia, and Cosmi (2018) [16] | Preliminary (yes/no) analysis of the existing initiatives data: an overview of the national adaptation policies: National Adaptation Strategy and National Action Plan | To overview adaptation initiatives undertaken in 11 south-east European countries with reference to the policies and measures promoted by the EU National Adaptation Strategy and National Action plan |
| Radulescu, Fedajev, Sinisi, Popescu, and Iacob (2018) [27] | Co-integration tests and OLS panel regression data: Selected Europe 2020 strategy ratios, e.g., GDP, R&D expenses, employment rate, energy consumption, GHG emission etc. | To determine the most important ratios in the “Europe 2020 Strategy” for sustainable and inclusive growth |
| Soava, Mehedintu, Sterpu, and Raduteanu (2018) [28] | Linear regression models, panel data techniques data: GDP, energy consumption from RES | To examine the causal relationship between economic growth and RE consumption |
| Arbolino, Boffardi, and Ioppolo (2019) [29] | Hierarchical CA, convergence analysis panel data model (regression) data: energy consumption shares of energy consumption for different RES and many variables for CA defining levels of R&D, human capital, and demographic features | To propose an approach for ex-post monitoring of the actions implemented in Italian regions |
| Bórawski, Bełdycka-Bórawska, Szymańska, Jankowski, Dubis, and Dunn (2019) [30] | Descriptive statistic and CA data: share of RE in heating cooling and transport | To assess RE market development with regard to biofuels in the EU |
| Brożyna, Mentel, Ivanová, and Sorokin (2019) [31] | Hierarchical CA data: indicators of RE | To distinguish countries among the new EU MSs that increased their electrical capacity from RES |
| Cirstea, Tiron-Tudor, Nistor, Cirstea, and Fulop (2019) [32] | Multidimensional scaling data reduction method and CA data: energy indicators, e.g., energy imports, energy use, energy production, capacity, the share of RES, GHG | To measure the differences between the countries in the Eastern European region in terms of RE and economic development |
| Lindberg and Markard (2019) [6] | Transition pathway (semi-coherent pattern of major changes) analysis data: list of key EU electricity policies and their key industry actors | To assess the EU electricity policy mix supporting different transition pathways |
| Lyeonov, Pimonenko, Bilan, Štreimikienė, and Mentel (2019) [33] | Modified OLS data: GDP per capita and GHG emissions, RE consumption, green investment | To analyze the linkages between GDP per capita, GHG and RE in the total final energy consumption and green investments in the EU |
| Malinauskaite, Jouhara, Ahmad, Milani, Montorsi, and Venturelli (2019) [5] | Descriptive statistics analysis data: energy consumption trends, sources and sectors, energy savings | To review EU strategies and policies on energy efficiency; to present national case studies for Italy and the UK |
| Mikalauskiene, Štreimikis, Mikalauskas, Stankūnienė, and Dapkus (2019) [34] | Descriptive statistics analysis data: GHG emissions and removals by sector, a set of indicators for the assessment of energy intensity, the structure of consumption, dependency, shares of RES in sectors | To assess GHG emission trends and climate change mitigation policies in the fuel combustion sector of Lithuania and Bulgaria |
| Neofytou, Karakosta, and Gómez (2019) [18] | Promethee II data: 12 indicators from 4 dimension: environmental impacts, e.g., GHG reduction, energy-saving; social impact, e.g., employment; economic impacts, e.g., GDP; energy systems impacts, e.g., import, intensity | To assess alternative climate and energy policy scenarios and their socioeconomic, environmental, and energy impacts |
| Pach-Gurgul and Ulbrych (2019) [35] | Hellwig’s multidimensional comparative analysis data: energy consumption, the share of RE in energy consumption | To empirically verify progress made implementing the provisions of the EU Energy Package by the V4 countries |
| Siksnelyte and Zavadskas (2019) [4] | MCDM, TOPSIS data: indicators for monitoring the progress (electricity interconnection, market concentration, electricity prices, retail electricity markets share of RES in final electricity consumption), indicators for the assessment of sustainability: economic (e.g., prices), environmental (e.g., share of RES, distribution losses) security (import) | To monitor the progress of the electricity sector toward EU objectives; assess the sector sustainability |
| Siksnelyte, Zavadskas, Bausys, and Streimikiene (2019) [36] | MCDM MULTIMOORA optimization based on Ratio Analysis technique data: indicators for monitoring the progress of energy import dependency and energy security (e.g., import, supplier concentration), indicators for monitoring the progress of decarbonization (e.g., energy consumption, GHG emission), national energy targets and their implementation, set of EISD indicators to comparative assessment of sustainable: social (e.g., affordability of electricity), economic (e.g., energy use and productivity), and environmental (e.g., GHG emissions) | To present the EU energy policy context; to analyze trends in energy development in eight Baltic Sea Region countries |
| Arbolino, Boffardi, Simone, and Ioppolo (2020) [13] | Efficiency index based on normalization, weighting, and aggregation and PCA data: indicators from dimension: sectoral trends (e.g., GDP, energy intensity per capita, RE production per capita, energy consumption), interaction with the environment (e.g., CO2 emissions), economic and policy aspects (e.g., Tax, R&D Expenditure) | To propose an approach for achieving increased efficiency energy; to present the test on a sample of 20 Italian provinces |
| Fedajev, Stanujkic, Karabašević, Brauers, and Zavadskas (2020) [37] | MCDM MULTIMOORA: The Ratio System, the Reference Point, and the Full Multiplicative Form data: indicators grouped into dimensions: employment, R&D, climate change and energy, education, poverty, and social exclusion: employment rate, GDP expenditure on R&D, GHG, the share of RE, energy consumption per capita, education leavers, attainment of tertiary education, people at risk of poverty | To classify and rank the EU countries according to the progress in the implementation of the EU strategy “Europe 2020” |
| Swain and Karimu (2020) [38] | System of equations based on the OLS model data: electricity price, RE demand, non-RE demand, GDP, heating, and cooling | To examine the RE synergy effect on selected SDGs based on electricity prices in EU countries |
| Authors | DEA Models | Aims | Variables |
|---|---|---|---|
| Grochová and Myšková (2016) [41] | Standard DEA BCC model with slacks | To assess the ability of EU countries to achieve the objectives of Strategy 2020 | Input: electricity production from RES, alternative and nuclear energy, fossil fuel energy, adjusted savings of CO2 damage Output: unemployment, GDP per capita |
| Iftikhar, He, and Wang (2016) [42] | SBM DEA model with an undesirable output | To analyze energy and CO2 emission efficiency (ECEE) of major economies (including the EU) | Input: labor, capital, energy Output: GDP Undesirable output: CO2 |
| Madaleno Moutinho, and Robaina (2016) [43] | Standard CCR and BCC DEA models | To estimate and compare the efficiency | Input: capital, labor, fossil fuel, RE or GDP per labor, GDP per capita, fossil fuel per GDP Output: GDP per GHG |
| Sanz, Yñiguez, and Velasco (2016) [44] | DEA with a desirable and undesirable output and MI | To analyze the efficiency of EU countries, focusing on Spain | Input: gross capital formation (GCF), energy consumption, RE consumption, Output: GDP Undesirable output: GHG |
| Moutinho, Madaleno, and Robaina (2017) [45] | DEA and regression analysis | To estimate the efficiency | Inputs: labor and capital productivity, the weight of fossil energy and the share of RE in GDP Output: GDP per GHG emissions Regression analysis: environmental tax revenues, resources productivity, and domestic material consumption |
| Gökgöz and Güvercin (2018) [46] | super-efficiency DEA and MI | To benchmark the RE performance of countries under different energy regime settings | Input: the deployed renewables Output: an increase in the share of RE in the total electricity generation Undesirable outputs: the imports of coal products, oil products, and natural gas |
| Mezősi, Szabó, and Szabó (2018) [47] | DEA | To assess the cost-efficiency of RE support schemes | Input: cost (efficiency indicator based on support in technology price and electricity consumption), LCOE index (cost level for producing electricity from the RES) Output: the share of assessed RE technology compared to the electricity consumption level (generated electricity/electricity consumption) |
| Hsieh, Lu, Li, Chiu, and Xu (2019) [48] | SBM dynamic DEA | To measure the environmental efficiency of energy | Input: labor, capital, EC (energy consumption) Output: GDP, sulfur oxide SOx, GCF (gross capital formation) |
| Teng, Lu, and Chiu (2019) [49] | DEA type meta-frontier non-radial directional distance function | To evaluate the efficiency of energy and CO2 emission | Input: labor, capital, energy Output: GDP Undesirable output: CO2 |
| Zurano-Cervello, Pozo, Mateo-Sanz, Jimenez, and Guillen-Gosalbez (2019) [50] | Lifecycle and DEA | To assess the sustainability level of the power sector | Input: fossil fuel depletion, total land occupation, water depletion, the annualized cost of electricity Output: climate change (GWP100), human toxicity, ozone depletion, total job-years, electricity generated (data from: [51]) |
| GDP [B US $] | Population [M] | CO2 in [M T] | Total Public Energy RD&D Budget [M US $] | EU Should Encourage Investments in Energy [%] | ||
|---|---|---|---|---|---|---|
| Totally Agree | Tend to and Totally Agree | |||||
| Avg. | 672.39 | 18.30 | 114.62 | 310.80 | 61.18 | 91.18 |
| Std. dev. | 1018.72 | 23.76 | 161.28 | 420.21 | 10.60 | 4.85 |
| GDP | CO2 | |
|---|---|---|
| CO2 | 0.932 | |
| Population | 0.962 | 0.946 |
| GDP per Capita | GDP per CO2 | EU Should Encourage Investments: Totally Agree | |
|---|---|---|---|
| GDP/CO2 | 0.680 | ||
| RD&D budget per capita | 0.593 | 0.443 | |
| EU should encourage investments: | |||
| totally agree | 0.248 1 | 0.433 | |
| tend to agree and totally agree | 0.213 1 | 0.244 1 | 0.646 |
| Country | Ratio DEA only Hard Data | BCC-O | Ratio DEA Model (non-Linear) | Rough BCC DEA Model α = 0.6 | Rough BCC DEA Model α = 0.8 | ||
|---|---|---|---|---|---|---|---|
| AT Austria | 49.1% | 63.6% | 69.8% | 54.0% | 99.7% | 49.7% | 100.0% |
| BE Belgium | 44.9% | 77.3% | 64.0% | 47.7% | 100.0% | 45.6% | 100.0% |
| BG Bulgaria | 100.0% | 100.0% | 100.0% | 100.0% | 100.0% | 100.0% | 100.0% |
| CY Cyprus | 44.4% | 44.9% | 44.4% | 44.9% | 45.4% | 44.9% | 48.8% |
| CZ Czechia | 34.7% | 52.6% | 43.1% | 37.2% | 100.0% | 34.4% | 100.0% |
| DE Germany | 41.2% | 45.3% | 43.8% | 42.0% | 53.9% | 41.9% | 100.0% |
| DK Denmark | 76.0% | 87.0% | 83.9% | 77.7% | 100.0% | 76.0% | 100.0% |
| EE Estonia | 27.9% | 30.8% | 31.0% | 27.6% | 38.7% | 27.6% | 100.0% |
| EL Greece | 56.6% | 56.1% | 56.6% | 56.1% | 56.1% | 56.1% | 62.7% |
| ES Spain | 61.5% | 62.4% | 61.5% | 62.4% | 62.4% | 62.4% | 65.8% |
| FI Finland | 46.5% | 76.9% | 66.9% | 51.0% | 100.0% | 47.2% | 100.0% |
| FR France | 77.1% | 100.0% | 100.0% | 82.5% | 100.0% | 78.6% | 100.0% |
| HR Croatia | 87.9% | 87.6% | 87.9% | 87.6% | 87.6% | 87.6% | 100.0% |
| HU Hungary | 73.5% | 73.3% | 75.6% | 73.3% | 73.3% | 73.3% | 100.0% |
| IE Ireland | 66.3% | 88.8% | 94.9% | 68.5% | 100.0% | 66.3% | 100.0% |
| IT Italy | 63.8% | 100.0% | 82.7% | 69.6% | 100.0% | 65.0% | 100.0% |
| LT Lithuania | 89.3% | 88.7% | 89.3% | 88.7% | 88.7% | 88.7% | 93.1% |
| LU Luxembourg | 48.7% | 63.6% | 67.4% | 51.4% | 79.3% | 48.7% | 100.0% |
| LV Latvia | 63.5% | 99.7% | 100.0% | 99.7% | 99.7% | 99.7% | 100.0% |
| MT Malta | 100.0% | 100.0% | 100.0% | 100.0% | 100.0% | 100.0% | 100.0% |
| NL The Netherlands | 40.7% | 53.8% | 58.1% | 45.6% | 77.8% | 40.9% | 100.0% |
| PL Poland | 43.2% | 58.5% | 56.7% | 43.1% | 100.0% | 43.1% | 100.0% |
| PT Portugal | 67.4% | 74.1% | 76.9% | 66.9% | 73.3% | 66.9% | 100.0% |
| RO Romania | 100.0% | 100.0% | 100.0% | 100.0% | 100.0% | 100.0% | 100.0% |
| SE Sweden | 100.0% | 100.0% | 100.0% | 100.0% | 100.0% | 100.0% | 100.0% |
| SI Slovenia | 50.6% | 50.4% | 50.6% | 50.4% | 50.4% | 50.4% | 54.4% |
| SK Slovakia | 57.0% | 100.0% | 100.0% | 56.8% | 100.0% | 56.4% | 100.0% |
| UK United Kingdom | 64.7% | 74.2% | 77.6% | 67.5% | 98.4% | 66.0% | 100.0% |
| Country | Network Rough BCC DEA Model | |||
|---|---|---|---|---|
| AT Austria | 82.2% | 98.8% | 44.1% | 44.1% |
| BE Belgium | 81.8% | 100.0% | 38.5% | 39.6% |
| CZ Czechia | 100.0% | 100.0% | 17.7% | 28.9% |
| DE Germany | 77.0% | 91.4% | 35.7% | 35.7% |
| DK Denmark | 76.4% | 89.8% | 76.0% | 76.0% |
| ES Spain | 77.0% | 82.7% | 39.4% | 39.4% |
| FI Finland | 85.5% | 99.4% | 40.7% | 40.7% |
| FR France | 83.3% | 99.6% | 62.1% | 62.1% |
| HU Hungary | 100.0% | 100.0% | 42.6% | 63.7% |
| IE Ireland | 76.8% | 92.8% | 66.3% | 66.3% |
| IT Italy | 86.7% | 100.0% | 43.6% | 61.9% |
| NL The Netherlands | 80.8% | 96.7% | 39.3% | 39.3% |
| PL Poland | 100.0% | 100.0% | 25.1% | 25.1% |
| PT Portugal | 100.0% | 100.0% | 34.3% | 36.7% |
| SE Sweden | 72.9% | 84.4% | 100.0% | 100.0% |
| SK Slovakia | 100.0% | 100.0% | 30.1% | 100.0% |
| UK United Kingdom | 80.3% | 95.9% | 51.9% | 51.9% |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chodakowska, E.; Nazarko, J. Assessing the Performance of Sustainable Development Goals of EU Countries: Hard and Soft Data Integration. Energies 2020, 13, 3439. https://doi.org/10.3390/en13133439
Chodakowska E, Nazarko J. Assessing the Performance of Sustainable Development Goals of EU Countries: Hard and Soft Data Integration. Energies. 2020; 13(13):3439. https://doi.org/10.3390/en13133439
Chicago/Turabian StyleChodakowska, Ewa, and Joanicjusz Nazarko. 2020. "Assessing the Performance of Sustainable Development Goals of EU Countries: Hard and Soft Data Integration" Energies 13, no. 13: 3439. https://doi.org/10.3390/en13133439