Effect of Complex Natural Fractures on Economic Well Spacing Optimization in Shale Gas Reservoir with Gas-Water Two-Phase Flow
Abstract
:1. Introduction
2. Methodology
3. Well Spacing Optimization-Field Application
3.1. Reservoir Model
3.2. Simulation Results
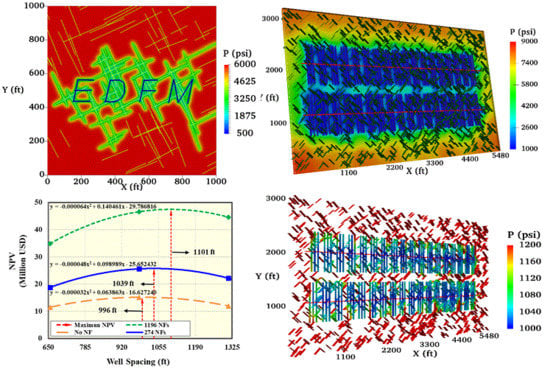
3.3. Visualizations of Pressure Distributions
3.4. Economic Analysis
4. Conclusions
- (1)
- The effect of natural fractures on two shale-gas well performance did not increase linearly with the increasing number of natural fractures. For example, the natural fractures contributed to the incremental gas recovery after 20 years of 22% and 58% for the well spacing of 300 m (984 ft) with a fracture number of 274 and 1196 compared to the no natural fractures case.
- (2)
- The well interference effect was very dominant at a tight, suboptimal well spacing of 200 m (656 ft), as suggested by the straightforward visualizations of matrix/fracture pressure distributions after 20 years. This effect was also posing severe impacts on the economic performance of the well, especially at a larger number of natural fractures and suboptimal designs of well spacing.
- (3)
- A greater well spacing was suggested as optimal when the shale-gas reservoir had a larger number of natural fractures. The relative changes of the optimal spacing for 274 natural fractures case and 1196 natural fractures case, when compared to no natural fractures case, were 4.32% and 10.52%.
- (4)
- Based on maximum NPV estimation, optimal well spacing was technically suggested after appraising multiple scenarios of the number of natural fractures and resolving efficiently myriads of reservoir and fracture uncertainty parameters. However, the company’s final decisions might also consider business financial constraints and objectives out of the scope of this work.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- U.S. Energy Information Administration. Available online: https://www.eia.gov/tools/faqs/faq.php?id=907&t=8 (accessed on 12 March 2020).
- Jacobs, T. To solve frac hits, unconventional engineering must revolve around them. JPT 2019, 27–31. [Google Scholar] [CrossRef]
- Rodriguez, A. Inferences of two dynamic processes on recovery factor and well spacing for shale oil reservoir. In Proceedings of the SPE Liquids-Rich Basins Conference-North America, Odessa, TX, USA, 7–8 November 2019. [Google Scholar] [CrossRef]
- Fiallos Torres, M.X.; Yu, W.; Ganjdanesh, R.; Kerr, E.; Sepehrnoori, K.; Miao, J.; Ambrose, R. Modeling Interwell Interference due to Complex Fracture Hits in Eagle Ford using EDFM. In Proceedings of the International Petroleum Technology Conference, Beijing, China, 26–28 March 2019. [Google Scholar] [CrossRef]
- Morales, A.; Zhang, K.; Gakhar, K.; Marongiu Porcu, M.; Lee, D.; Shan, D.; Malpani, R.; Pope, T.; Sobernheim, D.; Acock, A. Advanced Modeling of Interwell Fracturing Interference: An Eagle Ford Shale Oil Study-Refracturing. In Proceedings of the SPE Hydraulic Fracturing Technology Conference, The Woodlands, TX, USA, 9–11 February 2016. [Google Scholar] [CrossRef]
- Xiong, H.; Liu, S.; Feng, F.; Liu, S.; Yue, K. Optimize Completion Design and Well Spacing with the Latest Complex Fracture Modeling & Reservoir Simulation Technologies—A Permian Basin Case Study with Seven Wells. In Proceedings of the SPE Hydraulic Fracturing Technology Conference, The Woodlands, TX, USA, 5–7 February 2019. [Google Scholar] [CrossRef]
- Tang, J.; Wu, K.; Zuo, L.; Xiao, L.; Sun, S.; Ehlig-Economides, C. Investigation of rupture and slip mechanisms of hydraulic fractures in multiple-layered formations. SPE J. 2019, 24, 2292–2307. [Google Scholar] [CrossRef]
- Xie, J.; Huang, H.; Ma, H.; Zeng, B.; Tang, J.; Yu, W.; Wu, K. Numerical investigation of effect of natural fractures on hydraulic-fracture propagation in unconventional reservoirs. J. Nat. Gas Sci. Eng. 2018, 54, 143–153. [Google Scholar] [CrossRef]
- Tang, J.; Wu, K.; Li, Y.; Hu, X.; Liu, Q.; Ehlig-Economides, C. Numerical investigation of the interactions between hydraulic fracture and bedding planes with non-orthogonal approach angle. Eng. Fract. Mech. 2018, 200, 1–16. [Google Scholar] [CrossRef]
- Balan, H.O.; Gupta, A.; Georgi, D. Optimization of Well and Hydraulic Fracture Spacing for Tight/Shale Gas Reservoirs. In Proceedings of the SPE/AAPG/SEG Unconventional Resources Technology Conference, San Antonio, TX, USA, 1–3 August 2016. [Google Scholar] [CrossRef]
- Chen, Z.; Liao, X.; Zeng, L. Pressure transient analysis in the child well with complex fracture geometries and fracture hits by a semi-analytical model. J. Pet. Eng. 2020, 191, 107–119. [Google Scholar] [CrossRef]
- Liang, Y.; Sheng, J.; Hildebrand, J. Dynamic permeability models in dual-porosity system for unconventional reservoirs: Case studies and sensitivity analysis. In Proceedings of the SPE Reservoir Characterization and Simulation Conference and Exhibition, Abu Dhabi, UAE, 8–10 May 2017. [Google Scholar] [CrossRef]
- Tang, H.; Hasan, R.; Killough, J. Development and application of a fully implicitly coupled wellbore/reservoir simulator to characterize the transient liquid loading in horizontal gas wells. SPE J. 2018, 23, 1615–1629. [Google Scholar] [CrossRef]
- Abivin, P.; Vidma, K.; Xu, T.; Boumessouer, W.; Bailhy, J.; Ejofodomi, E.; Sharma, A.; Menasria, S.; Mikhailov, M. Data Analytics approach to Frac Hit Characterization in Unconventional Plays: Application to Williston Basin. In Proceedings of the International Petroleum Technology Conference, Dhahran, Saudi Arabia, 13–15 January 2020. [Google Scholar] [CrossRef]
- Rahman, M.; Sankaran, S.; Molinari, D.; Yuxing, B. Determination of Stimulated Reservoir Volume SRV during Fracturing. A Data-Driven Approach to Improve Field Operations. In Proceedings of the SPE Hydraulic Fracturing Technology Conference, The Woodlands, TX, USA, 4–6 February 2020. [Google Scholar] [CrossRef]
- McClure, M.; Picone, M.; Fowler, G.; Ratcliff, D.; Kang, C.; Medam, S.; Frantz, J. Nuances and Frequently Asked Questions in Field-Scale Hydraulic Fracture Modeling. In Proceedings of the SPE Hydraulic Fracturing Technology Conference, The Woodlands, TX, USA, 4–6 February 2020. [Google Scholar] [CrossRef]
- Fowler, G.; McClure, M.; Cipolla, C. A Utica Case Study: The Impact of Permeability Estimates on History Matching, Fracture Length, and Well Spacing. In Proceedings of the SPE Annual Technical Conference and Exhibition, Calgary, AB, Canada, 30 September–2 October 2019. [Google Scholar] [CrossRef]
- Morales, A.; Holman, R.; Nugent, D.; Wang, J.; Reece, Z.; Madubuike, C.; Flores, S.; Berndt, T.; Nowaczewski, V.; Cook, S.; et al. Case Study: Optimizing Eagle Ford Field Development through a Fully Integrated Workflow. In Proceedings of the SPE Annual Technical Conference and Exhibition, Calgary, AB, Canada, 30 September–2 October 2019. [Google Scholar] [CrossRef]
- Yu, W.; Sepehrnoori, K. Simulation of gas desorption and geomechanics effects for unconventional gas reservoirs. Fuel 2014, 116, 455–464. [Google Scholar] [CrossRef]
- Yu, W.; Sepehrnoori, K. Shale Gas and Tight Oil Reservoir Simulation, 1st ed.; Elsevier: Cambridge, MA, USA, 2018; ISBN 978-0-12-813868-7. [Google Scholar]
- AITwaijri, M.; Xia, Z.; Yu, W.; Qu, L.; Hu, Y.; Xu, Y.; Sepehrnoori, K. Numerical study of complex fracture geometry effect on two-phase performance of shale-gas wells using the fast EDFM method. J. Pet. Sci. Eng. 2018, 164, 603–622. [Google Scholar] [CrossRef]
- Miao, J.; Yu, W.; Xia, Z.; Zhao, W.; Xu, Y.; Sepehrnoori, K. A simple and fast EDFM method for production simulation in shale reservoirs with complex fracture geometry. In Proceedings of the 2nd International Discrete Fracture Network Engineering Conference, Seattle, WA, USA, 20–22 June 2018. [Google Scholar]
- Dachanuwattana, S.; Jin, J.; Zuloaga-Molero, P.; Li, X.; Xu, Y.; Sepehrnoori, K.; Yu, W.; Miao, J. Application of proxy-based MCMC and EDFM to history match a Vaca Muerta shale oil well. Fuel 2018, 220, 490–502. [Google Scholar] [CrossRef]
- Dachanuwattana, S.; Xia, Z.; Yu, W.; Qu, L.; Wang, P.; Liu, W.; Miao, J.; Sepehrnoori, K. Application of proxy-based MCMC and EDFM to history match a shale gas condensate well. J. Pet. Sci. Eng. 2018, 167, 486–497. [Google Scholar] [CrossRef]
- Yu, W.; Tripoppoom, S.; Sepehrnoori, K.; Miao, J. An automatic history-matching workflow for unconventional reservoirs coupling MCMC and non-intrusive EDFM methods. In Proceedings of the SPE Annual Technical Conference and Exhibition, Dallas, TX, USA, 24–26 September 2018. [Google Scholar] [CrossRef]
- Tripoppoom, S.; Yu, W.; Sepehrnoori, K.; Miao, J. Application of assisted history matching workflow to shale gas well using EDFM and neural network-Markov Chain Monte Carlo algorithm. In Proceedings of the SPE/AAPG/SEG Unconventional Resources Technology Conference, Denver, CO, USA, 22–24 July 2019. [Google Scholar] [CrossRef]
- Xu, Y.; Cavalcante Filho, J.S.A.; Yu, W.; Sepehrnoori, K. Discrete-fracture modeling of complex hydraulic-fracture geometries in reservoir simulators. SPE Reserv. Eval. Eng. 2017, 20, 403–422. [Google Scholar] [CrossRef]
- Xu, Y.; Yu, W.; Sepehrnoori, K. Modeling dynamic behaviors of complex fractures in conventional reservoir simulators. In Proceedings of the SPE/AAPG/SEG Unconventional Resources Technology Conference, Austin, TX, USA, 24–26 July 2017. [Google Scholar] [CrossRef]
- Moinfar, A.; Varavei, A.; Sepehrnoori, K. Development of an efficient embedded discrete fracture model for 3d compositional reservoir simulation in fractured reservoirs. SPE J. 2014, 19, 289–303. [Google Scholar] [CrossRef] [Green Version]
- Xu, Y.; Yu, W.; Li, N.; Lolon, E.; Sepehrnoori, K. Modeling well performance in Piceance Basin Niobrara formation using embedded discrete fracture model. In Proceedings of the SPE/AAPG/SEG Unconventional Resources Technology Conference, Houston, TX, USA, 23–25 July 2018. [Google Scholar] [CrossRef]
- Yu, W.; Miao, J.; Sepehrnoori, K. A revolutionary EDFM method for modeling dynamic behaviors of complex fractures in naturally fractured reservoirs. In Proceedings of the 2nd International Discrete Fracture Network Engineering Conference, Seattle, WA, USA, 20–22 June 2018. [Google Scholar]
- Yu, W.; Xu, Y.; Weijermars, R.; Wu, K.; Sepehrnoori, K. A numerical model for simulating pressure response of well interference and well performance in tight oil reservoirs with complex-fracture geometries using the fast embedded-discrete-fracture-model method. SPE Reserv. Eval. Eng. 2018, 21, 489–502. [Google Scholar] [CrossRef]
- Xu, F.; Yu, W.; Li, X.; Miao, J.; Zhao, G.; Sepehrnoori, K.; Li, X.; Jin, J.; Wen, G. A fast EDFM method for production simulation of complex fractures in naturally fractured reservoirs. In Proceedings of the SPE/AAPG Eastern Regional Meeting, Pittsburgh, PA, USA, 7–11 October 2018. [Google Scholar] [CrossRef]
- Yu, W.; Wu, K.; Zuo, L.; Miao, J.; Sepehrnoori, K. Embedded discrete fracture model assisted study of gas transport mechanisms and drainage area for fractured shale gas reservoirs. In Proceedings of the Unconventional Resources Technology Conference, Denver, CO, USA, 22–24 July 2019. [Google Scholar] [CrossRef]
- Tripoppoom, S.; Xie, J.; Yong, R.; Wu, J.; Yu, W.; Sepehrnoori, K.; Miao, J.; Chang, C.; Li, N. Investigation of different production performances in shale gas wells using assisted history matching: Hydraulic fractures and reservoir characterization from production data. Fuel 2020, 267, 117097. [Google Scholar] [CrossRef]
- Yu, W.; Sepehrnoori, K. Optimization of multiple hydraulically fractured horizontal wells in unconventional gas reservoirs. In Proceedings of the SPE Production and Operations Symposium, Oklahoma City, OK, USA, 23–26 March 2013. [Google Scholar] [CrossRef]


















| Properties | Value | Unit |
|---|---|---|
| Model dimension (x × y × z) | 1670 m × 945 m × 20 m (5480 × 3100 × 65) | m (ft) |
| Number of grid blocks (x × y × z) | 137 × 31 × 1 | - |
| Grid cell size (x × y × z) | 12 m × 30 m × 20 m (40 × 100 × 65) | m (ft) |
| Initial reservoir pressure | 61 (8847) | MPa (psi) |
| Reservoir temperature | 102 (215) | °C (°F) |
| Reservoir depth | 3200 (10499) | m (ft) |
| Matrix water saturation | 0.39 | - |
| Residual water saturation | 20% | - |
| Total compressibility | 4.35 × 10−4 (3 × 10−6) | MPa−1 (psi−1) |
| Reference pressure for compressibility | 0.101 (14.67) | MPa (psi) |
| Total number of clusters | 54 | - |
| Total number of stages | 18 | - |
| Average cluster spacing | 20.4 (67) | m (ft) |
| Stage spacing | 44 (145) | m (ft) |
| Properties | Value | Unit |
|---|---|---|
| Matrix permeability | 455 | nd |
| Hydraulic fracture height | 14.3 (47) | m (ft) |
| Hydraulic fracture half-length | 119.5 (392) | m (ft) |
| Hydraulic fracture conductivity | 50 (164) | md-m (md-ft) |
| Hydraulic fracture water saturation | 0.735 | - |
| Hydraulic fracture width | 0.11 (0.368) | m (ft) |
| Matrix porosity | 6.95 | % |
| Scenario | 20-year Cumulative Gas Production (MMm3/Bcf) | 20-year Cumulative Water Production (tonnes/MSTB) | Relative Change (Gas/Water) (%) |
|---|---|---|---|
| 200 m, no natural fractures | 245.2/8.66 | 3676.8/31.40 | - |
| 200 m, 274 natural fractures | 300.4/10.61 | 4559.7/38.94 | 22/24 |
| 200 m, 1196 natural fractures | 432.7/15.28 | 6162.8/52.63 | 44/35 |
| 300 m, no natural fractures | 279.2/9.86 | 4186.2/35.75 | - |
| 300 m, 274 natural fractures | 364.2/12.86 | 5502.3/46.99 | 30/31 |
| 300 m, 1196 natural fractures | 532.6/18.81 | 7511.7/64.15 | 46/37 |
| 400 m, no natural fractures | 257.1/9.08 | 3928.6/33.55 | - |
| 400 m, 274 natural fractures | 342/12.08 | 5251.8/44.85 | 33/34 |
| 400 m, 1196 natural fractures | 515/18.19 | 7382.9/63.05 | 51/41 |
| Economic Parameters | Value | Unit |
|---|---|---|
| Total well cost | 7.5 | Million dollars |
| Gas price | 1.8 | Dollars per Mscf |
| Unit water disposal cost | 0.5 | Dollars per STB |
| Total tax rate | 12 | % |
| Annual discount rate | 10 | % |
| Scenario | NPV (Million USD) | Interpolated Optimal Well Spacing (m/ft) | Interpolated Maximum NPV (Million USD) |
|---|---|---|---|
| 200 m, no natural fractures | 11.46 | 303.6/996 | 15.15 |
| 300 m, no natural fractures | 15.14 | ||
| 400 m, no natural fractures | 11.92 | ||
| 200 m, 274 natural fractures | 18.77 | 316.7/1039 | 25.73 |
| 300 m, 274 natural fractures | 25.59 | ||
| 400 m, 274 natural fractures | 22.14 | ||
| 200 m, 1312 natural fractures | 34.89 | 335.6/1101 | 47.47 |
| 300 m, 1312 natural fractures | 46.61 | ||
| 400 m, 1312 natural fractures | 44.59 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chang, C.; Li, Y.; Li, X.; Liu, C.; Fiallos-Torres, M.; Yu, W. Effect of Complex Natural Fractures on Economic Well Spacing Optimization in Shale Gas Reservoir with Gas-Water Two-Phase Flow. Energies 2020, 13, 2853. https://doi.org/10.3390/en13112853
Chang C, Li Y, Li X, Liu C, Fiallos-Torres M, Yu W. Effect of Complex Natural Fractures on Economic Well Spacing Optimization in Shale Gas Reservoir with Gas-Water Two-Phase Flow. Energies. 2020; 13(11):2853. https://doi.org/10.3390/en13112853
Chicago/Turabian StyleChang, Cheng, Yongming Li, Xiaoping Li, Chuxi Liu, Mauricio Fiallos-Torres, and Wei Yu. 2020. "Effect of Complex Natural Fractures on Economic Well Spacing Optimization in Shale Gas Reservoir with Gas-Water Two-Phase Flow" Energies 13, no. 11: 2853. https://doi.org/10.3390/en13112853