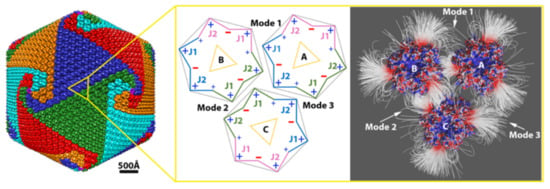
The Roles of Electrostatic Interactions in Capsid Assembly Mechanisms of Giant Viruses
Abstract
:1. Introduction
2. Results and Discussion
2.1. Electrostatic Potential for the Capsomers
2.1.1. Single Capsomer
2.1.2. Interaction between Capsomers
2.1.3. Salt Bridges Contribute to the Electrostatic Interaction between Capsomers
2.2. Electrostatic Binding Force between Capsomers
2.3. Binding Energy Calculation Results from Molecular Mechanics with Poisson–Boltzmann and Surface Area Solvation (MM/PBSA) Analyses
2.4. T-Number and Total Contribution of Each Mode in the Virion of Giant Viruses
3. Methods
3.1. Capsid Structure Preparation
3.2. DelPhi Calculations of Electrostatic Potential
3.3. Capsomer Manipulations to Simulate Capsid Assembly
3.4. Electrostatic Binding Forces between Capsomers
3.5. Molecular Dynamic (MD) Simulations for Capsomer Pairs
3.6. Binding Energy Calculations Using MM/PBSA
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgement
Conflicts of Interest
References
- Xiao, C.; Rossmann, M.G. Structures of giant icosahedral eukaryotic dsDNA viruses. Curr. Opin. Virol. 2011, 1, 101–109. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhang, X.; Xiang, Y.; Dunigan, D.D.; Klose, T.; Chipman, P.R.; van Etten, J.L.; Rossmann, M.G. Three-dimensional structure and function of the Paramecium bursaria chlorella virus capsid. Proc. Natl. Acad. Sci. USA 2011, 108, 14837–14842. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Cherrier, M.V.; Kostyuchenko, V.A.; Xiao, C.; Bowman, V.D.; Battisti, A.J.; Yan, X.; Chipman, P.R.; Baker, T.S.; van Etten, J.L.; Rossmann, M.G. An icosahedral algal virus has a complex unique vertex decorated by a spike. Proc. Natl. Acad. Sci. USA 2009, 106, 11085–11089. [Google Scholar] [CrossRef] [Green Version]
- Yan, X.; Yu, Z.; Zhang, P.; Battisti, A.J.; Holdaway, H.A.; Chipman, P.R.; Bajaj, C.; Bergoin, M.; Rossmann, M.G.; Baker, T.S. The capsid proteins of a large, icosahedral dsDNA virus. J. Mol. Biol. 2009, 385, 1287–1299. [Google Scholar] [CrossRef]
- Yan, X.; Chipman, P.R.; Castberg, T.; Bratbak, G.; Baker, T.S. The marine algal virus PpV01 has an icosahedral capsid with T = 219 quasisymmetry. J. Virol. 2005, 79, 9236–9243. [Google Scholar] [CrossRef]
- Xiao, C.; Kuznetsov, Y.G.; Sun, S.; Hafenstein, S.L.; Kostyuchenko, V.A.; Chipman, P.R.; Suzan-Monti, M.; Raoult, D.; McPherson, A.; Rossmann, M.G. Structural studies of the giant mimivirus. PLoS Biol. 2009, 7, e1000092. [Google Scholar] [CrossRef]
- Arslan, D.; Legendre, M.; Seltzer, V.; Abergel, C.; Claverie, J.M. Distant Mimivirus relative with a larger genome highlights the fundamental features of Megaviridae. Proc. Natl. Acad. Sci. USA 2011, 108, 17486–17491. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Xiao, C.; Fischer, M.G.; Bolotaulo, D.M.; Ulloa-Rondeau, N.; Avila, G.A.; Suttle, C.A. Cryo-EM reconstruction of the Cafeteria roenbergensis virus capsid suggests novel assembly pathway for giant viruses. Sci. Rep. 2017, 7, 5484. [Google Scholar] [CrossRef] [Green Version]
- Klose, T.; Reteno, D.G.; Benamar, S.; Hollerbach, A.; Colson, P.; la Scola, B.; Rossmann, M.G. Structure of faustovirus, a large dsDNA virus. Proc. Natl. Acad. Sci. USA 2016, 113, 6206–6211. [Google Scholar] [CrossRef]
- Schrad, J.R.; Young, E.J.; Abrahao, J.S.; Cortines, J.R.; Parent, K.N. Microscopic Characterization of the Brazilian Giant Samba Virus. Viruses 2017, 9, 30. [Google Scholar] [CrossRef]
- Legendre, M.; Bartoli, J.; Shmakova, L.; Jeudy, S.; Labadie, K.; Adrait, A.; Lescot, M.; Poirot, O.; Bertaux, L.; Bruley, C.; et al. Thirty-thousand-year-old distant relative of giant icosahedral DNA viruses with a pandoravirus morphology. Proc. Natl. Acad. Sci. USA 2014, 111, 4274–4279. [Google Scholar] [CrossRef]
- Claverie, J.M.; Ogata, H. Ten good reasons not to exclude giruses from the evolutionary picture. Nat. Rev. Microbiol. 2009, 7, 615. [Google Scholar] [CrossRef]
- Moreira, D.; Lopez-Garcia, P. Ten reasons to exclude viruses from the tree of life. Nat. Rev. Microbiol. 2009, 7, 306–311. [Google Scholar] [CrossRef]
- Raoult, D.; Forterre, P. Redefining viruses: Lessons from Mimivirus. Nat. Rev. Microbiol. 2008, 6, 315–319. [Google Scholar] [CrossRef]
- Rossmann, M.G.; Johnson, J.E. Icosahedral RNA virus structure. Annu. Rev. Biochem. 1989, 58, 533–573. [Google Scholar] [CrossRef]
- Benson, S.D.; Bamford, J.K.; Bamford, D.H.; Burnett, R.M. Does common architecture reveal a viral lineage spanning all three domains of life? Mol. Cell 2004, 16, 673–685. [Google Scholar] [CrossRef]
- Wrigley, N.G. An electron microscope study of the structure of Sericesthis iridescent virus. J. Gen. Virol. 1969, 5, 123–134. [Google Scholar] [CrossRef]
- Yan, X.; Olson, N.H.; Van Etten, J.L.; Bergoin, M.; Rossmann, M.G.; Baker, T.S. Structure and assembly of large lipid-containing dsDNA viruses. Nat. Struct. Biol. 2000, 7, 101–103. [Google Scholar] [Green Version]
- Suarez, C.; Welsch, S.; Chlanda, P.; Hagen, W.; Hoppe, S.; Kolovou, A.; Pagnier, I.; Raoult, D.; Krijnse Locker, J. Open membranes are the precursors for assembly of large DNA viruses. Cell Microbiol. 2013, 15, 1883–1895. [Google Scholar] [CrossRef] [Green Version]
- Fang, Q.; Zhu, D.; Agarkova, I.; Adhikari, J.; Klose, T.; Liu, Y.; Chen, Z.; Sun, Y.; Gross, M.L.; van Etten, J.L; et al. Near-atomic structure of a giant virus. Nat. Commun. 2019, 10, 388. [Google Scholar] [CrossRef]
- Zhao, G.; Perilla, J.R.; Yufenyuy, E.L.; Meng, X.; Chen, B.; Ning, J.; Ahn, J.; Gronenborn, A.M.; Schulten, K.; Aiken, C.; et al. Mature HIV-1 capsid structure by cryo-electron microscopy and all-atom molecular dynamics. Nature 2013, 497, 643–646. [Google Scholar] [CrossRef] [Green Version]
- Hagan, M.F.; Zandi, R. Recent advances in coarse-grained modeling of virus assembly. Curr. Opin. Virol. 2016, 18, 36–43. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Roos, W.H.; Gibbons, M.M.; Arkhipov, A.; Uetrecht, C.; Watts, N.R.; Wingfield, P.T.; Steven, A.C.; Heck, A.J.; Schulten, K.; Klug, W.S.; et al. Squeezing protein shells: How continuum elastic models, molecular dynamics simulations, and experiments coalesce at the nanoscale. Biophys. J. 2010, 99, 1175–1181. [Google Scholar] [CrossRef]
- Arkhipov, A.; Freddolino, P.L.; Schulten, K. Stability and dynamics of virus capsids described by coarse-grained modeling. Structure 2006, 14, 1767–1777. [Google Scholar] [CrossRef]
- Hagan, M.F. Modeling Viral Capsid Assembly. Adv. Chem. Phys. 2014, 155, 1–68. [Google Scholar] [Green Version]
- Koehl, P. Large Eigenvalue Problems in Coarse-Grained Dynamic Analyses of Supramolecular Systems. J. Chem. Theory Comput. 2018, 14, 3903–3919. [Google Scholar] [CrossRef]
- Freddolino, P.L.; Arkhipov, A.S.; Larson, S.B.; McPherson, A.; Schulten, K. Molecular dynamics simulations of the complete satellite tobacco mosaic virus. Structure 2006, 14, 437–449. [Google Scholar] [CrossRef]
- Jiang, J.; Yang, J.; Sereda, Y.V.; Ortoleva, P.J. Early stage P22 viral capsid self-assembly mediated by scaffolding protein: Atom-resolved model and molecular dynamics simulation. J. Phys. Chem. B 2015, 119, 5156–5162. [Google Scholar] [CrossRef]
- Li, L.; Jia, Z.; Peng, Y.; Godar, S.; Getov, I.; Teng, S.; Alper, J.; Alexov, E. Forces and Disease: Electrostatic force differences caused by mutations in kinesin motor domains can distinguish between disease-causing and non-disease-causing mutations. Sci. Rep. 2017, 7, 8237. [Google Scholar] [CrossRef]
- Siber, A.; Podgornik, R. Role of electrostatic interactions in the assembly of empty spherical viral capsids. Phys. Rev. E Stat. Nonlinear Soft Matter Phys. 2007, 76, 061906. [Google Scholar] [CrossRef] [Green Version]
- van der Schoot, P.; Bruinsma, R. Electrostatics and the assembly of an RNA virus. Phys. Rev. E Stat. Nonlinear Soft Matter Phys. 2005, 71, 061928. [Google Scholar] [CrossRef] [PubMed]
- Li, L.; Wang, L.; Alexov, E. On the energy components governing molecular recognition in the framework of continuum approaches. Front. Mol. Biosci. 2015, 2, 5. [Google Scholar] [CrossRef] [PubMed]
- Li, C.; Li, L.; Zhang, J.; Alexov, E. Highly efficient and exact method for parallelization of grid-based algorithms and its implementation in DelPhi. J. Comput. Chem. 2012, 33, 1960–1966. [Google Scholar] [CrossRef] [Green Version]
- De Castro, C.; Klose, T.; Speciale, I.; Lanzetta, R.; Molinaro, A.; Van Etten, J.L.; Rossmann, M.G. Structure of the chlorovirus PBCV-1 major capsid glycoprotein determined by combining crystallographic and carbohydrate molecular modeling approaches. Proc. Natl. Acad. Sci. USA 2018, 115, E44–E52. [Google Scholar] [CrossRef] [PubMed]
- Caspar, D.L.; Klug, A. Physical principles in the construction of regular viruses. Cold Spring Harb. Symp. Quant. Biol. 1962, 27, 1–24. [Google Scholar] [CrossRef]
- Goddard, T.D.; Huang, C.C.; Ferrin, T.E. Visualizing density maps with UCSF Chimera. J. Struct. Biol. 2007, 157, 281–287. [Google Scholar] [CrossRef] [PubMed]
- Li, L.; Li, C.; Sarkar, S.; Zhang, J.; Witham, S.; Zhang, Z.; Wang, L.; Smith, N.; Petukh, M.; Alexov, E. DelPhi: A comprehensive suite for DelPhi software and associated resources. BMC Biophys. 2012, 5, 9. [Google Scholar] [CrossRef]
- Li, L.; Li, C.; Zhang, Z.; Alexov, E. On the dielectric “constant” of proteins: Smooth dielectric function for macromolecular modeling and its implementation in Delphi. J. Chem. Theory Comput. 2013, 9, 2126–2136. [Google Scholar] [CrossRef] [PubMed]
- Humphrey, W.; Dalke, A.; Schulten, K. VMD: Visual molecular dynamics. J. Mol. Graph. 1996, 14, 33–38. [Google Scholar] [CrossRef]
- Li, L.; Chakravorty, A.; Alexov, E. DelPhiForce, a tool for electrostatic force calculations: Applications to macromolecular binding. J. Comput. Chem. 2017, 38, 584–593. [Google Scholar] [CrossRef] [Green Version]
- Li, L.; Jia, Z.; Peng, Y.; Chakravorty, A.; Sun, L.; Alexov, E. DelPhiForce web server: Electrostatic forces and energy calculations and visualization. Bioinformatics 2017, 33, 3661–3663. [Google Scholar] [CrossRef]
- Vanommeslaeghe, K.; Hatcher, E.; Acharya, C.; Kundu, S.; Zhong, S.; Shim, J.; Darian, E.; Guvench, O.; Lopes, P.; Vorobyov, I. CHARMM general force field: A force field for drug-like molecules compatible with the CHARMM all-atom additive biological force fields. J. Comput. Chem. 2010, 31, 671–690. [Google Scholar] [CrossRef]




| Binding Mode | Polar Solvation Energy (kcal/mol) | Non-Polar Solvation Energy (kcal/mol) | Van der Waals Energy (kcal/mol) | Coulombic Energy (kcal/mol) | Total Binding Energy (kcal/mol) | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| Mean | SD [a] | Mean | SD | Mean | SD | Mean | SD | Mean | SD | |
| 1 | 99.41 | 19.46 | −14.58 | 0.73 | −80.80 | 6.50 | −64.89 | 25.22 | −60.85 | 8.05 |
| 2 | 208.20 | 28.27 | −19.17 | 1.05 | −119.74 | 10.25 | −167.72 | 32.72 | −98.43 | 9.83 |
| 3 | 8.42 | 16.23 | −9.67 | 0.71 | −46.25 | 5.59 | 23.69 | 16.67 | −23.81 | 5.65 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xian, Y.; Karki, C.B.; Silva, S.M.; Li, L.; Xiao, C. The Roles of Electrostatic Interactions in Capsid Assembly Mechanisms of Giant Viruses. Int. J. Mol. Sci. 2019, 20, 1876. https://doi.org/10.3390/ijms20081876
Xian Y, Karki CB, Silva SM, Li L, Xiao C. The Roles of Electrostatic Interactions in Capsid Assembly Mechanisms of Giant Viruses. International Journal of Molecular Sciences. 2019; 20(8):1876. https://doi.org/10.3390/ijms20081876
Chicago/Turabian StyleXian, Yuejiao, Chitra B. Karki, Sebastian Miki Silva, Lin Li, and Chuan Xiao. 2019. "The Roles of Electrostatic Interactions in Capsid Assembly Mechanisms of Giant Viruses" International Journal of Molecular Sciences 20, no. 8: 1876. https://doi.org/10.3390/ijms20081876