The Fuzziness of the Molecular World and Its Perspectives
Abstract
:1. Introduction
2. Some Features of Fuzzy Logic
3. Fuzzy Logic and the Human Nervous System
4. The Methodologies to Implement Fuzzy Sets and Process Fuzzy Logic at the Molecular Level
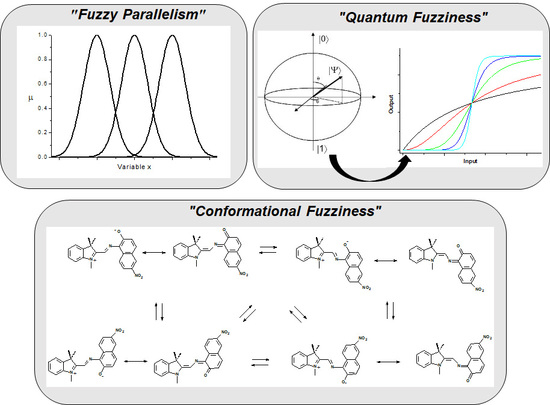
4.1. The “Fuzzy Parallelism” Approach
4.2. “Conformational Fuzziness”
4.3. “Quantum Fuzziness”
5. Perspectives of the Fuzziness of the Molecular World
Funding
Acknowledgments
Conflicts of Interest
References
- Marx, V. The Big Challenges of Big Data. Nature 2013, 498, 255–260. [Google Scholar] [CrossRef] [PubMed]
- Whitfield, J.D.; Love, P.J.; Aspuru-Guzik, A. Computational complexity in electronic structure. Phys. Chem. Chem. Phys. 2013, 15, 397–411. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bishop, C.M. Pattern Recognition and Machine Learning; Springer: New York, NY, USA, 2006. [Google Scholar]
- Gentili, P.L. Untangling Complex Systems: A Grand Challenge for Scienc; CRC Press, Taylor & Francis Group: Boca Raton, FL, USA, 2018. [Google Scholar]
- Gentili, P.L. A strategy to face complexity: The development of chemical artificial intelligence. In Advances in Artificial Life, Evolutionary Computation, and Systems Chemistry; Rossi, F., Piotto, S., Concilio, S., Eds.; Springer: Cham, Switzerland; New York, NY, USA, 2017; Volume 708, pp. 151–160. [Google Scholar]
- Albus, J.S.; Bekey, G.A.; Holland, J.H.; Kanwisher, N.G.; Krichmar, J.L.; Mishkin, M.; Modha, D.S.; Raichle, M.E.; Shepherd, G.M.; Tononi, G. A proposal for a Decade of the Mind initiative. Science 2007, 317, 1321. [Google Scholar] [CrossRef] [PubMed]
- Zadeh, L.A. Outline of a New Approach to the Analysis of Complex Systems and Decision Processes. IEEE Trans. Syst. Man Cyb. 1973, 3, 28–44. [Google Scholar] [CrossRef]
- Zadeh, L.A. A New Direction in AI. Toward a Computational Theory of Perceptions. AI Mag. 2001, 22, 73–84. [Google Scholar]
- Zadeh, L.A. Toward Human Level Machine Intelligence-Is It Achievable? The Need for a Paradigm Shift. IEEE Comput. Intell. Mag. 2008, 3, 11–22. [Google Scholar] [CrossRef]
- Gentili, P.L. Small steps towards the development of chemical artificial intelligent systems. RSC Adv. 2013, 3, 25523–25549. [Google Scholar] [CrossRef]
- Zadeh, L.A. Fuzzy sets. Inform. Control 1965, 8, 338–353. [Google Scholar] [CrossRef] [Green Version]
- Mendel, J.M. Fuzzy logic systems for engineering: A tutorial. Proc. IEEE 1995, 83, 345–377. [Google Scholar] [CrossRef]
- Li, Z.; Chen, G. Integration of Fuzzy Logic and Chaos Theory; Springer Science & Business Media: Dordrecht, The Netherlands, 2006. [Google Scholar]
- Gentili, P.L.; Gotoda, H.; Dolnik, M.; Epstein, I.R. Analysis and prediction of aperiodic hydrodynamic oscillatory time series by feed-forward neural networks, fuzzy logic, and a local nonlinear predictor. Chaos 2015, 25, 013104. [Google Scholar] [CrossRef] [PubMed]
- Kosko, B. Fuzzy cognitive maps. Int. J. Man-Mach. Stud. 1986, 24, 65–75. [Google Scholar] [CrossRef]
- Axelrod, R. Structure of Decision: The Cognitive Maps of Political Elites; Princeton University Press: Princeton, NJ, USA, 1976. [Google Scholar]
- Stach, W.; Kurgan, L.; Pedrycz, W.; Reformat, M. Genetic learning of fuzzy cognitive maps. Fuzzy Sets Syst. 2005, 153, 371–401. [Google Scholar] [CrossRef]
- Zadeh, L.A. The concept of a linguistic variable and its application to approximate reasoning-1. Inf. Sci. 1975, 8, 199–249. [Google Scholar] [CrossRef]
- Mendel, J.M. Type-2 Fuzzy Sets and Systems: An Overview. IEEE Comput. Intell. Mag. 2007, 2, 20–29. [Google Scholar] [CrossRef]
- Castillo, O.; Melin, P. Type-II Fuzzy Logic: Theory and Applications; Springer-Verlag: Heidelberg, Germany, 2008. [Google Scholar]
- Gentili, P.L. The human sensory system as a collection of specialized fuzzifiers: A conceptual framework to inspire new artificial intelligent systems computing with words. J. Intell. Fuzzy Syst. 2014, 27, 2137–2151. [Google Scholar]
- Sandler, U.; Tsitolovsky, L. Neural Cell Behavior and Fuzzy Logic; Springer: New York, NY, USA, 2008. [Google Scholar]
- Paxinos, G.; Mai, J.K. The Human Nervous System, 2nd ed.; Elsevier: San Diego, CA, USA, 2004. [Google Scholar]
- Johnson, E.; Hawken, M.J.; Shapley, R. The spatial transformation of color in the primary visual cortex of the macaque monkey. Nat. Neurosci. 2001, 4, 409–416. [Google Scholar] [CrossRef] [PubMed]
- Friedmann, H.S.; Zhou, H.; von der Heydt, R. The coding of uniform color figures in monkey visual cortex. J. Physiol. (London) 2003, 548, 593–613. [Google Scholar] [CrossRef] [PubMed]
- Gegenfurtner, K.R. Cortical Mechanisms of Colour Vision. Nat. Rev. Neurosci. 2003, 4, 563–572. [Google Scholar] [CrossRef] [PubMed]
- Van Horn, K.S. Constructing a logic of plausible inference: A guide to Cox’s theorem. Int. J. Approx. Reason. 2003, 34, 3–24. [Google Scholar] [CrossRef]
- De Finetti, B.; Machi, A.; Smith, A. Theory of Probability: A Critical Introductory Treatment; John Wiley & Sons: New York, NY, USA, 1992. [Google Scholar]
- Ma, W.J.; Beck, J.M.; Pouget, A. Spiking networks for Bayesian inference and choice. Curr. Opin. Neurobiol. 2008, 18, 217–222. [Google Scholar] [CrossRef] [PubMed]
- Mach, E. Contributions to the Analysis of the Sensations; Open Court Publishing Co.: Chicago, IL, UAS, 1984. [Google Scholar]
- Coletti, G.; Scozzafava, R. Conditional probability, fuzzy sets, and possibility: A unifying view. Fuzzy Sets Syst. 2004, 144, 1–227. [Google Scholar] [CrossRef]
- Kersten, D.; Mamassian, P.; Yuille, A. Object Perception as Bayesian Inference. Annu. Rev. Psychol. 2004, 55, 271–304. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ernst, M.O.; Banks, M.S. Humans integrate visual and haptic information in a statistically optimal fashion. Nature 2002, 415, 429–433. [Google Scholar] [CrossRef] [PubMed]
- Pouget, A.; Deneve, S.; Duhamel, J.-R. A computational perspective on the neural basis of multisensory spatial representations. Nat. Rev. Neurosci. 2002, 3, 741–747. [Google Scholar] [CrossRef] [PubMed]
- Gentili, P.L.; Rightler, A.L.; Heron, B.M.; Gabbutt, C.D. Extending human perception of electromagnetic radiation to the UV region through biologically inspired photochromic fuzzy logic (BIPFUL) systems. Chem. Commun. 2016, 52, 1474–1477. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gentili, P.L.; Rightler, A.L.; Heron, B.M.; Gabbutt, C.D. Discriminating between the UV-A., UV-B and UV-C regions by novel Biologically Inspired Photochromic Fuzzy Logic (BIPFUL) systems: A detailed comparative study. Dyes Pigm. 2016, 135, 169–176. [Google Scholar] [CrossRef]
- Tokuriki, N.; Tawfik, D.S. Protein Dynamism and Evolvability. Science 2009, 324, 203–207. [Google Scholar] [CrossRef] [PubMed]
- Pricer, R.; Gestwicki, J.E.; Mapp, A.K. From Fuzzy to Function: The New Frontier of Protein-Protein Interactions. Acc. Chem. Res. 2017, 50, 584–589. [Google Scholar] [CrossRef] [PubMed]
- Bancaud, A.; Huet, S.; Daigle, N.; Mozziconacci, J.; Beaudouin, J.; Ellenberg, J. Molecular crowding affects diffusion and binding of nuclear proteins in heterochromatin and reveals the fractal organization of chromatin. EMBO J. 2009, 28, 3785–3798. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Dekker, J.; Rippe, K.; Dekker, M.; Kleckner, N. Capturing Chromosome Conformation. Science 2002, 295, 1306–1311. [Google Scholar] [CrossRef] [PubMed]
- Gentili, P.L. The fuzziness of a chromogenic spirooxazine. Dyes Pigm. 2014, 110, 235–248. [Google Scholar] [CrossRef]
- De Luca, A.; Termini, S. A definition of nonprobabilistic entropy in the setting of fuzzy set theory. Inf. Control 1972, 20, 301–312. [Google Scholar] [CrossRef]
- Al-Sharhan, S.; Karray, F.; Gueaieb, W.; Basir, O. Fuzzy entropy: A brief survey. In Proceedings of the IEEE International Fuzzy Systems Conference, Melbourne, Australia, 2–5 December 2001; pp. 1135–1139. [Google Scholar]
- Fuxreiter, M.; Tompa, P. Fuzziness. Structural Disorder in Protein Complexes; Springer: Austin, TX, USA, 2012. [Google Scholar]
- Jeffery, C.J. An introduction to protein moonlighting. Biochem. Soc. Trans. 2014, 42, 1679–1683. [Google Scholar] [CrossRef] [PubMed]
- Zurek, W.H. Decoherence and the Transition from Quantum to Classical. Phys. Today 1991, 44, 36–44. [Google Scholar] [CrossRef]
- Szaciɬowski, K. Digital Information Processing in Molecular Systems. Chem. Rev. 2008, 108, 3481–3548. [Google Scholar] [CrossRef] [PubMed]
- De Silva, A.P. Molecular Logic-based Computation; Royal Society of Chemistry: Cambridge, UK, 2013. [Google Scholar]
- Gentili, P.L. Molecular Processors: From Qubits to Fuzzy Logic. ChemPhysChem. 2011, 12, 739–745. [Google Scholar] [CrossRef] [PubMed]
- Zadegan, R.M.; Jepsen, M.D.E.; Hildebrandt, L.L.; Birkedal, V.; Kjems, J. Construction of a fuzzy and Boolean Logic Gates Based on DNA. Small 2015, 11, 1811–1817. [Google Scholar] [CrossRef] [PubMed]
- George, A.K.; Singh, H. DNA Implementation of Fuzzy Inference Engine: Towards DNA Decision-Making Systems. IEEE Trans. Nanobiosci. 2017, 16, 773–782. [Google Scholar] [CrossRef] [PubMed]
- Bavireddi, H.; Bharate, P.; Kikkeri, R. Use of Boolean and fuzzy logics in lactose glycocluster research. Chem. Commun. 2013, 49, 9185–9187. [Google Scholar] [CrossRef] [PubMed]
- Gentili, P.L. Boolean and fuzzy logic implemented at the molecular level. Chem. Phys. 2007, 336, 64–73. [Google Scholar] [CrossRef]
- Gentili, P.L. Boolean and Fuzzy Logic Gates Based on the Interaction of Flindersine with Bovine Serum Albumin and Tryptophan. J. Phys. Chem. A 2008, 112, 11992–11997. [Google Scholar] [CrossRef] [PubMed]
- Karmakar, S.; Nandi, M.; Mukherjee, S.; Baitalik, S. Polypyridyl-imidazole based smart Ru(II) complex mimicking advanced Boolean and Fuzzy logic functions. Inorg. Chim. Acta 2017, 454, 76–88. [Google Scholar] [CrossRef]
- Xu, X.-Y.; Yan, B. Intelligent Molecular Searcher from Logic Computing Network Based on Eu(III) Functionalized UMOFs for environmental Monitoring. Adv. Funct. Mater. 2017, 27, 1700247. [Google Scholar] [CrossRef]
- Gentili, P.L. The fundamental Fuzzy logic operators and some complex Boolean logic circuits implemented by the chromogenism of a spirooxazine. Phys. Chem. Chem. Phys. 2011, 13, 20335–20344. [Google Scholar] [CrossRef] [PubMed]
- Bhattacharjee, D.; Kim, W.; Chattopadhyay, A.; Waser, R.; Rane, V. Multi-valued and Fuzzy Logic Realization using TaOx Memristive Devices. Sci. Rep. 2018, 8. [Google Scholar] [CrossRef] [PubMed]
- Blachecki, A.; Mech-Piskorz, J.; Gajewska, M.; Mech, K.; Pilaczyk, K.; Szaciɬowski, K. Organotitania-Based Nanostructures as a Suitable Platform for the Implementation of Binary, Ternary, and Fuzzy Logic Systems. ChemPhysChem 2017, 18, 1798–1810. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gentili, P.L.; Horvath, V.; Vanag, V.K.; Epstein, I.R. Belousov-Zhabotinsky “chemical neuron” as a binary and fuzzy logic processor. Int. J. Unconv. Comput. 2012, 8, 177–192. [Google Scholar]
- Gentili, P.L.; Giubila, M.S.; Heron, B.M. Processing Binary and Fuzzy Logic by Chaotic Time Series Generated by a Hydrodynamic Photochemical Oscillator. ChemPhysChem 2017, 18, 1831–1841. [Google Scholar] [CrossRef] [PubMed]
- Gentili, P.L.; Giubila, M.S.; Germani, R.; Romani, A.; Nicoziani, A.; Spalletti, A.; Heron, B.M. Optical Communication among Oscillatory Reactions and Photo-Excitable Systems: UV and Visible Radiation Can Synchronize Artificial Neuron Models. Angew. Chem. Int. Ed. 2017, 56, 7535–7540. [Google Scholar] [CrossRef] [PubMed]
- Gentili, P.L.; Giubila, M.S.; Germani, R.; Heron, B.M. Photochromic and luminescent compounds as artificial neuron models. Dyes Pigm. 2018, 156, 149–159. [Google Scholar] [CrossRef]
- Zlotnik, A.; Nagao, R.; Kis, I.Z.; Li, S., Jr. Phase-selective entrainment of nonlinear oscillator ensembles. Nat. Commun. 2016, 7, 10788. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Horvath, V.; Gentili, P.L.; Vanag, V.K.; Epstein, I.R. Pulsed-Coupled Chemical Oscillators with Time Delay. Angew. Chem. Int. Ed. 2012, 51, 6878–6881. [Google Scholar] [CrossRef] [PubMed]
- Hagiya, M.; Konagaya, A.; Kobayashi, S.; Saito, H.; Murata, S. Molecular robots with sensors and intelligence. Acc. Chem. Res. 2014, 47, 1681–1690. [Google Scholar] [CrossRef] [PubMed]
- Adamatzky, A.; de Lacy Costello, B.; Melhuish, C.; Ratcliffe, N. Experimental implementation of mobile robot taxis with onboard Belousov-Zhabotinsky chemical medium. Mater. Sci. Eng. 2004, 24, 541–548. [Google Scholar] [CrossRef]
- Hess, H.; Ross, J.L. Non-equilibrium assembly of microtubules: From molecules to autonomous chemical robots. Chem. Soc. Rev. 2017, 46, 5570–5587. [Google Scholar] [CrossRef] [PubMed]
- Grančič, P.; Štěpánek, F. Chemical swarm robots in Handbook of Collective Robotics–Fundamentals and Challenges; Kernbach, S., Ed.; Pan Stanford Publishing: Singapore, 2011. [Google Scholar]
- Lund, K.; Manzo, A.J.; Dabby, N.; Michelotti, N.; Johnson-Buck, A.; Nangreave, J.; Taylor, S.; Pei, R.; Stojanovic, M.N.; Walter, N.G.; et al. Molecular robots guided by prescriptive landscapes. Nature 2010, 465, 206–210. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kassem, S.; Lee, A.T.L.; Leigh, D.A.; Markevicius, A.; Solà, J. Pick-up, transport and release of a molecular cargo using a small-molecule robotic arm. Nat. Chem. 2016, 8, 138–143. [Google Scholar] [CrossRef] [PubMed]










© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gentili, P.L. The Fuzziness of the Molecular World and Its Perspectives. Molecules 2018, 23, 2074. https://doi.org/10.3390/molecules23082074
Gentili PL. The Fuzziness of the Molecular World and Its Perspectives. Molecules. 2018; 23(8):2074. https://doi.org/10.3390/molecules23082074
Chicago/Turabian StyleGentili, Pier Luigi. 2018. "The Fuzziness of the Molecular World and Its Perspectives" Molecules 23, no. 8: 2074. https://doi.org/10.3390/molecules23082074