Multiscale Computation and Machine Learning
Share This Topical Collection
Editors
 Prof. Dr. Yalchin Efendiev
Prof. Dr. Yalchin Efendiev
 Prof. Dr. Yalchin Efendiev
Prof. Dr. Yalchin Efendiev
E-Mail
Website
Collection Editor
Institute for Scientific Computation (ISC), Department of Mathematics, ISC, Texas University, College Station, TX 77843, USA
Interests: multiscale; porous media; upscaling; flow; transport; multiscale finite element
Special Issues, Collections and Topics in MDPI journals
 Prof. Dr. Eric T. Chung
Prof. Dr. Eric T. Chung
 Prof. Dr. Eric T. Chung
Prof. Dr. Eric T. Chung
E-Mail
Website
Collection Editor
Department of Mathematics, Chinese University of Hong Kong, Hong Kong, China
Interests: discontinuous Galerkin methods; computational wave propagation; fluid flow in heterogeneous media; multiscale model reduction techniques; adaptivity for multiscale problems; domain decomposition methods; data-driven computational methods; numerical upscaling
Special Issues, Collections and Topics in MDPI journals
Topical Collection Information
Dear Colleagues,
Multiscale Computation and Machine Learning play an increasingly important role in many applications. Many real-world applications rely on multiscale simulations.These simulations often use pre-computations to train macroscale quantities. In this regard, machine learning approaches can be used to accelerate and enhance multiscale simulations. On the other hand, multiscale models and simulations can be used in designing machine learning algorithms that are suitable for solving challenging applications. This collection aims at creating a common platform for publishing papers on multiscale computation, machine learning, and their combination.
The aim of this Topical Collection is to bring together recent scientific advances, reviews, communications, and short notes dealing with multiscale simulations and machine learning.
Prof. Dr. Yalchin Efendiev
Prof. Dr. Eric T. Chung
Collection Editors
Manuscript Submission Information
Manuscripts should be submitted online at www.mdpi.com by registering and logging in to this website. Once you are registered, click here to go to the submission form. Manuscripts can be submitted until the deadline. All submissions that pass pre-check are peer-reviewed. Accepted papers will be published continuously in the journal (as soon as accepted) and will be listed together on the collection website. Research articles, review articles as well as short communications are invited. For planned papers, a title and short abstract (about 100 words) can be sent to the Editorial Office for announcement on this website.
Submitted manuscripts should not have been published previously, nor be under consideration for publication elsewhere (except conference proceedings papers). All manuscripts are thoroughly refereed through a single-blind peer-review process. A guide for authors and other relevant information for submission of manuscripts is available on the Instructions for Authors page. Mathematics is an international peer-reviewed open access semimonthly journal published by MDPI.
Please visit the Instructions for Authors page before submitting a manuscript.
The Article Processing Charge (APC) for publication in this open access journal is 2600 CHF (Swiss Francs).
Submitted papers should be well formatted and use good English. Authors may use MDPI's
English editing service prior to publication or during author revisions.
Keywords
- multiscale
- machine learning
- simulations
- porous media
- finite element
- finite volume
Published Papers (4 papers)
Open AccessFeature PaperArticle
Partial Learning Using Partially Explicit Discretization for Multicontinuum/Multiscale Problems with Limited Observation: Dual Continuum Heterogeneous Poroelastic Media Simulation
by
Aleksei Tyrylgin, Sergei Stepanov, Dmitry Ammosov, Aleksandr Grigorev and Maria Vasilyeva
Cited by 5 | Viewed by 1324
Abstract
In this paper, we consider the poroelasticity problem in heterogeneous media. The mathematical model is described by a coupled system of equations for displacement and pressure in the coupled dual continuum porous media. We propose a new method based on hybrid explicit–implicit (HEI)
[...] Read more.
In this paper, we consider the poroelasticity problem in heterogeneous media. The mathematical model is described by a coupled system of equations for displacement and pressure in the coupled dual continuum porous media. We propose a new method based on hybrid explicit–implicit (HEI) learning to solve the poroelasticity problem in dual continuum heterogeneous media. We use a finite element method with standard linear basis functions for spatial approximation. We apply the explicit–implicit time scheme, where the explicit scheme is used for the low-conductive continuum and the implicit scheme for the high-conductive. The fixed-strain splitting scheme is used to accelerate the computation and decouple the flow and mechanics problems. The main idea of the proposed method is partial learning of particular degrees of freedom of the high-conductive continuum’s pressure (implicit part of the flow). First, we train a deep neural network (DNN) to obtain values of the implicit part of the flow at some spatial points at some time moments. Then, we apply the Discrete Empirical Interpolation Method (DEIM) combined with Proper Orthogonal Decomposition (POD) to restore the complete implicit parts and perform linear interpolation over time. Consequently, we treat the high-conductive continuum’s pressure as a known function and use it to find the other continuum’s pressure and displacements. Numerical results for the two-dimensional model problem are presented. The results demonstrate that the proposed method provides fast and accurate predictions.
Full article
►▼
Show Figures
Open AccessArticle
Contrast-Independent Partially Explicit Time Discretizations for Quasi Gas Dynamics
by
Boris Chetverushkin, Yalchin Efendiev and Wing Tat Leung
Cited by 3 | Viewed by 1318
Abstract
In the paper, we study a design and stability of contrast-independent partially explicit time discretizations for Quasi-Gas-Dynamics (QGD) Equations in multiscale high-contrast media. In our previous works, we have introduced contrast-independent partially explicit time discretizations. In this paper, we extend these ideas to
[...] Read more.
In the paper, we study a design and stability of contrast-independent partially explicit time discretizations for Quasi-Gas-Dynamics (QGD) Equations in multiscale high-contrast media. In our previous works, we have introduced contrast-independent partially explicit time discretizations. In this paper, we extend these ideas to multiscale QGD problems. Because of high contrast, explicit methods require a very small time stepping. By designing appropriate spatial splitting and temporal splitting, partially explicit methods remove this constraint. The proposed partially explicit time discretization consists of two steps. First, we split the space into contrast dependent (fast) and contrast independent (slow) components on a coarse grid that is much larger compared to spatial heterogeneities. Secondly, we design a temporal splitting algorithm in a such way that it is stable and the time step is independent of the contrast and only depends on the coarse mesh size. Using proposed method, a few degrees of freedom are treated implicitly and the approach is mostly explicit. We prove that the proposed splitting is unconditionally stable under some suitable conditions formulated for the second space (slow). We present numerical results and show that the proposed methods provide results similar to implicit methods with the time step that is independent of the contrast.
Full article
►▼
Show Figures
Open AccessArticle
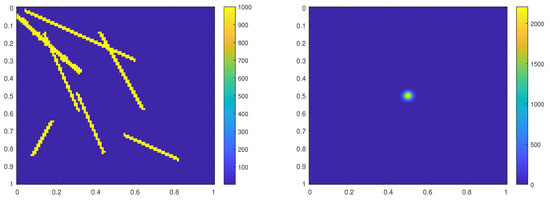
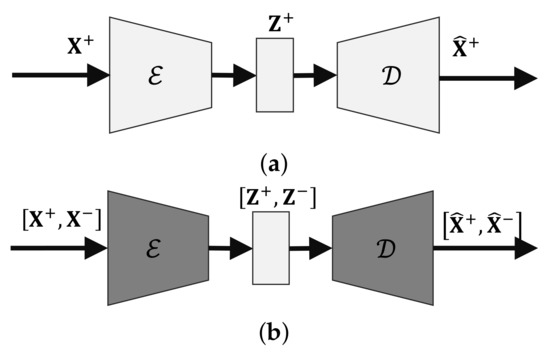
Latent-Insensitive Autoencoders for Anomaly Detection
by
Muhammad S. Battikh and Artem A. Lenskiy
Cited by 2 | Viewed by 1834
Abstract
Reconstruction-based approaches to anomaly detection tend to fall short when applied to complex datasets with target classes that possess high inter-class variance. Similar to the idea of self-taught learning used in transfer learning, many domains are rich with similar unlabeled datasets that could
[...] Read more.
Reconstruction-based approaches to anomaly detection tend to fall short when applied to complex datasets with target classes that possess high inter-class variance. Similar to the idea of self-taught learning used in transfer learning, many domains are rich with similar unlabeled datasets that could be leveraged as a proxy for out-of-distribution samples. In this paper we introduce the latent-insensitive autoencoder (LIS-AE) where unlabeled data from a similar domain are utilized as negative examples to shape the latent layer (bottleneck) of a regular autoencoder such that it is only capable of reconstructing one task. We provide theoretical justification for the proposed training process and loss functions along with an extensive ablation study highlighting important aspects of our model. We test our model in multiple anomaly detection settings presenting quantitative and qualitative analysis showcasing the significant performance improvement of our model for anomaly detection tasks.
Full article
►▼
Show Figures
Open AccessArticle
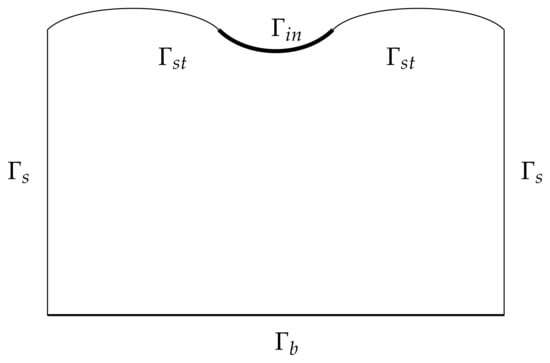
Multiscale Multiphysics Modeling of the Infiltration Process in the Permafrost
by
Sergei Stepanov, Djulustan Nikiforov and Aleksandr Grigorev
Cited by 7 | Viewed by 1614
Abstract
In this work, we design a multiscale simulation method based on the Generalized Multiscale Finite Element Method (GMsFEM) for numerical modeling of fluid seepage under permafrost condition in heterogeneous soils. The complex multiphysical model consists of the coupled Richards equation and the Stefan
[...] Read more.
In this work, we design a multiscale simulation method based on the Generalized Multiscale Finite Element Method (GMsFEM) for numerical modeling of fluid seepage under permafrost condition in heterogeneous soils. The complex multiphysical model consists of the coupled Richards equation and the Stefan problem. These problems often contain heterogeneities due to variations of soil properties. For this reason, we design coarse-grid spaces for the multiphysical problem and design special algorithms for solving the overall problem. A numerical method has been tested on two- and three-dimensional model problems. A a quasi-real geometry with a complex surface is considered for the three-dimensional case. We demonstrate the efficiency and accuracy of the proposed method using several representative numerical results.
Full article
►▼
Show Figures