Journal Description
AppliedMath
AppliedMath
is an international, peer-reviewed, open access journal on applied mathematics published quarterly online by MDPI.
- Open Access— free for readers, with article processing charges (APC) paid by authors or their institutions.
- Rapid Publication: manuscripts are peer-reviewed and a first decision is provided to authors approximately 30.7 days after submission; acceptance to publication is undertaken in 6.6 days (median values for papers published in this journal in the second half of 2023).
- Recognition of Reviewers: APC discount vouchers, optional signed peer review, and reviewer names published annually in the journal.
- AppliedMath is a companion journal of Mathematics.
Latest Articles
Minimal Terracini Loci in a Plane and Their Generalizations
AppliedMath 2024, 4(2), 529-543; https://doi.org/10.3390/appliedmath4020028 - 17 Apr 2024
Abstract
We study properties of the minimal Terracini loci, i.e., families of certain zero-dimensional schemes, in a projective plane. Among the new results here are: a maximality theorem and the existence of arbitrarily large gaps or non-gaps for the integers x for which the
[...] Read more.
We study properties of the minimal Terracini loci, i.e., families of certain zero-dimensional schemes, in a projective plane. Among the new results here are: a maximality theorem and the existence of arbitrarily large gaps or non-gaps for the integers x for which the minimal Terracini locus in degree d is non-empty. We study similar theorems for the critical schemes of the minimal Terracini sets. This part is framed in a more general framework.
Full article
Open AccessArticle
Spontaneous Imbibition and an Interface-Electrostatics-Based Model of the Transition Zone Thickness of Hydrocarbon Reservoirs and Their Theoretical Interpretations
by
Mumuni Amadu and Adango Miadonye
AppliedMath 2024, 4(2), 517-528; https://doi.org/10.3390/appliedmath4020027 - 16 Apr 2024
Abstract
►▼
Show Figures
The transition zone (TZ) of hydrocarbon reservoirs is an integral part of the hydrocarbon pool which contains a substantial fraction of the deposit, particularly in carbonate petroleum systems. Consequently, knowledge of its thickness and petrophysical properties, viz. its pore size distribution and wettability
[...] Read more.
The transition zone (TZ) of hydrocarbon reservoirs is an integral part of the hydrocarbon pool which contains a substantial fraction of the deposit, particularly in carbonate petroleum systems. Consequently, knowledge of its thickness and petrophysical properties, viz. its pore size distribution and wettability characteristic, is critical to optimizing hydrocarbon production in this zone. Using classical formation evaluation techniques, the thickness of the transition zone has been estimated, using well logging methods including resistivity and Nuclear Magnetic Resonance, among others. While hydrocarbon fluids’ accumulation in petroleum reservoirs occurs due to the migration and displacement of originally water-filled potential structural and stratigraphic traps, the development of their TZ integrates petrophysical processes that combine spontaneous capillary imbibition and wettability phenomena. In the literature, wettability phenomena have been shown to also be governed by electrostatic phenomena. Therefore, given that reservoir rocks are aggregates of minerals with ionizable surface groups that facilitate the development of an electric double layer, a definite theoretical relationship between the TZ and electrostatic theory must be feasible. Accordingly, a theoretical approach to estimating the TZ thickness, using the electrostatic theory and based on the electric double layer theory, is attractive, but this is lacking in the literature. Herein, we fill the knowledge gap by using the interfacial electrostatic theory based on the fundamental tenets of the solution to the Poisson–Boltzmann mean field theory. Accordingly, we have used an existing model of capillary rise based on free energy concepts to derive a capillary rise equation that can be used to theoretically predict observations based on the TZ thickness of different reservoir rocks, using well-established formation evaluation methods. The novelty of our work stems from the ability of the model to theoretically and accurately predict the TZ thickness of the different lithostratigraphic units of hydrocarbon reservoirs, because of the experimental accessibility of its model parameters.
Full article
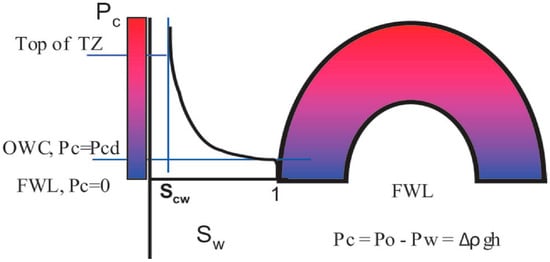
Figure 1
Open AccessArticle
Sums of Independent Circular Random Variables and Maximum Likelihood Circular Uniformity Tests Based on Nonnegative Trigonometric Sums Distributions
by
Juan José Fernández-Durán and María Mercedes Gregorio-Domínguez
AppliedMath 2024, 4(2), 495-516; https://doi.org/10.3390/appliedmath4020026 - 09 Apr 2024
Abstract
►▼
Show Figures
The sum of independent circular uniformly distributed random variables is also circular uniformly distributed. In this study, it is shown that a family of circular distributions based on nonnegative trigonometric sums (NNTS) is also closed under summation. Given the flexibility of NNTS circular
[...] Read more.
The sum of independent circular uniformly distributed random variables is also circular uniformly distributed. In this study, it is shown that a family of circular distributions based on nonnegative trigonometric sums (NNTS) is also closed under summation. Given the flexibility of NNTS circular distributions to model multimodality and skewness, these are good candidates for use as alternative models to test for circular uniformity to detect different deviations from the null hypothesis of circular uniformity. The circular uniform distribution is a member of the NNTS family, but in the NNTS parameter space, it corresponds to a point on the boundary of the parameter space, implying that the regularity conditions are not satisfied when the parameters are estimated by using the maximum likelihood method. Two NNTS tests for circular uniformity were developed by considering the standardised maximum likelihood estimator and the generalised likelihood ratio. Given the nonregularity condition, the critical values of the proposed NNTS circular uniformity tests were obtained via simulation and interpolated for any sample size by the fitting of regression models. The validity of the proposed NNTS circular uniformity tests was evaluated by generating NNTS models close to the circular uniformity null hypothesis.
Full article
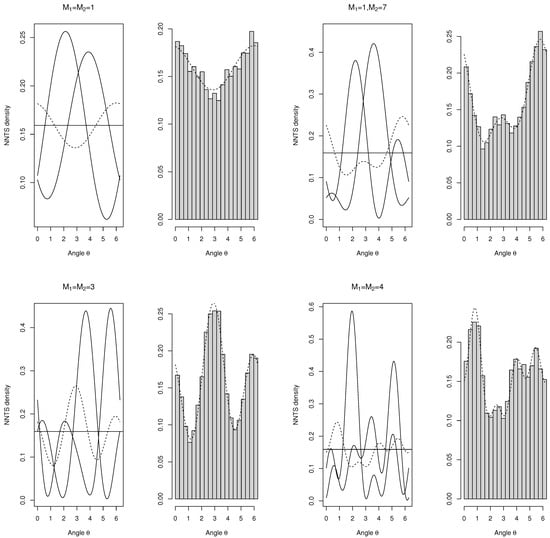
Figure 1
Open AccessArticle
A New Approach to Understanding Quantum Mechanics: Illustrated Using a Pedagogical Model over ℤ2
by
David Ellerman
AppliedMath 2024, 4(2), 468-494; https://doi.org/10.3390/appliedmath4020025 - 09 Apr 2024
Abstract
►▼
Show Figures
The new approach to quantum mechanics (QM) is that the mathematics of QM is the linearization of the mathematics of partitions (or equivalence relations) on a set. This paper develops those ideas using vector spaces over the field
[...] Read more.
The new approach to quantum mechanics (QM) is that the mathematics of QM is the linearization of the mathematics of partitions (or equivalence relations) on a set. This paper develops those ideas using vector spaces over the field
Figure 1
Open AccessArticle
Analyzing Small-Signal Stability in a Multi-Source Single-Area Power System with a Load-Frequency Controller Coordinated with a Photovoltaic System
by
Ghazanfar Shahgholian and Arman Fathollahi
AppliedMath 2024, 4(2), 452-467; https://doi.org/10.3390/appliedmath4020024 - 03 Apr 2024
Abstract
►▼
Show Figures
The frequency deviation from the nominal working frequency in power systems is a consequence of the imbalance between total electrical loads and the aggregate power supplied by production units. The sensitivity of energy system frequency to both minor and major load variations underscore
[...] Read more.
The frequency deviation from the nominal working frequency in power systems is a consequence of the imbalance between total electrical loads and the aggregate power supplied by production units. The sensitivity of energy system frequency to both minor and major load variations underscore the need for effective frequency load control mechanisms. In this paper, frequency load control in single-area power system with multi-source energy is analysed and simulated. Also, the effect of the photovoltaic system on the frequency deviation changes in the energy system is shown. In the single area energy system, the dynamics of thermal turbine with reheat, thermal turbine without reheat and hydro turbine are considered. The simulation results using Simulink/Matlab and model analysis using eigenvalue analysis show the dynamic behaviour of the power system in response to changes in the load.
Full article

Figure 1
Open AccessArticle
An Explicit Form of Ramp Function
by
John Constantine Venetis
AppliedMath 2024, 4(2), 442-451; https://doi.org/10.3390/appliedmath4020023 - 02 Apr 2024
Abstract
In this paper, an analytical exact form of the ramp function is presented. This seminal function constitutes a fundamental concept of the digital signal processing theory and is also involved in many other areas of applied sciences and engineering. In particular, the ramp
[...] Read more.
In this paper, an analytical exact form of the ramp function is presented. This seminal function constitutes a fundamental concept of the digital signal processing theory and is also involved in many other areas of applied sciences and engineering. In particular, the ramp function is performed in a simple manner as the pointwise limit of a sequence of real and continuous functions with pointwise convergence. This limit is zero for strictly negative values of the real variable
Open AccessArticle
Enhancing COVID-19 Prevalence Forecasting: A Hybrid Approach Integrating Epidemic Differential Equations and Recurrent Neural Networks
by
Liang Kong, Yanhui Guo and Chung-wei Lee
AppliedMath 2024, 4(2), 427-441; https://doi.org/10.3390/appliedmath4020022 - 01 Apr 2024
Abstract
►▼
Show Figures
Accurate forecasting of the coronavirus disease 2019 (COVID-19) spread is indispensable for effective public health planning and the allocation of healthcare resources at all levels of governance, both nationally and globally. Conventional prediction models for the COVID-19 pandemic often fall short in precision,
[...] Read more.
Accurate forecasting of the coronavirus disease 2019 (COVID-19) spread is indispensable for effective public health planning and the allocation of healthcare resources at all levels of governance, both nationally and globally. Conventional prediction models for the COVID-19 pandemic often fall short in precision, due to their reliance on homogeneous time-dependent transmission rates and the oversight of geographical features when isolating study regions. To address these limitations and advance the predictive capabilities of COVID-19 spread models, it is imperative to refine model parameters in accordance with evolving insights into the disease trajectory, transmission rates, and the myriad economic and social factors influencing infection. This research introduces a novel hybrid model that combines classic epidemic equations with a recurrent neural network (RNN) to predict the spread of the COVID-19 pandemic. The proposed model integrates time-dependent features, namely the numbers of individuals classified as susceptible, infectious, recovered, and deceased (SIRD), and incorporates human mobility from neighboring regions as a crucial spatial feature. The study formulates a discrete-time function within the infection component of the SIRD model, ensuring real-time applicability while mitigating overfitting and enhancing overall efficiency compared to various existing models. Validation of the proposed model was conducted using a publicly available COVID-19 dataset sourced from Italy. Experimental results demonstrate the model’s exceptional performance, surpassing existing spatiotemporal models in three-day ahead forecasting. This research not only contributes to the field of epidemic modeling but also provides a robust tool for policymakers and healthcare professionals to make informed decisions in managing and mitigating the impact of the COVID-19 pandemic.
Full article
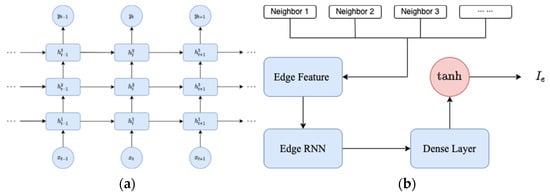
Figure 1
Open AccessArticle
The Reliability Inference for Multicomponent Stress–Strength Model under the Burr X Distribution
by
Yuhlong Lio, Ding-Geng Chen, Tzong-Ru Tsai and Liang Wang
AppliedMath 2024, 4(1), 394-426; https://doi.org/10.3390/appliedmath4010021 - 17 Mar 2024
Abstract
►▼
Show Figures
The reliability of the multicomponent stress–strength system was investigated under the two-parameter Burr X distribution model. Based on the structure of the system, the type II censored sample of strength and random sample of stress were obtained for the study. The maximum likelihood
[...] Read more.
The reliability of the multicomponent stress–strength system was investigated under the two-parameter Burr X distribution model. Based on the structure of the system, the type II censored sample of strength and random sample of stress were obtained for the study. The maximum likelihood estimators were established by utilizing the type II censored Burr X distributed strength and complete random stress data sets collected from the multicomponent system. Two related approximate confidence intervals were achieved by utilizing the delta method under the asymptotic normal distribution theory and parametric bootstrap procedure. Meanwhile, point and confidence interval estimators based on alternative generalized pivotal quantities were derived. Furthermore, a likelihood ratio test to infer the equality of both scalar parameters is provided. Finally, a practical example is provided for illustration.
Full article
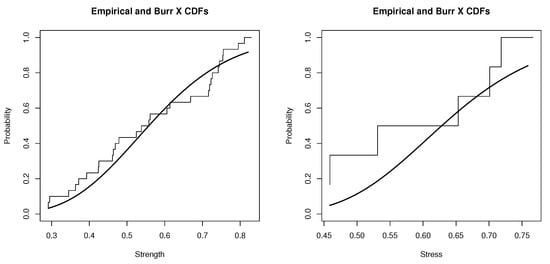
Figure 1
Open AccessArticle
Inverses for Fourth-Degree Permutation Polynomials Modulo 32Ψ or 96Ψ, with Ψ as a Product of Different Prime Numbers Greater than Three
by
Lucian Trifina, Daniela Tărniceriu and Ana-Mirela Rotopănescu
AppliedMath 2024, 4(1), 383-393; https://doi.org/10.3390/appliedmath4010020 - 16 Mar 2024
Abstract
In this paper, we address the inverse of a true fourth-degree permutation polynomial (4-PP), modulo a positive integer of the form
In this paper, we address the inverse of a true fourth-degree permutation polynomial (4-PP), modulo a positive integer of the form
Open AccessReview
Four Measures of Association and Their Representations in Terms of Copulas
by
Michel Adès, Serge B. Provost and Yishan Zang
AppliedMath 2024, 4(1), 363-382; https://doi.org/10.3390/appliedmath4010019 - 02 Mar 2024
Abstract
►▼
Show Figures
Four measures of association, namely, Spearman’s
Four measures of association, namely, Spearman’s
Figure 1
Open AccessArticle
Pricing Contingent Claims in a Two-Interest-Rate Multi-Dimensional Jump-Diffusion Model via Market Completion
by
Alexander Melnikov and Pouneh Mohammadi Nejad
AppliedMath 2024, 4(1), 348-362; https://doi.org/10.3390/appliedmath4010018 - 02 Mar 2024
Abstract
This paper investigates a financial market where asset prices follow a multi-dimensional Brownian motion process and a multi-dimensional Poisson process characterized by diverse credit and deposit rates where the credit rate is higher than the deposit rate. The focus extends to evaluating European
[...] Read more.
This paper investigates a financial market where asset prices follow a multi-dimensional Brownian motion process and a multi-dimensional Poisson process characterized by diverse credit and deposit rates where the credit rate is higher than the deposit rate. The focus extends to evaluating European options by establishing upper and lower hedging prices through a transition to a suitable auxiliary market. Introducing a lemma elucidates the same solution to the pricing problem in both markets under specific conditions. Additionally, we address the minimization of shortfall risk and determine no-arbitrage price bounds within the framework of incomplete markets. This study provides a comprehensive understanding of the challenges posed by the multi-dimensional jump-diffusion model and varying interest rates in financial markets.
Full article
Open AccessArticle
A Block Hybrid Method with Equally Spaced Grid Points for Third-Order Initial Value Problems
by
Salma A. A. Ahmedai Abd Allah, Precious Sibanda, Sicelo P. Goqo, Uthman O. Rufai, Hloniphile Sithole Mthethwa and Osman A. I. Noreldin
AppliedMath 2024, 4(1), 320-347; https://doi.org/10.3390/appliedmath4010017 - 01 Mar 2024
Abstract
In this paper, we extend the block hybrid method with equally spaced intra-step points to solve linear and nonlinear third-order initial value problems. The proposed block hybrid method uses a simple iteration scheme to linearize the equations. Numerical experimentation demonstrates that equally spaced
[...] Read more.
In this paper, we extend the block hybrid method with equally spaced intra-step points to solve linear and nonlinear third-order initial value problems. The proposed block hybrid method uses a simple iteration scheme to linearize the equations. Numerical experimentation demonstrates that equally spaced grid points for the block hybrid method enhance its speed of convergence and accuracy compared to other conventional block hybrid methods in the literature. This improvement is attributed to the linearization process, which avoids the use of derivatives. Further, the block hybrid method is consistent, stable, and gives rapid convergence to the solutions. We show that the simple iteration method, when combined with the block hybrid method, exhibits impressive convergence characteristics while preserving computational efficiency. In this study, we also implement the proposed method to solve the nonlinear Jerk equation, producing comparable results with other methods used in the literature.
Full article
(This article belongs to the Special Issue Contemporary Iterative Methods with Applications in Applied Sciences)
►▼
Show Figures
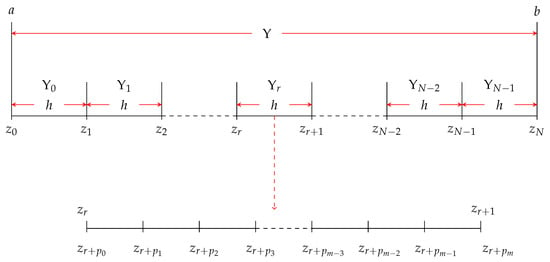
Figure 1
Open AccessArticle
Comparative Study of Monte Carlo Simulation and the Deterministic Model to Analyze Thermal Insulation Costs
by
Marco Antonio Montufar Benítez, Jaime Mora Vargas, José Raúl Castro Esparza, Héctor Rivera Gómez and Oscar Montaño Arango
AppliedMath 2024, 4(1), 305-319; https://doi.org/10.3390/appliedmath4010016 - 01 Mar 2024
Abstract
►▼
Show Figures
The main purpose of this paper is to implement a simulation model in @RISKTM and study the impact of incorporating random variables, such as the degree days in a traditional deterministic model, for calculating the optimum thickness of thermal insulation in walls.
[...] Read more.
The main purpose of this paper is to implement a simulation model in @RISKTM and study the impact of incorporating random variables, such as the degree days in a traditional deterministic model, for calculating the optimum thickness of thermal insulation in walls. Currently, green buildings have become important because of the increasing worldwide interest in the reduction of environmental pollution. One method of saving energy is to use thermal insulation. The optimum thickness of these insulators has traditionally been calculated using deterministic models. With the information generated from real data using the degree days required in a certain zone in Palestine during winter, random samples of the degree days required annually in this town were generated for periods of 10, 20, 50, and 70 years. The results showed that the probability of exceeding the net present value of the cost calculated using deterministic analysis ranges from 0% to 100%, without regard to the inflation rate. The results also show that, for design lifetimes greater than 40 years, the risk of overspending is lower if the building lasts longer than the period for which it was designed. Moreover, this risk is transferred to whomever will pay the operating costs of heating the building. The contribution of this research is twofold: (a) a stochastic approach is incorporated into the traditional models that determine the optimum thickness of thermal insulation used in buildings, by introducing the variability of the degree days required in a given region; (b) a measure of the economic risk incurred by building heating is established as a function of the years of use for which the building is designed and the number of years it is actually used.
Full article
Figure 1
Open AccessArticle
A Strange Result Regarding Some MHD Motions of Generalized Burgers’ Fluids with a Differential Expression of Shear Stress on the Boundary
by
Constantin Fetecau, Costică Moroşanu and Shehraz Akhtar
AppliedMath 2024, 4(1), 289-304; https://doi.org/10.3390/appliedmath4010015 - 01 Mar 2024
Abstract
►▼
Show Figures
In this work, we investigate isothermal MHD motions of a large class of rate type fluids through a porous medium between two infinite horizontal parallel plates when a differential expression of the non-trivial shear stress is prescribed on the boundary. Exact expressions are
[...] Read more.
In this work, we investigate isothermal MHD motions of a large class of rate type fluids through a porous medium between two infinite horizontal parallel plates when a differential expression of the non-trivial shear stress is prescribed on the boundary. Exact expressions are provided for the dimensionless steady state velocities, shear stresses and Darcy’s resistances. Obtained solutions can be used to find the necessary time to touch the steady state or to bring to light certain characteristics of the fluid motion. Graphical representations showed the fluid moves slower in presence of a magnetic field or porous medium. In addition, contrary to our expectations, the volume flux across a plane orthogonal to the velocity vector per unit width of this plane is zero. Finally, based on a simple remark regarding the governing equations of velocity and shear stress for MHD motions of incompressible generalized Burgers’ fluids between infinite parallel plates, provided were the first exact solutions for MHD motions of these fluids when the two plates apply oscillatory or constant shear stresses to the fluid. This important remark offers the possibility to solve any isothermal MHD motion of these fluids between infinite parallel plates or over an infinite plate when the non-trivial shear stress is prescribed on the boundary. As an application, steady state solutions for MHD motions of same fluids have been developed when a differential expression of the fluid velocity is prescribed on the boundary.
Full article
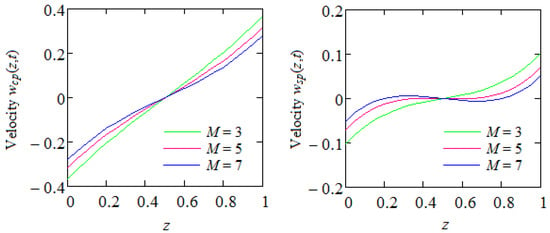
Figure 1
Open AccessArticle
Exploratory Analysis of Distributional Data Using the Quantile Method
by
Manabu Ichino
AppliedMath 2024, 4(1), 261-288; https://doi.org/10.3390/appliedmath4010014 - 17 Feb 2024
Abstract
►▼
Show Figures
The quantile method transforms each complex object described by different histogram values to a common number of quantile vectors. This paper retraces the authors’ research, including a principal component analysis, unsupervised feature selection using hierarchical conceptual clustering, and lookup table regression model. The
[...] Read more.
The quantile method transforms each complex object described by different histogram values to a common number of quantile vectors. This paper retraces the authors’ research, including a principal component analysis, unsupervised feature selection using hierarchical conceptual clustering, and lookup table regression model. The purpose is to show that this research is essentially based on the monotone property of quantile vectors and works cooperatively in the exploratory analysis of the given distributional data.
Full article
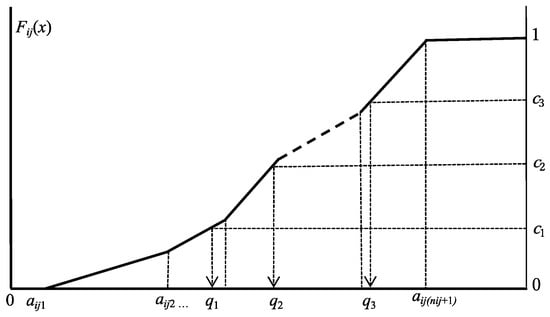
Figure 1
Open AccessArticle
On Some Properties of a Complete Quadrangle
by
Vladimir Volenec, Marija Šimić Horvath and Ema Jurkin
AppliedMath 2024, 4(1), 250-260; https://doi.org/10.3390/appliedmath4010013 - 05 Feb 2024
Abstract
►▼
Show Figures
In this paper, we study the properties of a complete quadrangle in the Euclidean plane. The proofs are based on using rectangular coordinates symmetrically on four vertices and four parameters
In this paper, we study the properties of a complete quadrangle in the Euclidean plane. The proofs are based on using rectangular coordinates symmetrically on four vertices and four parameters
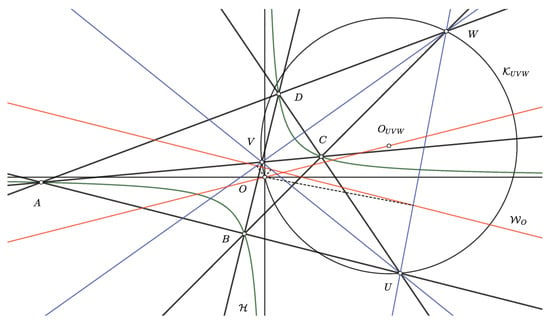
Figure 1
Open AccessFeature PaperArticle
Convection of Physical Quantities of Random Density
by
Elisabetta Barletta, Sorin Dragomir and Francesco Esposito
AppliedMath 2024, 4(1), 225-249; https://doi.org/10.3390/appliedmath4010012 - 05 Feb 2024
Abstract
We study the random flow, through a thin cylindrical tube, of a physical quantity of random density, in the presence of random sinks and sources. We model convection in terms of the expectations of the flux and density and solve the initial value
[...] Read more.
We study the random flow, through a thin cylindrical tube, of a physical quantity of random density, in the presence of random sinks and sources. We model convection in terms of the expectations of the flux and density and solve the initial value problem for the resulting convection equation. We propose a difference scheme for the convection equation, that is both stable and satisfies the Courant–Friedrichs–Lewy test, and estimate the difference between the exact and approximate solutions.
Full article
Open AccessArticle
Decompositions of the λ-Fold Complete Mixed Graph into Mixed 6-Stars
by
Robert Gardner and Kazeem Kosebinu
AppliedMath 2024, 4(1), 211-224; https://doi.org/10.3390/appliedmath4010011 - 05 Feb 2024
Abstract
►▼
Show Figures
Graph and digraph decompositions are a fundamental part of design theory. Probably the best known decompositions are related to decomposing the complete graph into 3-cycles (which correspond to Steiner triple systems), and decomposing the complete digraph into orientations of a 3-cycle (the two
[...] Read more.
Graph and digraph decompositions are a fundamental part of design theory. Probably the best known decompositions are related to decomposing the complete graph into 3-cycles (which correspond to Steiner triple systems), and decomposing the complete digraph into orientations of a 3-cycle (the two possible orientations of a 3-cycle correspond to directed triple systems and Mendelsohn triple systems). Decompositions of the
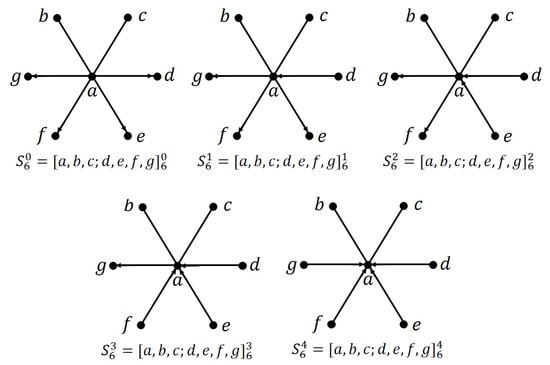
Figure 1
Open AccessArticle
Cell-Cycle Synchronization Prior to Radiotherapy: A Mathematical Model of the Use of Gemcitabine on Melanoma Xenografts
by
Frederika Rentzeperis, Benjamin Coleman and Dorothy Wallace
AppliedMath 2024, 4(1), 197-210; https://doi.org/10.3390/appliedmath4010010 - 04 Feb 2024
Abstract
►▼
Show Figures
Radiotherapy can differentially affect the phases of the cell cycle, possibly enhancing suppression of tumor growth, if cells are synchronized in a specific phase. A model is designed to replicate experiments that synchronize cells in the S phase using gemcitabine before radiation at
[...] Read more.
Radiotherapy can differentially affect the phases of the cell cycle, possibly enhancing suppression of tumor growth, if cells are synchronized in a specific phase. A model is designed to replicate experiments that synchronize cells in the S phase using gemcitabine before radiation at various doses, with the goal of quantifying this effect. The model is used to simulate a clinical trial with a cohort of 100 individuals receiving only radiation and another cohort of 100 individuals receiving radiation after cell synchronization. The simulations offered in this study support the statement that, at suitably high levels of radiation, synchronizing melanoma cells with gemcitabine before treatment substantially reduces the final tumor size. The improvement is statistically significant, and the effect size is noticeable, with the near suppression of growth at 8 Gray and 92% synchronization.
Full article
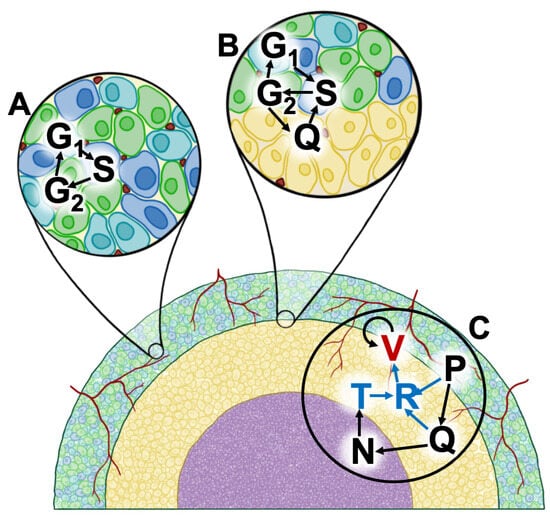
Figure 1
Open AccessArticle
A Model of Hepatitis B Viral Dynamics with Delays
by
Benito Chen-Charpentier
AppliedMath 2024, 4(1), 182-196; https://doi.org/10.3390/appliedmath4010009 - 01 Feb 2024
Cited by 1
Abstract
►▼
Show Figures
Hepatitis B is a liver disease caused by the human hepatitis B virus (HBV). Mathematical models help further the understanding of the processes involved and help make predictions. The basic reproduction number,
Hepatitis B is a liver disease caused by the human hepatitis B virus (HBV). Mathematical models help further the understanding of the processes involved and help make predictions. The basic reproduction number,
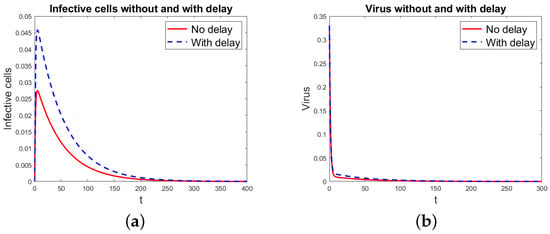
Figure 1
Highly Accessed Articles
Latest Books
E-Mail Alert
News
Topics

Conferences
Special Issues
Special Issue in
AppliedMath
Contemporary Iterative Methods with Applications in Applied Sciences
Guest Editors: Jai Prakash Jaiswal, Juan Ramón Torregrosa SánchezDeadline: 30 April 2024
Special Issue in
AppliedMath
Application of Machine Learning and Deep Learning Methods in Science
Guest Editors: Alexander Ayriyan, Vladimir Korenkov, Gennady OsoskovDeadline: 30 June 2024
Special Issue in
AppliedMath
Optimization and Machine Learning
Guest Editor: Yu ChenDeadline: 30 August 2024
Special Issue in
AppliedMath
Mathematical Perspectives on Quantum Computing and Communication
Guest Editors: Artur Czerwinski, Xiangji CaiDeadline: 31 October 2024




