Investigation of the Impact of High Concentration LiTFSI Electrolytes on Silicon Anodes with Reactive Force Field Simulations
Abstract
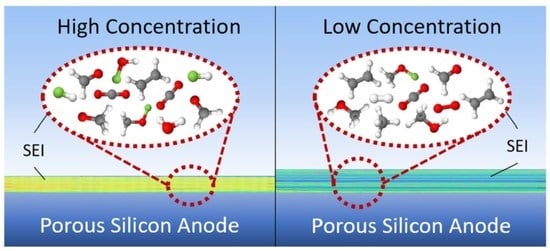
:1. Introduction
2. Materials and Methods
2.1. Theory
2.1.1. The ReaxFF Reactive Force Field
2.1.2. Evolutionary Algorithms
2.1.3. Force Field Parametrization
2.1.4. Molecular Dynamics Simulations
2.1.5. Preparation of Porous Silicon Anode
2.1.6. Electrochemical Characterization
2.1.7. Postmortem Characterization
3. Results
3.1. Reactive Force Field Simulation Results
3.1.1. Force Field Parametrization
- (1)
- ReaxFF, especially when parameterized for such a large collection of elements as conducted here, usually does not have the ability to reproduce whole potential energy surfaces with chemical accuracy. The aim is rather to obtain the correct relative activation barriers and structural parameters in order to make fast and qualitative simulations of complex reaction networks and alternative reaction paths accessible. In fact, the level of agreement achieved here is on par with typical ReaxFF fittings published in the literature.
- (2)
- Only a small subset of the important parameters was provided for optimization. All element-specific parameters and all bond parameters besides those for the S–Si bond were kept fixed. The reason for this is that those global parameters have a strong influence on any chemical situation that might occur during the simulation. Much better results regarding the present training set could be achieved if more parameters are released for optimization. Then, however, the large landscape of chemistry considering the reactions of DOL with TFSI, and products containing F, S, and N atoms, etc., would have been altered as well. A huge training set covering the information and references to all these possible reactions must be provided if this should be conducted.
3.1.2. Element Distributions
3.1.3. Bond Abundancies
3.1.4. Bond Distributions
3.1.5. Molecule Abundancies and Distributions
3.1.6. Reaction Mechanisms
3.2. Experimental Verification
3.2.1. Electrochemical Characterization
3.2.2. Post-Mortem Investigation
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Krause, A.; Dörfler, S.; Piwko, M.; Wisser, F.M.; Jaumann, T.; Ahrens, E.; Giebeler, L.; Althues, H.; Schädlich, S.; Grothe, J.; et al. High Area Capacity Lithium-Sulfur Full-Cell Battery with Prelithiatied Silicon Nanowire-Carbon Anodes for Long Cycling Stability. Sci. Rep. 2016, 6, 27982. [Google Scholar] [CrossRef]
- Ye, R.; Bell, J.; Patino, D.; Ahmed, K.; Ozkan, M.; Ozkan, C.S. Advanced Sulfur-Silicon Full Cell Architecture for Lithium Ion Batteries. Sci. Rep. 2017, 7, 17264. [Google Scholar] [CrossRef]
- Shen, C.; Ge, M.; Zhang, A.; Fang, X.; Liu, Y.; Rong, J.; Zhou, C. Silicon(lithiated)-Sulfur Full Cells with Porous Silicon Anode Shielded by Nafion Against Polysulfides to Achieve High Capacity and Energy Density. Nano Energy 2016, 19, 68–77. [Google Scholar] [CrossRef]
- Gao, J.; Lowe, M.A.; Kiya, Y.; Abruña, H.D. Effects of Liquid Electrolytes on the Charge/Discharge Performance of Rechargeable Lithium/Sulfur Batteries: Electrochemical and in-Situ X-ray Absorption Spectroscopic Studies. J. Phys. Chem. C 2011, 115, 25132–25137. [Google Scholar] [CrossRef]
- Watanabe, M.; Thomas, M.L.; Zhang, S.; Ueno, K.; Yasuda, T.; Dokko, K. Application of Ionic Liquids to Energy Storage and Conversion Materials and Devices. Chem. Rev. 2017, 117, 7190–7239. [Google Scholar] [CrossRef] [PubMed]
- Yamada, Y.; Furukawa, K.; Sodeyama, K.; Kikuchi, K.; Yaegashi, M.; Tateyama, Y.; Yamada, A. Unusual Stability of Acetonitrile-Based Superconcentrated Electrolytes for Fast-Charging Lithium-Ion Batteries. J. Am. Chem. Soc. 2014, 136, 5039–5046. [Google Scholar] [CrossRef] [PubMed]
- Yamada, Y.; Yamada, A. Review—Superconcentrated Electrolytes for Lithium Batteries. J. Electrochem. Soc. 2015, 162, A2406–A2423. [Google Scholar] [CrossRef]
- Kim, K.; Ma, H.; Park, S.; Choi, N.S. Electrolyte-Additive-Driven Interfacial Engineering for High-Capacity Electrodes in Lithium-Ion Batteries: Promises and Challenges. ACS Energy Lett. 2020, 5, 1537–1553. [Google Scholar] [CrossRef]
- Zhang, Y.; Du, N.; Yang, D. Designing superior solid electrolyte interfaces on silicon anodes for high-performance lithium-ion batteries. Nanoscale 2019, 11, 19086–19104. [Google Scholar] [CrossRef]
- Jung, S.C.; Choi, J.W.; Han, Y.K. Anisotropic Volume Expansion of Crystalline Silicon during Electrochemical Lithium Insertion: An Atomic Level Rationale. Nano Lett. 2012, 12, 5342–5347. [Google Scholar] [CrossRef]
- Dai, F.; Yi, R.; Yang, H.; Zhao, Y.; Luo, L.; Gordin, M.L.; Sohn, H.; Chen, S.; Wang, C.; Zhang, S.; et al. Minimized Volume Expansion in Hierarchical Porous Silicon upon Lithiation. ACS Appl. Mater. Interfaces 2019, 11, 13257–13263. [Google Scholar] [CrossRef] [PubMed]
- Schmidt, H.; Jerliu, B.; Hüger, E.; Stahn, J. Volume expansion of amorphous silicon electrodes during potentiostatic lithiation of Li-ion batteries. Electrochem. Commun. 2020, 115, 106738. [Google Scholar] [CrossRef]
- Ge, M.; Cao, C.; Biesold, G.M.; Sewell, C.D.; Hao, S.M.; Huang, J.; Zhang, W.; Lai, Y.; Lin, Z. Recent Advances in Silicon-Based Electrodes: From Fundamental Research toward Practical Applications. Adv. Mater. 2021, 33, 2004577. [Google Scholar] [CrossRef] [PubMed]
- Feng, K.; Li, M.; Liu, W.; Kashkooli, A.G.; Xiao, X.; Cai, M.; Chen, Z. Silicon-Based Anodes for Lithium-Ion Batteries: From Fundamentals to Practical Applications. Small 2018, 14, 1702737. [Google Scholar] [CrossRef]
- Tokranov, A.; Kumar, R.; Li, C.; Minne, S.; Xiao, X.; Sheldon, B.W. Control and Optimization of the Electrochemical and Mechanical Properties of the Solid Electrolyte Interphase on Silicon Electrodes in Lithium Ion Batteries. Adv. Energy Mater. 2016, 6, 1502302. [Google Scholar] [CrossRef]
- Park, J.W.; Ueno, K.; Tachikawa, N.; Dokko, K.; Watanabe, M. Ionic liquid electrolytes for lithium-sulfur batteries. J. Phys. Chem. C 2013, 117, 20531–20541. [Google Scholar] [CrossRef]
- Dokko, K.; Tachikawa, N.; Yamauchi, K.; Tsuchiya, M.; Yamazaki, A.; Takashima, E.; Park, J.W.; Ueno, K.; Seki, S.; Serizawa, N.; et al. Solvate Ionic Liquid Electrolyte for Li-S Batteries. J. Electrochem. Soc. 2013, 160, A1304–A1310. [Google Scholar] [CrossRef]
- Zeng, Z.; Murugesan, V.; Han, K.S.; Jiang, X.; Cao, Y.; Xiao, L.; Ai, X.; Yang, H.; Zhang, J.G.; Sushko, M.L.; et al. Non-Flammable Electrolytes with High Salt-to-Solvent Ratios for Li-ion and Li-metal Batteries. Nat. Energy 2018, 3, 674–681. [Google Scholar] [CrossRef]
- Suo, L.; Hu, Y.S.; Li, H.; Armand, M.; Chen, L. A New Class of Solvent-in-Salt Electrolyte for High-Energy Rechargeable Metallic Lithium Batteries. Nat. Commun. 2013, 4, 1481. [Google Scholar] [CrossRef]
- Wang, M.; Huai, L.; Hu, G.; Yang, S.; Ren, F.; Wang, S.; Zhang, Z.; Chen, Z.; Peng, Z.; Shen, C.; et al. Effect of LiFSI Concentrations to Form Thickness- and Modulus-Controlled SEI Layers on Lithium Metal Anodes. J. Phys. Chem. C 2018, 122, 9825–9834. [Google Scholar] [CrossRef]
- Becke, A.D. Density-functional thermochemistry. III. The role of exact exchange. J. Chem. Phys. 1993, 98, 5648–5652. [Google Scholar] [CrossRef]
- Stephens, P.J.; Devlin, F.J.; Chabalowski, C.F.; Frisch, M.J. Ab Initio Calculation of Vibrational Absorption and Circular Dichroism Spectra Using Density Functional Force Fields. J. Phys. Chem. 1994, 98, 11623–11627. [Google Scholar] [CrossRef]
- Adamo, C.; Barone, V. Toward reliable density functional methods without adjustable parameters: The PBE0 model. J. Chem. Phys. 1999, 110, 6158. [Google Scholar] [CrossRef]
- Ganesh, P.; Kent, P.R.C.; Jiang, D. Solid–Electrolyte Interphase Formation and Electrolyte Reduction at Li-Ion Battery Graphite Anodes: Insights from First-Principles Molecular Dynamics. J. Phys. Chem. C 2012, 116, 24476–24481. [Google Scholar] [CrossRef]
- Martinez de la Hoz, J.M.; Leung, K.; Balbuena, P.B. Reduction Mechanisms of Ethylene Carbonate on Si Anodes of Lithium-Ion Batteries: Effects of Degree of Lithiation and Nature of Exposed Surface. ACS Appl. Mater. Interfaces 2013, 5, 13457–13465. [Google Scholar] [CrossRef]
- Soto, F.A.; Martinez de la Hoz, J.M.; Seminario, J.M.; Balbuena, P.B. Modeling solid electrolyte interfacial phenomena in silicon anodes. Curr. Opin. Chem. Eng. 2016, 13, 179–185. [Google Scholar] [CrossRef]
- Damm, W.; Frontera, A.; Tirado-Rives, J.; Jorgensen, W.J. OPLS all-atom force field for carbohydrates. J. Comput. Chem. 1997, 18, 1955–1970. [Google Scholar] [CrossRef]
- Doherty, B.; Zhong, X.; Gathiaka, S.; Li, B.; Acevedo, O. Revisiting OPLS Force Field Parameters for Ionic Liquid Simulations. J. Chem. Theory Comput. 2017, 13, 6131–6145. [Google Scholar] [CrossRef]
- Van Duin, A.C.T.; Dasgupta, S.; Lorant, F.; Goddard, W.A., III. ReaxFF: A Reactive Force Field for Hydrocarbons. J. Phys. Chem. A 2001, 105, 9396–9409. [Google Scholar] [CrossRef]
- Han, Y.; Joang, D.; Zhang, J.; Li, W.; Gan, Z.; Gu, J. Development, applications and challenges of ReaxFF reactive force field in molecular simulations. Front. Chem. Sci. Eng. 2016, 10, 16–38. [Google Scholar] [CrossRef]
- Senftle, T.P.; Hong, S.; Islam, M.M.; Kylasa, S.B.; Zheng, Y.; Shin, Y.K.; Junkermeier, C.; Engel-Herbert, R.; Janik, M.J.; Aktulga, H.M.; et al. The ReaxFF reactive force-field: Development, applications and future directions. NPJ Comp. Mater. 2016, 2, 15011. [Google Scholar] [CrossRef]
- Bai, C.; Liu, L.; Sun, H. Molecular Dynamics Simulations of Methanol to Olefin Reactions in HZSM-5 Zeolite Using a ReaxFF Force Field. J. Phys. Chem. C 2012, 116, 7029–7039. [Google Scholar] [CrossRef]
- Fogarty, J.C.; Aktulga, H.M.; Grama, A.Y.; van Duin, A.C.T. A reactive molecular dynamics simulation of the silica-water interface. J. Chem. Phys. 2010, 132, 174704. [Google Scholar] [CrossRef] [PubMed]
- Kulkarni, A.D.; Truhlar, D.G.; Srinivasan, S.G.; van Duin, A.C.T.; Norman, P.; Schwarzentruber, T.E. Oxygen Interactions with Silica Surfaces: Coupled Cluster and Density Functional Investigation and the Development of a New ReaxFF Potential. J. Phys. Chem. C 2013, 117, 258–269. [Google Scholar] [CrossRef]
- Soria, F.A.; Zhang, W.; Paredes-Olivera, P.A.; van Duin, A.C.T.; Patrito, E.M. Si/C/H ReaxFF Reactive Potential for Silicon Surfaces Grafted with Organic Molecules. J. Phys. Chem. C 2018, 122, 23515–23527. [Google Scholar] [CrossRef]
- Yue, D.C.; Ma, T.B.; Hu, Y.Z.; Yeon, J.; van Duin, A.C.T.; Wang, H.; Luo, J. Tribochemistry of Phosphoric Acid Sheared between Quartz Surfaces: A Reactive Molecular Dynamics Study. J. Phys. Chem. C 2013, 117, 25604–25614. [Google Scholar] [CrossRef]
- Shi, Z.; Zhou, J.; Li, R. Application of Reaction Force Field Molecular Dynamics in Lithium Batteries. Front. Chem. 2021, 8, 15011. [Google Scholar] [CrossRef]
- Han, S.S.; van Duin, A.C.T.; Goddard, W.A., III; Lee, H.M. Optimization and Application of Lithium Parameters for the Reactive Force Field, ReaxFF. J. Phys. Chem. A 2005, 109, 4575–4582. [Google Scholar] [CrossRef]
- Raju, M.; Ganesh, P.; Kent, P.C.R.; van Duin, A.C.T. Reactive Force Field Study of Li/C Systems for Electrical Energy Storage. J. Chem. Theory Comput. 2015, 11, 2156–2166. [Google Scholar] [CrossRef]
- Cui, J.; Zheng, F.; Wu, S.; Zhu, Z.Z. ReaxFF Molecular Dynamics Simulations on Silicon Suboxide as Anode Material for Lithium-Ion Batteries. J. Electrochem. Soc. 2020, 167, 020547. [Google Scholar] [CrossRef]
- Ostadhossein, A.; Kim, S.Y.; Cubuk, E.D.; Qi, Y.; van Duin, A.C.T. Atomic Insight into the Lithium Storage and Diffusion Mechanism of SiO2/Al2O3 Electrodes of Lithium Ion Batteries: ReaxFF Reactive Force Field Modeling. J. Phys. Chem. A 2016, 120, 2114–2127. [Google Scholar] [CrossRef] [PubMed]
- Kim, S.P.; van Duin, A.C.T.; Shenoy, V.B. Effect of electrolytes on the structure and evolution of the solid electrolyte interphase (SEI) in Li-ion batteries: A molecular dynamics study. J. Power Sources 2011, 196, 8590–8597. [Google Scholar] [CrossRef]
- Gissinger, J.R.; Jensen, B.D.; Wise, K.E. REACTER: A Heuristic Method for Reactive Molecular Dynamics. Macromolecules 2020, 53, 9953–9961. [Google Scholar] [CrossRef]
- Alzate-Vargas, L.; Blau, S.M.; Spotte-Smith, E.W.C.; Allu, S.; Persson, K.A.; Fattebert, J.-L. Insight into SEI Growth in Li-Ion Batteries using Molecular Dynamics and Accelerated Chemical Reactions. J. Phys. Chem. C 2021, 125, 18588–18596. [Google Scholar] [CrossRef]
- Nöhren, S.; Quiroga-Gonzalez, E.; Carstensen, J.; Föll, H. Electrochemical Fabrication and Characterization of Silicon Microwire Anodes for Li Ion Batteries. J. Electrochem. Soc. 2015, 163, A373. [Google Scholar] [CrossRef]
- Hansen, S.; Shree, S.; Neubüser, G.; Carstensen, J.; Kienle, L.; Adelung, R. Corset-like solid electrolyte interface for fast charging of silicon wire anodes. J. Power Sources 2018, 381, 8–17. [Google Scholar] [CrossRef]
- Hansen, S.; Quiroga-Gonzalez, E.; Carstensen, J.; Föll, H. Size-dependent cyclic voltammetry study of silicon microwire anodes for lithium ion batteries. Electrochim. Acta 2016, 217, 283–291. [Google Scholar] [CrossRef]
- Sakabe, J.; Ohta, N.; Ohnishi, T.; Mitsuishi, K.; Takada, K. Porous amorphous silicon film anodes for high-capacity and stable all-solid-state lithium batteries. Commun. Chem. 2018, 1, 24. [Google Scholar] [CrossRef]
- Cangaz, S.; Hippauf, F.; Reuter, R.S.; Doerfler, S.; Abendroth, T.; Althues, H.; Kaskel, S. Enabling High-Energy Solid-State Batteries with Stable Anode Interphase by the Use of Columnar Silicon Anodes. Adv. Energy Mater. 2020, 10, 2001320. [Google Scholar] [CrossRef]
- Younesi, R.; Veith, G.M.; Johansson, P.; Edström, K.; Vegge, T. Lithium salts for advanced lithium batteries: Li–metal, Li–O2, and Li–S. Energy Environ. Sci. 2015, 8, 1905–1922. [Google Scholar] [CrossRef] [Green Version]
- Aurbach, D.; Zaban, A.; Gofer, Y.; Ely, Y.E.; Weissman, I.; Chusid, O.; Abramson, O. Recent studies of the lithium-liquid electrolyte interface Electrochemical, morphological and spectral studies of a few important systems. J. Power Sources 1995, 54, 76–84. [Google Scholar] [CrossRef]
- Menne, S.; Pires, J.; Anouti, M.; Balducci, A. Protic ionic liquids as electrolytes for lithium-ion batteries. Electrochem. Comm. 2013, 31, 39–41. [Google Scholar] [CrossRef]
- Chenoweth, K.; van Duin, A.C.T.; Goddard, W.A. ReaxFF Reactive Force Field for Molecular Dynamics Simulations of Hydrocarbon Oxidation. J. Phys. Chem. A 2008, 112, 1040–1053. [Google Scholar] [CrossRef] [PubMed]
- Mortier, W.J.; Ghosh, S.K.; Shankar, S. Electronegativity-equalization method for the calculation of atomic charges in molecules. J. Am. Chem. Soc. 1986, 108, 4315–4320. [Google Scholar] [CrossRef]
- Hartke, B. Global Optimization. WIREs Comput. Mol. Sci. 2011, 1, 879–887. [Google Scholar] [CrossRef]
- Dittner, M.; Müller, J.; Aktulga, H.M.; Hartke, B. Efficient Global Optimization of Reactive Force Field Parameters. J. Comput. Chem. 2015, 36, 1550–1561. [Google Scholar] [CrossRef] [PubMed]
- Weise, T. Global Optimization Algorithms—Theory and Application. Available online: http://www.it-weise.de/projects/book.pdf (accessed on 7 September 2022).
- Hartke, B. Non-deterministic global structure optimization: An introductory tutorial. In Reviews in Computational Chemistry; Parrill, A., Lipkowitz, K., Eds.; Wiley e-Books: Hoboken, NJ, USA, 2022; Volume 32. [Google Scholar]
- Liu, Y.; Yu, P.; Wu, Y.; Yang, H.; Xie, M.; Huai, L.; Giddard, W.A.; Cheng, T. The DFT-ReaxFF Hybrid Reactive Dynamics Method with Application to the Reductive Decomposition Reaction of the TFSI and DOL Electrolyte at a Lithium−Metal Anode Surface. J. Phys. Chem. Lett. 2021, 12, 1300–1306. [Google Scholar] [CrossRef]
- Yun, K.S.; Pai, S.J.; Yeo, B.C.; Lee, K.R.; Kim, S.J.; Han, S.S. Simulation Protocol for Prediction of a Solid-Electrolyte Interphase on the Silicon-based Anodes of a Lithium-Ion Battery: ReaxFF Reactive Force Field. J. Phys. Chem. Lett. 2017, 8, 2812–2818. [Google Scholar] [CrossRef]
- Wang, Y.; Shi, Y.; Sun, Q.; Lu, K.; Kubo, M.; Xu, J. Development of a Transferable ReaxFF Parameter Set for Carbon- and Silicon-Based Solid Systems. J. Phys. Chem. C 2020, 124, 10007–10015. [Google Scholar] [CrossRef]
- McLean, A.D.; Chandler, G.S. Contracted Gaussian-basis sets for molecular calculations. 1. 2nd row atoms, Z = 11–18. J. Chem. Phys. 1980, 72, 5639–5648. [Google Scholar] [CrossRef]
- Raghavachari, K.; Binkley, J.S.; Seeger, R.; Pople, J.A. Self-Consistent Molecular Orbital Methods. 20. Basis set for correlated wave-functions. J. Chem. Phys. 1980, 72, 650–654. [Google Scholar]
- Dieterich, J.M.; Hartke, B. OGOLEM: Global cluster structure optimisation for arbitrary mixtures of flexible molecules. A multiscaling, object-oriented approach. Mol. Phys. 2010, 108, 279–291. [Google Scholar] [CrossRef]
- OGOLEM.ORG: Framework for GA-Based Global Optimization. Available online: https://www.ogolem.org (accessed on 10 November 2022).
- Plimpton, S. Fast Parallel Algorithms for Short-Range Molecular Dynamics. J. Comp. Phys. 1995, 117, 1–19. [Google Scholar] [CrossRef]
- Thompson, A.P.; Aktulga, H.M.; Berger, R.; Bolintineanu, D.S.; Brown, W.M.; Crozier, P.S.; in’t Veld, P.J.; Kohlmeyer, A.; Moore, S.G.; Nguyen, T.D.; et al. LAMMPS—A flexible simulation tool for particle-based materials modeling at the atomic, meso, and continuum scales. Comp. Phys. Comm. 2022, 271, 108171. [Google Scholar] [CrossRef]
- LAMMPS. Available online: https://www.lammps.org (accessed on 8 September 2022).
- Aktulga, H.M.; Fogarty, J.C.; Pandit, S.A.; Grama, A.Y. Parallel reactive molecular dynamics: Numerical methods and algorithmic techniques. Parallel Comput. 2012, 38, 245–259. [Google Scholar] [CrossRef]
- Nose, S. A unified formulation of the constant temperature molecular dynamics methods. J. Chem. Phys. 1984, 81, 511. [Google Scholar] [CrossRef]
- O’Boyle, N.M.; Banck, M.; James, C.A.; Morley, C.; Vandermeersch, T.; Hutchinson, G.R. Open Babel: An open chemical toolbox. J. Chemoinform. 2011, 3, 33. [Google Scholar] [CrossRef]
- Weininger, D. SMILES, a chemical language and information system. 1. Introduction to methodology and encoding rules. J. Chem. Inf. Comput. Sci. 1988, 28, 31–36. [Google Scholar] [CrossRef]
- Chen, X.; Hou, T.-Z.; Li, B.; Yan, C.; Zhu, L.; Guan, C.; Cheng, X.-B.; Peng, H.-J.; Huang, J.-Q.; Zhang, Q. Towards stable lithium-sulfur batteries: Mechanistic insights into electrolyte decomposition on lithium metal anode. Energy Storage Mater. 2017, 8, 194–201. [Google Scholar] [CrossRef]
- Gao, H.; Xiao, L.; Plümel, I.; Xu, G.L.; Yang, R.; Zuo, X.; Liu, Y.; Schulz, C.; Wiggers, H.; Amine, K.; et al. Parasitic Reactions in Nanosized Silicon Anodes for Lithium-Ion Batteries. Nano Lett. 2017, 17, 1512–1519. [Google Scholar] [CrossRef]
- Arreaga-Salas, D.E.; Sra, A.K.; Roodenko, K.; Chabal, Y.J.; Hinkle, C.L. Progression of Solid Electrolyte Interphase Formation on Hydrogenated Amorphous Silicon Anodes for Lithium-Ion Batteries. J. Phys. Chem. C 2012, 116, 9072–9077. [Google Scholar] [CrossRef]
- Kitz, P.G.; Novak, P.; Berg, E.J. Influence of Water Contamination on the SEI Formation in Li-Ion Cells: An Operando EQCM-D Study. ACS Appl. Mater. Interfaces 2022, 12, 15934–15942. [Google Scholar] [CrossRef] [PubMed]
- Chang, Z.H.; Wang, J.T.; Wu, Z.H.; Gao, M.; Wu, S.J. The Electrochemical Performance of Silicon Nanoparticles in Concentrated Electrolyte. ChemSusChem 2018, 2, 1787–1796. [Google Scholar] [CrossRef]
- Etacheri, V.; Haik, O.; Goffer, Y.; Roberts, G.A.; Stefan, I.C.; Fasching, R.; Aurbach, D. Effect of Fluoroethylene Carbonate (FEC) on the Performance and Surface Chemistry of Si-Nanowire Li-Ion Battery Anodes. Langmuir 2012, 28, 965–976. [Google Scholar] [CrossRef] [PubMed]
- Jaumann, T.; Balach, J.; Klose, M.; Oswald, S.; Eckert, J.; Giebeler, L. Role of 1,3-Dioxolane and LiNO3 Addition on the Long Term Stability of Nanostructured Silicon/Carbon Anodes for Rechargeable Lithium Batteries. J. Electrochem. Soc. 2016, 163, A557–A564. [Google Scholar] [CrossRef]
- Aurbach, D.; Pollak, E.; Elazari, R.; Salitra, G.; Kelley, C.S.; Afinito, J. On the Surface Chemical Aspects of Very High Energy Density, Rechargeable Li–Sulfur Batteries. J. Electrochem. Soc. 2009, 156, A694–A702. [Google Scholar] [CrossRef]
- Peled, E.; Menkin, S. Review—SEI: Past, Present and Future. J. Electrochem. Soc. 2017, 164, A1703. [Google Scholar] [CrossRef]
- Verma, P.; Maire, P.; Novak, P. A review of the features and analyses of the solid electrolyte interphase in Li-ion batteries. Electrochim. Acta 2010, 55, 6332–6341. [Google Scholar] [CrossRef]
- Ravikumar, B.; Mynam, M.; Rai, B. Effect of Salt Concentration on Properties of Lithium Ion Battery Electrolytes: A Molecular Dynamics Study. J. Phys. Chem. C 2018, 122, 8173–8181. [Google Scholar] [CrossRef]
- Cao, C.; Abate, I.I.; Sivonxay, E.; Shyam, B.; Jia, C.; Moritz, B.; Devereaux, T.P.; Persson, K.A.; Steinrück, H.G.; Toney, M.F. Solid Electrolyte Interphase on Native Oxide-Terminated Silicon Anodes for Li-Ion Batteries. Joule 2019, 3, 762–781. [Google Scholar] [CrossRef]
- Yoon, T.; Chapman, N.; Seo, D.M.; Lucht, B.L. Lithium Salt Effects on Silicon Electrode Performance and Solid Electrolyte Interphase (SEI) Structure, Role of Solution Structure on SEI Formation. J. Electrochem. Soc. 2017, 164, A2082–A2088. [Google Scholar] [CrossRef] [Green Version]
- Nilsson, V.; Younesi, R.; Brandell, D.; Edström, K.; Johansson, P. Critical evaluation of the stability of highly concentrated LiTFSI—Acetonitrile electrolytes vs. graphite, lithium metal and LiFePO4 electrodes. J. Power Sources 2018, 384, 334–341. [Google Scholar] [CrossRef]




















| S–Si | Si–Si–S | Si–S–Si | H–Si–S | Si–S–H | Si–S–S |
| Si–S–O | Si–O–S | S–Si–F | Si–S–N | C–N–S | C–Si–F |
| F–S–F | Si–N–S | F–N–N | F–N–S | F–S–S | F–N–F |
| F–C–N | S–Si–N | F–O–F | O–O–F |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cavers, H.; Steffen, J.; Gogoi, N.; Adelung, R.; Hartke, B.; Hansen, S. Investigation of the Impact of High Concentration LiTFSI Electrolytes on Silicon Anodes with Reactive Force Field Simulations. Liquids 2023, 3, 132-158. https://doi.org/10.3390/liquids3010011
Cavers H, Steffen J, Gogoi N, Adelung R, Hartke B, Hansen S. Investigation of the Impact of High Concentration LiTFSI Electrolytes on Silicon Anodes with Reactive Force Field Simulations. Liquids. 2023; 3(1):132-158. https://doi.org/10.3390/liquids3010011
Chicago/Turabian StyleCavers, Heather, Julien Steffen, Neeha Gogoi, Rainer Adelung, Bernd Hartke, and Sandra Hansen. 2023. "Investigation of the Impact of High Concentration LiTFSI Electrolytes on Silicon Anodes with Reactive Force Field Simulations" Liquids 3, no. 1: 132-158. https://doi.org/10.3390/liquids3010011