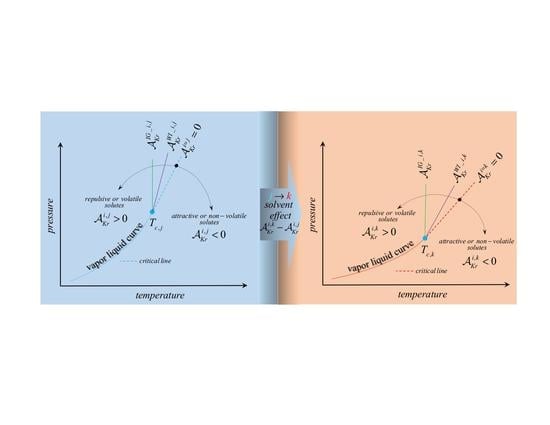
1. Introduction
The Krichevskii parameter defines a finite-size quantity as the limiting critical value of the isothermal-isochoric rate of change of the system’s pressure caused by the mutation (aka alchemical transformation) of an
solvent particle into an
solute species, in an otherwise pure solvent, i.e.,
[
1]. Even though
is a finite quantity, its magnitude and sign are the result of the underlying solute-solvent intermolecular interaction asymmetry [
2,
3,
4], where the developing pressure perturbation propagates across the entire system given that the solvent’s correlation length diverges at criticality [
5,
6].
The interest on the Krichevskii parameter has grown immensely since its inception [
2], in part, because it has become a key quantity in the description and/or correlation of the thermodynamic behavior of dilute solutions, especially for non-electrolyte aqueous systems [
7,
8,
9,
10,
11,
12,
13]. Its relevance has generated the urgency for experimental approaches to its determination, involving a variety of methodologies as discussed elsewhere [
14,
15,
16]. Unfortunately, the accumulated tabulations of Krichevskii parameters, especially involving light and heavy water as well as carbon dioxide as solvents [
15,
16,
17,
18,
19,
20,
21], involve significantly large uncertainties [
4,
14,
22], a condition that hinders our ability to make accurate interpretations [
23].
On the one hand, this (uncertainty) issue becomes exacerbated when studying the solvation of gases in isotopomers of a solvent such as light and heavy water, where the isotopic effect on the Krichevskii parameters given by their “brute-force” difference
, is typically more than an order of magnitude smaller than the observed uncertainties of
for the individual
isotopic form of the solvent [
24]. In other words, this is the undesirable situation involving typically small differences between two large quantities exhibiting significant uncertainties whose outcome is substantially smaller than its combined uncertainty.
On the other hand, it appears appealing to have a direct route for the assessment of the effect of the type of solvent on the resulting Krichevskii parameter based solely on the contrasting solvation characteristic of the solute in the desired solvent, relative to that of a reference solvent, i.e., in terms of the distinctive standard solvation Gibbs free energies of the solute and the Krichevskii parameters of an ideal gas solute in the pair of solvents. Indeed, the matter we would like to address here can be encapsulated in the following two questions: (a) how could we determine the Krichevskii parameter of an solute in a solvent, , when we accurately know not only the solvation behavior of the solute in a solvent at ambient conditions but also, its Krichevskii parameter ?, and (b) how could we determine directly the change in the Krichevskii parameter of an solute, , when we replace the solvent with a solvent and simultaneously know accurately the solvation behavior at ambient conditions of the solute in both solvents?
In this work, we suggest an approach to answer these questions, by establishing routes for the determination of the isotopic effect on the Krichevskii parameter of a solute, i.e., when the solvents are isotopomers, and then, by generalizing the approach to any pair of solvents. For that purpose, in
Section 2, we provide the thermodynamic foundations underlying the isobaric-isothermal transfer of an
solute from the
solvent phase to the
solvent phase, as characterized by the transfer Gibbs free energy of the dilute solute. Therefore, we draw the link between the standard solvation Gibbs free energy of the
solute in the pair of solvent environments,
, and the resulting Krichevskii parameters,
. Then, we identify the aqueous systems of interest and the sources of experimental data in
Section 3, discuss the fundamentally based linear behavior of the
representation in terms of the solute-solvent intermolecular interaction asymmetry, compare the resulting
solvent effect on the Krichevskii parameters of selected aqueous gases, and consequently, interpret two emblematic cases of aqueous solutions involving either an ideal gas solute or an
solute behaving as the solvating
isotopic form of water. To complete the development, in
Section 4 we provide a novel microstructural interpretation of the solvent effect according to a rigorous characterization of the critical solvation in terms of a finite unambiguous structure making/breaking parameter
, and identify some relevant observations. Finally, we close the manuscript with some additional remarks and outlook.
3. Experimental Evidence of the Solvent H/D−Isotope Substitution Effects and Solvation Interpretation
While the described molecular-based approach to the solvent effect on the Krichevskii parameter of an
solute applies to any type of solvent, here we focus our attention on the special case of
isotopic substituted aqueous solvents, i.e., water isotopomers. The rationale for this choice is twofold: (
a) these near-critical aqueous environments are frequently found in electric power generation and pose significantly challenging to study experimentally [
34,
35,
36], and (
b) the small magnitude of the
effect on the thermodynamic properties of the aqueous solvent makes the alluded brute-force subtraction approach unreliable as a result of the large uncertainties involved in the individual near-critical quantities (vide infra). As a reference, and to be more precise, the typical uncertainties of the experimental Krichevskii parameters might reach
and even higher depending on the evaluation method [
14,
16] while the
effect on the Krichevskii parameters might amount to a small fraction of the alluded uncertainty.
Typically, the hydration (solvation) behavior of a solute is analyzed in terms of standard thermodynamic quantities and their relation to the transfer process of a solute from the ideal gas phase to its standard state in solution. In fact, we have two alternative paths toward the determination of an
solute standard state property
namely, through its standard state dissolution quantity
or its standard state hydration (solvation) counterpart,
where
stands for and ideal gas phase, the superscripts
describe environments at infinite dilution and pure component, respectively, while
[
37]. Here, we are focusing on
, the partial molar Gibbs free energy of the
solute at infinite dilution under a diversity of manifestations, including the standard hydration (solvation) Gibbs free energies
[
38], Ben-Naim’s solvation Gibbs free energy
[
29], and the standard Gibbs free energy of solution
[
39,
40], whose meanings and their interrelations are provided in
Appendix A.
3.1. Identity of the Aqueous Solute Species and the Sources of Their Experimental Data
The systems targeted here are aqueous solutions of gaseous solutes, where the aqueous environments are either light or heavy water, and the
solute species include simple and noble gases, as well as some halogen-substituted light hydrocarbons. In particular, the list of
solutes include
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
, and
. This selection is based on the availability of (either assumed or considered) reliable experimental data for either the Krichevskii parameters of the solutes in both light and heavy aqueous systems or their hydration and/or transfer Gibbs free energies. In fact, we invoked the study of the near-critical behavior of the Henry’s law constant and vapor-liquid distribution coefficient of several solutes in light and heavy water by Fernandez-Prini et al. [
24] complemented by available information on the Gibbs free energy of hydration of these gases in both aqueous environment as well as the their Gibbs free energy of transfer between light and heavy water [
39,
41,
42].
In
Table 1, we present the calculated Krichevskii parameters of the dissolved gases in light and heavy aqueous systems and the resulting standard Gibbs free energies of hydration from the regressions of Ref. [
24] as well as from solubility measurements from Refs. [
39,
41,
42] as explicitly indicated. In particular, in columns 2 and 3 of
Table 1, we reveal the Krichevskii parameters of the
solutes in light and heavy water as determined from the parameter
resulting from the regression of the solute distribution coefficients in Ref. [
24]. Moreover, in columns 4 and 5, we display the corresponding data for the Gibbs free energies of hydration derived from the regression of the Henry’s law constants in Ref. [
24], and complemented with those calculated from solubility measurements in Refs. [
39,
41,
42].
3.2. Brute-Force Difference Approach to the Solvent Effect on the Krichevskii Parameter of a Solute
The obvious first attempt to assess the solvent effect is the simple subtraction between the third and second columns of
Table 1 as illustrated in
Table 2, i.e.,
, where we also provide the quoted uncertainties from Ref. [
24]. It becomes immediately evident that we cannot expect reliable results for the solvent (and particularly, for the
isotopic substitution) effects from the corresponding values of the Krichevskii parameter of a solute because their subtraction will result in a magnification of the individual uncertainties [
43].
This contention is additionally supported by the analysis of the uncertainties associated with the determination of the Krichevskii parameters of an ideal gas solute in light and heavy water from the regression of their solute vapor–liquid distribution coefficients, systems for which we know the exact answer [
44]. This scenario suggests the need for an alternative approach to assess directly the underlying isotopic effect and avoid the unreliable brute-force subtraction method.
3.3. Required Solvation Properties in the Molecular-Based Approach to the Solvent H/D−Effect on the Krichevskii Parameter
For the implementation of the approach proposed in
Section 2.1 and
Section 2.2, we proceed with the calculation of the required hydration (solvation) properties as follows. Based on the data of
Table 1, we can determine the Gibbs free energy of transfer
, Equation (4), in terms of the hydration Gibbs free energy of the
solute in the two isotopic forms of the solvent,
Alternatively,
can be determined according to Ben-Naim’s scheme [
45], i.e.,
where
is given by the following difference of solvation quantities,
after invoking the relations derived in
Appendix A.
Moreover, we calculate the underlying solute-solvent intermolecular interaction asymmetry for the
solute,
, according to the expression [
46],
where
while the Gibbs free energy upon solution of the
solute in the
solvent,
, reads as follows,
with the subscript (
) emphasizing that we are dealing with either
or
as the solvent. Then, from the solubility measurements,
, we estimate the activity coefficient
according to [
47],
as a more accurate alternative to the conventional
relation used in (A13) of
Appendix A, so that
according to (A15) in
Appendix A. The resulting values from Equations (12) and (15) are given in
Table 3 below.
3.4. Resulting Linear Representation for the Krichevskii Parameter
After recalling that
defines the Krichevskii parameter of the
solute as an ideal gas in the
solute as an ideal gas in the solvent with
[
8,
32], and considering the critical conditions of the light [
48] and heavy water [
49,
50], we immediately find that
and
. Therefore, by invoking Equations (7) and (A4) as well as the corresponding residual chemical potentials
and
of the pure
solvent, we obtain the following linear representations for the Krichevskii parameter of an
solute in light and heavy water,
and,
where,
which is (A3) from
Appendix A, for
.
As we might have expected, the resulting linear hydration Gibbs free energy representations, Equations (19) and (20), exhibit slightly different slopes in their dependence on the relative (to that of the corresponding pure
solvent) hydration free energies. These expressions highlight the size of the resulting
isotopic substitution effect on the Krichevskii parameter of the solutes under investigation, i.e., such an effect is significantly smaller than the magnitude of the reported uncertainties of the individual Krichevskii parameters
and
[
24].
We have recently addressed the uncertainty issue according to a rigorous analysis of the behavior of the orthobaric-density dependence of the solute distribution coefficient of an ideal gas solute at infinite dilution,
, when the
solvent was light water [
23]. Moreover, we have illustrated how small experimental uncertainties of the solute distribution coefficient at high temperature can drastically affect the outcome of the regression, and consequently, the resulting effective Krichevskii parameter [
44]. Indeed, by analyzing the behavior of
when the
solvent was either light or heavy water, we found that there were no
isotopic effects on the orthobaric-density slope within the range of effective linearity as a consequence of the null solute-solvent interactions. However, as we replaced the ideal gas solute with a real gas (compare Figures 8 and 9 in Ref. [
44]), the range of effective linearity of the
when the
solvent was heavy water became narrower than that observed for the same solute in light water, i.e., a clear manifestation of the
isotopic effect associated with the non-zero solute-solvent interactions. Obviously, this feature imposes a stronger constraint on either the
range or its lowest
, where we could invoke the asymptotic orthobaric
effective linearity leading to the determination of the Krichevskii parameter. On the one hand, the closer
is to
, the better since it provides a more accurate representation of the asymptotic critical slope; on the other hand, the closeness of the chosen
to
is significantly constrained by the experimental challenges associated with highly compressible environments.
3.5. Link between the Solvent H/D−Effect on the Krichevskii Parameter and Solute–Solvent Intermolecular Interaction Asymmetries
Considering the nature of the aqueous systems under study, we can first invoke the following identity [
30],
where the superscript
identifies the liquid phase of the
solvent. Then, we introduce the accurate second-order composition representation for the partial molar excess free energy of an interacting solute, (see Appendix A of Ref. [
30] and Appendix B of Ref. [
46] for details while noting that the second-order expansion is unable to describe accurately the behavior of non-interacting solutes as discussed in Ref. [
51]) to find a link between the magnitude of the Henry’s law constant of an
solute and a precisely-defined molecular measure of solute-solvent intermolecular interaction asymmetry, i.e.,
where we have invoked Equations (15) and (16) to describe the infinite dilution activity coefficient
in Equation (22). Moreover, by introducing Equation (23) into Equation (7), we obtain a revealing linear dependence of the magnitude of the Krichevskii parameter of the
solute and the solute-solvent intermolecular interaction asymmetry,
, as follows,
with
. In other words, the Krichevskii parameter of an
solute in an
solvent,
, becomes described by a linear function of
with a slope
, whose ordinate at the origin becomes
. Therefore, according to Equations (7) and (24), the solvent effect on the Krichevskii parameter of an
solute defined as the difference of Krichevskii parameters between the two solvents,
, becomes
This equation suggests that
can be interpreted as a
prorated difference of the solute-solvent intermolecular interaction asymmetry function
, an observation that we will analyze below. In fact, we should note that the isothermal-isochoric residual chemical potential of the gaseous solutes at infinite dilution in aqueous solutions,
, exhibits a linear dependence with the corresponding solute-solvent intermolecular interaction asymmetry function
as illustrated in
Figure 2 when the
solvent is either light or heavy water at ambient conditions. We can also identify
at a hypothetical value of the solute-solvent intermolecular interaction asymmetry, i.e., one that differs from the theoretical
. The reason for this difference resides in the fact that, as demonstrated in Ref. [
51], the second-order expansion cannot provide an accurate description of the behavior of non-interacting solutes, i.e., it requires at least a six-order composition expansion. However, because the condition
also means that
, we can determine the hypothetical value of
so that
, where
comprises contributions from the first few infinite dilution composition derivatives of the
as indicated by Equation S5 in the Supplementary Information document of Ref. [
51].
Given the observed linearity in
Figure 2, and the definition of the Gibbs free energy of transfer, Equation (10) in the alternative form
, we also expect a
linearly dependent on the difference
. In fact, the quadratic-composition dependent
that describes accurately the
nonideal behavior of these solutes [
46] leads to
with
, while the condition
for an
solute translates into
and identified as the red dot in
Figure 3. Note also that, while the second-order composition approximation for
is not accurate for an
solute as indicated above, we can still identify the
solute in
Figure 3, given that Equation (4) becomes
for this solute.
According to the linear behaviors described above, we can alternatively express the solvent effect
in terms of the solvation Gibbs free energies
as follows,
where
identifies the solvation Gibbs free energy of the
solute in the
solvent, while
denotes the Gibbs free energy of self-solvation of the
solvent, i.e.,
, for the
solvents [
40,
52]. Likewise,
can be equivalently written in terms of the isothermal-isochoric residual chemical potential of the species,
, as follows,
where
or pure component when
, otherwise
describes the condition of infinite dilution of the
solute in an
solvent. This equation represents an alternative answer to question (
b) in the Introduction. Finally, Equation (27) can be recast in terms of the Gibbs free energy of transfer of the
solute from the
solvent to the
solvent environments according to Equations (10) and (11), i.e.,
which becomes the answer to question (a) in the Introduction as the desirable form of
.
Equations (25)–(28) reveal that the solvent effect on the Krichevskii parameter of a solute results from a linear combination of the relative solvation Gibbs free energy of the
solute in the pair of solvents. More specifically, the solvent effect on the magnitude of the Krichesvkii parameter for an
solute becomes directly proportional to the difference of two similar quantities comprising two distinctive terms, i.e., (
a) the Krichesvkii parameter for the ideal gas solute in the chosen solvents, and (
b) the ratio between the solvation Gibbs free energy of the
solute in the chosen solvents and their self-solvation counterparts. Given the relation between the solvation Gibbs free energy and the species residual free energies, Equation (27), the solvent effect on the Krichevskii parameter can be interpreted as the sum of an ideal gas contribution,
, and the difference of
prorated residual free energy ratio
for the
solvents. Moreover, because the residual quantities measure the contribution of the intermolecular interactions to the thermodynamic properties, the
prorated difference conveys the contribution of the difference of solute-solvent intermolecular interaction asymmetries to the solvent effect on the Krichevskii parameter. In fact, according to Equations (10) and (25) as well as the resulting linear behavior in
Figure 2 and
Figure 3, the solvent effect on the Krichevskii parameter of these gaseous solutes becomes also effectively linear with the difference
as illustrated in
Figure 4.
In summary, Equations (25)–(28) provide alternative direct routes to both (
a) a simple test of consistency between the calculated (by any method) Krichevskii parameters of a common
solute in the
pair of solvents through the determination of the standard Gibbs free energy for the transfer of the given
solute from the
solvent to the
solvent, and the standard thermodynamic properties of the two pure solvents, and (
b) an accurate evaluation of the effect of the solvent on the Krichevskii parameter of the
solute, i.e.,
, when we replace the
solvent with the
solvent, avoiding the regression of near-critical properties of the solute in the corresponding solvents as illustrated in
Table 4 and
Figure 4. In fact, the
values reported in
Table 4 are the outcome of the derived Equations (8), (27), and (28), which provided precisely the same answer, after invoking the properties from
Table 1 and the required thermodynamic properties of the two solvents at ambient conditions from the corresponding equations of state. Among the three theoretically equivalent expressions for
, Equations (8), (27) and (28), the first two do not require the reference Krichevskii parameter
, and thus, for practical purposes, they might be the preferred routes.
Moreover, in
Figure 4, we illustrate the comparison between the solvent
isotopic substitution effect on the Krichevskii parameter as determined by the “brute-force” subtraction approach based on the regressed coefficient
of Fernandez-Prini et al. [
24] and that from our proposed routes, including the reported uncertainties. This comparison provides clear evidence of the lack of reliability of the “brute-force” approach in the assessment of the
isotopic substituted (or for that matter, any solvent) effect from the regression of the Henry law constant and vapor–liquid distribution coefficient of solutes, as we could have anticipated given the challenges behind the measurements at near-critical compared with those at standard ambient solvent environments.
3.6. Solvent H/D−Effect on the Krichevskii Parameter of the Emblematic Ideal Gas Solute
It becomes instructive to analyze the effect of the change of solvent environment on the Krichevskii parameter for an ideal gas solute
for which we know the answer beforehand, and consequently, to be able to check the validity of the approach. From Equation (4), we obtain
so that, after introducing (29) and the condition
into Equation (10), we obtain
which is the expected answer, where we note that the critical conditions of the two solvents are obviously different.
3.7. Solvent H/D−Effect on the Krichevskii Parameter of the Emblematic Case of Lewis-Randall’s Quasi-Ideal Solutions
The mixture of water isotopomers, e.g.,
, falls into the category of quasi-ideal solutions within the Lewis-Randall reference [
53]. In fact, in their study of highly dilute aqueous solutions of heavy water, Japas et al. [
54] introduced the simplifying assumption of Raoult solution ideality to provide an estimation of the Krichevskii parameter of
in
, and arrived to the following expression in terms of the saturation pressures of the two species, (for a detailed analysis of either Lewis-Randall or Raoult solution ideality of these systems see
Appendix B)
at
and
denotes the critical temperature of the
species. Note that the Krichevskii parameter of an
solute in a
solvent is defined at the critical saturation conditions of the solvent, i.e.,
. Thus, Equation (31) becomes a good guess for the actual
given that
.
According to the description of either Hill et al. [
49] or Herrig et al. [
50] and Wagner and Pruss [
48] equations of state for heavy and light water, respectively, we have from Equation (31) that
and by the same quasi-ideal approximation for the infinitely dilute light water in heavy-water solvent we can conclude, as discussed in details in
Appendix B, that
In fact, in
Appendix B we have provided a molecular-based argument for the general scenario of a Lewis-Randall ideal solution to demonstrate rigorously that should the mixture of light and heavy water behave ideally, then
, after assuming for the sake of argument that
.
Obviously, as highlighted by Jancsó and
coll. [
53,
55], these isotopic mixtures exhibit small but non-negligible deviations from ideality, which are usually described by either the simplest symmetric
, i.e.,
, or the more realistic asymmetric
excess Gibbs free energy representation [
56]. In this context, we should note that in Table IV of Ref. [
57], the authors reported that
and
according to the behavior of
and
in the evaluation of
. While
is in agreement with the sign predicted by the non-ideal solution scenario,
is at odd. Unfortunately, the authors have not provided any information on the uncertainties for the two composition limiting derivatives involved, though we are aware of the fact that these quantities usually bear large uncertainties that would affect these outcomes [
16]. In contrast, in a later report by Bazaev et al. [
58], they determined that
and
, which are consistent with the theoretical expectations from the ideal solution approximation as discussed in
Appendix B.
4. Discussion and Relevant Observations
The proposed approach to the
effect on the Krichevskii parameter leads naturally to the assessment of this parameter for binary systems comprising isotopomers. In fact, when the
solute in solution with the original
solvent is simply another
species, i.e., the iconic special case of Lewis-Randall ideal solution, we have
,
,
, and
. Given the resulting
, from Equations (3) and (10) we have that the effect of the
solvent on the
becomes merely
, i.e.,
where the
and
species are simply two isotopomers. Therefore, depending on the solute-solvent intermolecular asymmetry and the fact that usually
at normal conditions, Equation (34) translates into two potential scenarios, either
or,
By noting that when the
species is an ideal gas,
[
30], so that for the case of mixtures of light (
species) and heavy water (
species) we have
, consequently, we expect
according to Equation (36). Otherwise, when
, we expect
according to Equation (35). In other words, Equations (35) and (36) indicate that the sign of the Krichevskii parameter of an isotopic
solute in an isotopic
solvent will be decided by either
or
conditions, where
,
, and
will be the outcome for the upper inequality, the middle equality and the lower inequality, respectively.
At this point, it is worth highlighting the subtle effect of the small perturbations of the solute-solvent intermolecular interaction asymmetry
around zero, i.e., the Lewis-Randall (Raoult) solution ideality [
59], on the non-ideality of these aqueous systems. On the one hand, the
system described as a slightly non-ideal solution characterized by the excess Gibbs free energy
with
, as suggested by Jancsó et al. [
53], leads to
after considering the definition
with
. Consequently, as the solute-solvent interaction asymmetry
vanishes, we have that
. Therefore, the reference to the Lewis-Randall (Raoult) solution ideality for the description of the behavior of the
system, i.e.,
, represents the equivalent limiting behavior,
as if the light and heavy water behaved identically, leading to
, and consequently to
, which is obviously not consistent with the actual case for the water isotopomers. In fact, the symmetric nature of the
description for the non-ideality of these mixtures is neither agreeing with the actual
evidence, nor being compatible with the general Lewis-Randall (Raoult) behavior discussed in
Appendix B which leads to
.
On the other hand, because the two water isotopomers exhibit slightly different thermodynamic behaviors, e.g.,
, we might expect a marginally asymmetric isothermal-isobaric composition representation for its excess Gibbs free energy. In other words, instead of the simple symmetric B4 form, we could have a more realistic Margules-type representation, i.e.,
[
56], so that [
60]
and consequently,
, leading to
This analysis indicates that the relative magnitude of the two activity coefficients at infinite dilution,
and
, decides the sign of the corresponding Krichevskii parameters. In fact, after invoking Equations (35) and (36), and according to the equations of state for light [
48] and heavy water [
49,
50],
, then we can reach the following conclusions,
and,
Notably, the available literature provide at least two sets of experimental data for the Krichevskii parameters
and
, i.e., those from Abdulkadirova et al. [
57] and from Bazaev et al. [
58] The first one, given in their Table IV, indicates that
, which would suggest that the two activity coefficients at infinite dilution are different and follow the relation
. In contrast, the second source indicates that
while
, resulting in two different activity coefficients at infinite dilution obeying the relation
. Therefore, while the two referred sources agreed on that
, they are at odds on the sign of
. Moreover, while the two references also agree with the outcome from the ideal solution approximation given by Japas et al. [
54], i.e.,
as in Equation (32), only does Bazaev et al. [
58] match the
counterpart.
We should emphasize that the agreement/disagreement observed in these datasets must be taken with caution given not only the approximated nature of the quasi-ideality approach and its inherent inconsistency as discussed above, but also the magnitude of the
effect relative to the size of the uncertainties in the experimentally measured coefficients associated with the calculation of the corresponding Krichevskii parameters. In fact, we should also note that the
and
are about two orders of magnitude smaller than the typical values for aqueous non-electrolyte solutes, e.g., see tabulation in Ref. [
16], making their accurate experimental determination extremely challenging.
Yet, the most important aspects of the observed disparity of results are their microscopic (solvation) interpretation and macroscopic (thermodynamic) modeling consequences. Considering its thermodynamic representation,
, and the positive definite nature of the molar volume and isothermal compressibility of the pure solvent, it becomes obvious that the sign of
is defined by the sign of the diverging partial molar volume of the solute,
, a crucial feature for the appropriate interpretation of solvation phenomena in highly compressible environments [
1,
61]. In fact, the observed solvent
effects on the Krichevskii parameter of a solute can be interpreted in terms of the solute’s ability to perturb the solvent microstructure, given that
, and the pressure perturbation
is directly linked to the structure making/breaking parameter for a general dissociative (
for non-dissociative)
solute [
62,
63], as follows
where
denotes the isothermal compressibility of the pure
solvent. Consequently, we can immediately conclude that,
The significance of Equation (44) becomes evident after noting that the sign of the pressure perturbation upon solute solvation
has been key in the characterization of the solvation behavior of solutes in near-critical solvents, so that according to Equation (43) an
solute behaves as a
structure-maker in an
solvent environment when the system exhibits a
[
62], and the solute is depicted as non-volatile [
2] or attractive [
64]. Conversely, an
solute behaves as a
structure-breaker in an
solvent environment when the system responds with a
[
62], and the solute is described as volatile [
2] or weakly attractive and repulsive [
64] in the jargon of supercritical fluid solutions [
65,
66].
More importantly, from the fundamental expression given by Equation (43), we can split
into its solvation (i.e., short-range local density perturbation,
) contribution while isolating its diverging (i.e., long-range or compressibility driven,
) contribution associated with the propagation of the density perturbation as follows [
8],
In Equation (45), we identify
as the ideal gas compressibility at the prevailing state conditions, and
as the corresponding isobaric-isothermal residual isothermal compressibility. Therefore, from Equations (43) and (45) we immediately find the desired explicit expression for the solvation finite contribution,
whose divergent compressibility-driven contribution becomes,
Moreover, as demonstrated in
Appendix C, the solvation and compressibility-driven contributions to the structure making/breaking parameter
are related as follows,
with
. Equation (48) tells us that the long-range contribution to the structure parameter of any real solute in an
solvent,
, becomes proportional to its short-range counterpart
through the negative value of the structure parameter of the ideal gas
solute in the real
solvent environment at the prevailing state conditions,
. Consequently, from Equations (44) and (A41) of the
Appendix C, we finally arrive to the following fundamental identity,
so that, the solvent effect on the Krichevskii parameter becomes,
The identity in Equation (49) emphasizes that the Krichevskii parameter of an
solute ability to perturb the
solvent environment is simply that of the corresponding ideal gas solute
prorated by
times the short range (finite) contribution to the structure making/breaking parameter at critical conditions. Any increase (decrease) in the
solute ability to perturb the
solvent environment as a structure-making effect,
, will translate into a more (less) negative
. Otherwise, any increase (decrease) in the
solute ability to perturb the
solvent as a structure-breaking effect,
, will translate into a more (less) positive
. Likewise, when the
solute is identical to the
solvent (
), the effect of the
solvent (
) will manifest as slightly positive, i.e.,
(see (A44) in
Appendix D). In other words, according to the analysis above, a
molecule as a solute will exhibit a structure-breaking behavior in the solvent
environment,
, while a
molecule as a solute will induce a structure-making perturbation of the solvent
environment,
(i.e.,
according to (A43) in
Appendix D).
5. Final Remarks and Outlook
In this work we have discussed the solvent effect on the Krichevskii parameter of an solute in a solvent, , and addressed its accurate determination when we know either (a) not only the solvation behavior of the solute in a solvent but also, its Krichevskii parameter , or (b) the solvation behavior of the solute in both solvents as well as the Gibbs free energy of transfer of the solute between the two solvents. For that purpose, we first proposed a general molecular thermodynamic approach based on a Gibbs free energy cycle at standard state conditions, and then, we applied it to the determination of the isotopic substitution effect on the Krichevskii parameter of gaseous solutes in light and heavy water.
Although theoretically equivalent, the choice among the resulting Equations (8), (27) and (29) would depend on the non-trivial condition of accuracy of the available data for the Krichevskii parameter of the solute in the reference solvent. Consequently, it becomes more fruitful to assess directly the solvent effect as , Equations (8) and (27), and after validating the accuracy of , proceed with the evaluation of .
The proposed scheme, developed around a fundamentally based solvation formalism of dilute solutions, identifies the links between the standard solvation Gibbs free energy of the solute in the two participating solvent environments and the resulting Krichevskii parameters, thorough the linear relation between the latter and the standard solvation Gibbs free energy of the solute. Additionally, it provides a novel microstructural interpretation of the solvent effect on the Krichevskii parameter through the rigorous characterization of the critical solvation as described by a finite unambiguous structure making/breaking parameter of the solute in the pair of solvent environments. The molecular thermodynamic foundations of the proposed approach, combined with the involvement of accurate standard solvation properties, provide a broader and encouraging outlook on the understanding, and consequent interpretation, of the solvent effect on the Krichevskii parameter of any solute in any solvent environment.