Pressure Ulcers and Dressings: A Strain Sensitivity Analysis of the Boundary Conditions of a Finite Element Model
Abstract
:1. Introduction
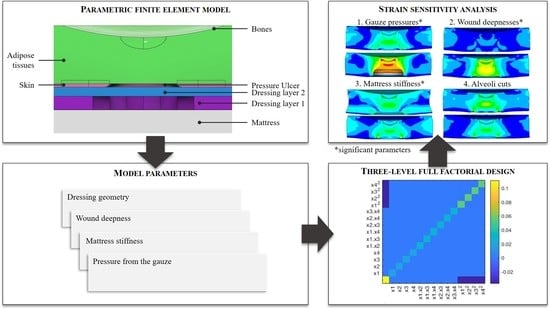
2. Materials and Methods
2.1. Reference Finite Element Model
2.2. Sensitivity Analysis
3. Results
4. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Labeau, S.O.; Afonso, E.; Benbenishty, J.; Blackwood, B.; Boulanger, C.; Brett, S.J.; Calvino-Gunther, S.; Chaboyer, W.; Coyer, F.; Deschepper, M.; et al. Prevalence, associated factors and outcomes of pressure injuries in adult intensive care unit patients: The DecubICUs study. Intensiv. Care Med. 2020, 47, 160–169. [Google Scholar] [CrossRef] [PubMed]
- Demarré, L.; Van Lancker, A.; Van Hecke, A.; Verhaeghe, S.; Grypdonck, M.; Lemey, J.; Annemans, L.; Beeckman, D. The cost of prevention and treatment of pressure ulcers: A systematic review. Int. J. Nurs. Stud. 2015, 52, 1754–1774. [Google Scholar] [CrossRef] [PubMed]
- Graves, N.; Birrell, F.; Whitby, M. Effect of Pressure Ulcers on Length of Hospital Stay. Infect. Control Hosp. Epidemiol. 2005, 26, 293–297. [Google Scholar] [CrossRef] [PubMed]
- Theisen, S.; Drabik, A.; Stock, S. Pressure ulcers in older hospitalised patients and its impact on length of stay: A retrospective observational study. J. Clin. Nurs. 2011, 21, 380–387. [Google Scholar] [CrossRef] [PubMed]
- Loerakker, S.; Stekelenburg, A.; Strijkers, G.; Rijpkema, J.J.M.; Baaijens, F.P.T.; Bader, D.L.; Nicolay, K.; Oomens, C.W.J. Temporal effects of mechanical loading on deformation-induced damage in skeletal muscle tissue. Ann. Biomed. Eng. 2010, 38, 2577–2587. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gefen, A.; Brienza, D.M.; Cuddigan, J.; Haesler, E.; Kottner, J. Our contemporary understanding of the aetiology of pressure ulcers/pressure injuries. Int. Wound J. 2021, 19, 692–704. [Google Scholar] [CrossRef]
- Ceelen, K.; Stekelenburg, A.; Loerakker, S.; Strijkers, G.; Bader, D.; Nicolay, K.; Baaijens, F.; Oomens, C. Compression-induced damage and internal tissue strains are related. J. Biomech. 2008, 41, 3399–3404. [Google Scholar] [CrossRef]
- Bouten, C.V.C.; Knight, M.M.; Lee, D.A.; Bader, D.L. Compressive deformation and damage of muscle cell subpopulations in a model system. Ann. Biomed. Eng. 2001, 29, 153–163. [Google Scholar] [CrossRef] [Green Version]
- Oomens, C.W.J.; Bressers, O.F.J.T.; Bosboom, E.M.; Bouten, C.; Bader, D.D. Can loaded interface characteristics influence strain distributions in muscle adjacent to bony prominences? Comput. Methods Biomech. Biomed. Eng. 2003, 6, 171–180. [Google Scholar] [CrossRef] [Green Version]
- Palese, A.; Saiani, L.; Pota, I.; Laquintana, D.; Stinco, G.; Di Giulio, P. What is the healing time of stage II pressure ulcers? Findings from a secondary analysis. Adv. Ski. Wound Care 2015, 28, 69–75. [Google Scholar] [CrossRef]
- Fougeron, N.; Connesson, N.; Chagnon, G.; Alonso, T.; Pasquinet, L.; Bahuon, M.; Guillin, E.; Perrier, A.; Payan, Y. New pressure ulcers dressings to alleviate human soft tissues: A finite element study. J. Tissue Viability 2022, 31, 506–513. [Google Scholar] [CrossRef]
- Ceelen, K.K.; Stekelenburg, A.; Mulders, J.L.J.; Strijkers, G.J.; Baaijens, F.P.T.; Nicolay, K.; Oomens, C.W.J. Validation of a numerical model of skeletal muscle compression with MR tagging: A contribution to pressure ulcer research. J. Biomech. Eng. 2008, 130, 061015. [Google Scholar] [CrossRef]
- Savonnet, L.; Wang, X.; Duprey, S. Finite element models of the thigh-buttock complex for assessing static sitting discomfort and pressure sore risk: A literature review. Comput. Methods Biomech. Biomed. Eng. 2018, 21, 379–388. [Google Scholar] [CrossRef] [Green Version]
- Gefen, A.; Krämer, M.; Brehm, M.; Burckardt, S. The biomechanical efficacy of a dressing with a soft cellulose fluff core in prophylactic use. Int. Wound J. 2020, 17, 1968–1985. [Google Scholar] [CrossRef]
- Linder-Ganz, E.; Gefen, A. Stress analyses coupled with damage laws to determine biomechanical risk factors for deep tissue injury during sitting. J. Biomech. Eng. 2008, 131, 011003. [Google Scholar] [CrossRef]
- Schwartz, D.; Gefen, A. The biomechanical protective effects of a treatment dressing on the soft tissues surrounding a non-offloaded sacral pressure ulcer. Int. Wound J. 2019, 16, 684–695. [Google Scholar] [CrossRef]
- Schwartz, D.; Levy, A.; Gefen, A. A Computer Modeling Study to Assess the Durability of Prophylactic Dressings Subjected to Moisture in Biomechanical Pressure Injury Prevention. Ostomy Wound Manag. 2018, 64, 18–26. [Google Scholar] [CrossRef]
- Macron, A.; Pillet, H.; Doridam, J.; Rivals, I.; Sadeghinia, M.J.; Verney, A.; Rohan, P.-Y. Is a simplified Finite Element model of the gluteus region able to capture the mechanical response of the internal soft tissues under compression? J. Tissue Viability 2019, 217, 81–90. [Google Scholar] [CrossRef] [Green Version]
- Call, E.; Pedersen, J.; Bill, B.; Black, J.; Alves, P.; Brindle, C.T.; Dealey, C.; Santamaria, N.; Clark, M. Enhancing pressure ulcer prevention using wound dressings: What are the modes of action? Int. Wound J. 2013, 12, 408–413. [Google Scholar] [CrossRef]
- Plagenhoef, S.; Evans, F.G.; Abdelnour, T. Anatomical Data for Analyzing Human Motion University of Massachusetts -Amherst. Res. Q. Exerc. Sport 1983, 54, 169–178. [Google Scholar] [CrossRef]
- Isihara, A.; Hashitsume, N.; Tatibana, M. Statistical theory of rubber-like elasticity. IV. (Two-dimensional stretching). J. Chem. Phys. 1951, 19, 1508–1512. [Google Scholar] [CrossRef]
- Annaidh, A.N.; Bruyère-Garnier, K.; Destrade, M.; Gilchrist, M.D.; Otténio, M. Characterization of the anisotropic mechanical properties of excised human skin. J. Mech. Behav. Biomed. Mater. 2012, 5, 139–148. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yeoh, O.H. Some forms of the strain energy function for rubber. Rubber Chem. Technol. 1993, 66, 754–771. [Google Scholar] [CrossRef]
- Sommer, G.; Eder, M.; Kovacs, L.; Pathak, H.; Bonitz, L.; Mueller, C.; Regitnig, P.; Holzapfel, G.A. Multiaxial mechanical properties and constitutive modeling of human adipose tissue: A basis for preoperative simulations in plastic and reconstructive surgery. Acta Biomater. 2013, 9, 9036–9048. [Google Scholar] [CrossRef]
- Mott, P.; Dorgan, J.; Roland, C. The bulk modulus and Poisson’s ratio of “incompressible” materials. J. Sound Vib. 2008, 312, 572–575. [Google Scholar] [CrossRef]
- Lee, W.; Won, B.H.; Cho, S.W. Finite element modeling for predicting the contact pressure between a foam mattress and the human body in a supine position. Comput. Methods Biomech. Biomed. Eng. 2016, 20, 104–117. [Google Scholar] [CrossRef]
- Dickinson, A.; Steer, J.; Worsley, P. Finite element analysis of the amputated lower limb: A systematic review and recommendations. Med. Eng. Phys. 2017, 43, 1–18. [Google Scholar] [CrossRef]
- Keenan, B.E.; Evans, S.L.; Oomens, C.W. A review of foot finite element modelling for pressure ulcer prevention in bedrest: Current perspectives and future recommendations. J. Tissue Viability 2021, 31, 73–83. [Google Scholar] [CrossRef]
- Bonet, J.; Wood, R.D. Nonlinear Continuum Mechanics for Finite Element Analysis, 2nd ed.; Cambridge University Press: New York, NY, USA, 2008. [Google Scholar] [CrossRef] [Green Version]
- Clark, M.; Rowland, L.; Wood, H.; Crow, R. Measurement of soft tissue thickness over the sacrum of elderly hospital patients using B-mode ultrasound. J. Biomed. Eng. 1989, 11, 200–202. [Google Scholar] [CrossRef]





| Component | C10 (MPa) | C20 (MPa) | C30 (MPa) | µ (MPa) | EX (MPa) | EY (MPa) | EZ (MPa) | d1 (MPa−1) | ν |
|---|---|---|---|---|---|---|---|---|---|
| Adipose tissue | 1.3 × 10−4 | 0.0 | 12.2 × 10−3 | - | - | - | - | 1.6 | 0.4999 |
| Skin | 2.7 × 10−1 | 1.9 | - | - | - | - | - | - | 0.4999 |
| Dressing layer 1 | - | - | - | 1.0 × 10−3 | - | - | - | - | - |
| Dressing layer 2 | - | - | - | - | 4.4 | 1.8 | 2.6 × 10−2 | - | 0.2560 |
| Mattress | - | - | - | - | 2.3 × 10−1 | - | - | - | 0.3000 |
| Parameters | Minimal Level | Intermediate Level | Maximal Level |
|---|---|---|---|
| Wound deepness | 1.30 mm | 3.20 mm | 5.00 mm |
| Alveoli cut | Recommended +1 layer | Recommended | Recommended −1 layer |
| Mattress stiffness | 0.03 MPa | 0.23 MPa | 0.43 MPa |
| Gauze pressure | 0.00 MPa | 0.02 MPa | 0.04 MPa |
| Parameters | Coefficients θi and θii or θij | Sensitivities Si or Sij (%) |
|---|---|---|
| Gauze pressure | −3.9, −10.7 | 60 |
| Wound deepness | −4.3, −3.3 | 28 |
| Wound deepness∗Gauze pressure | +4.6 | 10 |
| Mattress stiffness | +1.1, −0.9 | 1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fougeron, N.; Rivals, I.; Connesson, N.; Chagnon, G.; Alonso, T.; Pasquinet, L.; Auguste, S.; Perrier, A.; Payan, Y. Pressure Ulcers and Dressings: A Strain Sensitivity Analysis of the Boundary Conditions of a Finite Element Model. Biomechanics 2023, 3, 1-12. https://doi.org/10.3390/biomechanics3010001
Fougeron N, Rivals I, Connesson N, Chagnon G, Alonso T, Pasquinet L, Auguste S, Perrier A, Payan Y. Pressure Ulcers and Dressings: A Strain Sensitivity Analysis of the Boundary Conditions of a Finite Element Model. Biomechanics. 2023; 3(1):1-12. https://doi.org/10.3390/biomechanics3010001
Chicago/Turabian StyleFougeron, Nolwenn, Isabelle Rivals, Nathanaël Connesson, Grégory Chagnon, Thierry Alonso, Laurent Pasquinet, Stéphane Auguste, Antoine Perrier, and Yohan Payan. 2023. "Pressure Ulcers and Dressings: A Strain Sensitivity Analysis of the Boundary Conditions of a Finite Element Model" Biomechanics 3, no. 1: 1-12. https://doi.org/10.3390/biomechanics3010001