Calculating the Electrical Conductivity of Graphene Nanoplatelet Polymer Composites by a Monte Carlo Method
Abstract
:1. Introduction
2. Monte Carlo Method for Graphene Nanoplatelet Polymer Composites
2.1. The GNP Networks
2.2. Graphene Conductance, Contact Conductance and Interlayer Conductance
2.3. Potential Equations of GNPs
2.4. Potential Equations of CS
2.5. The Conductance of the Nanocomposite
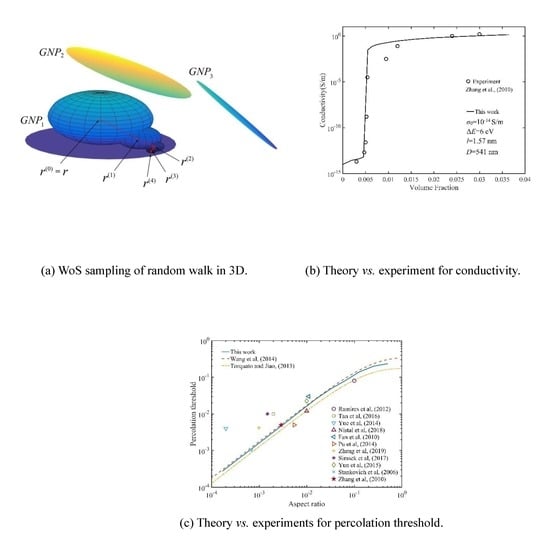
3. Results and Discussion
4. Concluding Remarks
Author Contributions
Funding
Conflicts of Interest
References
- Mogera, U.; Kulkarni, G.U. A new twist in graphene research: Twisted graphene. Carbon 2020, 156, 470–487. [Google Scholar] [CrossRef]
- Banszerus, L.; Schmitz, M.; Engels, S.; Goldsche, M.; Watanabe, K.; Taniguchi, T.; Beschoten, B. Ballistic transport exceeding 28μm in CVD grown graphene. Nano Lett. 2016, 16, 1387–1391. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Dasgupta, A.; Rajukumar, L.P.; Rotella, C.; Lei, Y.; Terrones, M. Covalent three-dimensional networks of graphene and carbon nanotubes: Synthesis and environmental applications. Nano Today 2017, 12, 116–135. [Google Scholar] [CrossRef]
- Gao, A.L.; Zhao, F.W.; Wang, F.; Zhang, G.F.; Zhao, S.; Cui, J.; Yan, Y.H. Highly conductive and light-weight acrylonitrile-butadiene-styrene copolymer/reduced graphene nanocomposites with segregated conductive structure. Compos. Part A Appl. Sci. Manuf. 2019, 112, 1–7. [Google Scholar] [CrossRef]
- Oh, H.; Kim, K.; Ryu, S.; Kim, J. Enhancement of thermal conductivity of polymethyl methacrylate-coated graphene/epoxy composites using admicellar polymerization with different ionic surfactants. Compos. Part A Appl. Sci. Manuf. 2019, 116, 206–215. [Google Scholar] [CrossRef]
- Hong, X.S.; Zheng, Y.Y.; Zhang, X.; Wu, X.Q. Preparation of graphene intercalated magnesium silicate for enhancing the thermal stability and thermal conductivity of ethylene-vinyl acetate copolymer. Polymer 2020, 193, 122332. [Google Scholar] [CrossRef]
- Peng, W.X.; Sun, K. Effects of Cu/graphene interface on the mechanical properties of multilayer Cu/graphene composites. Mech. Mater. 2020, 141, 103270. [Google Scholar] [CrossRef]
- Schueren, B.V.D.; Marouazi, H.E.; Mohanty, A.; Lévêque, P.; Sutter, C.; Romero, T.; Janowska, I. Polyvinyl alcohol-few layer graphene composite films prepared from aqueous colloids. Investigations of mechanical, conductive and gas barrier properties. Nanomaterials 2020, 10, 858. [Google Scholar] [CrossRef]
- Li, P.C.; Zhu, B.H.; Li, P.; Zhang, Z.H.; Li, L.Y.; Gu, Y.Z. A facile method to synthesize CdSe-reduced graphene oxide composite with good dispersion and high nonlinear optical properties. Nanomaterials 2019, 9, 957. [Google Scholar] [CrossRef] [Green Version]
- Liu, G.S.; Dai, S.X.; Zhu, B.H.; Li, P.; Wu, Z.K.; Gu, Y.Z. Third-order nonlinear optical properties of MoSe2/graphene composite materials. Opt. Laser Technol. 2019, 120, 105746. [Google Scholar] [CrossRef]
- Pepłowski, A.; Walter, P.A.; Janczak, D.; Górecka, Z.; Swieszkowski, W.; Jakubowska, M. Solventless conducting paste based on graphene nanoplatelets for printing of flexible, standalone routes in room temperature. Nanomaterials 2018, 8, 829. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wang, B.; Ruan, T.T.; Chen, Y.; Jin, F.; Peng, L.; Zhou, Y.; Wang, D.L.; Dou, S.X. Graphene-based composites for electrochemical energy storage. Energy Storage Mater. 2020, 24, 22–51. [Google Scholar] [CrossRef]
- Zhang, Z.Z.; Zhang, J.X.; Li, S.Y.; Liu, J.P.; Guo, Z.H. Effect of graphene liquid crystal on dielectric properties of polydimethylsiloxane nanocomposites. Compos. Part B Eng. 2019, 1761, 107338. [Google Scholar] [CrossRef]
- Wang, L.; Wu, Y.; Wang, Y.; Li, H.F.; Jiang, N.S.; Niu, K.M. Laterally compressed graphene foam/acrylonitrile butadiene styrene composites for electromagnetic interference shielding. Compos. Part A Appl. Sci. Manuf. 2020, 133, 105887. [Google Scholar] [CrossRef]
- Solis, C.G.; Enriquez, A.I.M.; Oliva, A.I.; Torre, A.R.L.; Oliva, J. Bioactivity of flexible graphene composites coated with a CaSiO3/acrylic polymer membrane. Mater. Chem. Phys. 2020, 2411, 122358. [Google Scholar] [CrossRef]
- Zhao, B.W.; Sun, T.; Zhou, X.; Liu, X.Z.; Li, X.X.; Zhou, K.; Dong, L.H.; Wei, D.P. Three-dimensional graphene composite containing graphene-SiO2 nanoballs and its potential application in stress sensors. Nanomaterials 2019, 9, 438. [Google Scholar] [CrossRef] [Green Version]
- Wang, F.; Zhao, D.S.; Zhang, L.B.; Fan, L.M.; Zhang, X.T.; Hu, S.N. Nanostructured nickel nitride with reduced graphene oxide composite bifunctional electrocatalysts for an efficient water-urea splitting. Nanomaterials 2019, 9, 1583. [Google Scholar] [CrossRef] [Green Version]
- Stankovich, S.; Dikin, D.A.; Dommett, G.H.B.; Kohlhaas, K.M.; Zimney, E.J.; Stach, E.A.; Piner, R.D.; Nguyen, S.T.; Ruoff, R.S. Graphene-based composite materials. Nature 2006, 442, 282–286. [Google Scholar] [CrossRef]
- Nistal, A.; Garcia, E.; Perez-Coll, D.; Prieto, C.; Belmonte, M.; Osendi, M.I.; Miranzo, P. Low percolation threshold in highly conducting graphene nanoplatelets/glass composite coatings. Carbon 2018, 139, 556–563. [Google Scholar] [CrossRef]
- Bruggeman, D.A.G. Effective medium approximation for nonlinear conductivity of a composite medium. Ann. Phys. 1935, 24, 636–679. [Google Scholar] [CrossRef]
- Weng, G.J. A dynamical theory for the Mori–Tanaka and Ponte Castañeda–Willis estimates. Mech. Mater. 2010, 42, 886–893. [Google Scholar] [CrossRef]
- Xia, X.D.; Wang, Y.; Zhong, Z.; Weng, G.J. A theory of electrical conductivity, dielectric constant, and electromagnetic interference shielding for lightweight graphene composite foams. J. Appl. Phys. 2016, 120, 085102. [Google Scholar] [CrossRef]
- Xia, X.D.; Hao, J.; Wang, Y.; Zhong, Z.; Weng, G.J. Theory of electrical conductivity and dielectric permittivity of highly aligned graphene-based nanocomposites. J. Phys. Condens. Matter. 2017, 29, 205702. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Shan, J.W.; Weng, G.J. Percolation threshold and electrical conductivity of graphene-based nanocomposites with filler agglomeration and interfacial tunneling. J. Appl. Phys. 2015, 118, 065101. [Google Scholar] [CrossRef]
- Hashemi, R.; Weng, G.J. A theoretical treatment of graphene nanocomposites with percolation threshold, tunneling-assisted conductivity and microcapacitor effect in AC and DC electrical settings. Carbon 2016, 96, 474–490. [Google Scholar] [CrossRef]
- Xia, X.D.; Wang, Y.; Zhong, Z.; Weng, G.J. A frequency-dependent theory of electrical conductivity and dielectric permittivity for graphene-polymer nanocomposites. Carbon 2017, 111, 221–230. [Google Scholar] [CrossRef]
- Torquato, S.; Jiao, Y. Effect of dimensionality on the percolation threshold of overlapping nonspherical hyperparticles. Phys. Rev. E 2013, 87, 022111. [Google Scholar] [CrossRef] [Green Version]
- Mathew, M.; Schilling, T.; Oettel, M. Connectivity percolation in suspensions of hard platelets. Phys. Rev. E 2012, 85, 061407. [Google Scholar] [CrossRef] [Green Version]
- Oskouyi, A.B.; Mertiny, P. Monte Carlo model for the study of percolation thresholds in composites filled with circular conductive nano-disks. Procedia Eng. 2011, 10, 403–408. [Google Scholar] [CrossRef] [Green Version]
- Wang, W.L.; Jayatissa, A.H. Computational and experimental study of electrical conductivity of graphene/poly(methyl methacrylate) nanocomposite using Monte Carlo method and percolation theory. Synthetic Met. 2015, 204, 141–147. [Google Scholar] [CrossRef]
- Zabihi, Z.; Araghi, H. Monte Carlo simulations of effective electrical conductivity of graphene/poly(methyl methacrylate) nanocomposite: Landauer-Buttiker approach. Synthetic Met. 2016, 217, 87–93. [Google Scholar] [CrossRef]
- Fang, C.; Zhang, J.J.; Chen, X.Q.; Weng, G.J. A Monte Carlo model with equipotential approximation and tunneling resistance for the electrical conductivity of carbon nanotube polymer composites. Carbon 2019, 146, 125–138. [Google Scholar] [CrossRef]
- Naeemi, A.; Meindl, J.D. Compact Physical Models for Multiwall Carbon-Nanotube Interconnects. IEEE Electr. Device Lett. 2006, 27, 338–340. [Google Scholar] [CrossRef]
- Peng, S.; Jin, Z.; Ma, P.; Zhang, D.Y.; Shi, J.Y.; Niu, J.B.; Wang, X.Y.; Wang, S.Q.; Li, M.; Liu, X.Y.; et al. The sheet resistance of graphene under contact and its effect on the derived specific contact resistivity. Carbon 2015, 82, 500–505. [Google Scholar] [CrossRef]
- Smith, J.T.; Franklin, A.D.; Farmer, D.B.; Dimitrakopoulos, C.D. Reducing Contact Resistance in Graphene Devices through Contact Area Patterning. ACS Nano 2013, 7, 3661–3667. [Google Scholar] [CrossRef]
- Venugopal, A.; Colombo, L.; Vogel, E.M. Contact resistance in few and multilayer graphene devices. Appl. Phys. Lett. 2010, 96, 013512. [Google Scholar] [CrossRef]
- Bao, W.S.; Meguid, S.A.; Zhu, Z.H.; Weng, G.J. Tunneling resistance and its effect on the electrical conductivity of carbon nanotube nanocomposites. J. Appl. Phys. 2012, 111, 093726. [Google Scholar] [CrossRef]
- Gong, S.; Zhu, Z.H.; Haddad, E.I. Modeling electrical conductivity of nanocomposites by considering carbon nanotube deformation at nanotube junctions. J. Appl. Phys. 2013, 114, 074303. [Google Scholar] [CrossRef]
- Hertel, T.; Walkup, R.E.; Avouris, P. Deformation of carbon nanotubes by surface van der Waals forces. Phys. Rev. B 1998, 58, 13870–13873. [Google Scholar] [CrossRef]
- Nirmalraj, P.N.; Lutz, T.; Kumar, S.; Duesberg, G.S.; Boland, J.J. Nanoscale Mapping of Electrical Resistivity and Connectivity in Graphene Strips and Networks. Nano Lett. 2011, 11, 16–22. [Google Scholar] [CrossRef]
- Vivo, B.D.; Lamberti, P.; Spinelli, G.; Tucci, V.; Vertuccio, L.; Vittoria, V. Simulation and experimental characterization of polymer/carbon nanotubes composites for strain sensor applications. J. Appl. Phys. 2014, 116, 054307. [Google Scholar] [CrossRef]
- Aitken, Z.H.; Huang, R. Effects of mismatch strain and substrate surface corrugation on morphology of supported monolayer graphene. J. Appl. Phys. 2010, 107, 123531. [Google Scholar] [CrossRef]
- Peng, X.H.; Tang, F.; Copple, A. Engineering the work function of armchair graphene nanoribbons using strain and functional species: A first principles study. J Phys. Condens. Matter 2012, 24, 075501. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Reynolds, J.F. A proof of the random-walk method for solving Laplace’s equation in 2-D. Math. Gaz. 1965, 49, 416–420. [Google Scholar] [CrossRef]
- Kyprianou, A.E.; Osojnik, A.; Shardlow, T. Unbiased ‘walk-on-spheres’ Monte Carlo methods for the fractional Laplacian. IMA J. Numer. Anal. 2018, 38, 1550–1578. [Google Scholar] [CrossRef]
- Zhang, H.B.; Zheng, W.G.; Yan, Q.; Yang, Y.; Wang, J.; Lu, Z.H.; Ji, G.Y.; Yu, Z.Z. Electrically conductive polyethylene terephthalate/graphene nanocomposites prepared by melt compounding. Polymer 2010, 51, 1191–1196. [Google Scholar] [CrossRef]
- Kim, S.Y.; Noh, Y.J.; Yu, J. Prediction and experimental validation of electrical percolation by applying a modifified micromechanics model considering multiple heterogeneous inclusions. Compos. Sci. Technol. 2015, 106, 156–162. [Google Scholar] [CrossRef]
- Ramirez, C.; Figueiredo, F.M.; Miranzo, P.; Poza, P.; Osendi, M.I. Graphene nanoplatelet/silicon nitride composites with high electrical conductivity. Carbon 2012, 50, 3607–3615. [Google Scholar] [CrossRef]
- Tan, Y.Q.; Luo, H.; Zhang, H.B.; Peng, S.M. Graphene nanoplatelet reinforced boron carbide composites with high electrical and thermal conductivity. J. Eur. Ceram. Soc. 2016, 36, 2679–2687. [Google Scholar] [CrossRef]
- Yue, L.; Pircheraghi, G.; Monemian, S.A.; Zloczower, I.M. Epoxy composites with carbon nanotubes and graphene nanoplatelets—Dispersion and synergy effects. Carbon 2014, 78, 268–278. [Google Scholar] [CrossRef]
- Fan, Y.C.; Wang, L.J.; Li, J.L.; Li, J.Q.; Sun, S.K.; Chen, F.; Chen, L.D.; Jiang, W. Preparation and electrical properties of graphene nanosheet/Al2O3 composites. Carbon 2010, 48, 1743–1749. [Google Scholar] [CrossRef]
- Pu, N.W.; Peng, Y.Y.; Wang, P.C.; Chen, C.Y.; Shi, J.N.; Liu, Y.M.; Ger, M.D.; Chang, C.L. Application of nitrogen-doped graphene nanosheets in electrically conductive adhesives. Carbon 2014, 67, 449–456. [Google Scholar] [CrossRef]
- Zheng, W.; Chen, W.G.; Zhao, Q.; Ren, S.X.; Fu, Y.Q. Interfacial structures and mechanisms for strengthening and enhanced conductivity of graphene/epoxy nanocomposites. Polymer 2019, 163, 171–177. [Google Scholar] [CrossRef]
- Simsek, I.N.G.; Nistal, A.; García, E.; Coll, D.P.; Miranzo, P.; Osendi, M.I. The effect of graphene nanoplatelets on the thermal and electrical properties of aluminum nitride ceramics. J. Eur. Ceram. Soc. 2017, 37, 3721–3729. [Google Scholar] [CrossRef]
- Yun, C.; Feng, Y.B.; Qiu, T.; Yang, J.; Li, X.Y.; Yua, L. Mechanical, electrical, and thermal properties of graphene nanosheet/aluminum nitride composites. Ceram. Int. 2015, 41, 8643–8649. [Google Scholar] [CrossRef]











© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fang, C.; Zhang, J.; Chen, X.; Weng, G.J. Calculating the Electrical Conductivity of Graphene Nanoplatelet Polymer Composites by a Monte Carlo Method. Nanomaterials 2020, 10, 1129. https://doi.org/10.3390/nano10061129
Fang C, Zhang J, Chen X, Weng GJ. Calculating the Electrical Conductivity of Graphene Nanoplatelet Polymer Composites by a Monte Carlo Method. Nanomaterials. 2020; 10(6):1129. https://doi.org/10.3390/nano10061129
Chicago/Turabian StyleFang, Chao, Juanjuan Zhang, Xiqu Chen, and George J. Weng. 2020. "Calculating the Electrical Conductivity of Graphene Nanoplatelet Polymer Composites by a Monte Carlo Method" Nanomaterials 10, no. 6: 1129. https://doi.org/10.3390/nano10061129